DOCSLIB.ORG

Cost-Effective Levee Design for Cases Along the Meuse River Including Uncertain- Ties in Hydraulic Loads

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cost-Effective Levee Design for Cases Along the Meuse River Including Uncertain- Ties in Hydraulic Loads Cost-effective levee design for cases along the Meuse river including uncertain- ties in hydraulic loads B. Broers Delft University of Technology . Cost-effective levee design for cases along the Meuse river including uncertainties in hydraulic loads by Ing. B. Broers in partial fulfilment of the requirements for the degree of Master of Science in Civil Engineering at the Delft University of Technology, Faculty of Civil Engineering and Geosciences to be defended publicly on January 15, 2015 Student number: 4184408 Supervisor: Prof. dr. ir. M. Kok, TU Delft - Hydraulic Engineering section Thesis committee: Dr. ir. T. Schweckendiek, TU Delft - Hydraulic Engineering section Ir. drs. J. G. Verlaan, TU Delft - Construction Management and Engineering section Ir. S.A. van Lammeren, Royal HaskoningDHV Ir. drs. E. R. Kuipers, Waterschap Peel en Maasvallei An electronic version of this thesis is available at http://repository.tudelft.nl/. Preface This MSc Thesis reflects the final part of the Master of Science degree in Hydraulic Engineering at the Civil Engineering and Geosciences Faculty of the Delft University of Technology. The research is per- formed under guidance of the Delft University of Technology in cooperation with Royal HaskoningDHV and Waterschap Peel & Maasvallei. I like to thank many people for their support and cooperation during my graduation thesis. In the first place I thank my direct supervisors: Timo Schweckendiek, Enno Kuipers and Bas van Lammeren for their helpful feedback, enthusiasm and guidance during the thesis. Many thanks to Prof. Matthijs Kok for his support and advice. My thanks to Jules Verlaan too, who helped me especially in the field of LCCA. Furthermore I would like to thank my colleges at Royal HaskoningDHV, for all their advices and feedback regarding the contents as well as the process of the graduation thesis. It was great to experience the company in where I was able to talk to hydraulic-, management-, LCCA-, and engineering- specialists. The MSc thesis topic originates from the Waterschap Peel & Maasvallei. Designing levees, operat- ing with a limited budged and dealing with all kinds of stakeholders and preferences is not an easy task. In my view, looking for opportunities and considering innovative ideas characterize the water board. One of the largest struggles during my thesis was to find an appropriate scope which includes both; the large variety in aspects the water board (and engineering agencies) faces as well as the detailed level of some aspects to form comprehensive results. Many colleges of the Water board gave me insight into their levee management difficulties, took effort to help me whenever I need and are very open for discussions. Therefore my thanks to these colleges as well. At last I would like to thank my friends, family and especially my fellow students for their encouragement, supported and help with the English language. At last I like to give some thoughts to the lately published report giving answers to data which are assumed in this report. On the 16th of September 2014 the Delta-committee presented the Delta Programme 2015. This program gives insight into the new safety philosophy. The new annual flood probability of Arcen has to be less than 1/300. The program reported an annual flood probability of 1/1.000 for the city-centre boulevard of Venlo. within this research a safety level of 1/1.250 is used for both case studies. Some results, like the most economical attractive robustness of the levee height, are strongly related to these changes. The calculated robustness is overestimated, but this does not change the basic methodology. Furthermore the discount rate will be (re)investigated according to the report. The belief exist that the 5,5% total real discount rate can be to high due to economical and political reasons (DP2015). B. Broers Delft, December 2014 iii Summary After the flood of 1993 and 1995 in the Netherlands, flood risks in Limburg became an important dis- cussion. Each flood defence system along the river Meuse needs to be provided with a safety level with an annual failure probability of 1/250. In the nearby future a new safety philosophy will be in- troduced entailing new safety norms and calculations techniques. The water board needs to construct levees including the knowledge of this new safety philosophy. Additionally the water board faces more problems like limited space or an intense infrastructure around the current levees. Uncertainties in hydraulic boundary conditions influence the levee design, too. An over- and underesti- mation of these conditions may lead to a cost-inefficient levee design. Moreover, innovative alternatives may be good alternatives. Including the uncertainties in the levee design alternative analysis can lead to a better decision process in where these innovations become more attractive. The objective of this MSc-thesis is to investigate which balance between levee investments and ro- bustness is most cost-effective during the levee design alternative analysis, specified for cases along the river Meuse in Limburg. Robustness within this balance is related to the uncertainties in future hydraulic boundary conditions. The main research question of the MSc-thesis therefore is: What are cost-effective levee designs including uncertainties in hydraulic boundary conditions? This research uses two case studies; Arcen and Venlo. The case study of Arcen is used to define, design and screen levee design alternatives. Furthermore an optimization procedure is developed with this case study. In Arcen some of the important problems are that the present levee passes through peoples back yards, it has a very high present failure probability and there is not much available space. The second case study will be used to confirm or reject the preliminary conclusion drawn in the Arcen case study. In Venlo, along the river Meuse a boulevard is present. This boulevard is partly protected by a demountable stop-log system which currently does not fulfil the present safety assessment. Fu- ture developments, preferences of other stakeholders and large service costs leading to a re-analysis of the levee design. Levee design alternatives are formed by combining a levee alignment with a green or structural design type. Secondly design criteria are formulated to create sketch designs per levee alternative. Next, these alternatives are screened with a multi-criteria analysis based on criteria like costs, constructibility and hydraulic impact. Alternatives which turn out to be most attractive of the MCA are referred to as realistic alternatives. These will be investigated further with help of LCCA. Life Cycle Cost Analysis or LCCA is a widely acknowledged technique to support the alternative analysis. One of the methods is the so called Net Present Value (NPV) calculations which include investments as well as benefits. This methods suits perfectly to investigate the robustness and the effect of hydraulic boundary condition uncertainties to the alternative analysis. The investments in LCCA includes among others: Project-, maintenance-, service- and end-of-life costs within the analysis period of a project. The benefits of a levee design can be estimated by calculating the flood risk reduction between the present and new situation. The NPV of a levee design alternative can be found by subtracting the present values of the investments from the benefits. A discount rate and economical growth rate is used to perform these calculations. The theoretical framework of LCCA as stated above is adapted to the optimization procedure. The aim of this procedure is to find the optimum levee height (ℎ) by seeking the robustness (Δℎ) argu- ment wherein the NPV-function attains its maximum value. v vi Summary Here the robustness is the levee height above the required height which is necessary to fulfil the present safety standards (annual exceedance probability of 1/250). Overtopping and overflow is within this model the only failure mechanism. Figure 1: Schematic overview of the optimization procedure. Figure 1 illustrate the optimization procedure in where the robustness (Δℎ) is varied. The hydraulic boundary condition uncertainties are included probabilistically (design water levels related with a 100 year analysis period t=T). If the robustness is large enough (ℎ ≥ ℎ) no major maintenance is neces- sary. Otherwise the levee height has to be increased (Δℎ) at 푡 = 푇. The uncertainties in hydraulic boundary conditions are calculated with a Monte-Carlo simulation. The maximum physically possible discharge of 4.600 푚/푠 of the river Meuse is included into the optimization procedure. Within this research three different hydraulic boundary condition uncertainty aspects are analysed quantitatively, and assumed to be independent: • The uncertainty in future river widening projects; • the uncertainty in statistics; • the uncertainty in forecasted climate changes. The uncertainties of all hydraulic aspects are assessed with respect to the new safety levels. For both cases, an annual failure probability of 1/1.250 is used. Berkhof et al. (2013) selected areas which can be used as possible future river widening projects. two scenarios are analysed for the river Meuse. A triangular distribution is chosen to represent the future river widening projects. A normal distribution is assumed for the uncertainties in statistics as it resembles an error in the use of various distributions as well as the differences in discharge measure methods and the extrapolation error. Rules of thumb are used to assume a uniform distribution for future water level increases in order to include uncertainties in forecasted climate change. A 95% confidential interval is chosen between the most positive and negative extreme scenario’s drawn up by the KNMI (van den Hurk et al. 2006). MSc thesis Bart Broers Summary vii A sensitivity analysis with help of a FORM-simulation shows that all three hydraulic boundary con- dition aspects contribute significant. The outcome of the optimization procedure of case study Arcen shows a large robustness of 0,6 meter for the case study Arcen for all levee design alternative.
Load more

Recommended publications
  • Enhancing the Resilience to Flooding Induced by Levee Breaches In
    Nat. Hazards Earth Syst. Sci., 20, 59–72, 2020 https://doi.org/10.5194/nhess-20-59-2020 © Author(s) 2020. This work is distributed under the Creative Commons Attribution 4.0 License. Enhancing the resilience to flooding induced by levee breaches in lowland areas: a methodology based on numerical modelling Alessia Ferrari, Susanna Dazzi, Renato Vacondio, and Paolo Mignosa Department of Engineering and Architecture, University of Parma, Parco Area delle Scienze 181/A, 43124 Parma, Italy Correspondence: Alessia Ferrari ([email protected]) Received: 18 April 2019 – Discussion started: 22 May 2019 Revised: 9 October 2019 – Accepted: 4 December 2019 – Published: 13 January 2020 Abstract. With the aim of improving resilience to flooding occurrence of extreme flood events (Alfieri et al., 2015) and and increasing preparedness to face levee-breach-induced in- the related damage (Dottori et al., 2018) in the future. undations, this paper presents a methodology for creating a Among the possible causes of flooding, levee breaching wide database of numerically simulated flooding scenarios deserves special attention. Due to the well-known “levee ef- due to embankment failures, applicable to any lowland area fect”, structural flood protection systems, such as levees, de- protected by river levees. The analysis of the detailed spa- termine an increase in flood exposure. In fact, the presence tial and temporal flood data obtained from these hypothetical of this hydraulic defence creates a feeling of safety among scenarios is expected to contribute both to the development people living in flood-prone areas, resulting in the growth of of civil protection planning and to immediate actions during settlements and in the reduction of preparedness and hence a possible future flood event (comparable to one of the avail- in the increase in vulnerability in those areas (Di Baldassarre able simulations in the database) for which real-time mod- et al., 2015).
    [Show full text]
  • Preliminary Report on the Performance of the New Orleans Levee Systems in Hurricane Katrina on August 29, 2005
    Preliminary Report on the Performance of the New Orleans Levee Systems in Hurricane Katrina on August 29, 2005 by R.B. Seed, P.G. Nicholson, R.A. Dalrymple, J. Battjes, R.G. Bea, G. Boutwell, J.D. Bray, B. D. Collins, L.F. Harder, J.R. Headland, M. Inamine, R.E. Kayen, R. Kuhr, J. M. Pestana, R. Sanders, F. Silva-Tulla, R. Storesund, S. Tanaka, J. Wartman, T. F. Wolff, L. Wooten and T. Zimmie Preliminary findings from field investigations and associated studies performed by teams from the University of California at Berkeley and the American Society of Civil Engineers, as well as a number of cooperating engineers and scientists, shortly after the hurricane. Report No. UCB/CITRIS – 05/01 November 2, 2005 New Orleans Levee Systems Hurricane Katrina August 29, 2005 This project was supported, in part, by the National Science Foundation under Grant No. CMS-0413327. Any opinions, findings, and conclusions or recommendations expressed in this report are those of the author(s) and do not necessarily reflect the views of the Foundation. This report contains the observations and findings of a joint investigation between independent teams of professional engineers with a wide array of expertise. The materials contained herein are the observations and professional opinions of these individuals, and does not necessarily reflect the opinions or endorsement of ASCE or any other group or agency, Table of Contents i November 2, 2005 New Orleans Levee Systems Hurricane Katrina August 29, 2005 Table of Contents Executive Summary ...……………………………………………………………… iv Chapter 1: Introduction and Overview 1.1 Introduction ………………………………………………………………... 1-1 1.2 Hurricane Katrina ………………………………………………………….
    [Show full text]
  • A FAILURE of INITIATIVE Final Report of the Select Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina
    A FAILURE OF INITIATIVE Final Report of the Select Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina U.S. House of Representatives 4 A FAILURE OF INITIATIVE A FAILURE OF INITIATIVE Final Report of the Select Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina Union Calendar No. 00 109th Congress Report 2nd Session 000-000 A FAILURE OF INITIATIVE Final Report of the Select Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina Report by the Select Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina Available via the World Wide Web: http://www.gpoacess.gov/congress/index.html February 15, 2006. — Committed to the Committee of the Whole House on the State of the Union and ordered to be printed U. S. GOVERNMEN T PRINTING OFFICE Keeping America Informed I www.gpo.gov WASHINGTON 2 0 0 6 23950 PDF For sale by the Superintendent of Documents, U.S. Government Printing Office Internet: bookstore.gpo.gov Phone: toll free (866) 512-1800; DC area (202) 512-1800 Fax: (202) 512-2250 Mail: Stop SSOP, Washington, DC 20402-0001 COVER PHOTO: FEMA, BACKGROUND PHOTO: NASA SELECT BIPARTISAN COMMITTEE TO INVESTIGATE THE PREPARATION FOR AND RESPONSE TO HURRICANE KATRINA TOM DAVIS, (VA) Chairman HAROLD ROGERS (KY) CHRISTOPHER SHAYS (CT) HENRY BONILLA (TX) STEVE BUYER (IN) SUE MYRICK (NC) MAC THORNBERRY (TX) KAY GRANGER (TX) CHARLES W. “CHIP” PICKERING (MS) BILL SHUSTER (PA) JEFF MILLER (FL) Members who participated at the invitation of the Select Committee CHARLIE MELANCON (LA) GENE TAYLOR (MS) WILLIAM J.
    [Show full text]
  • Engineering Evaluation of Hesco Barriers Performance at Fargo, ND 2009," May 2009 Engineering Evaluation of Hesco Barriers Performance at Fargo,ND 2009
    ENCLOSURE 2 Wenck Associates, Inc., "Engineering Evaluation of Hesco Barriers Performance at Fargo, ND 2009," May 2009 Engineering Evaluation of Hesco Barriers Performance at Fargo,ND 2009 Wenck File #2283-01 Prepared for: Hesco Bastion, LLC 47152 Conrad E. Anderson Drive Hammond, LA 70401 Prepared by: WENCK ASSOCIATES, INC. 3310 Fiechtner Drive; Suite 110 May 2009 Fargo, North Dakota (701) 297-9600 SWenck Table of Contents 1.0 INTRODUCTION ........................................................................................................... 1-1 1.1 Purpose of Evaluation......................................................................................... 1-3 1.2 Background Information ...................................................................................... 1-3 2.0 CITY OF FARGO USES OF HESCO BARRIERS ......................... 2-1 2.1 Number of Miles Used Versus Total ................................................................... 2-1 2 .2 S izes ........................................................................................................ ............. 2 -1 2.3 Installation Rates .................................................................................................. 2-1 2.4 Complicating Factors .......................................................................................... 2-1 3.0 INTERVIEWS WITH CITY AND CITY REPRESENTATIVES ............................. 3-1 3.1 Issues Raised and Areas of Concern .................................................................... 3-1 3.2 Comments
    [Show full text]
  • When the Levees Break: Relief Cuts and Flood Management in the Sacramento-San Joaquin Delta
    UC Berkeley Hydrology Title When the levees break: Relief cuts and flood management in the Sacramento-San Joaquin Delta Permalink https://escholarship.org/uc/item/4qt8v88d Authors Fransen, Lindsey Ludy, Jessica Matella, Mary Publication Date 2008-05-16 eScholarship.org Powered by the California Digital Library University of California When the levees break: Relief cuts and flood management in the Sacramento-San Joaquin Delta Hydrology for Planners LA 222 Lindsey Fransen, Jessica Ludy, and Mary Matella FINAL DRAFT May 16, 2008 Abstract The Sacramento-San Joaquin Delta is one of California’s most important geographic regions. It supports significant agricultural, urban, and ecological systems and delivers water to two-thirds of the state’s population, but faces extremely high risks of disaster. Largely below sea level and supported by 1,100 miles of aging dikes and levees, the Delta system is subject to frequent flooding. Jurisdictional and financial disincentives to better flood planning prevent coordination that might otherwise reduce both costs and damages. This study highlights one possible flood mitigation technique called a relief cut, which is an intentional break in a downslope levee to allow water that has overtopped or breached an upslope levee to drain back into the river. This flood management technique is “smart” when located in appropriate areas so that floodwaters can be managed most efficiently and safely after a levee break. We identify four key constraints and make four recommendations for flood management planning. The
    [Show full text]
  • Construction Guide V2 LR.Pdf
    1 Introduction – protect and survive 2 Basic construction guidelines 3 Design of Concertainer structures 4 Fill selection and characteristics 5 Preconfigured structures 6 Improvised structures 7 Maintenance and repair 8 Product technical information 9 Trial information 10 Packing and shipping 11 Conversion tables 12 Contacts 1 Introduction – protect and survive Introduction – protect and survive 1.01 HESCO® Concertainer® has Delivered flat-packed on standard been a key component in timber skids or pallets, units providing Force Protection since can be joined and extended the 1991 Gulf War. using the provided joining pins and filled using minimal Concertainer units are used manpower and commonly extensively in the protection of available equipment. personnel, vehicles, equipment and facilities in military, Concertainer units can be peacekeeping, humanitarian installed in various configurations and civilian operations. to provide effective and economical structures, tailored They are used by all major to the specific threat and level military organisations around of protection required. Protective the world, including the UK structures will normally be MOD and the US Military. designed to protect against ballistic penetration of direct fire It is a prefabricated, multi- projectiles, shaped charge cellular system, made of warheads and fragmentation. Alu-Zinc coated steel welded HESCO Guide Construction for Engineers mesh and lined with non-woven polypropylene geotextile. Introduction – protect and survive 1.02 Protection is afforded by the fill In constructing protective material of the structure as a structures, consideration must consequence of its mass and be given to normal structural physical properties, allied with design parameters. the proven dynamic properties of Concertainer units. The information included in this guide is given in good faith, Users must be aware that the however local conditions may protection afforded may vary affect the performance of HESCO Guide Construction for Engineers with different fill materials, and structures.
    [Show full text]
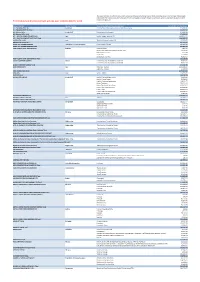
  • All Action MS502 Over USD100000
    This report provides information about FAO’s vendors and their goods and services for 2013 where the value of the Purchase Order exceeds US$100,000. This data is presented to the best of FAO's knowledge as correct. If there are omissions, errors or comments please do contact FAO Vendors with procurement actions over USD100,000 for 2013 [email protected] Name of Vendor Vendor Country General Description of Goods or Services Sum of USD Total Net Value A.G. THOMAS (PTY) LTD Swaziland Construction of Ndlolowane dam and Irrigation scheme 329,722.81 A.G. THOMAS (PTY) LTD Total 329,722.81 A.K. Bhuiyan & Co. Bangladesh Measurement instruments 172,529.31 A.K. Bhuiyan & Co. Total 172,529.31 A.T.I. SANITAL-PIEMONTE-LATECNICA Italy Facility Support Services HQ 4,490,956.25 A.T.I. SANITAL-PIEMONTE-LATECNICA Total 4,490,956.25 AASTRA ITALIA SPA Italy Technical Support Services HQ 107,679.97 AASTRA ITALIA SPA Total 107,679.97 ABDEL AAL RAGHEB COMPANY Palestinian Territory,Occupied Procurement of sheep 239,095.24 ABDEL AAL RAGHEB COMPANY Total 239,095.24 ABID HUSSAIN SHAH CORPORATION Pakistan Breeding Goats 7,865.05 Feeding Kit, Milking Kit & Milk Collection Unit 39,408.72 Milk Collection units 3,212.94 Seeds Silos 27,124.00 Seed Silos & Tool Kits 42,607.67 ABID HUSSAIN SHAH CORPORATION Total 120,218.38 ACADEV COMPANY LIMITED Ghana Constuction and rehabilitation works RAF 75,813.31 Constuction and rehabilitation works RAF 96,702.27 ACADEV COMPANY LIMITED Total 172,515.58 ACEA ENERGIA SPA Italy Electricity - Utilities 2,559,681.70 Electricity - Utilities
    [Show full text]
  • The Hurricane Katrina Levee Breach Litigation: Getting the First Geoengineering Liability Case Right
    Richards Final.docx (DO NOT DELETE) 2/10/2012 9:50 AM ESSAY THE HURRICANE KATRINA LEVEE BREACH LITIGATION: GETTING THE FIRST GEOENGINEERING LIABILITY CASE RIGHT † EDWARD P. RICHARDS INTRODUCTION In August 2005, Hurricane Katrina flattened the Gulf Coast from the Alabama border to 100 miles west of New Orleans. The New Or- leans levees failed, and much of the city was flooded. More than 1800 people died,1 and property damage is estimated at $108 billion.2 While Katrina was not the most deadly or expensive hurricane in U.S. history, it was the worst storm in more than eighty years and destroyed public complacency about the government’s ability to respond to disasters. The conventional story of the destruction of New Orleans is that the levees broke because the Army Corps of Engineers (Corps) did not design and build them correctly. The district court’s holding in In re Katrina Canal Breaches Consolidated Litigation (Robinson),3 dis- † Clarence W. Edwards Professor of Law and Director, Program in Law, Science, and Public Health at the Louisiana State University Law Center. Email: rich- [email protected]. For more information, see http://biotech.law.lsu.edu. Thanks to Kathy Haggar and Kelly Haggar of Riparian, Inc., a wetland consulting firm in Baton Rouge, Louisiana, for research assistance in geology and coastal geomorphology. 1 RICHARD D. KNABB ET AL., NAT’L HURRICANE CTR., TROPICAL CYCLONE RE- PORT: HURRICANE KATRINA 11 (2005), available at http://biotech.law.lsu.edu/ katrina/govdocs/TCR-AL122005_Katrina.pdf. 2 Id. at 13. 3 647 F. Supp.
    [Show full text]
  • A Strategic Planning Framework for Arverne East
    Planning for a Resilient Rockaways: A Strategic Planning Framework for Arverne East Waterfront Solutions (NYU): Alda Chan, Sa Liu, Jon McGrath, Rossana Tudo, Kathleen Walczak Acknowledgements This project was made possible thanks to the support of many individuals and organizations. Waterfront Solutions would like to thank everyone at Rockaway Waterfront Alliance and NYU Wagner who contributed to this endeavor. We are grateful to a number of experts and individuals who provided participated in meetings and shared information to support this report. Thanks to Arjan Braamskamp and Robert Proos (Consulate General of the Netherlands in New York), David Bragdon (NYC Department of Parks and Recreation), John Boule, (Parsons Brinkerhoff), John Young and Barry Dinerstein (NYC Department of City Planning), Jonathan Gaska (Queens Community District 14); Gerry Romski (Arverne by the Sea), Michael Polo (NYC Department of Housing Preservation and Development), Ron Schiffman (Pratt Institute); Ron Moelis and Rick Gropper (L+M Development), and Steven Bluestone (The Bluestone Organization). We would like to express our gratitude towards Robert Balder (Cornell Architecture, Art and Planning) and Walter Meyer (Local Office Landscape) for their guidance and insight during the research process. Our sincere thanks to faculty advisors Michael Keane and Claire Weisz for their feedback and support throughout this process. Front and back cover photo credit: Joe Mabel Table of Contents Executive Summary.........................................................02
    [Show full text]
  • On the Importance of Analyzing Flood Defense Failures
    7 E3S Web of Conferences, 03013 (2016) DOI: 10.1051/ e3sconf/20160703013 FLOOD risk 2016 - 3rd European Conference on Flood Risk Management On the importance of analyzing flood defense failures 2 1, Myron van Damme1,a, Timo Schweckendiek1,2 and Sebastiaan N. Jonkman1 1Delft University of Technology, Department of Hydraulic Engineering, Delft, Netherlands 2Deltares, Unit Geo-engineering, Delft, Netherlands Abstract. Flood defense failures are rare events but when they do occur lead to significant amounts of damage. The defenses are usually designed for rather low-frequency hydraulic loading and as such typically at least high enough to prevent overflow. When they fail, flood defenses like levees built with modern design codes usually either fail due to wave overtopping or geotechnical failure mechanisms such as instability or internal erosion. Subsequently geotechnical failures could trigger an overflow leading for the breach to grow in size Not only the conditions relevant for these failure mechanisms are highly uncertain, also the model uncertainty in geomechanical, internal erosion models, or breach models are high compared to other structural models. Hence, there is a need for better validation and calibration of models or, in other words, better insight in model uncertainty. As scale effects typically play an important role and full-scale testing is challenging and costly, historic flood defense failures can be used to provide insights into the real failure processes and conditions. The recently initiated SAFElevee project at Delft University of Technology aims to exploit this source of information by performing back analysis of levee failures at different level of detail. Besides detailed process based analyses, the project aims to investigate spatial and temporal patterns in deformation as a function of the hydrodynamic loading using satellite radar interferometry (i.e.
    [Show full text]
  • Restoring Gulf Oyster Reefs: Opportunities for Innovation
    RESTORING GULF OYSTER REEFS June 2012 Opportunities for Innovation Shawn Stokes Susan Wunderink Marcy Lowe Gary Gereffi Restoring Gulf Oyster Reefs This research was prepared on behalf of Environmental Defense Fund: http://www.edf.org/home.cfm Acknowledgments – The authors are grateful for valuable information and feedback from Patrick Banks, Todd Barber, Dennis Barkmeyer, Larry Beggs, Karim Belhadjali, Anne Birch, Seth Blitch, Rob Brumbaugh, Mark Bryer, Russ Burke, Rob Cook, Jeff DeQuattro, Blake Dwoskin, John Eckhoff, John Foret, Sherwood Gagliano, Kyle Graham, Timm Kroeger, Ben LeBlanc, Romuald Lipcius, John Lopez, Gus Lorber, Tom Mohrman, Tyler Ortego, Charles Peterson, George Ragazzo, Edwin Reardon, Dave Schulte, Todd Swannack, Mike Turley, and Lexia Weaver. Many thanks also to Jackie Roberts for comments on early drafts. None of the opinions or comments expressed in this study are endorsed by the companies mentioned or individuals interviewed. Errors of fact or interpretation remain exclusively with the authors. We welcome comments and suggestions. The lead author can be contacted at: [email protected] List of Abbreviations BLS Bureau of Labor and Statistics COSEE Centers for Oceans Sciences Education Excellence CWPPRA Coastal Wetlands Planning Protection and Restoration Act DEP Department of Environmental Protection DMR Mississippi Department of Marine Resources DNR Louisiana Department of Natural Resources EPA Environmental Protection Agency FWS U.S. Fish and Wildlife Service NOAA National Oceanic and Atmospheric Administration NPCA National Precast Concrete Association NRDC Natural Resources Defense Council NSF National Science Foundation OBAR Oyster Break Artificial Reef OCPR Office of Coastal Protection and Restoration SBA Small Business Association TNC The Nature Conservancy TPWD Texas Parks and Wildlife Department USACE United States Army Corps of Engineers Cover Photo: © Erika Nortemann/The Nature Conservancy.
    [Show full text]
  • Military Technology in the 12Th Century
    Zurich Model United Nations MILITARY TECHNOLOGY IN THE 12TH CENTURY The following list is a compilation of various sources and is meant as a refer- ence guide. It does not need to be read entirely before the conference. The breakdown of centralized states after the fall of the Roman empire led a number of groups in Europe turning to large-scale pillaging as their primary source of income. Most notably the Vikings and Mongols. As these groups were usually small and needed to move fast, building fortifications was the most efficient way to provide refuge and protection. Leading to virtually all large cities having city walls. The fortifications evolved over the course of the middle ages and with it, the battle techniques and technology used to defend or siege heavy forts and castles. Designers of castles focused a lot on defending entrances and protecting gates with drawbridges, portcullises and barbicans as these were the usual week spots. A detailed ref- erence guide of various technologies and strategies is compiled on the following pages. Dur- ing the third crusade and before the invention of gunpowder the advantages and the balance of power and logistics usually favoured the defender. Another major advancement and change since the Roman empire was the invention of the stirrup around 600 A.D. (although wide use is only mentioned around 900 A.D.). The stirrup enabled armoured knights to ride war horses, creating a nearly unstoppable heavy cavalry for peasant draftees and lightly armoured foot soldiers. With the increased usage of heavy cav- alry, pike infantry became essential to the medieval army.
    [Show full text]