Architecture, Size, and Reproduction in Plants: a Pollination Study Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rare Plant Survey of San Juan Public Lands, Colorado
Rare Plant Survey of San Juan Public Lands, Colorado 2005 Prepared by Colorado Natural Heritage Program 254 General Services Building Colorado State University Fort Collins CO 80523 Rare Plant Survey of San Juan Public Lands, Colorado 2005 Prepared by Peggy Lyon and Julia Hanson Colorado Natural Heritage Program 254 General Services Building Colorado State University Fort Collins CO 80523 December 2005 Cover: Imperiled (G1 and G2) plants of the San Juan Public Lands, top left to bottom right: Lesquerella pruinosa, Draba graminea, Cryptantha gypsophila, Machaeranthera coloradoensis, Astragalus naturitensis, Physaria pulvinata, Ipomopsis polyantha, Townsendia glabella, Townsendia rothrockii. Executive Summary This survey was a continuation of several years of rare plant survey on San Juan Public Lands. Funding for the project was provided by San Juan National Forest and the San Juan Resource Area of the Bureau of Land Management. Previous rare plant surveys on San Juan Public Lands by CNHP were conducted in conjunction with county wide surveys of La Plata, Archuleta, San Juan and San Miguel counties, with partial funding from Great Outdoors Colorado (GOCO); and in 2004, public lands only in Dolores and Montezuma counties, funded entirely by the San Juan Public Lands. Funding for 2005 was again provided by San Juan Public Lands. The primary emphases for field work in 2005 were: 1. revisit and update information on rare plant occurrences of agency sensitive species in the Colorado Natural Heritage Program (CNHP) database that were last observed prior to 2000, in order to have the most current information available for informing the revision of the Resource Management Plan for the San Juan Public Lands (BLM and San Juan National Forest); 2. -

Mountain Plants of Northeastern Utah
MOUNTAIN PLANTS OF NORTHEASTERN UTAH Original booklet and drawings by Berniece A. Andersen and Arthur H. Holmgren Revised May 1996 HG 506 FOREWORD In the original printing, the purpose of this manual was to serve as a guide for students, amateur botanists and anyone interested in the wildflowers of a rather limited geographic area. The intent was to depict and describe over 400 common, conspicuous or beautiful species. In this revision we have tried to maintain the intent and integrity of the original. Scientific names have been updated in accordance with changes in taxonomic thought since the time of the first printing. Some changes have been incorporated in order to make the manual more user-friendly for the beginner. The species are now organized primarily by floral color. We hope that these changes serve to enhance the enjoyment and usefulness of this long-popular manual. We would also like to thank Larry A. Rupp, Extension Horticulture Specialist, for critical review of the draft and for the cover photo. Linda Allen, Assistant Curator, Intermountain Herbarium Donna H. Falkenborg, Extension Editor Utah State University Extension is an affirmative action/equal employment opportunity employer and educational organization. We offer our programs to persons regardless of race, color, national origin, sex, religion, age or disability. Issued in furtherance of Cooperative Extension work, Acts of May 8 and June 30, 1914, in cooperation with the U.S. Department of Agriculture, Robert L. Gilliland, Vice-President and Director, Cooperative Extension -

Costs & Benefits 1 2 Title
Page 1 of 36 Ecology 1 Running Head: Mutualism exploitation: costs & benefits 2 3 Title: Costs and benefits of alternative food handling tactics help explain facultative exploitation 4 of pollination mutualisms 5 6 Elinor M. Lichtenberg1,*, Rebecca E. Irwin2,3, Judith L. Bronstein1 7 8 1) Department of Ecology & Evolutionary Biology, University of Arizona, Tucson, AZ 85721 9 USA 10 2) Department of Applied Ecology, North Carolina State University, Raleigh, NC 27695 USA 11 3) Rocky Mountain Biological Lab, Crested Butte, CO 81224 USA 12 13 Corresponding author: Elinor M. Lichtenberg, [email protected] 14 15 * Current affiliation: Department of Integrative Biology, The University of Texas at Austin, 16 Austin, TX 78712 USA 17 1 Ecology Page 2 of 36 18 Abstract 19 Many mutualisms are taken advantage of by organisms that take rewards from their partners but 20 provide no benefit in return. In the absence of traits that limit exploitation, facultative exploiters 21 (partners that can either exploit or cooperate) are widely predicted by mutualism theory to 22 choose an exploitative strategy, potentially threatening mutualism stability. However, it is 23 unknown whether facultative exploiters choose to exploit, and, if so, make this choice because it 24 is the most beneficial strategy for them. We explored these questions in a subalpine plant-insect 25 community in which individuals of several bumble bee species visit flowers both “legitimately” 26 (entering via the flower opening, picking up and depositing pollen, and hence behaving 27 mutualistically) and via nectar robbing (creating holes through corollas or using an existing hole, 28 bypassing stigmas and anthers). -

Annotated Checklist of Vascular Flora, Cedar Breaks National
National Park Service U.S. Department of the Interior Natural Resource Program Center Annotated Checklist of Vascular Flora Cedar Breaks National Monument Natural Resource Technical Report NPS/NCPN/NRTR—2009/173 ON THE COVER Peterson’s campion (Silene petersonii), Cedar Breaks National Monument, Utah. Photograph by Walter Fertig. Annotated Checklist of Vascular Flora Cedar Breaks National Monument Natural Resource Technical Report NPS/NCPN/NRTR—2009/173 Author Walter Fertig Moenave Botanical Consulting 1117 W. Grand Canyon Dr. Kanab, UT 84741 Editing and Design Alice Wondrak Biel Northern Colorado Plateau Network P.O. Box 848 Moab, UT 84532 February 2009 U.S. Department of the Interior National Park Service Natural Resource Program Center Fort Collins, Colorado The Natural Resource Publication series addresses natural resource topics that are of interest and applicability to a broad readership in the National Park Service and to others in the management of natural resources, including the scientifi c community, the public, and the NPS conservation and environmental constituencies. Manuscripts are peer-reviewed to ensure that the information is scientifi cally credible, technically accurate, appropriately written for the intended audience, and is designed and published in a professional manner. The Natural Resource Technical Report series is used to disseminate the peer-reviewed results of scientifi c studies in the physical, biological, and social sciences for both the advancement of science and the achievement of the National Park Service’s mission. The reports provide contributors with a forum for displaying comprehensive data that are often deleted from journals because of page limitations. Current examples of such reports include the results of research that addresses natural resource management issues; natural resource inventory and monitoring activities; resource assessment reports; scientifi c literature reviews; and peer- reviewed proceedings of technical workshops, conferences, or symposia. -

Washington Flora Checklist a Checklist of the Vascular Plants of Washington State Hosted by the University of Washington Herbarium
Washington Flora Checklist A checklist of the Vascular Plants of Washington State Hosted by the University of Washington Herbarium The Washington Flora Checklist aims to be a complete list of the native and naturalized vascular plants of Washington State, with current classifications, nomenclature and synonymy. The checklist currently contains 3,929 terminal taxa (species, subspecies, and varieties). Taxa included in the checklist: * Native taxa whether extant, extirpated, or extinct. * Exotic taxa that are naturalized, escaped from cultivation, or persisting wild. * Waifs (e.g., ballast plants, escaped crop plants) and other scarcely collected exotics. * Interspecific hybrids that are frequent or self-maintaining. * Some unnamed taxa in the process of being described. Family classifications follow APG IV for angiosperms, PPG I (J. Syst. Evol. 54:563?603. 2016.) for pteridophytes, and Christenhusz et al. (Phytotaxa 19:55?70. 2011.) for gymnosperms, with a few exceptions. Nomenclature and synonymy at the rank of genus and below follows the 2nd Edition of the Flora of the Pacific Northwest except where superceded by new information. Accepted names are indicated with blue font; synonyms with black font. Native species and infraspecies are marked with boldface font. Please note: This is a working checklist, continuously updated. Use it at your discretion. Created from the Washington Flora Checklist Database on September 17th, 2018 at 9:47pm PST. Available online at http://biology.burke.washington.edu/waflora/checklist.php Comments and questions should be addressed to the checklist administrators: David Giblin ([email protected]) Peter Zika ([email protected]) Suggested citation: Weinmann, F., P.F. Zika, D.E. Giblin, B. -

UC Irvine Electronic Theses and Dissertations
UC Irvine UC Irvine Electronic Theses and Dissertations Title Plant-pollinator interactions and environmental change: effects of experimental changes in phenology and water availability on a montane wildflower Permalink https://escholarship.org/uc/item/8b2263f7 Author Gallagher, Megan Katherine Publication Date 2017 License https://creativecommons.org/licenses/by/4.0/ 4.0 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA, IRVINE PLANT–POLLINATOR INTERACTIONS AND ENVIRONMENTAL CHANGE: EFFECTS OF EXPERIMENTAL CHANGES IN PHENOLOGY AND WATER AVAILABILITY ON A MONTANE WILDFLOWER DISSERTATION submitted in partial satisfaction of the requirements for the degree of DOCTOR OF PHILOSOPHY in Ecology and Evolutionary Biology by Megan Katherine Gallagher Dissertation Committee: Professor Diane R. Campbell, Chair Professor Travis E. Huxman Professor Jennifer B. H. Martiny Professor Kailen A. Mooney 2017 Chapter 1 © 2017 John Wiley and Sons, Inc. All other materials © 2017 Megan Katherine Gallagher DEDICATION “You must do something to make the world more beautiful.” ― Ms. Rumphius, by Barbara Cooney ii TABLE OF CONTENTS Page DEDICATION II LIST OF FIGURES IV LIST OF TABLES VI ACKNOWLEDGMENTS VII CURRICULUM VITAE VIII ABSTRACT OF THE DISSERTATION IX INTRODUCTION 1 Literature Cited 4 CHAPTER 1: SHIFTS IN WATER AVAILABILITY MEDIATE PLANT-POLLINATOR INTERACTIONS 7 Introduction 7 Materials and Methods 9 Results 18 Discussion 20 Literature Cited 27 CHAPTER 2: FLOWERING PHENOLOGY INFLUENCES POLLINATION BY ALTERING VISITATION RATE AND POLLINATOR EFFECTIVENESS 43 Introduction 43 Materials and methods 46 Results 59 Discussion 62 Literature Cited 70 CHAPTER 3: EXPERIMENTAL ENVIRONMENTAL CHANGE ALTERS PLANT–POLLINATOR INTERACTIONS AND SEED SET 85 Introduction 85 Methods 88 Results 96 Discussion 99 Literature Cited 106 iii LIST OF FIGURES Page Figure 1.1 Mean daily maximum soil volumetric moisture content for (a) 2013 and (b) 2014. -

(Mertensia Spp., Boraginaceae) Shang-Yao Peter Lin a Thesis
Adaptation and diversification in bluebells (Mertensia spp., Boraginaceae) Shang-Yao Peter Lin A thesis submitted in partial fulfillment of the requirements for the Doctorate in Philosophy degree in Biology Department of Biology Faculty of Science University of Ottawa © Shang-Yao Peter Lin, Ottawa, Canada, 2019 Abstract Examining the ecological processes generating evolutionary patterns is crucial to understanding how biodiversity arises and evolves. One of the most striking examples of evolutionary diversification is provided by the flowering plants (angiosperms) and their flowers. Pollinators are traditionally considered to be the most important selective agents and drivers of floral diversity. However, many angiosperms have a generalized floral morphology and are visited by a diverse and overlapping suite of pollinators, making it unclear how pollinators could have driven diversification in these taxa. In addition, flowers and plant reproductive success are likely to be influenced by factors other than pollinators, such as herbivores, precipitation, and temperature. These factors need to be considered along with pollinators in order to improve our understanding of angiosperm evolution and diversification. In my thesis, I focussed on the processes influencing adaptation and diversification in flowering plants in the genus Mertensia (Boraginaceae), which have relatively unspecialized flowers that attract a variety of nectar- and pollen-feeding insects. In Chapter One, I explored correlations among floral traits, vegetative traits, and flowering phenology across 12 Mertensia species. In Chapter Two, I assessed reproductive isolating barriers between related Mertensia species occurring in sympatry. In Chapter Three, I examined the ecological function of floral orientation in two Mertensia species with respect to pollinators and precipitation. -

1 Competition for Nectar Resources Does Not Affect Bee
Competition for nectar resources does not affect bee foraging tactic constancy Elinor M. Lichtenberg1,2,3*, Sarah K. Richman1,4*, Rebecca E. Irwin5,6, Judith L. Bronstein1 1) Department of Ecology & Evolutionary Biology, University of Arizona, Tucson, AZ 85721 USA 2) Department of Integrative Biology, The University of Texas at Austin, Austin, TX 78712 USA 3) Department of Biological Sciences and Advanced Environmental Research Institute, University of North Texas, Denton, TX 76203 USA 4) Department of Biology, University of Nevada, Reno, Reno, NV 89557 USA 5) Department of Applied Ecology, North Carolina State University, Raleigh, NC 27695 USA 6) Rocky Mountain Biological Lab, Crested Butte, CO 81224 USA *Co-first authors ORCID IDs: Elinor M. Lichtenberg, 0000-0002-2729-4534; Sarah K. Richman, 0000-0003- 1987-1140; Rebecca E. Irwin, 0000-0002-1394-4946; Judith L. Bronstein, 0000-0001-9214-1406 Running title: Nectar robbing unaffected by competition Key words: Bombus; food handling; nectar robbing; foraging; mutualism; pollination Corresponding author: Elinor M. Lichtenberg, Advanced Environmental Research Institute, University of North Texas, 1155 Union Circle #310559, Denton, TX 76203-5017, [email protected] Data Availability: The data that support the findings of this study are openly available in Zenodo at https://zenodo.org/record/3704938 (DOI: 10.5281/zenodo.3704938). 1 Abstract 1. Competition alters animal foraging, including promoting use of alternative resources. It may also impact how animals feed when they are able to handle the same food with more than one tactic. Competition likely impacts both consumers and their resources through its effects on food handling, but this topic has received little attention. -
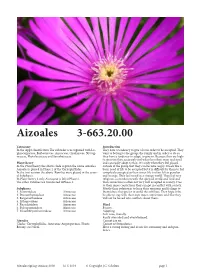
Aizoales 3-663.20.00
Aizoales 3-663.20.00 Taxonomy Introduction In the Apg2 classifcation Te suborder is recognised with Lo- Tey have a tendency to give a lot in order to be accepted. Tey phiocarpaceae, Barbeuiaceae, Aizoaceae, Gisekiaceae, Nyctag- want to belong to the group, the family and in order to do so inaceae, Phytolaccaceae and Sarcobataceae. they have a tendency to adapt, to give in. Because they are high- ly sensitive they accurately feel what the others want and need Plant theory and can easily adapt to that. It is only when they feel placed In the Plant theory the above clade is given the name Aizoales. outside of the group that they can become angry. It feels like a Aizoales is placed in Phase 2 of the Caryophyllidae. basic need of life to be accepted but it is difcult for them to feel In the frst version the above Families were placed in the sever- completely accepted as their inner life is ofen felt as peculiar al Subphases. and strange. Tey feel weird in a strange world. Tey feel very In Plant theory 2 only Aizoaceae is lef inPhase 2. religious, a connection with the spiritual world and God and Te other Families are transferred toPhase 3. that connection is ofen not very well accepted in society. Due to their inner convictions they can get in confict with society. Subphases Mostly their solution is to keep their opinions and feelings to 1. Sesuvioideae Aizoaceae themselves; they prefer to avoid the conficts. Tey hope to be 2. Drosanthemoideae Aizoaceae be able to stay with their own inner convictions and that they 3. -

Biological Evaluation for Western Bumble Bee Bombus Occidentalis (Greene, 1858)
Biological Evaluation for Western Bumble Bee Bombus occidentalis (Greene, 1858) Photo of Bombus occidentalis about to land on Camas Camassia quamash, July 30, 2013 at Butterfly Valley Botanical Area, Plumas National Forest Service by Gary Zamzow, used by permission. Written by: J. Furnish, May 2012; Updated September, 2013 Reviewed by: Stephanie Coppeto, Wildlife Biologist, LTBMU, April 2013 Adapted for: Lassen 15 Restoration Project by John Clark, Wildlife Biologist Modoc National Forest, November 2015, Revised October 2016 1 Distribution of the western bumble bee Bombus occidentalis in the PSW Region and North America Bombus occidentalis currently occurs on many national forests throughout California (Figure 1) and in all states adjacent to California (Figure 2). Historically, the species was broadly distributed across western North America along the Pacific Coast and westward from Alaska to the Colorado Rocky Mountains (Thorp and Shepard 2005, Koch et al. 2012). Historically, B. occidentalis was one of the most broadly distributed bumble bee species in North America (Cameron et al. 2011). Currently, the western bumble bee is experiencing severe declines in distribution and abundance due to a variety of factors including diseases and loss of genetic diversity (Tommasi et al. 2004, Cameron et al. 2011, Koch et al. 2012). Figure 1. Map of PSW national forests with historic (prior to 2000) vs. recent (post) collections of the western bumble bee Bombus occidentalis. There are 116 collection records for the western bumble bee Bombus occidentalis on nine national forests of the PSW Region (Hatfield 2012): Eldorado (2), Klamath (15), Lake Tahoe Basin Management Unit (7), Lassen (29), Modoc (3), Plumas (22), Shasta-Trinity (25), Six Rivers (5) and Tahoe (6). -

Sullivantia Hapemanii (Coult
Sullivantia hapemanii (Coult. & Fisher) Coult. var. hapemanii (Hapeman’s coolwort): A Technical Conservation Assessment Prepared for the USDA Forest Service, Rocky Mountain Region, Species Conservation Project March 24, 2004 Bonnie Heidel Wyoming Natural Diversity Database University of Wyoming P.O. Box 3381 Laramie, WY 82071-3381 Peer Review Administered by Center for Plant Conservation Heidel , B. (2004, March 24). Sullivantia hapemanii var. hapemanii (Coult. & Fisher) Coult. (Hapeman’s coolwort): a technical conservation assessment. [Online]. USDA Forest Service, Rocky Mountain Region. Available: http: //www.fs.fed.us/r2/projects/scp/assessments/sullivantiahapemaniivarhapemanii.pdf [date of access]. ACKNOWLEDGEMENTS Walter Fertig, previous Wyoming Natural Diversity Database (WYNDD) botanist, provided review of this document in draft form. He and Rob Thurston (WYNDD) produced the potential distribution model for Sullivantia hapemanii and provided it for use in this project (Fertig, W. and R. Thurston 2003. Modeling the Potential Distribution of BLM Sensitive and USFWS Threatened and Endangered Plant Species in Wyoming (http://uwadmnweb.uwyo.edu/ WYNDD/Reports/pdf_fertig/FinalReport_03BLMmodeling.pdf). Report prepared for the Bureau of Land Management – Wyoming State Office by WYNDD – University of Wyoming, Laramie, WY). Critical reviews and added information were later provided by Bernie Bornong (Bighorn National Forest) and Richard Birkholz (Sheridan College) from their experience with the species, and by Gary Beauvais (WYNDD) from his experience in conducting species assessments. George Jones (WYNDD) offered additional species’ insights. Scott Laursen (WYNDD) digitized populations. Beth Burkhart (USDA Forest Service) provided comments and crucial species assessment information. The information in this report draws from the specimens and collection label information resources of the Rocky Mountain Herbarium and the studies and information resources compiled and analyzed by WYNDD. -
Status Review of Three Formerly Common Species of Bumble Bee in the Subgenus Bombus
Status Review of Three Formerly Common Species of Bumble Bee in the Subgenus Bombus Bombus affinis (the rusty patched bumble bee), B. terricola (the yellowbanded bumble bee), and B. occidentalis (the western bumble bee) Photograph of Bombus affinis by Johanna James, 2008 Prepared by: Elaine Evans (The Xerces Society), Dr. Robbin Thorp (U.C. Davis), Sarina Jepsen (The Xerces Society), and Scott Hoffman Black (The Xerces Society) 1 TABLE OF CONTENTS I. Executive Summary………………………………..……………………………. 3 II. Biology, Habitat Requirements, Pollination Ecology, and Taxonomy…………. 4 A. Biology…………………………………………………………………. 4 B. Habitat requirements…………………………………………………… 6 C. Pollination Ecology…………………………………………………….. 6 D. Taxonomy……………………………………………………………… 6 III. The rusty patched bumble bee, Bombus affinis Cresson……………………….. 7 A. Species Description…………………………………………………….. 7 B. Pollination Ecology…………………………………………………….. 8 C. Population Distribution and Status…………………………………….. 9 IV. The yellowbanded bumble bee, Bombus terricola Kirby……………………… 13 A. Species Description…………………………………………………….. 13 B. Pollination Ecology…………………………………………………….. 14 C. Population Distribution and Status…………………………………….. 14 V. The western bumble bee, Bombus occidentalis Greene………………………… 17 A. Species Description…………………………………………………….. 17 B. Pollination Ecology…………………………………………………….. 18 C. Population Distribution and Status…………………………………….. 19 VI. Current and Potential Threats – Summary of Factors for Consideration……… 24 A. Spread of Diseases and Pests by Commercial Bumble Bee Producers... 24