Humanoid Vertical Jumping Based on Force Feedback and Inertial Forces Optimization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

44 Th Series of SPP (2020
KARNATAKA STATE COUNCIL FOR SCIENCE AND TECHNOLOGY Indian Institute of Science Campus, Bengaluru – 560 012 Website: http://www.kscst.iisc.ernet.in/spp.html || Email: [email protected] || Phone: 080-23341652, 23348840/48/49 44th Series of Student Project Programme: 2020-21 List of Student Project Proposals Approved for Sponsorship 1. A.C.S. COLLEGE OF ENGINEERING, BENGALURU Sl. PROJECT PROJECT TITLE BRANCH COURSE NAME OF THE NAME OF THE STUDENT(S) SANCTIONED No. REFERENCE No. GUIDE(S) AMOUNT (IN Rs.) 1. 44S_BE_1382 FACE MASK DETECTION SYSTEM FOR THE ERA OF COVID-19 USING MACHINE COMPUTER B.E. Prof. POONAM Ms. BHAVANA G 2500.00 LEARNING TECHNIQUES SCIENCE AND KUMARI Ms. CHAITANYASHREE ENGINEERING Ms. KEERTHI L N 2. 44S_BE_1385 IOT BASED UNIT FOR COPD TREATMENT BIOMEDICAL B.E. Dr. ANITHA S Ms. RASHMI S 5500.00 ENGINEERING Ms. POOJA D 3. 44S_BE_1386 PILLBOT: A NONCONTACT MEDICINE DISPENSING ROBOT FOR PATIENTS IN BIOMEDICAL B.E. Prof. NANDITHA Ms. SHEETAL RAMESH 5000.00 QUARANTINE ENGINEERING KRISHNA Ms. R NAVYA SREE Ms. RAJESHWARI SAJITH Mr. S KOSAL RAMJI 4. 44S_BE_3064 PAIN RELIEF DEVICE FOR THE TREATMENT OF MIGRAINE BIOMEDICAL B.E. Prof. HEMANTH Ms. SHREYA CHAKRAVARTHY 5000.00 ENGINEERING KUMAR G Ms. M VAGDEVI Ms. SHREE GOWRI M H Ms. SPOORTHI N K 5. 44S_BE_3066 FABRICATION OF SHEET METAL CUTTING MACHINE AND FOOT STEP POWER MECHANICAL B.E. Prof. SUNIL RAJ B A Mr. LOHITH M C 7000.00 GENERATION ENGINEERING Mr. NITISH G Mr. VINOD KUMAR K Mr. ANIL KUMAR 6. 44S_BE_4243 INTEGRATION OF BIODEGRADABLE COMPOSITES IN AIRCFART STRUCTURES AERONAUTICAL B.E. -
30 Nov Hires Report
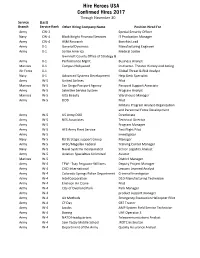
Hire Heroes USA Confirmed Hires 2017 Through November 30 Service (Last) Branch Service Rank Other Hiring Company Name Position Hired For Army CW-2 Special Security Officer Navy CW-4 Black Knight Financial Services IT Production Manager Army CW-4 ASM Research Benefits Lead Army 0-1 General Dynamics Manufacturing Engineer Army 0-1 Scribe America Medical Scribe Gwinnett County Office of Strategy & Army 0-1 Performance Mgmt. Business Analyst Marines 0-1 Campus Hollywood Instructor- Theater History and Acting Air Force 0-1 Global Threat & Risk Analyst Navy 0-1 Advanced Systems Development Help Desk Specialist Army W-5 United Airlines Pilot Marines W-5 San Diego Passport Agency Passport Support Associate Army W-5 Selective Service System Program Analyst Marines W-5 Ulta Beauty Warehouse Manager Army W-5 DOD Pilot Military Program Analyst-Organization and Personnel Force Development Army W-5 US Army DOD Directorate Army W-5 NES Associates Technical Director Army W-5 Program Manager Army W-5 AFS Army Fleet Service Test Flight Pilot Army W-5 Investigator Navy W-5 R3 Strategic support Group Manager Army W-5 AFSC/Magellan Federal Training Center Manager Navy W-5 Naval Systems Incorporated Senior Logistics Analyst Army W-5 Aviation Specialties Unlimited Aviator Marines W-5 District Manager Army W-4 TFW - Tsay Ferguson-Williams Deputy Project Manager Army W-4 CACI International Lessons Learned Analyst Army W-4 Colorado Springs Police Department Criminal Investigator Army W-4 Intel Corporation D1D Manufacturing Technician Army W-4 Erickson Air Crane -

Team Runswift University of New South Wales, Australia
Team rUNSWift University of New South Wales, Australia RoboCup 2017 Standard Platform League Gary Bai, Sean Brady, Kenji Brameld, Amri Chamela, Jeremy Collette, Samuel Collis-Bird, Kirsten Hendriks, Ethan Jones, Liangde Li, Alvin Prijatna, Peter Schmidt, Hayden Smith, Addo Wondo, Victor Wong, Maurice Pagnucco, Brad Hall, Timothy Wiley, and Claude Sammut School of Computer Science and Engineering University of New South Wales Sydney 2052 Australia http://www.cse.unsw.edu.au Abstract. RoboCup inspires and motivates our research interests in cognitive robotics and machine learning, especially vision, state-estimation, locomotion, layered hybrid architectures, and high-level programming languages. The 2017 rUNSWift team comprises final year undergradu- ate honours students, Master and PhD students, past RoboCup students and supervisors who have been involved in RoboCup for over a decade. New developments in 2017 include increased density foveation, a vision architecture change, a new ball and goal classifier, improved localising techniques, and development of both web-based and non-web based test- ing platforms. 1 The Team The RoboCup Standard Platform League (SPL) is an excellent training ground. Participant team members need to collaborate on the development of a highly complex software system, deliver it on time, and within budget. This year the UNSW SPL team comprises a mix of undergraduate, masters and PhD students, both past and present. By participating in RoboCup the team is engaged in a unique educational experience and makes a significant contribution towards research, as is evident from the list of references at the end of this article. The 2017 rUNSWift team members are Gary Bai, Sean Brady, Kenji Brameld, Amri Chamela, Samuel Collis-Bird, Kirsten Hendriks, Ethan Jones, Alvin Pri- jatna, Peter Schmidt, Hayden Smith, Liangde Li, Addo Wondo, Victor Wong, Brad Hall, Timothy Wiley, Maurice Pagnucco, and Claude Sammut. -

Malachy Eaton Evolutionary Humanoid Robotics Springerbriefs in Intelligent Systems
SPRINGER BRIEFS IN INTELLIGENT SYSTEMS ARTIFICIAL INTELLIGENCE, MULTIAGENT SYSTEMS, AND COGNITIVE ROBOTICS Malachy Eaton Evolutionary Humanoid Robotics SpringerBriefs in Intelligent Systems Artificial Intelligence, Multiagent Systems, and Cognitive Robotics Series editors Gerhard Weiss, Maastricht, The Netherlands Karl Tuyls, Liverpool, UK More information about this series at http://www.springer.com/series/11845 Malachy Eaton Evolutionary Humanoid Robotics 123 Malachy Eaton Department of Computer Science and Information Systems University of Limerick Limerick Ireland ISSN 2196-548X ISSN 2196-5498 (electronic) SpringerBriefs in Intelligent Systems ISBN 978-3-662-44598-3 ISBN 978-3-662-44599-0 (eBook) DOI 10.1007/978-3-662-44599-0 Library of Congress Control Number: 2014959413 Springer Heidelberg New York Dordrecht London © The Author(s) 2015 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. -

Challenges for Dialog in Human-Robot Interaction
Challenges for Dialog in Human-Robot Interaction Dialogs on Dialogs Meeting October 7 th 2005 Hartwig Holzapfel 1 Challenges for Dialog in Human-Robot Interaction Hartwig Holzapfel SFB 588 About me • Studied Computer Science in Karlsruhe (Germany) • Minor field of study Computational Linguistics Stuttgart (Germany) • Diploma Thesis on Emotion-Sensitive Dialogue at ISL, Prof. Waibel • Scientific employee/PhD student at Karlsruhe/Prof. Waibel since 2003 • Recent Projects – FAME: EU Project: Facilitating Agents for Multicultural Exchange presented at Barcelona Forum/ACL 2004 – SFB 588: collaborative research effort at Karlsruhe on Humanoid Robots • Research (within above projects): – Multimodal (speech+pointing synchronous and fleximodal) – Multilingual Aspects – ASR in dialogue context – Current: Cognitive Architecture for Robots and Learning 2 Challenges for Dialog in Human-Robot Interaction Hartwig Holzapfel SFB 588 Outline • Robots • SFB588: The humanoid-Robots project • The Robot „Armar“ • Interaction scenarios • Multimodal Interaction • Multilingual Speech Processing • Cognitive Architectures • Open Tasks 3 Challenges for Dialog in Human-Robot Interaction Hartwig Holzapfel SFB 588 Humanoid Robots • Why humanoid: – Humanoid body facilitates acting in a world designed for humans – Use Tools designed for humans – Interaction with humans – Intuitive multimodal communication – Other aspecs like understand human intelligence • Kind of Humanoid Robots – Service Robots – Assistants – Space – Help for elderly persons 4 Challenges for Dialog -

Improved Joint Control Using a Genetic Algorithm for a Humanoid Robot
Improved Joint Control using a Genetic Algorithm for a Humanoid Robot Jonathan Roberts1, Damien Kee2 & Gordon Wyeth2 1CSIRO Manufacturing Science & Technology PO Box 883, Kenmore, Qld 4069, Australia 2School of Information Technology & Electrical Engineering University of Queensland, St. Lucia, Qld 4072, Australia Abstract This paper describes experiments conducted in or- der to simultaneously tune 15 joints of a humanoid robot. Two Genetic Algorithm (GA) based tuning methods were developed and compared against a hand-tuned solution. The system was tuned in or- der to minimise tracking error while at the same time achieve smooth joint motion. Joint smooth- ness is crucial for the accurate calculation of on- line ZMP estimation, a prerequisite for a closed- loop dynamically stable humanoid walking gait. Results in both simulation and on a real robot are presented, demonstrating the superior smoothness performance of the GA based methods. 1 Introduction The University of Queensland GuRoo humanoid project was started in 2001 with the aim of developing a medium sized Figure 1: GuRoo. humanoid robot to be used for research. The current robot can perform a number of basic tasks, such as stand on one leg, 1.2 Future gaits (closed-loop, on-line ZMP) crouch, bow, and can also walk. Two walking gaits have been developed so far with GuRoo now able to walk unassisted. It is of course more desirable to have a closed-loop gait, where the ZMP is calculated on-line and therefore the robot is 1.1 Current gait (open-loop, off-line ZMP) capable of reacting to any external force, or instabilities (the open-loop gait is not perfect). -

Team Runswift University of New South Wales, Australia Robocup
Team rUNSWift University of New South Wales, Australia RoboCup 2014 Standard Platform League Luke Tsekouras, Jaiden Ashmore, Zijie Mei (Jacky), Belinda Teh, Oleg Sushkov, Ritwik Roy, Roger Liu, Sean Harris, Jayen Ashar, Brad Hall, Bernhard Hengst, Maurice Pagnucco, and Claude Sammut School of Computer Science and Engineering University of New South Wales Sydney 2052 Australia http://www.cse.unsw.edu.au Abstract. RoboCup inspires and motivates our research interests in cognitive robotics and machine learning, especially vision, state-estimation, locomotion, layered hybrid architectures, and high-level programming languages. The 2014 rUNSWift team comprises final year undergradu- ate honours students, Master and PhD students, past RoboCup students and supervisors who have been involved in RoboCup for over a decade. New developments in 2014 include machine learning robot recognition, improved cascading and foveation in vision to see far-away features, re- vised locomotion and kicking, shared Kalman Filter state-estimation for localisation, a coach robot, rearchitected behaviour and skills, and chal- lenge specific innovations. 1 The Team The RoboCup Standard Platform League (SPL) is an excellent training ground. Participant team members need to collaborate on the development of a highly complex software system, deliver it on time, and within budget. This year the UNSW SPL team comprises a mix of undergraduate, masters and PhD students, both past and present. Several of our team members have full-time jobs in indus- try and have come back to participate in the 2014 competition by devoting their own time and assisting a new crop of students. By participating in RoboCup the team is engaged in a unique educational experience and makes a significant contribution towards research, as is evident from the list of references at the end of this article. -

Evolution of Humanoid Robot and Contribution of Various Countries in Advancing the Research and Development of the Platform Md
International Conference on Control, Automation and Systems 2010 Oct. 27-30, 2010 in KINTEX, Gyeonggi-do, Korea Evolution of Humanoid Robot and Contribution of Various Countries in Advancing the Research and Development of the Platform Md. Akhtaruzzaman1 and A. A. Shafie2 1, 2 Department of Mechatronics Engineering, International Islamic University Malaysia, Kuala Lumpur, Malaysia. 1(Tel : +60-196192814; E-mail: [email protected]) 2 (Tel : +60-192351007; E-mail: [email protected]) Abstract: A human like autonomous robot which is capable to adapt itself with the changing of its environment and continue to reach its goal is considered as Humanoid Robot. These characteristics differs the Android from the other kind of robots. In recent years there has been much progress in the development of Humanoid and still there are a lot of scopes in this field. A number of research groups are interested in this area and trying to design and develop a various platforms of Humanoid based on mechanical and biological concept. Many researchers focus on the designing of lower torso to make the Robot navigating as like as a normal human being do. Designing the lower torso which includes west, hip, knee, ankle and toe, is the more complex and more challenging task. Upper torso design is another complex but interesting task that includes the design of arms and neck. Analysis of walking gait, optimal control of multiple motors or other actuators, controlling the Degree of Freedom (DOF), adaptability control and intelligence are also the challenging tasks to make a Humanoid to behave like a human. Basically research on this field combines a variety of disciplines which make it more thought-provoking area in Mechatronics Engineering. -

Design and Control Aspects of Humanoid Walking Robots
Lehrstuhl fur¨ Steuerungs- und Regelungstechnik Technische Universit¨at Munc¨ hen Univ.-Prof. Dr.-Ing./Univ. Tokio Martin Buss Design and Control Aspects of Humanoid Walking Robots Dirk Wollherr Vollst¨andiger Abdruck der von der Fakult¨at fur¨ Elektrotechnik und Informationstechnik der Technischen Universit¨at Munc¨ hen zur Erlangung des akademischen Grades eines Doktor-Ingenieurs (Dr.-Ing.) genehmigten Dissertation. Vorsitzender: Univ.-Prof. Dr.-Ing. Klaus Diepold Prufer¨ der Dissertation: 1. Univ.-Prof. Dr.-Ing./Univ. Tokio Martin Buss 2. Univ.-Prof. Dr.-Ing., Dr.-Ing. habil. Heinz Ulbrich Die Dissertation wurde am 31.3.2005 bei der Technischen Universit¨at Munc¨ hen eingereicht und durch die Fakult¨at fur¨ Elektrotechnik und Infromationstechnik 23.6.2005 angenommen 2 Foreword This thesis has emerged from four years of work at three different Labs. Both, the intel- lectual, and the physical journey left a significant imprint on my personality; all through the wide range of emotional experiences, ranging from the joyfull kick of success through anger and the crestfallen thought of giving up in times where nothing seems to work { in the retrospective, I do not want to miss any of it. The fundaments of this work have been laid at the Control Systems Group, Techni- sche Universit¨at Berlin, where the main task of assembling knowledge has been accom- plished and many practical experiences could be gained. With this know-how, I was given the chance to spend seven months at the Nakamura-Yamane-Lab, Department of Mechano-Informatics, University of Tokyo, where the humanoid robot UT-Theta has been developed1. This robot provided a relyable platform to experiment with walking control algorithms. -

Modeling and Control of the Anthropomimetic Robot with Antagonistic Joints in Contact and Non-Contact Tasks
UNIVERSITY OF BELGRADE SCHOOL OF ELECTRICAL ENGINEERING Kosta M. Jovanović MODELING AND CONTROL OF THE ANTHROPOMIMETIC ROBOT WITH ANTAGONISTIC JOINTS IN CONTACT AND NON-CONTACT TASKS Doctoral Dissertation Belgrade, 2015 УНИВЕРЗИТЕТ У БЕОГРАДУ ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ Коста М. Јовановић MОДЕЛИРАЊE И УПРАВЉАЊE АНТРОПОМИМЕТИЧКОГ РОБОТА СА АНТАГОНИСТИЧКИМ ПОГОНИМА У КОНТАКТНИМ И БЕСКОНТАКТНИМ ЗАДАЦИМА докторска дисертација Београд, 2015 Thesis Committee Dr. Veljko Potkonjak, Thesis Supervisor Full Professor School of Electrical Engineering, University of Belgrade, Serbia Dr. Mirjana Popović Full Professor School of Electrical Engineering, University of Belgrade, Serbia Dr. Aleksandar Rodić Scientific Advisor Mihailo Pupin Institute, University of Belgrade, Serbia Dr. Alin Albu-Schäffer Full Professor Technical University Munich, Germany; and Director of the Institute of Robotics and Mechatronics, German Aerospace Center-DLR Željko Đurović, PhD Full Professor School of Electrical Engineering, University of Belgrade, Serbia Acknowledgments A number of people have helped pave the way to my PhD. My special gratitude goes to: My wife Marija, for all the love and support, and because she learned what ZMP was when that was really important; My parents Dušica and Miloš, for their unconditional support and for making it possible for me to become professionally involved in what I love; My mentor Prof. Veljko Potkonjak, for all the opportunities he has given me, for his enormous support, and for teaching me how to become a better person and a better professional; My colleagues Bratislav, Predrag and Nenad, because our team work was extremely enjoyable; Prof. Alin Albu-Schäffer, for giving me a chance and for being my supervisor during my research stay at the DLR Institute of Robotics and Mechatronics; Prof. -

IEEE Paper Template in A4
International Journal of Advanced Technology in Engineering and Science www.ijates.com Volume No 03, Special Issue No. 01, April 2015 ISSN (online): 2348 – 7550 A CRITICAL REVIEW OF DESIGN AND TYPES OF HUMANOID ROBOT Shailendra Kumar Bohidar1, Rajni Dewangan2, Prakash Kumar Sen3 1Ph.D. Research Scholar, Kalinga University, Raipur 2Student of Mechanical Engineering, Kirodimal Institute of Technology, Raigarh (India) 3Student of M.Tech Manufacturing Management, BITS Pilani ABSTRACT This paper describes the different types of humanoid robot. The interest in assistance- and personal robots is constantly growing. Therefore robots need new, sophisticated interaction abilities. Humanlike interaction seems to be an appropriate way to increase the quality of human-robot communication. Psychologists point out that most of the human-human interaction is conducted nonverbly. The appearance demand for efficient design of humanoid robot, the mechanisms, the specifications, and many kind of humanoid robot are in also introduced. Keywords: Humanoid Robot, Human Robot Interaction, Arm, Leg I. INTRODUCTION The recent development of humanoid and interactive robots such as Honda’s [1] and Sony’s [2] is a new research direction in robotics . For many years, the human being has been trying, in all ways, to recreate the complex mechanisms that form the human body. Such task is extremely complicated and the results are not totally satisfactory. However, with increasing technological advances based on theoretical and experimental researches, man gets, in a way, to copy or to imitate some systems of the human body. These researches not only intended to create humanoid robots, great part of them constituting autonomous systems, but also, in some way, to offer a higher knowledge of the systems that form the human body, objectifying possible applications in the technology of rehabilitation of human beings, gathering in a whole studies related not only to Robotics, but also to Biomechanics, Biomimmetics, Cybernetics, among other areas. -

Runswift Walk2014 Report Robocup Standard Platform League
rUNSWift Walk2014 Report Robocup Standard Platform League Bernhard Hengst [email protected] September 30, 2014 Abstract This report describes the development and implementation of the locomotion for the Nao H25 V4 robot as used by team rUNSWift from the University of New South Wales, Australia, for the 2014 RoboCup SPL competition. We refer to the omnidirectional locomotion motion as a walk. The main purpose of the report is to document the 2014 walk for the UNSW 2014 SPL code release. School of Computer Science & Engineering University of New South Wales Sydney 2052, Australia Contents 1 Introduction 1 2 History of Walk Developments at CSE/UNSW 1 3 Background 2 3.1 Walk Basics . 2 3.2 Related Work . 3 4 Motion Architecture 5 4.1 ActionCommand . 5 4.2 Touch . 6 4.3 Generator . 6 4.4 Effector . 7 5 Walk2014Generator 7 5.1 Inverted Pendulum Dynamics . 8 5.2 Feedback Control . 10 5.3 Inverse Kinematics . 12 5.4 Stepping Through the Code . 15 5.5 Walk2014 Footstep Response to Change in Walk Parameters . 20 A Omni-directional Walking Parameterisation 23 B Kinematic Transforms for Nao Robot 23 C Kinematic Denavit-Hartenberg convention(D-H) 23 D Kinematic Chains for Nao 25 E Inverse Kinematic Matlab Code 30 i 1 Introduction This report describes the rUNSWift 2014 walk for the Nao robots used in the 2014 SPL Robocup competition in Brazil. The scope of this report is limited to describing the bipedal gait and omni-directional lo- comotion. It does not include kicking or other canned behaviour such as goalie dives and standing up after a fall.