DOCSLIB.ORG

A Literate Ray Tracer

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Literate Ray Tracer DRAFT (18 October 2001) — Do Not Distribute A LITERATE RAY TRACER Matt Pharr, Greg Humphreys, and Pat Hanrahan Copyright c 2001 Matt Pharr, Greg Humphreys, and Pat Hanrahan ii [Just as] other information should be available to those who want to learn and understand, program source code is the only means for programmers to learn the art from their predecessors. It would be unthinkable for play- wrights not to allow other playwrights to read their plays [and] only be present at theater performances where they would be barred even from taking notes. Likewise, any good author is well read, as every child who learns to write will read hundreds of times more than it writes. Program- mers, however, are expected to invent the alphabet and learn to write long novels all on their own. Programming cannot grow and learn unless the next generation of programmers have access to the knowledge and infor- mation gathered by other programmers before them. — Eric Naggum iii iv Preface This manuscript contains the documented source code for a reasonably complete ray tracing rendering system. It is written using a programming methodology called literate programming that intermingles text describing the system with the source code that implements it. This is a new approach to teaching the concepts embodied in a rendering system, from basic geometric computation to sophisticated light transport algorithms. By showing these ideas in the context of a complete and non-trivial program we also address some issues in the design and implementation of medium-sized rendering software systems. Overview and Goals lrt, the rendering system that we will describe in this book, was designed and implemented with two main goals in mind: it should be complete, and it should be illustrative. Completeness implies that the system should not lack important features found in high-end rendering systems; in particular, it means that important practical issues, such as anti-aliasing, be addressed thoroughly. It is often quite difficult to retrofit such functionality to a rendering system after it has been designed, as it can have subtle implications for all components of the system, and even the overall architectural design. In cases where lrt lacks a useful feature, we have attempted to design the architecture so that feature could be easily added without altering the overall system design. Exercises at the end of each chapter suggest programming projects that involve new features. Our second goal means that we tried to choose algorithms, data structures, and rendering techniques with care. Since their implementations will be examined by more readers than those in most rendering systems, we tried to select the best algorithms we were aware of. Clarity, simplicity, and elegance were our watchwords. Efficiency was only a tertiary goal. Since rendering systems often run for many minutes or hours in the course of generating an image, efficiency is clearly important. However, we have largely confined ourselves to v vi Preface algorithmic efficiency rather than low-level code optimization. In many cases, obvious micro-optimizations take a back seat to clear, well-organized code. For this reason as well as portability, lrt is not presented as a parallel or multi-threaded application. However, exploiting intra-frame parallelism in lrt would be straightforward in either a shared-memory or message-passing environment. In the course of presenting the implementation of lrt, we hope to convey some hard-learned lessons gleaned from experience with both commercial and academic rendering research and development. Writing a good renderer is much more complex than stringing together a set of fast algorithms; making the system robust is even harder. The system’s performance must degrade gracefully as more geometry is added to it, as more light sources are added, or as any of the other axes of complexity are pushed. Numeric stability must be handled carefully; stable algorithms that don’t waste floating-point precision are critical. A renderer is somewhat like an operating system: managing and ordering large amounts of data and computation is a critical task. RenderMan Although we won’t provide a detailed description here, lrt supports the RenderMan interface for spec- ifying scenes. RenderMan is the industry standard high quality rendering API, although the specification does not mandate the actual rendering technique to be used. Scan conversion based implementations of the RenderMan interface exist; the most notable is Pixar’s Photorealistic RenderMan, which is used for most special effects we see in movies today. Blue Moon Rendering Tools (BMRT) by Larry Gritz is a raytracing based implementation similar in spirit to lrt, but with different goals. Our ray tracer supports not only the programmatic RenderMan API, but also the Renderman Bytestream Interface (RIB). RIB is a text-file encoding of RenderMan API calls. A good introduction to the RenderMan interface is The Renderman Companion(?). Blue Moon Rendering Tools is available at http://www.bmrt.org. More information about the RIB format and detailed Renderman specifications can be found at Pixar’s web site: http://www.pixar.com. Literate Programming In the course of the development of the TEXtypesetting system, Donald Knuth developed a new program- ming methodology based on the simple idea that programs should be written more for people’s consump- tion than for computers’ consumption. He named this methodology literate programming. This manuscript (including the chapter you’re reading now) is a long literate program. Literate programs are written in a meta-language that mixes a document formatting language (e.g. LATEXand/or HTML) and a programming language (e.g. C++). The meta-language compiler then can transform the literate program into either a doc- ument suitable for typesetting (this process is generally called literate programming:weaving), or into source code suitable for compilation (literate programming:tangling). The literate programming meta-language provides two important features. The first is a set of mechanisms for mixing English text with source code. This makes the description of the program just as important as its actual source code, encouraging careful design and documentation on the part of the programmer. Second, the language provides mechanisms for presenting the program code to the reader in an entirely different order than it is supplied to the compiler. This feature makes it possible to describe the operation of the program in a very logical manner. Knuth named his literate programming system web since literate programs tend to have the form of a web: various pieces are defined and inter-related in a variety of ways and programs are written in a structure that is neither top-down nor bottom-up. As an example, consider a function InitGlobals() that is responsible for initializing all of the program’s global variables. If all of the variable initializations are presented at once, InitGlobals() may be a large collection of variable assignments whose meanings are unclear because they do not appear near the definition Literate Programming vii or use of the variables. A reader would need to search through the rest of the entire program to see where each particular variable was declared in order to understand the function and the meanings of the values it assigned to the variables. As far as the human reader is concerned, it would be better to present the initialization code near the code that actually declares the global. In a literate program, one can instead write InitGlobals like this: Function Definitions h void InitGlobals()i≡ { Initialize Global Variables } h i Here we have defined a literate progamming:fragment called Function Definitions . This fragment will be included in a source code file when the literate program is whoven for the C++ compiler;i which one isn’t important to the human reader. The fragment contains the definition of the InitGlobals function. The InitGlobals function itself includes another fragment, Initialize Global Variables . When we introduce a new global variable ErrorCount anywhere in the program,h we can now write: i Initialize Global Variables h ErrorCount = 0; i≡ Here we have started to define the contents of Initialize Global Variables . When our literate program is turned into source code suitable for compiling,h the literate programming systemi will substitute the code ErrorCount = 0; inside the definition of the InitGlobals function. Later on, we may introduce another global FragmentsProcessed, and we can append it to the fragment: Initialize Global Variables + h FragmentsProcessed =i 0;≡ The + symbol after the fragment name shows that we have added to a previously defined fragment. When woven,≡ the result of the above fragment definitions is the code: void InitGlobals() { ErrorCount = 0; FragmentsProcessed = 0; } The other main advantage of literate programming is that complex functions can be easily decomposed into logically-distinct parts. We can write a function as a series of fragments: Function Definitions + h int func(int x,i int≡ y, double *data) { int errorCount = 0; Check validity of arguments ifh (x < y) { i Swap parameter values } h i Do precomputation before loop hLoop through data array i returnh errorCount; i } viii Preface The text of each fragment is then expanded inline in func for the compiler. In the document, we can introduce each fragment and its implementation in turn–these fragments may of course include additional fragments, etc. An advantage of this style of programming is that by separating the function into logical fragments, each one can be written and verified independently–in general, we try to make each fragment less than ten lines or so of code, making it easier to understand the operation of the function as a whole. Of course, inline functions could be used similarly in a traditional programming environment, but using fragments to decompose functions has two advantages. The first is that all of the fragments can immediately refer to all of the parameters of the original function as well as any function-local variables that are declared.
Load more

Recommended publications
  • Physically Based Rendering: from Theory to Implementation Pdf, Epub, Ebook
    PHYSICALLY BASED RENDERING: FROM THEORY TO IMPLEMENTATION PDF, EPUB, EBOOK Matt Pharr, Greg Humphreys, Wenzel Jakob | 1266 pages | 18 Oct 2016 | ELSEVIER SCIENCE & TECHNOLOGY | 9780128006450 | English | San Francisco, United States Physically Based Rendering: From Theory to Implementation PDF Book The text should make more clear that we're making use of the tristimulus theory of color perception in that step. I wrote a technical perspective, The Ray-Tracing Engine That Could , that introduced the article and helped frame the work's achievements for a non-graphics audience. Design and novel uses of higher-dimensional rasterization. Lecture 7: Splines, Curves and Surfaces Shirley et al. Hardcover ISBN: Stanford csb I recently had a great time teaching the and installments of csb, the graduate-level rendering course at Stanford. A practical shading model for ray tracing. Free Shipping Free global shipping No minimum order. Then, in the code below, the negation of 'd' should be removed and in the places where 'd' is added in the computations of tx and ty, subtraction should be used. Toggle navigation pbrt. Feiner, and Kurt Akeley. Osgood this is an outstanding reference Lecture 4: Transforms Shirley et al. I was also fortunate to have the opportunity to teach the class. Given its unconventional preparation style, this textbook stands out because of its descriptions of the tradeoffs involved in developing a complete working renderer. Index of Miscellaneous Identifiers. Wenzel is also the lead developer of the Mitsuba renderer , a research-oriented rendering system. Physically Based Rendering, Second Edition , describes both the mathematical theory behind a modern photorealistic rendering system as well as its practical implementation.
    [Show full text]
  • Rendering Complex Scenes with Memory-Coherent Ray Tracing
    To appear in Proceedings of SIGGRAPH 1997 Rendering Complex Scenes with Memory-Coherent Ray Tracing Matt Pharr Craig Kolb Reid Gershbein Pat Hanrahan Computer Science Department, Stanford University Abstract both. For example, Z-buffer rendering algorithms operate on a sin- gle primitive at a time, which makes it possible to build rendering Simulating realistic lighting and rendering complex scenes are usu- hardware that does not need access to the entire scene. More re- ally considered separate problems with incompatible solutions. Ac- cently, the Talisman architecture was designed to exploit frame-to- curate lighting calculations are typically performed using ray trac- frame coherence as a means of accelerating rendering and reducing ing algorithms, which require that the entire scene database reside memory bandwidth requirements[21]. in memory to perform well. Conversely, most systems capable of Kajiya has written a whitepaper that proposes an architecture rendering complex scenes use scan-conversion algorithms that ac- for Monte Carlo ray tracing systems that is designed to improve cess memory coherently, but are unable to incorporate sophisticated coherence across all levels of the memory hierarchy, from pro- illumination. We have developed algorithms that use caching and cessor caches to disk storage[13]. The rendering computation is lazy creation of texture and geometry to manage scene complexity. decomposed into parts—ray-object intersections, shading calcula- To improve cache performance, we increase locality of reference tions, and calculating spawned rays—that are performed indepen- by dynamically reordering the rendering computation based on the dently. The coherence of memory references is increased through contents of the cache. We have used these algorithms to compute careful management of the interaction of the computation and the images of scenes containing millions of primitives, while storing memory that it references, reducing overall running time and facil- ten percent of the scene description in memory.
    [Show full text]
  • Course Overview
    Course overview Digital Image Synthesis Yung-Yu Chuang with slides by Mario Costa Sousa, Pat Hanrahan and Revi Ramamoorthi Logistics • Meeting time: 2:20pm-5:20pm, Thursday • Classroom: CSIE Room 111 • Instructor: Yung-Yu Chuang ([email protected]) • TA:陳育聖 • Webpage: http://www.csie.ntu.edu.tw/~cyy/rendering id/password • Mailing list: [email protected] Please subscribe via https://cmlmail.csie.ntu.edu.tw/mailman/listinfo/rendering/ Prerequisites • C++ programming experience is required. • Basic knowledge on algorithm and data structure is essential. • Knowledge on linear algebra, probability, calculus and numerical methods is a plus. • Though not required, it is recommended that you have background knowledge on computer graphics. Requirements (subject to change) • 3 programming assignments (60%) • Class participation (5%) • Final project (35%) Textbook Physically Based Rendering from Theory to Implementation, 2nd ed, by Matt Pharr and Greg Humphreys •Authors have a lot of experience on ray tracing •Complete (educational) code, more concrete •Has been used in many courses and papers •Implement some advanced or difficult-to-implement methods: subdivision surfaces, Metropolis sampling, BSSRDF, PRT. •3rd edition is coming next year! pbrt won Oscar 2014 •ToMatt Pharr, Greg Humphreys and Pat Hanrahan for their formalization and reference implementation of the concepts behind physically based rendering, as shared in their book Physically Based Rendering. Physically based rendering has transformed computer graphics lighting by more accurately simulating materials and lights, allowing digital artists to focus on cinematography rather than the intricacies of rendering. First published in 2004, Physically Based Rendering is both a textbook and a complete source-code implementation that has provided a widely adopted practical roadmap for most physically based shading and lighting systems used in film production.
    [Show full text]
  • An Advanced Path Tracing Architecture for Movie Rendering
    RenderMan: An Advanced Path Tracing Architecture for Movie Rendering PER CHRISTENSEN, JULIAN FONG, JONATHAN SHADE, WAYNE WOOTEN, BRENDEN SCHUBERT, ANDREW KENSLER, STEPHEN FRIEDMAN, CHARLIE KILPATRICK, CLIFF RAMSHAW, MARC BAN- NISTER, BRENTON RAYNER, JONATHAN BROUILLAT, and MAX LIANI, Pixar Animation Studios Fig. 1. Path-traced images rendered with RenderMan: Dory and Hank from Finding Dory (© 2016 Disney•Pixar). McQueen’s crash in Cars 3 (© 2017 Disney•Pixar). Shere Khan from Disney’s The Jungle Book (© 2016 Disney). A destroyer and the Death Star from Lucasfilm’s Rogue One: A Star Wars Story (© & ™ 2016 Lucasfilm Ltd. All rights reserved. Used under authorization.) Pixar’s RenderMan renderer is used to render all of Pixar’s films, and by many 1 INTRODUCTION film studios to render visual effects for live-action movies. RenderMan started Pixar’s movies and short films are all rendered with RenderMan. as a scanline renderer based on the Reyes algorithm, and was extended over The first computer-generated (CG) animated feature film, Toy Story, the years with ray tracing and several global illumination algorithms. was rendered with an early version of RenderMan in 1995. The most This paper describes the modern version of RenderMan, a new architec- ture for an extensible and programmable path tracer with many features recent Pixar movies – Finding Dory, Cars 3, and Coco – were rendered that are essential to handle the fiercely complex scenes in movie production. using RenderMan’s modern path tracing architecture. The two left Users can write their own materials using a bxdf interface, and their own images in Figure 1 show high-quality rendering of two challenging light transport algorithms using an integrator interface – or they can use the CG movie scenes with many bounces of specular reflections and materials and light transport algorithms provided with RenderMan.
    [Show full text]
  • (Gpus) for Department of Defense (Dod) Digital Signal Processing (DSP) Applications
    Assessment of Graphic Processing Units (GPUs) for Department of Defense (DoD) Digital Signal Processing (DSP) Applications John D. Owens, Shubhabrata Sengupta, and Daniel Horn† University of California, Davis † Stanford University Abstract In this report we analyze the performance of the fast Fourier transform (FFT) on graphics hardware (the GPU), comparing it to the best-of-class CPU implementation FFTW.WedescribetheFFT,thearchitectureoftheGPU,andhowgeneral-purpose computation is structured on the GPU. We then identify the factors that influence FFT performance and describe several experiments that compare these factors between the CPUandtheGPU.Weconcludethattheoverheadoftransferringdataandinitiating GPU computation are substantially higher than on the CPU, and thus for latency- critical applications, the CPU is a superior choice. We show that the CPU imple- mentation is limited by computation and the GPU implementation by GPU memory bandwidth and its lack of a writable cache. The GPU is comparatively better suited for larger FFTs with many FFTs computed in parallel in applications where FFT through- putismostimportant;ontheseapplicationsGPUandCPUperformanceisroughly on par. We also demonstrate that adding additional computation to an application that includes the FFT, particularly computation that is GPU-friendly, puts the GPU at an advantage compared to the CPU. The future of desktop processing is parallel.Thelastfewyearshaveseenanexplosionof single-chip commodity parallel architectures that promises to be the centerpieces of future computing platforms. Parallel hardware on the desktop—new multicore microprocessors, graphics processors, and stream processors—has the potential to greatly increase the com- putational power available to today’s computer users, with a resulting impact in computa- tion domains such as multimedia, entertainment, signal and image processing, and scientific computation.
    [Show full text]
  • Physically-Based Rendering Uses Physics to Simulate the Interaction Between Matter and Light, Realism Is the Primary Goal
    Logistics • Meeting time: 2:20pm-5:20pm, Thursday • Classroom: CSIE Room 111 • Instructor: Yung-Yu Chuang ([email protected]) Course overview • TA:賴威昇 • Webpage: http://www.csie.ntu.edu.tw/~cyy/rendering id/password Digital Image Synthesis • Mailing list: [email protected] Yung-Yu Chuang Please subscribe via https://cmlmail.csie.ntu.edu.tw/mailman/listinfo/rendering/ with slides by Mario Costa Sousa, Pat Hanrahan and Revi Ramamoorthi Prerequisites Requirements (subject to change) • C++ programming experience is required. • 3 programming assignments (60%) • Basic knowledge on algorithm and data • Class participation (5%) structure is essential. • Final project (35%) • Knowledge on linear algebra, probability, calculus and numerical methods is a plus. • Though not required, it is recommended that you have background knowledge on computer graphics. Textbook pbrt won Oscar 2014 Physically Based Rendering from Theory to Implementation, •ToMatt Pharr, Greg Humphreys and Pat 2nd ed, by Matt Pharr and Greg Humphreys Hanrahan for their formalization and reference •Authors have a lot of implementation of the concepts behind experience on ray tracing physically based rendering, as shared in their •Complete (educational) code, book Physically Based Rendering. more concrete Physically based rendering has •Has been used in many courses transformed computer graphics lighting by more accurately simulating materials and and papers lights, allowing digital artists to focus on •Implement some advanced or cinematography rather than the intricacies of rendering. First published in difficult-to-implement methods: 2004, Physically Based Rendering is both subdivision surfaces, Metropolis a textbook and a complete source-code sampling, BSSRDF, PRT. implementation that has provided a widely adopted practical roadmap for most •3rd edition is coming next year! physically based shading and lighting systems used in film production.
    [Show full text]
  • 01 the Implementation of a Scalable Texture Cache
    01 THE IMPLEMENTATION OF A SCALABLE TEXTURE CACHE Matt Pharr 5 March 2017 Abstract Texture caching—loading rectangular tiles of texture maps on demand and keeping a fixed number of them cached in memory—has proven to be an effective approach for limiting memory use when rendering complex scenes; scenes with gigabytes of texture can often be rendered with just tens or hundreds of megabytes of texture resident in memory. However, implementing an efficient texture cache is challenging in the presence of tens of rendering threads; each traced ray generally performs multiple cache lookups, one for each texel accessed during texture filtering, all while new tiles are being added to the cache and old tiles are recycled. Traditional thread synchronization approaches based on mutexes give poor parallel scalability with this workload. We present a texture cache implementation based on lock-free algorithms and the “read-copy update” technique, and show that it scales linearly up to (at least) 32 threads. Our implementation performs just as well as pbrt does with preloaded textures where there are no such cache maintenance complexities. Note: This document describes new functionality that may be included in a future version of pbrt. The implementation is available in the texcache branch in the pbrt-v3 repository on github. We’re interested in feedback (especially bug reports) about our implementation; please send a note to [email protected] or post to the pbrt Google Groups list if you have comments or questions. (Given that the implementation does some fairly tricky things to minimize locking and inter-thread coordination, it is entirely possible that subtle bugs remain.) 1.1 INTRODUCTION Most visually complex computer graphics scenes make extensive use of tex- ture maps to represent variation in surface appearance.
    [Show full text]
  • Generation of Points That Satisfy Two-Dimensional Elementary Intervals
    Journal of Computer Graphics Techniques Vol. 8, No. 1, 2019 http://jcgt.org Efficient Generation of Points that Satisfy Two-Dimensional Elementary Intervals Matt Pharr NVIDIA Research Figure 1. 4,096 pmj02bn samples generated using our technique. These points are progres- sive, satisfy all applicable power-of-two elementary intervals, and have optimized spectral properties. They were generated in 5.19 ms on a single core of a 4 GHz CPU. Abstract Precomputing high-quality sample points has been shown to be a useful technique for Monte Carlo integration in rendering; doing so allows optimizing properties of the points without the performance constraints of generating samples during rendering. A particularly useful property to incorporate is stratification across elementary intervals, which has been shown to reduce error in Monte Carlo integration. This is a key property of the recently-introduced progressive multi-jittered, pmj02 and pmj02bn points [Christensen et al. 2018]. For generating such sets of sample points, it is important to be able to efficiently choose new samples that are not in elementary intervals occupied by existing samples. Random search, while easy to implement, quickly becomes infeasible after a few thousand points. We describe an algorithm that efficiently generates 2D sample points that are stratified with respect to sets of elementary intervals. If a total of n sample points are being generated, then p for each sample, our algorithm uses O( n) time to build a data structure that represents the regions where a next sample may be placed. Given this data structure, valid samples can be generated in O(1) time.
    [Show full text]
  • The Path to Path-Traced Movies
    Full text available at: http://dx.doi.org/10.1561/0600000073 The Path to Path-Traced Movies Per H. Christensen Pixar Animation Studios [email protected] Wojciech Jarosz Dartmouth College [email protected] Boston — Delft Full text available at: http://dx.doi.org/10.1561/0600000073 Foundations and Trends R in Computer Graphics and Vision Published, sold and distributed by: now Publishers Inc. PO Box 1024 Hanover, MA 02339 United States Tel. +1-781-985-4510 www.nowpublishers.com [email protected] Outside North America: now Publishers Inc. PO Box 179 2600 AD Delft The Netherlands Tel. +31-6-51115274 The preferred citation for this publication is P. H. Christensen and W. Jarosz. The Path to Path-Traced Movies. Foundations and Trends R in Computer Graphics and Vision, vol. 10, no. 2, pp. 103–175, 2014. R This Foundations and Trends issue was typeset in LATEX using a class file designed by Neal Parikh. Printed on acid-free paper. ISBN: 978-1-68083-211-2 c 2016 P. H. Christensen and W. Jarosz All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, mechanical, photocopying, recording or otherwise, without prior written permission of the publishers. Photocopying. In the USA: This journal is registered at the Copyright Clearance Cen- ter, Inc., 222 Rosewood Drive, Danvers, MA 01923. Authorization to photocopy items for internal or personal use, or the internal or personal use of specific clients, is granted by now Publishers Inc for users registered with the Copyright Clearance Center (CCC).
    [Show full text]
  • Advanced Renderman 3: Render Harder
    Advanced RenderMan 3: Render Harder SIGGRAPH 2001 Course 48 course organizer: Larry Gritz, Exluna, Inc. Lecturers: Tony Apodaca, Pixar Animation Studios Larry Gritz, Exluna, Inc. Matt Pharr, Exluna, Inc. Christophe Hery, Industrial Light + Magic Kevin Bjorke, Square USA Lawrence Treweek, Sony Pictures Imageworks August 2001 ii iii Desired Background This course is for graphics programmers and technical directors. Thorough knowledge of 3D image synthesis, computer graphics illumination models and previous experience with the RenderMan Shading Language is a must. Students must be facile in C. The course is not for those with weak stomachs for examining code. Suggested Reading Material The RenderMan Companion: A Programmer’s Guide to Realistic Computer Graphics, Steve Upstill, Addison-Wesley, 1990, ISBN 0-201-50868-0. This is the basic textbook for RenderMan, and should have been read and understood by anyone attending this course. Answers to all of the typical, and many of the extremely advanced, questions about RenderMan are found within its pages. Its failings are that it does not cover RIB, only the C interface, and also that it only covers the 10-year- old RenderMan Interface 3.1, with no mention of all the changes to the standard and to the products over the past several years. Nonetheless, it still contains a wealth of information not found anyplace else. Advanced RenderMan: Creating CGI for Motion Pictures, Anthony A. Apodaca and Larry Gritz, Morgan-Kaufmann, 1999, ISBN 1-55860-618-1. A comprehensive, up-to-date, and advanced treatment of all things RenderMan. This book covers everything from basic RIB syntax to the geometric primitives to advanced topics like shader antialiasing and volumetric effects.
    [Show full text]
  • Ray Casting (Appel, 1968) Ray Casting (Appel, 1968) Ray Casting (Appel, 1968) Ray Casting (Appel, 1968)
    Logistics • Meeting time: 2:20pm-5:20pm, Thursday • Classroom: CSIE Room 111 • Instructor: Yung-Yu Chuang ([email protected]) Course overview • TA:陳育聖 • Webpage: http://www.csie.ntu.edu.tw/~cyy/rendering id/password Digital Image Synthesis • Mailing list: [email protected] Yung-Yu Chuang Please subscribe via https://cmlmail.csie.ntu.edu.tw/mailman/listinfo/rendering/ with slides by Mario Costa Sousa, Pat Hanrahan and Revi Ramamoorthi Prerequisites Requirements (subject to change) • C++ programming experience is required. • 3 programming assignments (60%) • Basic knowledge on algorithm and data • Class participation (5%) structure is essential. • Final project (35%) • Knowledge on linear algebra, probability, calculus and numerical methods is a plus. • Though not required, it is recommended that you have background knowledge on computer graphics. Textbook pbrt won Oscar 2014 Physically Based Rendering from Theory to Implementation, •ToMatt Pharr, Greg Humphreys and Pat 2nd ed, by Matt Pharr and Greg Humphreys Hanrahan for their formalization and reference •Authors have a lot of implementation of the concepts behind experience on ray tracing physically based rendering, as shared in their •Complete (educational) code, book Physically Based Rendering. more concrete Physically based rendering has •Has been used in many courses transformed computer graphics lighting by more accurately simulating materials and and papers lights, allowing digital artists to focus on •Implement some advanced or cinematography rather than the intricacies of rendering. First published in difficult-to-implement methods: 2004, Physically Based Rendering is both subdivision surfaces, Metropolis a textbook and a complete source-code sampling, BSSRDF, PRT. implementation that has provided a widely adopted practical roadmap for most •3rd edition is coming next year! physically based shading and lighting systems used in film production.
    [Show full text]
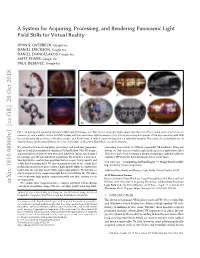
  • A System for Acquiring, Processing, and Rendering Panoramic Light Field Stills for Virtual Reality
    A System for Acquiring, Processing, and Rendering Panoramic Light Field Stills for Virtual Reality RYAN S. OVERBECK, Google Inc. DANIEL ERICKSON, Google Inc. DANIEL EVANGELAKOS, Google Inc. MATT PHARR, Google Inc. PAUL DEBEVEC, Google Inc. (a) (b) (e) (f) (g) (c) (d) (h) (i) (j) Fig. 1. Acquiring and rendering panoramic light field still images. (a,c) Our two rotating light field camera rigs: the 16×GoPro rotating array of action sports cameras (a), and a multi-rotation 2×DSLR system with two mirrorless digital cameras (c). (b,d) Long exposure photographs of the rigs operating with LED traces indicating the positions of the photographs. (e-j) Novel views of several scenes rendered by our light field renderer. The scenes are: (e) Living Room, (f) Gamble House, (g) Discovery Exterior, (h) Cheri & Gonzalo, (i) Discovery Flight Deck, and (j) St. Stephens. We present a system for acquiring, processing, and rendering panoramic generating stereo views at 90Hz on commodity VR hardware. Using our light field still photography for display in Virtual Reality (VR). We acquire system, we built a freely available light field experience application called spherical light field datasets with two novel light field camera rigs designed Welcome to Light Fields featuring a library of panoramic light field stills for for portable and efficient light field acquisition. We introduce a novel real- consumer VR which has been downloaded over 15,000 times. time light field reconstruction algorithm that uses a per-view geometry and CCS Concepts: • Computing methodologies → Image-based render- a disk-based blending field. We also demonstrate how to use a light field ing; Rendering; Image compression; prefiltering operation to project from a high-quality offline reconstruction model into our real-time model while suppressing artifacts.
    [Show full text]