Generation of Points That Satisfy Two-Dimensional Elementary Intervals
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Physically Based Rendering: from Theory to Implementation Pdf, Epub, Ebook
PHYSICALLY BASED RENDERING: FROM THEORY TO IMPLEMENTATION PDF, EPUB, EBOOK Matt Pharr, Greg Humphreys, Wenzel Jakob | 1266 pages | 18 Oct 2016 | ELSEVIER SCIENCE & TECHNOLOGY | 9780128006450 | English | San Francisco, United States Physically Based Rendering: From Theory to Implementation PDF Book The text should make more clear that we're making use of the tristimulus theory of color perception in that step. I wrote a technical perspective, The Ray-Tracing Engine That Could , that introduced the article and helped frame the work's achievements for a non-graphics audience. Design and novel uses of higher-dimensional rasterization. Lecture 7: Splines, Curves and Surfaces Shirley et al. Hardcover ISBN: Stanford csb I recently had a great time teaching the and installments of csb, the graduate-level rendering course at Stanford. A practical shading model for ray tracing. Free Shipping Free global shipping No minimum order. Then, in the code below, the negation of 'd' should be removed and in the places where 'd' is added in the computations of tx and ty, subtraction should be used. Toggle navigation pbrt. Feiner, and Kurt Akeley. Osgood this is an outstanding reference Lecture 4: Transforms Shirley et al. I was also fortunate to have the opportunity to teach the class. Given its unconventional preparation style, this textbook stands out because of its descriptions of the tradeoffs involved in developing a complete working renderer. Index of Miscellaneous Identifiers. Wenzel is also the lead developer of the Mitsuba renderer , a research-oriented rendering system. Physically Based Rendering, Second Edition , describes both the mathematical theory behind a modern photorealistic rendering system as well as its practical implementation. -

Rendering Complex Scenes with Memory-Coherent Ray Tracing
To appear in Proceedings of SIGGRAPH 1997 Rendering Complex Scenes with Memory-Coherent Ray Tracing Matt Pharr Craig Kolb Reid Gershbein Pat Hanrahan Computer Science Department, Stanford University Abstract both. For example, Z-buffer rendering algorithms operate on a sin- gle primitive at a time, which makes it possible to build rendering Simulating realistic lighting and rendering complex scenes are usu- hardware that does not need access to the entire scene. More re- ally considered separate problems with incompatible solutions. Ac- cently, the Talisman architecture was designed to exploit frame-to- curate lighting calculations are typically performed using ray trac- frame coherence as a means of accelerating rendering and reducing ing algorithms, which require that the entire scene database reside memory bandwidth requirements[21]. in memory to perform well. Conversely, most systems capable of Kajiya has written a whitepaper that proposes an architecture rendering complex scenes use scan-conversion algorithms that ac- for Monte Carlo ray tracing systems that is designed to improve cess memory coherently, but are unable to incorporate sophisticated coherence across all levels of the memory hierarchy, from pro- illumination. We have developed algorithms that use caching and cessor caches to disk storage[13]. The rendering computation is lazy creation of texture and geometry to manage scene complexity. decomposed into parts—ray-object intersections, shading calcula- To improve cache performance, we increase locality of reference tions, and calculating spawned rays—that are performed indepen- by dynamically reordering the rendering computation based on the dently. The coherence of memory references is increased through contents of the cache. We have used these algorithms to compute careful management of the interaction of the computation and the images of scenes containing millions of primitives, while storing memory that it references, reducing overall running time and facil- ten percent of the scene description in memory. -

Course Overview
Course overview Digital Image Synthesis Yung-Yu Chuang with slides by Mario Costa Sousa, Pat Hanrahan and Revi Ramamoorthi Logistics • Meeting time: 2:20pm-5:20pm, Thursday • Classroom: CSIE Room 111 • Instructor: Yung-Yu Chuang ([email protected]) • TA:陳育聖 • Webpage: http://www.csie.ntu.edu.tw/~cyy/rendering id/password • Mailing list: [email protected] Please subscribe via https://cmlmail.csie.ntu.edu.tw/mailman/listinfo/rendering/ Prerequisites • C++ programming experience is required. • Basic knowledge on algorithm and data structure is essential. • Knowledge on linear algebra, probability, calculus and numerical methods is a plus. • Though not required, it is recommended that you have background knowledge on computer graphics. Requirements (subject to change) • 3 programming assignments (60%) • Class participation (5%) • Final project (35%) Textbook Physically Based Rendering from Theory to Implementation, 2nd ed, by Matt Pharr and Greg Humphreys •Authors have a lot of experience on ray tracing •Complete (educational) code, more concrete •Has been used in many courses and papers •Implement some advanced or difficult-to-implement methods: subdivision surfaces, Metropolis sampling, BSSRDF, PRT. •3rd edition is coming next year! pbrt won Oscar 2014 •ToMatt Pharr, Greg Humphreys and Pat Hanrahan for their formalization and reference implementation of the concepts behind physically based rendering, as shared in their book Physically Based Rendering. Physically based rendering has transformed computer graphics lighting by more accurately simulating materials and lights, allowing digital artists to focus on cinematography rather than the intricacies of rendering. First published in 2004, Physically Based Rendering is both a textbook and a complete source-code implementation that has provided a widely adopted practical roadmap for most physically based shading and lighting systems used in film production. -

An Advanced Path Tracing Architecture for Movie Rendering
RenderMan: An Advanced Path Tracing Architecture for Movie Rendering PER CHRISTENSEN, JULIAN FONG, JONATHAN SHADE, WAYNE WOOTEN, BRENDEN SCHUBERT, ANDREW KENSLER, STEPHEN FRIEDMAN, CHARLIE KILPATRICK, CLIFF RAMSHAW, MARC BAN- NISTER, BRENTON RAYNER, JONATHAN BROUILLAT, and MAX LIANI, Pixar Animation Studios Fig. 1. Path-traced images rendered with RenderMan: Dory and Hank from Finding Dory (© 2016 Disney•Pixar). McQueen’s crash in Cars 3 (© 2017 Disney•Pixar). Shere Khan from Disney’s The Jungle Book (© 2016 Disney). A destroyer and the Death Star from Lucasfilm’s Rogue One: A Star Wars Story (© & ™ 2016 Lucasfilm Ltd. All rights reserved. Used under authorization.) Pixar’s RenderMan renderer is used to render all of Pixar’s films, and by many 1 INTRODUCTION film studios to render visual effects for live-action movies. RenderMan started Pixar’s movies and short films are all rendered with RenderMan. as a scanline renderer based on the Reyes algorithm, and was extended over The first computer-generated (CG) animated feature film, Toy Story, the years with ray tracing and several global illumination algorithms. was rendered with an early version of RenderMan in 1995. The most This paper describes the modern version of RenderMan, a new architec- ture for an extensible and programmable path tracer with many features recent Pixar movies – Finding Dory, Cars 3, and Coco – were rendered that are essential to handle the fiercely complex scenes in movie production. using RenderMan’s modern path tracing architecture. The two left Users can write their own materials using a bxdf interface, and their own images in Figure 1 show high-quality rendering of two challenging light transport algorithms using an integrator interface – or they can use the CG movie scenes with many bounces of specular reflections and materials and light transport algorithms provided with RenderMan. -

(Gpus) for Department of Defense (Dod) Digital Signal Processing (DSP) Applications
Assessment of Graphic Processing Units (GPUs) for Department of Defense (DoD) Digital Signal Processing (DSP) Applications John D. Owens, Shubhabrata Sengupta, and Daniel Horn† University of California, Davis † Stanford University Abstract In this report we analyze the performance of the fast Fourier transform (FFT) on graphics hardware (the GPU), comparing it to the best-of-class CPU implementation FFTW.WedescribetheFFT,thearchitectureoftheGPU,andhowgeneral-purpose computation is structured on the GPU. We then identify the factors that influence FFT performance and describe several experiments that compare these factors between the CPUandtheGPU.Weconcludethattheoverheadoftransferringdataandinitiating GPU computation are substantially higher than on the CPU, and thus for latency- critical applications, the CPU is a superior choice. We show that the CPU imple- mentation is limited by computation and the GPU implementation by GPU memory bandwidth and its lack of a writable cache. The GPU is comparatively better suited for larger FFTs with many FFTs computed in parallel in applications where FFT through- putismostimportant;ontheseapplicationsGPUandCPUperformanceisroughly on par. We also demonstrate that adding additional computation to an application that includes the FFT, particularly computation that is GPU-friendly, puts the GPU at an advantage compared to the CPU. The future of desktop processing is parallel.Thelastfewyearshaveseenanexplosionof single-chip commodity parallel architectures that promises to be the centerpieces of future computing platforms. Parallel hardware on the desktop—new multicore microprocessors, graphics processors, and stream processors—has the potential to greatly increase the com- putational power available to today’s computer users, with a resulting impact in computa- tion domains such as multimedia, entertainment, signal and image processing, and scientific computation. -

Physically-Based Rendering Uses Physics to Simulate the Interaction Between Matter and Light, Realism Is the Primary Goal
Logistics • Meeting time: 2:20pm-5:20pm, Thursday • Classroom: CSIE Room 111 • Instructor: Yung-Yu Chuang ([email protected]) Course overview • TA:賴威昇 • Webpage: http://www.csie.ntu.edu.tw/~cyy/rendering id/password Digital Image Synthesis • Mailing list: [email protected] Yung-Yu Chuang Please subscribe via https://cmlmail.csie.ntu.edu.tw/mailman/listinfo/rendering/ with slides by Mario Costa Sousa, Pat Hanrahan and Revi Ramamoorthi Prerequisites Requirements (subject to change) • C++ programming experience is required. • 3 programming assignments (60%) • Basic knowledge on algorithm and data • Class participation (5%) structure is essential. • Final project (35%) • Knowledge on linear algebra, probability, calculus and numerical methods is a plus. • Though not required, it is recommended that you have background knowledge on computer graphics. Textbook pbrt won Oscar 2014 Physically Based Rendering from Theory to Implementation, •ToMatt Pharr, Greg Humphreys and Pat 2nd ed, by Matt Pharr and Greg Humphreys Hanrahan for their formalization and reference •Authors have a lot of implementation of the concepts behind experience on ray tracing physically based rendering, as shared in their •Complete (educational) code, book Physically Based Rendering. more concrete Physically based rendering has •Has been used in many courses transformed computer graphics lighting by more accurately simulating materials and and papers lights, allowing digital artists to focus on •Implement some advanced or cinematography rather than the intricacies of rendering. First published in difficult-to-implement methods: 2004, Physically Based Rendering is both subdivision surfaces, Metropolis a textbook and a complete source-code sampling, BSSRDF, PRT. implementation that has provided a widely adopted practical roadmap for most •3rd edition is coming next year! physically based shading and lighting systems used in film production. -

01 the Implementation of a Scalable Texture Cache
01 THE IMPLEMENTATION OF A SCALABLE TEXTURE CACHE Matt Pharr 5 March 2017 Abstract Texture caching—loading rectangular tiles of texture maps on demand and keeping a fixed number of them cached in memory—has proven to be an effective approach for limiting memory use when rendering complex scenes; scenes with gigabytes of texture can often be rendered with just tens or hundreds of megabytes of texture resident in memory. However, implementing an efficient texture cache is challenging in the presence of tens of rendering threads; each traced ray generally performs multiple cache lookups, one for each texel accessed during texture filtering, all while new tiles are being added to the cache and old tiles are recycled. Traditional thread synchronization approaches based on mutexes give poor parallel scalability with this workload. We present a texture cache implementation based on lock-free algorithms and the “read-copy update” technique, and show that it scales linearly up to (at least) 32 threads. Our implementation performs just as well as pbrt does with preloaded textures where there are no such cache maintenance complexities. Note: This document describes new functionality that may be included in a future version of pbrt. The implementation is available in the texcache branch in the pbrt-v3 repository on github. We’re interested in feedback (especially bug reports) about our implementation; please send a note to [email protected] or post to the pbrt Google Groups list if you have comments or questions. (Given that the implementation does some fairly tricky things to minimize locking and inter-thread coordination, it is entirely possible that subtle bugs remain.) 1.1 INTRODUCTION Most visually complex computer graphics scenes make extensive use of tex- ture maps to represent variation in surface appearance. -

The Path to Path-Traced Movies
Full text available at: http://dx.doi.org/10.1561/0600000073 The Path to Path-Traced Movies Per H. Christensen Pixar Animation Studios [email protected] Wojciech Jarosz Dartmouth College [email protected] Boston — Delft Full text available at: http://dx.doi.org/10.1561/0600000073 Foundations and Trends R in Computer Graphics and Vision Published, sold and distributed by: now Publishers Inc. PO Box 1024 Hanover, MA 02339 United States Tel. +1-781-985-4510 www.nowpublishers.com [email protected] Outside North America: now Publishers Inc. PO Box 179 2600 AD Delft The Netherlands Tel. +31-6-51115274 The preferred citation for this publication is P. H. Christensen and W. Jarosz. The Path to Path-Traced Movies. Foundations and Trends R in Computer Graphics and Vision, vol. 10, no. 2, pp. 103–175, 2014. R This Foundations and Trends issue was typeset in LATEX using a class file designed by Neal Parikh. Printed on acid-free paper. ISBN: 978-1-68083-211-2 c 2016 P. H. Christensen and W. Jarosz All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, mechanical, photocopying, recording or otherwise, without prior written permission of the publishers. Photocopying. In the USA: This journal is registered at the Copyright Clearance Cen- ter, Inc., 222 Rosewood Drive, Danvers, MA 01923. Authorization to photocopy items for internal or personal use, or the internal or personal use of specific clients, is granted by now Publishers Inc for users registered with the Copyright Clearance Center (CCC). -

Advanced Renderman 3: Render Harder
Advanced RenderMan 3: Render Harder SIGGRAPH 2001 Course 48 course organizer: Larry Gritz, Exluna, Inc. Lecturers: Tony Apodaca, Pixar Animation Studios Larry Gritz, Exluna, Inc. Matt Pharr, Exluna, Inc. Christophe Hery, Industrial Light + Magic Kevin Bjorke, Square USA Lawrence Treweek, Sony Pictures Imageworks August 2001 ii iii Desired Background This course is for graphics programmers and technical directors. Thorough knowledge of 3D image synthesis, computer graphics illumination models and previous experience with the RenderMan Shading Language is a must. Students must be facile in C. The course is not for those with weak stomachs for examining code. Suggested Reading Material The RenderMan Companion: A Programmer’s Guide to Realistic Computer Graphics, Steve Upstill, Addison-Wesley, 1990, ISBN 0-201-50868-0. This is the basic textbook for RenderMan, and should have been read and understood by anyone attending this course. Answers to all of the typical, and many of the extremely advanced, questions about RenderMan are found within its pages. Its failings are that it does not cover RIB, only the C interface, and also that it only covers the 10-year- old RenderMan Interface 3.1, with no mention of all the changes to the standard and to the products over the past several years. Nonetheless, it still contains a wealth of information not found anyplace else. Advanced RenderMan: Creating CGI for Motion Pictures, Anthony A. Apodaca and Larry Gritz, Morgan-Kaufmann, 1999, ISBN 1-55860-618-1. A comprehensive, up-to-date, and advanced treatment of all things RenderMan. This book covers everything from basic RIB syntax to the geometric primitives to advanced topics like shader antialiasing and volumetric effects. -

Ray Casting (Appel, 1968) Ray Casting (Appel, 1968) Ray Casting (Appel, 1968) Ray Casting (Appel, 1968)
Logistics • Meeting time: 2:20pm-5:20pm, Thursday • Classroom: CSIE Room 111 • Instructor: Yung-Yu Chuang ([email protected]) Course overview • TA:陳育聖 • Webpage: http://www.csie.ntu.edu.tw/~cyy/rendering id/password Digital Image Synthesis • Mailing list: [email protected] Yung-Yu Chuang Please subscribe via https://cmlmail.csie.ntu.edu.tw/mailman/listinfo/rendering/ with slides by Mario Costa Sousa, Pat Hanrahan and Revi Ramamoorthi Prerequisites Requirements (subject to change) • C++ programming experience is required. • 3 programming assignments (60%) • Basic knowledge on algorithm and data • Class participation (5%) structure is essential. • Final project (35%) • Knowledge on linear algebra, probability, calculus and numerical methods is a plus. • Though not required, it is recommended that you have background knowledge on computer graphics. Textbook pbrt won Oscar 2014 Physically Based Rendering from Theory to Implementation, •ToMatt Pharr, Greg Humphreys and Pat 2nd ed, by Matt Pharr and Greg Humphreys Hanrahan for their formalization and reference •Authors have a lot of implementation of the concepts behind experience on ray tracing physically based rendering, as shared in their •Complete (educational) code, book Physically Based Rendering. more concrete Physically based rendering has •Has been used in many courses transformed computer graphics lighting by more accurately simulating materials and and papers lights, allowing digital artists to focus on •Implement some advanced or cinematography rather than the intricacies of rendering. First published in difficult-to-implement methods: 2004, Physically Based Rendering is both subdivision surfaces, Metropolis a textbook and a complete source-code sampling, BSSRDF, PRT. implementation that has provided a widely adopted practical roadmap for most •3rd edition is coming next year! physically based shading and lighting systems used in film production. -
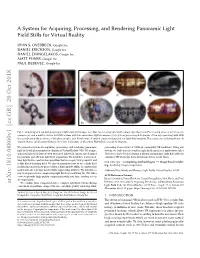
A System for Acquiring, Processing, and Rendering Panoramic Light Field Stills for Virtual Reality
A System for Acquiring, Processing, and Rendering Panoramic Light Field Stills for Virtual Reality RYAN S. OVERBECK, Google Inc. DANIEL ERICKSON, Google Inc. DANIEL EVANGELAKOS, Google Inc. MATT PHARR, Google Inc. PAUL DEBEVEC, Google Inc. (a) (b) (e) (f) (g) (c) (d) (h) (i) (j) Fig. 1. Acquiring and rendering panoramic light field still images. (a,c) Our two rotating light field camera rigs: the 16×GoPro rotating array of action sports cameras (a), and a multi-rotation 2×DSLR system with two mirrorless digital cameras (c). (b,d) Long exposure photographs of the rigs operating with LED traces indicating the positions of the photographs. (e-j) Novel views of several scenes rendered by our light field renderer. The scenes are: (e) Living Room, (f) Gamble House, (g) Discovery Exterior, (h) Cheri & Gonzalo, (i) Discovery Flight Deck, and (j) St. Stephens. We present a system for acquiring, processing, and rendering panoramic generating stereo views at 90Hz on commodity VR hardware. Using our light field still photography for display in Virtual Reality (VR). We acquire system, we built a freely available light field experience application called spherical light field datasets with two novel light field camera rigs designed Welcome to Light Fields featuring a library of panoramic light field stills for for portable and efficient light field acquisition. We introduce a novel real- consumer VR which has been downloaded over 15,000 times. time light field reconstruction algorithm that uses a per-view geometry and CCS Concepts: • Computing methodologies → Image-based render- a disk-based blending field. We also demonstrate how to use a light field ing; Rendering; Image compression; prefiltering operation to project from a high-quality offline reconstruction model into our real-time model while suppressing artifacts. -

Physically Based Rendering: from Theory to Implementation Download Free Book
PHYSICALLY BASED RENDERING: FROM THEORY TO IMPLEMENTATION DOWNLOAD FREE BOOK Matt Pharr, Greg Humphreys, Wenzel Jakob | 1266 pages | 18 Oct 2016 | ELSEVIER SCIENCE & TECHNOLOGY | 9780128006450 | English | San Francisco, United States Physically Based Rendering Primitives and Intersection Acceleration Chapter 5. Through a method known as 'literate programming', the authors combine human-readable documentation and source code into a single reference that is specifically designed to aid comprehension. Sorry, this product is currently out of stock. His research interests revolve around material appearance modeling, rendering algorithms, and the high-dimensional geometry of light paths. View 1 excerpt, cites methods. He has a B. Many PBR pipelines have the accurate simulation of photorealism as their goal. Sophisticated applications allow savvy users to write custom shaders in a shading language such as HLSL or GLSLthough increasingly node-based material editors that allow a graph-based workflow with native support for important concepts such as light position, levels of reflection and emission and metallicity, and a wide range of other math and optics functions are replacing hand-written shaders for all but the most complex applications. On filtering the noise from the random parameters in Monte Carlo rendering. Environments can be defined with procedural shaders or textures as well as procedural geometry or meshes or pointclouds [9]. Wenzel is also the lead developer of the Mitsuba renderera research-oriented rendering system. From Wikipedia, the free encyclopedia. All Pages Books Journals. Thanks in advance for your time. Greg has a B. Sorry, this product is currently unavailable. Before that, he was a professor of Computer Science at the University of Virginia, where he conducted research in both high performance and physically based computer graphics, as well as computer architecture and visualization.