Gamma Spectroscopy Following the Beta-Decay of Neutron Rich Nuclei At
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Experimental Γ Ray Spectroscopy and Investigations of Environmental Radioactivity
Experimental γ Ray Spectroscopy and Investigations of Environmental Radioactivity BY RANDOLPH S. PETERSON 216 α Po 84 10.64h. 212 Pb 1- 415 82 0- 239 β- 01- 0 60.6m 212 1+ 1630 Bi 2+ 1513 83 α β- 2+ 787 304ns 0+ 0 212 α Po 84 Experimental γ Ray Spectroscopy and Investigations of Environmental Radioactivity Randolph S. Peterson Physics Department The University of the South Sewanee, Tennessee Published by Spectrum Techniques All Rights Reserved Copyright 1996 TABLE OF CONTENTS Page Introduction ....................................................................................................................4 Basic Gamma Spectroscopy 1. Energy Calibration ................................................................................................... 7 2. Gamma Spectra from Common Commercial Sources ........................................ 10 3. Detector Energy Resolution .................................................................................. 12 Interaction of Radiation with Matter 4. Compton Scattering............................................................................................... 14 5. Pair Production and Annihilation ........................................................................ 17 6. Absorption of Gammas by Materials ..................................................................... 19 7. X Rays ..................................................................................................................... 21 Radioactive Decay 8. Multichannel Scaling and Half-life ..................................................................... -

Nuclear Engineering and Technology 49 (2017) 1489E1494
Nuclear Engineering and Technology 49 (2017) 1489e1494 Contents lists available at ScienceDirect Nuclear Engineering and Technology journal homepage: www.elsevier.com/locate/net Original Article Large-volume and room-temperature gamma spectrometer for environmental radiation monitoring * Romain Coulon , Jonathan Dumazert, Tola Tith, Emmanuel Rohee, Karim Boudergui CEA, LIST, F-91191 Gif-sur-Yvette Cedex, France article info abstract Article history: The use of a room-temperature gamma spectrometer is an issue in environmental radiation monitoring. Received 29 April 2016 To monitor radionuclides released around a nuclear power plant, suitable instruments giving fast and Received in revised form reliable information are required. High-pressure xenon (HPXe) chambers have range of resolution and 15 May 2017 efficiency equivalent to those of other medium resolution detectors such as those using NaI(Tl), CdZnTe, Accepted 4 June 2017 and LaBr :Ce. An HPXe chamber could be a cost-effective alternative, assuming temperature stability and Available online 3 July 2017 3 reliability. The CEA LIST actively studied and developed HPXe-based technology applied for environ- mental monitoring. Xenon purification and conditioning was performed. The design of a 4-L HPXe de- Keywords: Xenon tector was performed to minimize the detector capacitance and the required power supply. Simulations fi Spectrometry were done with the MCNPX2.7 particle transport code to estimate the intrinsic ef ciency of the HPXe Environmental detector. A behavioral study dealing with ballistic deficits and electronic noise will be utilized to provide Detector perspective for further analysis. Radiation © 2017 Korean Nuclear Society, Published by Elsevier Korea LLC. This is an open access article under the Ionization chamber CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/). -
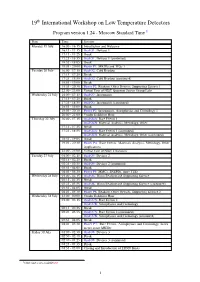
19 International Workshop on Low Temperature Detectors
19th International Workshop on Low Temperature Detectors Program version 1.24 - Moscow Standard Time 1 Date Time Session Monday 19 July 16:00 - 16:15 Introduction and Welcome 16:15 - 17:15 Oral O1: Devices 1 17:15 - 17:25 Break 17:25 - 18:55 Oral O1: Devices 1 (continued) 18:55 - 19:05 Break 19:05 - 20:00 Poster P1: MKIDs and TESs 1 Tuesday 20 July 16:00 - 17:15 Oral O2: Cold Readout 17:15 - 17:25 Break 17:25 - 18:55 Oral O2: Cold Readout (continued) 18:55 - 19:05 Break 19:05 - 20:30 Poster P2: Readout, Other Devices, Supporting Science 1 22:00 - 23:00 Virtual Tour of NIST Quantum Sensor Group Labs Wednesday 21 July 16:00 - 17:15 Oral O3: Instruments 17:15 - 17:25 Break 17:25 - 18:55 Oral O3: Instruments (continued) 18:55 - 19:05 Break 19:05 - 20:30 Poster P3: Instruments, Astrophysics and Cosmology 1 20:00 - 21:00 Vendor Exhibitor Hour Thursday 22 July 16:00 - 17:15 Oral O4A: Rare Events 1 Oral O4B: Material Analysis, Metrology, Other 17:15 - 17:25 Break 17:25 - 18:55 Oral O4A: Rare Events 1 (continued) Oral O4B: Material Analysis, Metrology, Other (continued) 18:55 - 19:05 Break 19:05 - 20:30 Poster P4: Rare Events, Materials Analysis, Metrology, Other Applications 22:00 - 23:00 Virtual Tour of NIST Cleanoom Tuesday 27 July 01:00 - 02:15 Oral O5: Devices 2 02:15 - 02:25 Break 02:25 - 03:55 Oral O5: Devices 2 (continued) 03:55 - 04:05 Break 04:05 - 05:30 Poster P5: MMCs, SNSPDs, more TESs Wednesday 28 July 01:00 - 02:15 Oral O6: Warm Readout and Supporting Science 02:15 - 02:25 Break 02:25 - 03:55 Oral O6: Warm Readout and Supporting -

Supplement to The
Hahn-Meitner-Institut Berlin Supplement to the Annual Report 2001 Berlin 2002 Supplement Index Publications 3 Structural Research 4 Solar Energy Research 21 Information Technology 30 Conference Contributions / Invited Lectures 31 Structural Research 32 Solar Energy Research 62 Information Technology 77 Technology Transfer / Patents 79 Academic Education 83 Courses 84 Exams 87 Co-operation Partners and Guests 89 Structural Research 90 Solar Energy Research 99 Information Technology 103 External Funding 105 Structural Research 106 Solar Energy Research 108 Participation in External Scientific Bodies and Committees 111 Miscellaneous 115 Awards / Exhibitions / Fairs / Organization of Conferences and Meetings / Events 1. Edition June 2002 Supplement of the Annual Report 2001 HMI-B 585 Hahn-Meitner-Institut Berlin GmbH Glienicker Str. 100 D-14109 Berlin (Wannsee) Coordination: Maren Achilles Phone: +49 – (0)30 – 8062 2668 Fax: +49 – (0)30 – 8062 2047 E-mail: [email protected] A 2 HMI Annual Report 2001 Publications 2001 Publications HMI Annual Report 2001 A 3 Publications 2001 Structural Research Department SF1 Pappas, C.; Kischnik, R.; Mezei, F. Wide angle NSE : the spectrometer SPAN at Instruments and Methods BENSC Physica B 297 (2001) 14-17 Pappas, C.; Mezei, F. Reviewed Publications How to achieve high intensity in NSE spectros- copy? BENSC-Activities Proceedings of the ILL Millenium Workshop, 2001, p.318 Ehlers, G.; Farago, B;. Pappas, C; Mezei, F. A new IN11 with an almost 35 times higher Peters, J.; Treimer, W. counting rate than that of IN11C Bloch walls in a nickel single crystal Proceedings of the ILL Millenium Workshop, 2001 p. Phys. Rev. B 64 (2001) 214415 – 214422 316 Scheffer, M.; Rouijaa, M.; Suck, J.-B.; Sterzel, R.; Fitzsimmons, M. -

Gamma Ray Spectroscopy
Gamma Ray Spectroscopy Ian Rittersdorf Nuclear Engineering & Radiological Sciences [email protected] March 20, 2007 Rittersdorf Gamma Ray Spectroscopy Contents 1 Abstract 3 2 Introduction & Objectives 3 3 Theory 4 3.1 Gamma-Ray Interactions . 5 3.1.1 Photoelectric Absorption . 5 3.1.2 Compton Scattering . 6 3.1.3 Pair Production . 8 3.2 Detector Response Function . 9 3.3 Complications in the Response Function . 11 3.3.1 Secondary Electron Escape . 11 3.3.2 Bremsstrahlung Escape . 12 3.3.3 Characteristic X-Ray Escape . 12 3.3.4 Secondary Radiations Created Near the Source . 13 3.3.5 Effects of Surrounding Materials . 13 3.3.6 Summation Peaks . 14 3.4 Semiconductor Diode Detectors . 15 3.5 High Purity Germanium Semiconductor Detectors . 17 3.5.1 HPGe Geometry . 18 3.6 Germanium Detector Setup . 18 3.7 Energy Resolution . 19 3.8 Background Radiation . 20 4 Equipment List 21 5 Setup & Settings 21 6 Analysis 23 6.1 Prominent Peak Information . 24 6.2 Calibration Curve . 24 6.3 Experiment Part 6 – 57Co ............................ 26 6.4 Experiment Part 6 – 60Co ............................ 28 6.5 Experiment Part 6 – 137Cs............................ 29 6.6 Experiment Part 6 – 22Na ............................ 31 6.7 Experiment Part 6 – 133Ba............................ 32 6.8 Experiment Part 6 – 109Cd............................ 34 6.9 Experiment Part 6 – 54Mn............................ 35 6.10 Energy Resolution . 37 6.11 Background Analysis . 39 1 Rittersdorf Gamma Ray Spectroscopy 7 Conclusions 43 Appendices i A 57Co Decay Scheme i B 60Co Decay Scheme ii C 137Cs Decay Scheme iii D 22Na Decay Scheme iv E 133Ba Decay Scheme v F 109Cd Decay Scheme vi G 54Mn Decay Scheme vii H HPGe Detector Apparatus viii I Raw Gamma-Ray Spectra ix References ix 2 Rittersdorf Gamma Ray Spectroscopy 1 Abstract In lab, a total of eight spectra were measured. -

Detecting, Monitoring, and Sampling Hazardous Materials
Analyzing the Incident: Detecting, Monitoring, and Sampling Hazardous Materials Chapter Contents Exposure .......................................161 Thermal Imagers .......................................................188 Routes of Entry ..........................................................161 Infrared Thermometers .............................................188 Contamination versus Exposure ...............................162 Other Detection Devices .....................189 Acute versus Chronic Exposure ................................163 Halogenated Hydrocarbon Meters ............................189 Radiological and Biological Exposures ...164 Flame Ionization Detectors ........................................190 Exposure Limits .........................................................164 Gas Chromatography .................................................190 Radiological Exposures .............................................168 Mass Spectroscopy ...................................................191 Biological Exposures .................................................169 Ion Mobility Spectrometry ........................................192 Sensor-Based Instruments and Surface Acoustic Wave ..............................................192 Other Devices ...............................170 Gamma-Ray Spectrometer ........................................193 Oxygen Indicators .....................................................170 Fourier Transform IR .................................................194 Combustible Gas Indicators -

Testing FLUKA on Neutron Activation of Si and Ge at Nuclear Research Reactor Using Gamma Spectroscopy
Testing FLUKA on neutron activation of Si and Ge at nuclear research reactor using gamma spectroscopy J. Bazoa, J.M. Rojasa, S. Besta, R. Brunab, E. Endressa, P. Mendozac, V. Pomac, A.M. Gagoa aSecci´onF´ısica, Departamento de Ciencias, Pontificia Universidad Cat´olica del Per´u,Av. Universitaria 1801, Lima 32, Per´u bC´alculoAn´alisisy Seguridad (CASE), Instituto Peruano de Energ´ıaNuclear (IPEN), Av. Canad´a1470, Lima 41, Per´u cDivisi´onde T´ecnicas Anal´ıticas Nucleares, Instituto Peruano de Energ´ıaNuclear (IPEN), Av. Canad´a1470, Lima 41, Per´u Abstract Samples of two characteristic semiconductor sensor materials, silicon and ger- manium, have been irradiated with neutrons produced at the RP-10 Nuclear Research Reactor at 4.5 MW. Their radionuclides photon spectra have been measured with high resolution gamma spectroscopy, quantifying four radioiso- topes (28Al, 29Al for Si and 75Ge and 77Ge for Ge). We have compared the radionuclides production and their emission spectrum data with Monte Carlo simulation results from FLUKA. Thus we have tested FLUKA's low energy neutron library (ENDF/B-VIIR) and decay photon scoring with respect to the activation of these semiconductors. We conclude that FLUKA is capable of pre- dicting relative photon peak amplitudes, with gamma intensities greater than 1%, of produced radionuclides with an average uncertainty of 13%. This work allows us to estimate the corresponding systematic error on neutron activation simulation studies of these sensor materials. Keywords: FLUKA, neutron irradiation, nuclear reactor, silicon, germanium arXiv:1709.02026v2 [physics.ins-det] 21 Dec 2017 ∗Corresponding author Email address: [email protected] (J. -

Progress in Investigation of Wwer-440 Reactor Pressure Vessel Steel by Gamma and Mossbauer Spectroscopy
HR9800123 PROGRESS IN INVESTIGATION OF WWER-440 REACTOR PRESSURE VESSEL STEEL BY GAMMA AND MOSSBAUER SPECTROSCOPY J. Hascik1. V. Slugen', J. Lipka1, RKupca2, R Hinca', I. Toth', R Grone', P. Uvacik1 'Department of Nuclear Physics and Technology, Slovak University of Technology, Ilkovicova3, 81219 Bratislava, Slovakia 2NPP Research Institute, Trnava, Okruznd 5, Slovakia Abstract Gramma spectroscopic analyse and first experimental results of original irradiated reactor pressure vessel surveillance specimens are discussed in . In 1994, the new "Extended Surveillance Specimen Program for Nuclear Reactor Material Study" was started in collaboration with the nuclear power plants (NPP) V-2 Bohunice (Slovakia). The first batch of MS samples (after 1 year, which is equivalent to 5 years of loading RPV-steel) was measured and interpreted using the new four components approach with the aim to observe microstructural changes due to thermal and neutron treatment resulting from operating conditions in NPP. The systematic changes in the relative areas of Mossbauer spectra components were observed. 1 INTRODUCTION The reactor pressure vessel (RPV) is probably the most important component of a nuclear power plant (NPP) and its condition significantly affects the NPP's lifetime and operational characteristics. One of the basic requirements in nuclear reactor technique is ensuring the sufficient safety margin and reliability of used materials during their operational mechanical, thermal or radiation treatment [1]. In framework of Extended Surveillance Specimen Program 24 specimens, designed especially for MS measurement, were selected and measured in "as received" state, before their placement into the core of the operated nuclear reactor. Mossbauer spectra, which correspond to the basic material samples, show typical behaviour of dilute iron alloys and can be described with three [2,3] or four sextets. -

Devices of Basic and Applied Scientific Research Center
أﺟﻬﺰة ﻣﺮﻛﺰ اﻟﺒﺤﻮث اﻟﻌﻠﻤﻴﺔ اﺳﺎﺳﻴﺔ و اﻟﺘﻄﺒﻴﻘﻴﺔ Devices of Basic and Applied Scientic Research Center Done by 2018 Ibtisam H. Al-Qahtani Content Introduction Research units labs information Key Devises at the Research Units Labs Research Units Labs Services Gamma -ray Spectroscopy X-Ray Diffractometer (XRD- 7000) Organic Elemental Analyzer Tot al Organic Carbon Analyzer (TOC) Fourier Transform Infrared Analysis System- (FTIR) Gas Chromatography – Mass spectrometer (GC-MS/MS) Microwave Digestion System Thermo-Gravimetric Analyzer (TGA) UV SolidSpec-3700 Inductively Coupled Plasma (ICP) LCMS - 8040 with APCI High Energy E-max Ball Energy Dispersive -X Ray Fluorescence spectrometers (EDXRF) Automated Surface Area Analyzer DXR Raman Microscope Analytical Scanning Electron Microscopy (VEGA 3) Atomic Absorption Spectrophotometer (AAS) TASLIMAGE Radon Dosimetry System Flash Chromatography Ion Chromatography System S 153- A Dual GasChromatograph (GC-2014 ) VITEK® 2 Compact DAKO ARTIZAN (Multi Strainer) DAKO Hematoxylin 1 - Introductiongreat atte lies in the scientific, intellectual and behavioural capacities of its sons . The need for Thestudies, Kingdom research of Saudi and Arabia learning has recently has become taken serious a cornerstone steps and insteps life toto reach thestrengthen greatest its possible position knowledge in science and of technology,the sciences achieve that ensureeconomic the renaissance well-being and of the humanaddress being, the andmost ensure important the problems superiority it faces of others,at the national as developed level . countries pay great attentionThese to scientific efforts stem research from the for desire its realization of good leadership that the togreatness move from of a nations natural lies in the scientific, intellectual and behavioural capacities of its sons. -

Experiment 3 Gamma-Ray Spectroscopy Using Nai(Tl)
ORTEC ® Experiment 3 Gamma-Ray Spectroscopy Using NaI(Tl) Equipment Required • SPA38 Integral Assembly consisting of a 38 mm x 38 mm • RSS8 * Gamma Source Set. Includes ~1 µCi each of: 60 Co, 137 Cs, NaI(Tl) Scintillator, Photomultiplier Tube, and PMT Base with 22 Na, 54 Mn, 133 Ba, 109 Cd, 57 Co, and a mixed Cs/Zn source (~0.5 Stand µCi 137 Cs, ~1 µCi 65 Zn). The first three are required in this • 4001A/4002D NIM Bin and Power Supply experiment. An unknown for Experiment 3.2 can be selected from the remaining sources. • 556 High Voltage Bias Supply • GF-137-M-5 * 5 µCi ±5% 137 Cs Gamma Source (used as a • 113 Scintillation Preamplifier reference standard for activity in Experiment 3.5). • 575A Spectroscopy Amplifier • GF-057-M-20 * 20 µCi 57 Co Source (for Experiment 3.9). • EASY-MCA-2K including USB cable and MAESTRO software • One each of pure metal foil absorber sets: FOIL-AL-30 , FOIL- (other ORTEC MCAs may be substituted) FE-5 , FOIL-CU-10 , FOIL-MO-3 , FOIL-SN-4 , and FOIL-TA-5 . • Personal Computer with a USB port and a recent, supportable Each set contains 10 identical foils of the designated pure version of the Windows operating system. element and thickness in thousandths of an inch (Foil-Element- Thickness). • TDS3032C Oscilloscope with a bandwidth ≥150 MHz. • RAS20 Absorber Foil Kit containing 5 lead absorbers from 1100 • C-34-12 RG-59A/U 75- Ω Cable with one SHV female plug and to 7400 mg/cm 2. -

FY-2010 Process Monitoring Technology Final Report
PNNL-20022 Prepared for the U.S. Department of Energy under Contract DE-AC05-76RL01830 FY-2010 Process Monitoring Technology Final Report CR Orton JJ Henkel JM Peterson SA Bryan JM Schwantes DE Verdugo AJ Casella EA Jordan RN Christensen JW Hines AM Lines SM Peper TG Levitskaia CG Fraga January 2011 PNNL-20022 FY-2010 Process Monitoring Technology Final Report CR Orton1 JJ Henkel3 JM Peterson1 SA Bryan1 JM Schwantes1 DE Verdugo1 AJ Casella1 EA Jordan1 RN Christensen2 JW Hines3 AM Lines1 SM Peper1 TG Levitskaia1 CG Fraga1 January 2011 Prepared for the U.S. Department of Energy under Contract DE-AC05-76RL01830 Pacific Northwest National Laboratory Richland, Washington 99352 1 Pacific Northwest National Laboratory, Richland, Washington 2 The Ohio State University, Columbus, Ohio 3 University of Tennessee, Knoxville, Tennessee Executive Summary The diversion of special nuclear materials (SNM) and the monitoring of process conditions within nuclear reprocessing facilities are of significant interest to international safeguards facility regulators (e.g., the International Atomic Energy Agency (IAEA)) as well as nuclear material reprocessing facility operators. For large throughput nuclear facilities, such as commercial reprocessing plants, it is difficult to satisfy the IAEA safeguards accountancy goal for detection of abrupt diversion. Process monitoring helps detect diversion by using process control measurements to detect abnormal plant operation. In recent years, the Office of Nuclear Safeguards and Security (NA-241) at the National Nuclear Security Administration (NNSA) has funded a Process Monitoring Working Group (PMWG) to study various mechanisms for diverting nuclear material from spent nuclear fuel (SNF) reprocessing facilities. Common approaches for diverting special nuclear material can occur via removal of separated bulk nuclear materials, or more likely, from minor modifications to processing conditions. -

Other Major Instrumentation
Major instrumentation, Department of Chemistry & Biochemistry - August 18, 2021 Category Instrument 1. Spectroscopy Agilent 6530 q-TOF LC/MS Diamond ATR Golden Gate Accessory 7700 Agilent ICP-MS inductively coupled plasma-mass spectrometer with laser ablation interface Thermo Nicolet Nexus 6700 FT-IR with HATR accessory Thermo Nicolet 380 FT-IR infrared spectrometer Thermo Nicolet Nexus 6700 FT-IR Bruker Avance 600 MHz NMR with Broadband and Variable Temperature Capabilities + $3,000 2013 workstation upgrade. Bruker Vertex 70 FT-IR Rudolph Research Polarimeter JEOL JMS-T100DART AccuTOF Mass Spectrometer with AP-MALDI and ESI Power Technology Laser system, Diod laser blue 405 nm and 50 MW outtput Beckmann Coulter Fluorescence DTX 880 multimode Plate Reader Thermo Nanodrop Spectrometer Biotek H4 Microplate Spectrophotometer Agilent Diode Array 8453 Spectrophotometer Quantech Fluorometer Biotek Eon Microplate Spectrophotometer RBD Sputter gun and accessories Hiden Analytical Mass Spectrometer and UHV chamber and Accessories Vacuum Pumps 16 inch spherical UHV chamber CHAM-5-16 Bruker DPX-300 NMR with QNP and Broadband Probes, and VT Accessory McAllister Tech Services - XYZ Manipulator system MB3004-SP Lamba Bio+ UV/Vis Spectrophotometers (SN 3104) Oriel Instruments Nitrogen Laser Shimadzu UV-1601 UV-Vis Spectrophotometer (SN A10753782123) Shimadzu UV-1601 UV-Vis Spectrophotometer SpectraTech Inspect IR LSI Nitrogen Laser Nicolet Avatar 370 FT-IR infrared spectrometer Agilent Diode Array 8453 Spectrophotometer Lambda 35 UV-Vis Spectrophotometer