DOCSLIB.ORG

The Observed Structure of Extremely Distant Galaxies

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Observed Structure of Extremely Distant Galaxies Astronomy Letters, Vol. 28, No. 1, 2002, pp. 1–11. Translated from Pis’ma v Astronomicheski˘ı Zhurnal, Vol. 28, No. 1, 2002, pp. 3–13. Original Russian Text Copyright c 2002 by Reshetnikov, Vasil’ev. The Observed Structure of Extremely Distant Galaxies V. P. Reshetnikov * and A. A. Vasil’ev Astronomical Institute, St. Petersburg State University, Bibliotechnaya pl. 2, Petrodvorets, 198904 Russia Received July 18, 2001 Abstract—We have identified 22 galaxies with photometric redshifts zph = 5–7in the northern and southern Hubble Space Telescope deep fields. An analysis of the images of these objects shows that they are asymmetric and very compact (∼1 kpc) structures with high surface brightness and absolute m magnitudes of MB ≈−20 . The average spectral energy distribution for these galaxies agrees with the distributions for galaxies with active star formation. The star formation rate in galaxies with zph =5–7 −1 was estimated from their luminosity at λ = 1500 Atobe˚ ∼30 M yr . The spatial density of these objects is close to the current spatial density of bright galaxies. All the above properties of the distant galaxies considered are very similar to those of the so-called Lyman break galaxies (LBGs) with z ∼ 3–4. The similarity between the objects considered and LBGs suggests that at z ∼ 6, we observe the progenitors of present-day galaxies that form during mergers of protogalactic objects and that undergo intense starbursts. c 2002 MAIK “Nauka/Interperiodica”. Key words: theoretical and observational cosmology; galaxies, groups and clusters of galaxies, intergalactic gas INTRODUCTION Fields) and the technique capable of identifying them (photometric redshifts). The Hubble Space Telescope (HST) and major ground-based telescopes allowed several galaxies Hubble Deep Fields (northern and southern— (not quasars or radio galaxies) at large “cosmolog- HDF-N and HDF-S) are currently the deepest ical” redshifts to be identified and studied in recent “punctures” made into the Universe (Ferguson et al. years (Stern and Spinrad 1999). For instance, objects 2000). In these two small areas (each with a size with redshifts z =5.60 (Weymann et al. 1998) and of ∼5.3 arcmin2) several thousand objects have been m z =5.34 (Spinrad et al. 1998) have been discovered identified down to a limiting magnitude of V ∼ 30 . in the northern Hubble Deep Field. Other galaxies Each Deep Field pixel has an angular size of only with z =5.34 (Dey et al. 1998), z =5.74 (Hu et al. 0.04, which allows objects with sizes ∼1 kpc to be 1999), and z =5.63 (Dawson et al. 2001) are also resolved at almost all z.Originalfield images were known. The importance given to searches for such obtained in F300W, F450W, F606W, and F814W extremely distant and, therefore, very young objects broadband filters (numbers in filter names indicate the is quite understandable, because they serve as crucial central wavelength in nanometers). These filters are tests for modern models of galaxy formation and also often referred to as U300, B450, V606,andI814 because allow the processes in the relatively early Universe to of their relative proximity to the corresponding stan- be studied. dard filters. Later, HST and ground-based infrared The principal aim of our work is to attempt to (JHK) images of the deep fields were taken. These analyze the observed structure of the most distant additional data were obtained mostly with lower objects identified in deep fields in the spectral region angular resolution and lower limiting magnitude. at the boundary between the optical and the infrared. We decided to analyze objects located in two fields and having redshifts ranging from 5 to 7. The up- per limit is due to the fact that at z>7 the part of GALAXY SAMPLE the galactic spectrum with λ0 > 1216 A(˚ λ0 is the The goal of this work unambiguously defines both wavelength in the restframe of the galaxy) falls beyond the region to be searched for the objects we are in- the passband of the I814 filter (the longest wavelength terested in (the northern and southern Hubble Deep filter in which the original deep-field images are ob- tained). At λ0 < 1216 A,˚ the observed flux from dis- * E-mail: Öe×h@a×ØÖÓº×ÔbÙºÖÙ tant objects decreases abruptly due to absorption by 1063-7737/02/2801-0001$22.00 c 2002 MAIK “Nauka/Interperiodica” 2 RESHETNIKOV, VASIL’EV Table 1. Galaxies in HDF-N Table 2. Galaxies in HDF-S N Name I814(AB) zsp zph Type N Name I814(AB) zph Type 3a 3-951.1 26.20 5.34 5.25 Irr 0036 SB-WF-0393-1295 29.86 6.75 Scd 3b 3-951.2 26.95 5.34 5.25 Irr 0089 SB-WF-0648-0506 28.53 5.49 Scd 213 4-473.0 27.17 5.60 5.95 Irr 0277 SB-WF-1510-1270 29.60 6.63 Sbc 328 4-200.0 26.19 – 5.20 Irr 0400 SB-WF-1947-1654 28.23 6.52 SB1 343 3-543.0 27.78 – 5.95 Irr 0470 SB-WF-2127-1818 29.77 6.85 SB1 0543 SB-WF-2328-3923 27.55 5.12 SB2 367 3-489.0 26.74 – 5.18 Irr 0611 SB-WF-2434-2255 28.28 5.20 Irr 576 3-228.0 26.93 – 5.58 Irr 0696 SB-WF-2611-1523 28.73 5.26 SB1 658 4-799.0 27.30 – 5.33 Irr 0881 SB-WF-3032-2976 29.19 6.01 Irr 714 3-44.0 27.20 – 5.29 Irr 0886 SB-WF-3049-1323 28.07 5.56 SB2 0932 SB-WF-3144-0926 29.10 6.94 SB1 intergalactic HI clouds (Madau 1995). We therefore cannot expect the images of more distant objects to 1079 SB-WF-3473-1780 28.93 5.22 SB2 be seen in the I814 band. The lower limit (z>5) is set 1097 SB-WF-3516-0827 29.25 5.72 Irr arbitrarily. that mutually independent data by Fernandez-Soto Recall that the age-redshift dependence is strongly et al. (1999) and Fontana et al. (2000) yield z that nonlinear and galaxies at z ∼ 5–7di ffer little in ph agree fairly well with each other. Thus, the z values age from those at z ∼ 3–4 (of which ∼103 are ph for HDF-N objects with z =5–7identi fied using the already known). Let us illustrate this point using data of Fontana et al. (2000) differ from the z the Einstein–deSitter model as an example. In this ph model, age t is related to z in the following simple determinations of Fernandez-Soto et al. (1999) by +0.24 ± 0.39 (eight galaxies). 2 − 3 −1 way: t = (1 + z) 2 H ,whereH is the Hubble 3 0 0 The subsequent work was based on the origi- nal I -band frames of the two fields available from constant. It thus follows that for H0 =50km/s/Mpc 814 the present-day (z =0) age of the Universe is equal the site of the Space Telescope Science Institute (STScI). To identify real galaxies, we analyzed sur- to t0 =13.0 Gyr. Galaxies with z =3are observed at t =1.6 Gyr, and those with z =4,att =1.2 Gyr. face brightness distributions for all objects with zph = 5–7. An analysis of the profiles of several dozen stars Redshifts z =5and z =7correspond to the age of the Universe of 0.9 and 0.6 Gyr, respectively. The in these fields showed that they had FWHM =0.14. galaxies at z ∼ 3.5 are therefore “older” than those Note that the width of the stellar profiles depends only observed at z ∼ 6 by no more than 109 yr. Most of the slightly on apparent magnitude: FWHM =0.146 ± time of cosmic evolution falls within z ≤ 1. 0.018 and FWHM =0.139 ± 0.026 for stars with m m To identify objects with z =5–7, we used pub- I814 > 22 and fainter stars with I814 > 24 , respec- lished photometric redshifts zph of objects in HDF-N tively. We left in the final list only the resolvable ob- and HDF-S adopted from the catalogs of Fernandez- jects whose brightness distribution is more extended Soto et al. (1999) and Fontana et al. (2000) (see that those of stars (FWHM > 0.14). the corresponding WWW addresses in the original Tables 1 and 2 list candidate distant galaxies in papers). The zph estimates in the corresponding pa- HDF-N and HDF-S, respectively. The first column pers are based on seven-color (V300 to K) photometry. of Table 1 gives the number of the object according The accuracy of zph is difficult to assess, because to the catalog of Fernandez-Soto et al. (1999); the only several galaxies are now known to have spectro- second column, its name according to Williams et al. scopic z exceeding 5 (see Introduction). However, in (1996); the third column, the apparent I814 magni- HDF-N, two such such objects were classified as tude in the AB system of Oke (1974); the fourth galaxies with z>5 based just on photometric red- column, the spectroscopic redshift (Spinrad et al. shifts, and their zph were subsequently corroborated 1998; Weymann et al. 1998); the fifth column, the through spectroscopic observations (Spinrad et al. photometric redshift zph according to Fontana et al. 1998; Weymann et al. 1998). For these two ob- (2000) and the last column, the spectral type of the jects, the difference between the two redshifts z − zph galaxy (i.e., the spectral type that best describes the amounts to −0.13 ± 0.22 (see Table 1).
Load more

Recommended publications
  • Arxiv:0804.4630V1 [Astro-Ph] 29 Apr 2008 I Ehnv20;Ficao 06) Ti Nti Oeas Role This in Is It 2006A)
    DRAFT VERSION NOVEMBER 9, 2018 Preprint typeset using LATEX style emulateapj v. 05/04/06 OPEN CLUSTERS AS GALACTIC DISK TRACERS: I. PROJECT MOTIVATION, CLUSTER MEMBERSHIP AND BULK THREE-DIMENSIONAL KINEMATICS PETER M. FRINCHABOY1,2,3 AND STEVEN R. MAJEWSKI2 Department of Astronomy, University of Virginia, P.O. Box 400325, Charlottesville, VA 22904-4325, USA Draft version November 9, 2018 ABSTRACT We have begun a survey of the chemical and dynamical properties of the Milky Way disk as traced by open star clusters. In this first contribution, the general goals of our survey are outlined and the strengths and limita- tions of using star clusters as a Galactic disk tracer sample are discussed. We also present medium resolution (R 15,0000) spectroscopy of open cluster stars obtained with the Hydra multi-object spectrographs on the Cerro∼ Tololo Inter-American Observatory 4-m and WIYN 3.5-m telescopes. Here we use these data to deter- mine the radial velocities of 3436 stars in the fields of open clusters within about 3 kpc, with specific attention to stars having proper motions in the Tycho-2 catalog. Additional radial velocity members (without Tycho-2 proper motions) that can be used for future studies of these clusters were also identified. The radial velocities, proper motions, and the angular distance of the stars from cluster center are used to derive cluster member- ship probabilities for stars in each cluster field using a non-parametric approach, and the cluster members so-identified are used, in turn, to derive the reliable bulk three-dimensional motion for 66 of 71 targeted open clusters.
    [Show full text]
  • Magnetic Fronts in Galaxies A
    Astronomy Reports, Vol. 45, No. 7, 2001, pp. 497–501. Translated from AstronomicheskiÏ Zhurnal, Vol. 78, No. 7, 2001, pp. 579–584. Original Russian Text Copyright © 2001 by Petrov, Sokoloff, Moss. Magnetic Fronts in Galaxies A. P. Petrov1, D. D. Sokoloff 2, and D. L. Moss3 1Russian University of Peoples’ Friendship, Moscow, Russia 2Moscow State University, Moscow, Russia 3University of Manchester, Manchester, England Received October 18, 2000 Abstract—Magnetic-field reversals observed in the Milky Way at one or more Galactocentric radii are inter- preted as long-lived transient structures containing memory of the seed magnetic fields. These magnetic fronts can be described using the so-called no-z approximation for the nonlinear, mean-field dynamo equations, which are the topic of the paper. We obtain asymptotic estimates for the speed of propagation of discontinuities in the solution (internal fronts). These estimates agree well with numerical solutions of the no-z equations, and sup- port our interpretation of the magnetic-field reversals as long-lived transients. © 2001 MAIK “Nauka/Interpe- riodica”. 1. INTRODUCTION Such a discussion is the aim of this paper. Based on our analysis, we demonstrate that estimates for the life- The large-scale magnetic fields of spiral galaxies times of a magnetic front obtained in [3] are robust and appear to result from the action of the galactic dynamo, do not depend on the detailed vertical structure of the driven by the differential rotation of the galactic disk and galaxy. the helicity of the interstellar turbulence. The azimuthal component of the galactic magnetic field is dominant. In the Milky Way, however, the azimuthal component 2.
    [Show full text]
  • Astro-Ph/0107318V1 17 Jul 2001 1562
    The Unique Type Ia Supernova 2000cx in NGC 524 Weidong Li1, Alexei V. Filippenko1, Elinor Gates2, Ryan Chornock1, Avishay Gal-Yam3,4, Eran O. Ofek3, Douglas C. Leonard5, Maryam Modjaz1, R. Michael Rich6, Adam G. Riess7, and Richard R. Treffers1 Email: [email protected], [email protected], [email protected] Received ; accepted arXiv:astro-ph/0107318v1 17 Jul 2001 1Department of Astronomy, University of California, Berkeley, CA 94720-3411. 2Lick Observatory, PO Box 82, Mount Hamilton, CA 95140. 3School of Physics and Astronomy, and the Wise Observatory, Tel Aviv University, Israel. 4Colton Fellow. 5Five College Astronomy Department, University of Massachusetts, Amherst, MA 01003- 9305. 6Department of Physics and Astronomy, University of California, Los Angeles, CA 90095- 1562. 7Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218. –2– ABSTRACT We present extensive photometric and spectroscopic observations of the Type Ia supernova (SN Ia) 2000cx in the S0 galaxy NGC 524, which reveal it to be peculiar. Photometrically, SN 2000cx is different from all known SNe Ia, and its light curves cannot be fit well by the fitting techniques currently available. There is an apparent asymmetry in the B-band peak, in which the premaximum brightening is relatively fast (similar to that of the normal SN 1994D), but the postmaximum decline is relatively slow (similar to that of the overluminous SN 1991T). The color evolution of SN 2000cx is also peculiar: the (B − V )0 color has a unique plateau phase and the (V − R)0 and (V − I)0 colors are very blue. Although the premaximum spectra of SN 2000cx are similar to those of SN 1991T-like objects (with weak Si II lines), its overall spectral evolution is quite different.
    [Show full text]
  • The Peculiar Motions of Early-Type Galaxies in Two Distant Regions VII
    Mon. Not. R. Astron. Soc. 321, 277±305 (2001) The peculiar motions of early-type galaxies in two distant regions ± VII. Peculiar velocities and bulk motions Matthew Colless,1w R. P. Saglia,2 David Burstein,3 Roger L. Davies,4 Robert K. McMahan, Jr5 and Gary Wegner6 1Research School of Astronomy & Astrophysics, The Australian National University, Weston Creek, Canberra, ACT 2611, Australia 2Institut fuÈr Astronomie und Astrophysik, Scheinerstraûe 1, D-81679 Munich, Germany 3Department of Physics and Astronomy, Arizona State University, Tempe, AZ 85287-1504, USA 4Department of Physics, University of Durham, South Road, Durham DH1 3LE 5Department of Physics and Astronomy, University of North Carolina, CB#3255 Phillips Hall, Chapel Hill, NC 27599-3255, USA 6Department of Physics and Astronomy, Dartmouth College, Wilder Lab, Hanover, NH 03755, USA Accepted 2000 August 31. Received 2000 August 31; in original form 2000 May 23 ABSTRACT We present peculiar velocities for 85 clusters of galaxies in two large volumes at distances between 6000 and 15 000 km s21 in the directions of Hercules±Corona Borealis and Perseus±Pisces±Cetus (the EFAR sample). These velocities are based on Fundamental Plane (FP) distance estimates for early-type galaxies in each cluster. We fit the FP using a maximum likelihood algorithm which accounts for both selection effects and measurement errors, and yields FP parameters with smaller bias and variance than other fitting procedures. We obtain a best-fitting FP with coefficients consistent with the best existing determinations. We measure the bulk motions of the sample volumes using the 50 clusters with the best- determined peculiar velocities.
    [Show full text]
  • Astroparticle Physics at LHC
    MSc Physics Master Thesis Astroparticle physics at LHC Dark matter search in ATLAS by Michaël Muusse 6171885 September 2015 60 EC September 2013 – September 2015 Supervisor/Examiner: Examiner: Dr. D. Berge Dr. M. Vreeswijk ... Astroparticle physics at the LHC Dark matter search in ATLAS Astrophysics at the LHC – Dark matter seach in ATLAS ii Astrophysics at the LHC – Dark matter seach in ATLAS iii Astroparticle physics at the LHC Dark matter search in ATLAS Master thesis in Physics Michael Muusse July 2015 Track: Grappa, University of Amsterdam Supervisor: Dr. D. Berge 2nd supervisor: Dr. D. Salek Second Reviewer: Dr. M. Vreeswijk ... Astrophysics at the LHC – Dark matter seach in ATLAS iv Front cover image credit: [14] [178] edited. Astrophysics at the LHC – Dark matter seach in ATLAS v Abstract Astroparticle physics at the LHC – Dark matter search in ATLAS In astronomy and cosmology the hypothesized existence of dark matter and its properties are inferred indirectly from observed gravitational effects. An explanation for the missing mass problem in the study of motion of galaxies and clusters, the shape of galactic rotation curves, observations on weak gravitational lens effects near clusters and the correspondence between the cosmic microwave background anisotropies and the large- scale structure of the Universe, could be given by a form of non electromagnetic interacting, invisible matter, hence called dark matter. An undetected heavy elementary relic particle that interacts only trough the gravitational and weak forces is a leading candidate for dark matter. Furthermore elementary particles with Weakly Interacting Massive Particle (WIMP) properties arise often in theories beyond the standard model.
    [Show full text]
  • Peg – Objektauswahl NGC Teil 1
    Peg – Objektauswahl NGC Teil 1 NGC 0001 NGC 0042 NGC 7074 NGC 7146 NGC 7206 NGC 7270 NGC 7303 NGC 7321 NGC 0002 NGC 0052 NGC 7078 NGC 7147 NGC 7207 NGC 7271 NGC 7305 NGC 7323 NGC 0009 NGC 7033 NGC 7085 NGC 7149 NGC 7212 NGC 7272 NGC 7311 NGC 7324 NGC 0014 NGC 7034 NGC 7094 NGC 7156 NGC 7217 NGC 7275 NGC 7312 NGC 7328 Teil 2 NGC 0015 NGC 7042 NGC 7101 NGC 7159 NGC 7224 NGC 7280 NGC 7315 NGC 7331 NGC 0016 NGC 7043 NGC 7102 NGC 7177 NGC 7236 NGC 7283 NGC 7316 NGC 7332 Teil 3 NGC 0022 NGC 7053 NGC 7113 NGC 7190 NGC 7237 NGC 7286 NGC 7317 NGC 7335 NGC 0023 NGC 7056 NGC 7132 NGC 7193 NGC 7241 NGC 7290 NGC 7318 NGC 7336 Teil 4 NGC 0026 NGC 7066 NGC 7137 NGC 7194 NGC 7244 NGC 7291 NGC 7319 NGC 7337 NGC 0041 NGC 7068 NGC 7138 NGC 7195 NGC 7253 NGC 7292 NGC 7320 NGC 7339 Sternbild- Zur Objektauswahl: Nummer anklicken Übersicht Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Zum Detailfoto: Objekt in Übersichtskarte anklicken Peg – Objektauswahl NGC Teil 2 NGC 7340 NGC 7360 NGC 7375 NGC 7411 NGC 7435 NGC 7463 NGC 7479 NGC 7509 Teil 1 NGC 7342 NGC 7362 NGC 7376 NGC 7413 NGC 7436 NGC 7464 NGC 7485 NGC 7511 NGC 7343 NGC 7363 NGC 7383 NGC 7414 NGC 7437 NGC 7465 NGC 7487 NGC 7512 NGC 7345 NGC 7366 NGC 7385 NGC 7415 NGC 7439 NGC 7466 NGC 7489 NGC 7514 NGC 7346 NGC 7367 NGC 7386 NGC 7420 NGC 7442 NGC 7467 NGC 7490 NGC 7515 NGC 7347 NGC 7369 NGC 7387 NGC 7427 NGC 7448 NGC 7468 NGC 7495 NGC 7516 Teil 3 NGC 7348 NGC 7370 NGC 7389 NGC 7430 NGC 7451 NGC 7469 NGC 7497 NGC 7519 NGC 7353 NGC 7372 NGC 7390 NGC 7431 NGC 7454 NGC 7473 NGC 7500 NGC 7523 Teil
    [Show full text]
  • The Dichotomy of Seyfert 2 Galaxies: Intrinsic Differences and Evolution
    A&A 570, A72 (2014) Astronomy DOI: 10.1051/0004-6361/201424622 & c ESO 2014 Astrophysics The dichotomy of Seyfert 2 galaxies: intrinsic differences and evolution E. Koulouridis Institute for Astronomy and Astrophysics, Space Applications and Remote Sensing, National Observatory of Athens, 15236 Palaia Penteli Athens, Greece e-mail: [email protected] Received 17 July 2014 / Accepted 20 August 2014 ABSTRACT We present a study of the local environment (≤200 h−1 kpc) of 31 hidden broad line region (HBLR) and 43 non-HBLR Seyfert 2 (Sy2) galaxies in the nearby universe (z ≤ 0.04). To compare our findings, we constructed two control samples that match the redshift and the morphological type distribution of the HBLR and non-HBLR samples. We used the NASA Extragalactic Database (NED) to find all neighboring galaxies within a projected radius of 200 h−1 kpc around each galaxy, and a radial velocity difference δu ≤ 500 km s−1. Using the digitized Schmidt survey plates (DSS) and/or the Sloan Digital Sky Survey (SDSS), when available, we confirmed that our sample of Seyfert companions is complete. We find that, within a projected radius of at least 150 h−1 kpc around each Seyfert, the fraction of non-HBLR Sy2 galaxies with a close companion is significantly higher than that of their control sample, at the 96% confidence level. Interestingly, the difference is due to the high frequency of mergers in the non-HBLR sample, seven versus only one in the control sample, while they also present a high number of hosts with signs of peculiar morphology.
    [Show full text]
  • I. INTRODUCTION This Report Covers Astronomical Activities Primarily
    I. INTRODUCTION meeting of the Astronomical Society of the Pacific - "Universe '95" from June 22 through 28. The public program drew over This report covers astronomical activities primarily 1000 persons during a weekend of talks and exhibits. This was within Maryland's Department of Astronomy but also includes preceded by a teachers' workshop - "Universe in the some astronomical work carried out in other departments, such Classroom". As part of the overall proceedings, J. Percy (U. of as the Department of Physics. The period covered is from 1 Toronto) organized an Astronomy Education Symposium: October 1994 through 30 September 1995. "Current Developments, Future Coordination" which was attended by approximately 200 educators. V. Trimble II. PERSONNEL organized the Scientific Symposium: "Clusters, Lensing and the Future of the Universe" which had over 100 scientists The continuing personnel in the Department of participating. Local organizing for the various events was Astronomy during the period were Professors M. Leventhal done by D. Wentzel and J. Trasco. (Chair), M. F. A'Hearn, R. A. Bell, L. Blitz, J. P. Harrington, M. R. Kundu, K. Papadopoulos, W. K. Rose, V. L. Trimble, IV. FACILITIES AND INSTRUMENTATION and A. S. Wilson; Emeritus Professors W. C. Erickson, F. J. Kerr, and D. G. Wentzel; Adjunct Professors M. Hauser and S. A. Laboratory for Millimeter-Wave Astronomy Holt; Associate Professors L. G. Mundy and S. Vogel; Visiting Associate Professors L. McFadden and S. Vrtilek; The LMA is the organization set up by the University of Assistant Professors J. Stone, J. Wang, and S. Veilleux; Maryland to manage its participation in the Berkeley-Illinois- Associate Research Scientists C.
    [Show full text]
  • Personnel Elected Representative to the CPTS Directors, Scientific Members Dr
    Dr. Brian Reville, from 01.05. 2019 Personnel Elected Representative to the CPTS Directors, Scientific Members Dr. Bernhard Schwingenheuer Prof. Dr. Klaus Blaum – stored and cooled ions The following list includes persons working at the Prof. Dr. Jim A. Hinton – non-thermal astrophysics institute during all or part of the reporting period. All Prof. Dr. Werner Hofmann – particle physics and high- persons are listed in their last/present energy astrophysics, until 31.05.2019 position.Scientific Staff Honorarprof. Dr. Christoph H. Keitel – theoretical quantum dynamics and quantum electrodynamics Prof. Dr. Evgeny Akhmedov Prof. Dr. Dr. h.c. Manfred Lindner – particle and Dr. Christian Bauer astroparticle physics PD Dr. Konrad Bernlöhr Prof. Dr. Thomas Pfeifer – quantum dynamics and Dr. Christian Buck control PD Dr. José Ramón Crespo López-Urrutia PD Dr. Antonino Di Piazza Emeriti Scientific Members PD Dr. Alexander Dorn Prof. Dr. Hugo Fechtig Dr. Sergey Eliseev Prof. Dr. Werner Hofmann apl. Prof. Dr. Jörg Evers Prof. Dr. Konrad Mauersberger PD Dr. Bernold Feuerstein Prof. Dr. Bogdan Povh Dr. Manfred Grieser Prof. Dr. Heinrich J. Völk Dr. Robert von Hahn Prof. Dr. Hans-Arwed Weidenmüller Prof. Dr. Wolfgang Hampel PD Dr. Zoltán Harman External Scientific Members Dr. habil. Karen Z. Hatsagortsyan Dr. German Hermann Prof. Dr. Felix A. Aharonian, Dublin Dr. Rebecca Hermkes Prof. Dr. Rudolf M. Bock, Darmstadt Dr. Gerd Heusser Prof. Dr. Stanley J. Brodsky, Stanford Dr. Gertrud Hönes Prof. Dr. Lorenz S. Cederbaum, Heidelberg Prof. Dr. John Kirk Prof. Dr. Johannes Geiss, Bern Prof. Dr. Till Kirsten Prof. Dr. Gisbert Frhr. zu Putlitz, Heidelberg Prof. Dr. Karl Tasso Knöpfle Prof.
    [Show full text]
  • SFI++. II. a NEW I-BAND TULLY-FISHER CATALOG, DERIVATION of PECULIAR VELOCITIES, and DATA SET PROPERTIES Christopher M
    The Astrophysical Journal Supplement Series, 172:599Y614, 2007 October A # 2007. The American Astronomical Society. All rights reserved. Printed in U.S.A. SFI++. II. A NEW I-BAND TULLY-FISHER CATALOG, DERIVATION OF PECULIAR VELOCITIES, AND DATA SET PROPERTIES Christopher M. Springob,1,2,3 Karen L. Masters,4,3 Martha P. Haynes,3,5 Riccardo Giovanelli,3,5 and Christian Marinoni6 Received 2006 September 1; accepted 2007 April 18 ABSTRACT We present the SFI++ data set, a homogeneously derived catalog of photometric and rotational properties and the Tully-Fisher distances and peculiar velocities derived from them. We make use of digital optical images, optical long- slit spectra, and global H i line profiles to extract parameters of relevance to disk scaling relations, incorporating several previously published data sets as well as a new photometric sample of some 2000 objects. According to the completeness of available redshift samples over the sky area, we exploit both a modified percolation algorithm and the Voronoi-Delaunay method to assign individual galaxies to groups as well as clusters, thereby reducing scatter in- troduced by local orbital motions. We also provide corrections to the peculiar velocities for both homogeneous and inhomogeneous Malmquist bias, making use of the 2MASS Redshift Survey density field to approximate large-scale structure. We summarize the sample selection criteria, corrections made to raw observational parameters, the grouping techniques, and our procedure for deriving peculiar velocities. The final SFI++ peculiar velocity catalog of 4861 field and cluster galaxies is large enough to permit the study not just of the global statistics of large-scale flows but also of the details of the local velocity field.
    [Show full text]
  • DSO List V2 Current
    7000 DSO List (sorted by constellation - magnitude) 7000 DSO List (sorted by constellation - magnitude) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs SAC NOTES M 31 NGC 224 Galaxy AND 3.4 13.5 189' 00 42.7 +41 16 60 Sb Andromeda Galaxy;Local Group;nearest spiral NGC 7686 OCL 251 Opn CL AND 5.6 - 15' 23 30.1 +49 08 88 IV 1 p 20 6.2 H VIII 69;12* mags 8...13 NGC 752 OCL 363 Opn CL AND 5.7 - 50' 01 57.7 +37 40 92 III 1 m 60 9 H VII 32;Best in RFT or binocs;Ir scattered cl 70* m 8... M 32 NGC 221 Galaxy AND 8.1 12.4 8.5' 00 42.7 +40 52 60 E2 Companion to M31; Member of Local Group M 110 NGC 205 Galaxy AND 8.1 14 19.5' 00 40.4 +41 41 60 SA0 M31 Companion;UGC 426; Member Local Group NGC 272 OCL 312 Opn CL AND 8.5 - 00 51.4 +35 49 90 IV 1 p 8 9 NGC 7662 PK 106-17.1 Pln Neb AND 8.6 5.6 17'' 23 25.9 +42 32 88 4(3) 14 Blue Snowball Nebula;H IV 18;Barnard-cent * variable? NGC 956 OCL 377 Opn CL AND 8.9 - 8' 02 32.5 +44 36 62 IV 1 p 30 9 NGC 891 UGC 1831 Galaxy AND 9.9 13.6 13.1' 02 22.6 +42 21 62 Sb NGC 1023 group;Lord Rosse drawing shows dark lane NGC 404 UGC 718 Galaxy AND 10.3 12.8 4.3' 01 09.4 +35 43 91 E0 Mirach's ghost H II 224;UGC 718;Beta AND sf 6' IC 239 UGC 2080 Galaxy AND 11.1 14.2 4.6' 02 36.5 +38 58 93 SBa In NGC 1023 group;vsBN in smooth bar;low surface br NGC 812 UGC 1598 Galaxy AND 11.2 12.8 3' 02 06.9 +44 34 62 Sbc Peculiar NGC 7640 UGC 12554 Galaxy AND 11.3 14.5 10' 23 22.1 +40 51 88 SBbc H II 600;nearly edge on spiral MCG +08-01-016 Galaxy AND 12 - 1.0' 23 59.2 +46 53 59 Face On MCG +08-01-018
    [Show full text]
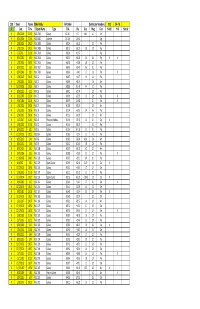
  • MX Date Time Object Name Type RA Dec Size Mag Con H-400 H-II
    2382 : Count Name: Mike Hotka RA Order Certificate Numbers: 303 54 - M X Date Time Object Name Type R.A. Dec Size Mag Con H-400 H-II Hustle X 3/31/2019 21:53 NGC 4366 Galaxy 12:24.5 +7.3 .9x.6 14.3 Vir X 9/24/2016 21:34 NGC 6561 Asterism 18:10.5 -16:43 Sgr X 1/18/2015 20:23 NGC 7805 Galaxy 0:01.4 +31:26 13.3 Peg X 1/18/2015 20:23 NGC 7806 Galaxy 0:01.5 +31:27 1.9 13.5 Peg X 1/7/2012 21:09 NGC 7810 Galaxy 0:02.4 +12:57 Peg X 8/11/2002 0:56 NGC 7814 Galaxy 0:03.3 +16:09 2.6 10.6 Peg X X X 1/18/2015 20:55 NGC 7816 Galaxy 0:03.8 +7:28 1.8 12.8 Psc X 8/19/2012 1:16 NGC 7817 Galaxy 0:04.0 +20:45 4.6 11.8 Peg X 9/30/2006 0:50 NGC 7832 Galaxy 0:06.6 -3:42 1.7 13.8 Psc X X 1/18/2015 20:05 NGC 12 Galaxy 0:08.7 +4:37 1.9 14.1 Psc X 1/18/2005 20:26 NGC 13 Galaxy 0:08.8 +33:26 13.6 And X 10/27/2008 19:55 NGC 14 Galaxy 0:08.8 +15:49 4.4 12.1 Peg X 8/19/2012 1:12 NGC 16 Galaxy 0:09.1 +27:44 12.0 Peg X 9/19/2006 23:06 NGC 23 Galaxy 0:09.9 +25:55 2.3 12.0 Peg X X 9/19/2006 23:18 NGC 24 Galaxy 0:09.9 -24:58 11.5 Scl X X 1/18/2015 20:28 NGC 29 Galaxy 0:10.8 +33:21 12.6 And X 1/18/2015 20:06 NGC 36 Galaxy 0:11.4 +6:23 2.4 14.4 Psc X 1/18/2015 20:30 NGC 39 Galaxy 0:12.3 +31:03 13.5 And X 11/2/2007 21:45 NGC 40 Planetary Nebula 0:13.0 +72:32 0.3 10.7 Cep X X 1/18/2015 21:16 NGC 52 Galaxy 0:14.6 +18:33 13.3 Peg X 8/19/2012 3:01 NGC 57 Galaxy 0:15.4 +17:18 4.1 11.6 Psc X 12/27/2013 18:21 NGC 61A Galaxy 0:16.5 -6:14 1.1 14.7 Psc X 8/19/2012 1:44 NGC 68 Galaxy 0:18.3 +30:04 62.0 13.0 And X 8/19/2012 2:58 NGC 95 Galaxy 0:22.2 +10:30 7.8 12.6 Psc X 8/19/2012 1:41
    [Show full text]