DOCSLIB.ORG

Magnetic Fronts in Galaxies A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Magnetic Fronts in Galaxies A Astronomy Reports, Vol. 45, No. 7, 2001, pp. 497–501. Translated from AstronomicheskiÏ Zhurnal, Vol. 78, No. 7, 2001, pp. 579–584. Original Russian Text Copyright © 2001 by Petrov, Sokoloff, Moss. Magnetic Fronts in Galaxies A. P. Petrov1, D. D. Sokoloff 2, and D. L. Moss3 1Russian University of Peoples’ Friendship, Moscow, Russia 2Moscow State University, Moscow, Russia 3University of Manchester, Manchester, England Received October 18, 2000 Abstract—Magnetic-field reversals observed in the Milky Way at one or more Galactocentric radii are inter- preted as long-lived transient structures containing memory of the seed magnetic fields. These magnetic fronts can be described using the so-called no-z approximation for the nonlinear, mean-field dynamo equations, which are the topic of the paper. We obtain asymptotic estimates for the speed of propagation of discontinuities in the solution (internal fronts). These estimates agree well with numerical solutions of the no-z equations, and sup- port our interpretation of the magnetic-field reversals as long-lived transients. © 2001 MAIK “Nauka/Interpe- riodica”. 1. INTRODUCTION Such a discussion is the aim of this paper. Based on our analysis, we demonstrate that estimates for the life- The large-scale magnetic fields of spiral galaxies times of a magnetic front obtained in [3] are robust and appear to result from the action of the galactic dynamo, do not depend on the detailed vertical structure of the driven by the differential rotation of the galactic disk and galaxy. the helicity of the interstellar turbulence. The azimuthal component of the galactic magnetic field is dominant. In the Milky Way, however, the azimuthal component 2. EQUATIONS, GENERATION MECHANISM, reverses between the Orion and Sagittarius arms, and AND EQUILIBRIUM SOLUTION there may be additional reversals ([1], see [2] for a dis- cussion of the current state of this problem and the pos- We consider a galactic disk of radius R and uniform sibility of observing reversals in external galaxies). semi-thickness h. The equations of the no-z model for the azimuthal (Bφ) and radial (B ) components of an One possible explanation of the field reversals is the r following. Let us suppose that, by chance, the seed mag- axisymmetric magnetic field averaged over the vertical netic field has a reversal somewhere between Galactocen- cross section of the galactic disk are tric radii r and r . In the nonlinear stage of magnetic-field ∂ 1 2 Br 2 ∂ 1 ∂ evolution, a magnetic front with sharp field reversals -------- = – Rαα()B Bφ – B + λ ----- -------- ()rB , ∂t r ∂r r ∂r r appears somewhere between r1 and r˙2 . We identify the (1) ∂ front with this reversal. The front moves slowly in the Bφ 2 ∂ 1 ∂ --------- = RωGB – Bφ + λ ----- -------- ()rBφ . Galactic disk, and the estimates of [3] show that its life- ∂t r ∂r r ∂r time can be on the order of the age of the Galaxy. ∂Ω ∂ Ω However, some of the estimates in [3] require Here, G = r / r, where (r) is the rotation law, α η Ω 2 η detailed information about the vertical structure of the Rα = 0h/ and Rω = 0h / are dimensionless num- Galactic disk, while observations mainly provide infor- bers specifying the amplitudes of the helicity and dif- α Ω mation about the properties of the magnetic field and ferential rotation, respectively, where 0 and 0 are turbulence averaged over a vertical cross section of the representative values of α and Ω, and λ = h/R is the disk disk. Fortunately, the galactic dynamo equations can be aspect ratio. The ÐBr and ÐBφ terms in the first and sec- presented in a form known as the no-z model, which ond equations of (1) approximate the (dominant) diffu- focuses attention on the field structure in the galactic sion term perpendicular to the galactic disk. We allow plane and ignores structure in the vertical direction ([4], the dynamo to be saturated via α quenching: see also [5]). α() α() α()2 The no-z model appears to be very robust and quite B ==Bφ 0 fgBφ , (2) adequate for making comparisons with most observa- α 2 tions (see [6]). However, until now, it has been consid- where 0 is chosen such that f(0) = 1, g = 1/B0 , and B0 ered in the context of the particular physical problem of is the characteristic magnetic-field strength at which the galactic dynamo (see e.g. [3, 5]), and its mathemat- nonlinear effects in the dynamo become important. ical properties have not been discussed systematically. More generally, as in Eqs. (1), α will depend on the 1063-7729/01/4507-0497 $21.00 © 2001 MAIK “Nauka/Interperiodica” 498 PETROV et al. Br here, the ÐBr and ÐBφ terms in (3) are each multiplied π2 ≈ by /4, and so Dcrit 6. L2 A one-component asymptotic analysis ([7], see also S [3, 9]) supposes that the field has the form Ð (), Γt () () (), Γt () M Br tr ==e Qrbr r , Bφ rt e Qrb, (5) L where Q(r) can be obtained by solving the equation 1 M0 Bφ 2 1 ' ΓQ = γ ()r Q + λ ---()rQ ' , (6) r which coincides with the asymptotic expansion in [7]. T1 + M In the nonlinear generalization of (6) [10], γ(r) is replaced by the nonlinear term γ(r, Q). In contrast, deal- ing with the no-z model, we introduce nonlinearity into T2 Eqs. (1) directly. We now turn to the nonlinear properties of the The phase plane of the dynamical system (3): trajectories no-z model. Let us consider the steady-state problem are attracted to the states M+ and MÐ (for notation, see the for Eqs. (3): text). α ()2 Rα 0 fgBφ Bφ +0,Br ==RωGBr –0.Bφ (7) strength of the total field B, but for analytical conve- Equations (7) has the trivial solution Br = 0, Bφ = 0 αω 0 nience we take the simpler form (2). In the approx- (denoted below as M in the (Bφ, B ) plane) and, if the | | ≈ r imation (used here), B Bφ, and the differences magnetic-field generation is strong enough, there are between these forms for α quenching are small. The two nontrivial solutions: 2 function f is usually thought to decay with Bφ , to pro- () () ± ± kr ± ± 1 kr vide negative feedback on the magnetic-field genera- Bφ ==----------() , Br ----------- ----------() , tion. gr RωG gr If the seed magnetic field is sufficiently smooth and denoted below as M±. Here, k(r) means the nonvanish- remains smooth during the subsequent field evolution, ing positive root of the equation the radial diffusion terms in Eqs. (1) can be neglected, α ()2 yielding 1 +0DG 0 fgBφ = (8) (if the root does not exist, then neither do the nontrivial dBr α ()2 --------- = – Rα 0 fgBφ Bφ – Br, solutions; if several roots exist, we mean the smallest dt (3) one). dBφ ± ± --------- = RωGB – Bφ. If the solutions Bφ , B exist, then they are stable dt r r 0 0 and the solution Bφ , B is unstable. If, as usual, G < 0, Note that r can be considered a parameter in Eqs. (3). r Bφ and Br for the nontrivial equilibrium solution have We begin with the kinematic problem, neglecting opposite signs. nonlinear terms and looking for a separable solution of γt γt For the supercritical dynamo, direct calculation the form B (r, t) = b (r)e , Bφ = be . This eigenvalue r r shows that M0 is a saddle point, and M± are stable focal problem has the solution |α | |α | ≤ points if 0DG > 2 or stable nodal points if 0DG 2. γ ()r ==– 1 + –,Dα G br() γ ()r , Thus, the solution for the field tends to a stable point 0 (4) through oscillatory states if the field generation is () α br r = Rα 0. strong enough and monotonically if the generation is weaker. The excitation conditions are G < 0 and D > D = cr We present in the figure the phase portrait for Eqs. (3) α Ð1 min( 0G) , which is in qualitative agreement with the for the oscillatory case. The curves L , L represent the corresponding result for the complete mean-field equa- 1 2 ≈ − α 2 1 tions, namely Dcr 8 (e.g., [7]). Phillips [8] established functions Br = Rα 0f(gBφ )Bφ, Br = ----------- Bφ, respec- a close correspondence between no-z and asymptotic RωG solutions, and suggested a correction factor to be tively. The trajectories of system (3) are vertical when inserted in the no-z formulation that largely removes crossing the curve L2 and horizontal when crossing the the quantitative disagreement. If we insert this factor curve L1. Some typical trajectories are denoted T1 and T2. ASTRONOMY REPORTS Vol. 45 No. 7 2001 MAGNETIC FRONTS IN GALAXIES 499 τ λ The trajectories in the “southeast” (“northwest”) half- Here, = (r Ð r0)/ is a stretched variable and r0 is a sta- plane are attracted to M1 (M2). The separatrix S is given by ble reversal point (terms up to order λ are presented). 2 The smooth part of expansion (14) approximates the dB Rαα gBφ Bφ + B | | λ0 ---------r = ----------------------------------------0 r , (9) solution where r Ð r0 ~ , while the boundary func- dBφ – RωGBr + Bφ tions are introduced to make the expansion valid when ≈ r r0. The boundary functions must decrease rapidly with the initial conditions B = 0, Bφ = 0 (more accu- r (usually exponentially). rately, B 0 when Bφ 0). r Substituting (14) into (12) and equating terms of The solution of (9) for small B and Bφ—i.e., for a r order λ0, we obtain u = v = ±1, or u = v = 0. For weak seed field—is given by 0 0 0 0 a front solution, we set u = v = –1 for r < r and α 0 0 0 Rα 0 u = v = 1 for r > r .
Load more

Recommended publications
  • Progressive Redshifts in the Late-Time Spectra of Type IA Supernovae
    Dartmouth College Dartmouth Digital Commons Dartmouth Scholarship Faculty Work 8-9-2016 Progressive Redshifts in the Late-Time Spectra of Type IA Supernovae C. S. Black Dartmouth College R. A. Fesen Dartmouth College J. T. Parrent Harvard-Smithsonian Center for Astrophysics Follow this and additional works at: https://digitalcommons.dartmouth.edu/facoa Part of the Astrophysics and Astronomy Commons Dartmouth Digital Commons Citation Black, C. S.; Fesen, R. A.; and Parrent, J. T., "Progressive Redshifts in the Late-Time Spectra of Type IA Supernovae" (2016). Dartmouth Scholarship. 1806. https://digitalcommons.dartmouth.edu/facoa/1806 This Article is brought to you for free and open access by the Faculty Work at Dartmouth Digital Commons. It has been accepted for inclusion in Dartmouth Scholarship by an authorized administrator of Dartmouth Digital Commons. For more information, please contact [email protected]. DRAFT VERSION AUGUST 9, 2016 Preprint typeset using LATEX style emulateapj v. 5/2/11 PROGRESSIVE RED SHIFTS IN THE LATE-TIME SPECTRA OF TYPE IA SUPERNOVAE C. S. BLACK1 , R. A. FESEN1 , & J. T. PARRENT2 16127 Wilder Lab, Department of Physics & Astronomy, Dartmouth College, Hanover, NH 03755 and 2Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA Draft version August 9, 2016 ABSTRACT We examine the evolution of late-time, optical nebular features of Type Ia supernovae (SNe Ia) using a sample consisting of 160 spectra of 27 normal SNe Ia taken from the literature as well as unpublished spectra of SN 2008Q and ASASSN-14lp. Particular attention was given to nebular features between 4000-6000 Å in terms of temporal changes in width and central wavelength.
    [Show full text]
  • Copyright by Robert Michael Quimby 2006 the Dissertation Committee for Robert Michael Quimby Certifies That This Is the Approved Version of the Following Dissertation
    Copyright by Robert Michael Quimby 2006 The Dissertation Committee for Robert Michael Quimby certifies that this is the approved version of the following dissertation: The Texas Supernova Search Committee: J. Craig Wheeler, Supervisor Peter H¨oflich Carl Akerlof Gary Hill Pawan Kumar Edward L. Robinson The Texas Supernova Search by Robert Michael Quimby, A.B., M.A. DISSERTATION Presented to the Faculty of the Graduate School of The University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of DOCTOR OF PHILOSOPHY THE UNIVERSITY OF TEXAS AT AUSTIN December 2006 Acknowledgments I would like to thank J. Craig Wheeler, Pawan Kumar, Gary Hill, Peter H¨oflich, Rob Robinson and Christopher Gerardy for their support and advice that led to the realization of this project and greatly improved its quality. Carl Akerlof, Don Smith, and Eli Rykoff labored to install and maintain the ROTSE-IIIb telescope with help from David Doss, making this project possi- ble. Finally, I thank Greg Aldering, Saul Perlmutter, Robert Knop, Michael Wood-Vasey, and the Supernova Cosmology Project for lending me their image subtraction code and assisting me with its installation. iv The Texas Supernova Search Publication No. Robert Michael Quimby, Ph.D. The University of Texas at Austin, 2006 Supervisor: J. Craig Wheeler Supernovae (SNe) are popular tools to explore the cosmological expan- sion of the Universe owing to their bright peak magnitudes and reasonably high rates; however, even the relatively homogeneous Type Ia supernovae are not intrinsically perfect standard candles. Their absolute peak brightness must be established by corrections that have been largely empirical.
    [Show full text]
  • Arxiv:0804.4630V1 [Astro-Ph] 29 Apr 2008 I Ehnv20;Ficao 06) Ti Nti Oeas Role This in Is It 2006A)
    DRAFT VERSION NOVEMBER 9, 2018 Preprint typeset using LATEX style emulateapj v. 05/04/06 OPEN CLUSTERS AS GALACTIC DISK TRACERS: I. PROJECT MOTIVATION, CLUSTER MEMBERSHIP AND BULK THREE-DIMENSIONAL KINEMATICS PETER M. FRINCHABOY1,2,3 AND STEVEN R. MAJEWSKI2 Department of Astronomy, University of Virginia, P.O. Box 400325, Charlottesville, VA 22904-4325, USA Draft version November 9, 2018 ABSTRACT We have begun a survey of the chemical and dynamical properties of the Milky Way disk as traced by open star clusters. In this first contribution, the general goals of our survey are outlined and the strengths and limita- tions of using star clusters as a Galactic disk tracer sample are discussed. We also present medium resolution (R 15,0000) spectroscopy of open cluster stars obtained with the Hydra multi-object spectrographs on the Cerro∼ Tololo Inter-American Observatory 4-m and WIYN 3.5-m telescopes. Here we use these data to deter- mine the radial velocities of 3436 stars in the fields of open clusters within about 3 kpc, with specific attention to stars having proper motions in the Tycho-2 catalog. Additional radial velocity members (without Tycho-2 proper motions) that can be used for future studies of these clusters were also identified. The radial velocities, proper motions, and the angular distance of the stars from cluster center are used to derive cluster member- ship probabilities for stars in each cluster field using a non-parametric approach, and the cluster members so-identified are used, in turn, to derive the reliable bulk three-dimensional motion for 66 of 71 targeted open clusters.
    [Show full text]
  • Virgo the Virgin
    Virgo the Virgin Virgo is one of the constellations of the zodiac, the group tion Virgo itself. There is also the connection here with of 12 constellations that lies on the ecliptic plane defined “The Scales of Justice” and the sign Libra which lies next by the planets orbital orientation around the Sun. Virgo is to Virgo in the Zodiac. The study of astronomy had a one of the original 48 constellations charted by Ptolemy. practical “time keeping” aspect in the cultures of ancient It is the largest constellation of the Zodiac and the sec- history and as the stars of Virgo appeared before sunrise ond - largest constellation after Hydra. Virgo is bordered by late in the northern summer, many cultures linked this the constellations of Bootes, Coma Berenices, Leo, Crater, asterism with crops, harvest and fecundity. Corvus, Hydra, Libra and Serpens Caput. The constella- tion of Virgo is highly populated with galaxies and there Virgo is usually depicted with angel - like wings, with an are several galaxy clusters located within its boundaries, ear of wheat in her left hand, marked by the bright star each of which is home to hundreds or even thousands of Spica, which is Latin for “ear of grain”, and a tall blade of galaxies. The accepted abbreviation when enumerating grass, or a palm frond, in her right hand. Spica will be objects within the constellation is Vir, the genitive form is important for us in navigating Virgo in the modern night Virginis and meteor showers that appear to originate from sky. Spica was most likely the star that helped the Greek Virgo are called Virginids.
    [Show full text]
  • Chilean Senate Ratifies Agreement with ESO Riccardo Giacconi, Director General of ESO
    No. 85 – September 1996 Chilean Senate Ratifies Agreement with ESO Riccardo Giacconi, Director General of ESO On 5 September 1996, the Senate within up to 10 per cent of observing government in direct negotiation with of the Republic of Chile (Second time on all present and future ESO the private claimants. Chamber of the Parliament) approved telescopes in Chile. They also will As part of this Agreement ESO will the Interpretative, Supplementary and have membership on all ESO scien- continue and increase its contributions Modifying Agreement to the Conven- tific and technical committees. Chile- to the development of Chilean astrono- tion of 1963, which regulates the rela- an and European scientific communi- my and the educational and cultural tions between the European Southern ties will henceforth share the impor- development of local communities. Observatory and its host country, the tant scientific discoveries which will ESO is indebted to the Government of Republic of Chile. be made with the VLT facility at Cerro Chile and especially to the Minister of Following formal approval by the Paranal. Foreign Relations, Don José Miguel ESO Council, it is expected that in- By this Agreement the ESO regula- Insulza, and all those who have struments of ratification could be ex- tions for local Chilean staff will be worked towards this Agreement and its changed before the end of this year. modified to incorporate the principles ratification by the Chilean Parliament. The completion of this process is a of Chilean legislation regarding collec- I wish also to recognise the contri- reason for great mutual satisfaction tive bargaining and freedom of associ- bution of all those at ESO who played as the new Agreement consolidates ation.
    [Show full text]
  • Optical and Infrared Observations of SN 2002Dj: Some Possible Common Properties of Fast-Expanding Type Ia Supernovae
    Optical and infrared observations of SN 2002dj: some possible common properties of fast-expanding Type Ia supernovae G. Pignata,1,2 S. Benetti,3 P. A. Mazzali,4,5 R. Kotak,6 F. Patat,7 P. Meikle,8 M. Stehle,4 B. Leibundgut,7 N. B. Suntzeff,9 L. M. Buson,3 E. Cappellaro,3 A. Clocchiatti,2 M. Hamuy,1 J. Maza,1 J. Mendez,10 P. Ruiz-Lapuente,10 M. Salvo,11 B. P. Schmidt,11 M. Turatto3 and W. Hillebrandt4 1Departamento de Astronom´ıa, Universidad de Chile, Casilla 36-D, Santiago, Chile 2Departamento de Astronom´ıa y Astrof´ısica, Pontificia Universidad Catolica´ de Chile, Casilla 306, Santiago 22, Chile 3INAF Osservatorio Astronomico di Padova, Vicolo dell Osservatorio 5, I-35122 Padova, Italy 4Max-Planck-Institut fur¨ Astrophysik, Karl-Schwarzschild-Str. 1, D-85741 Garching bei Munchen,¨ Germany 5Osservatorio Astronomico di Trieste, Via Tiepolo 11, I-34131 Trieste, Italy 6Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, Belfast BT7 1NN 7European Southern Observatory, Karl-Schwarzschild-Str. 2, D-85748 Garching bei Munchen,¨ Germany 8Blackett Laboratory, Imperial College London, Prince Consort Road, London SW7 2BW 9Department of Physics, Texas A&M University, College Station, TX 77843-4242, USA 10Department of Astronomy, University of Barcelona, Marti i Franques 1, E-08028 Barcelona, Spain 11Research School of Astronomy and Astrophysics, Australian National University, Cotter Road, Weston Creek, ACT 2611, Australia ABSTRACT As part of the European Supernova Collaboration, we obtained extensive photometry and spectroscopy of the Type Ia supernova (SN Ia) SN 2002dj covering epochs from 11 d before to nearly two years after maximum.
    [Show full text]
  • Astro-Ph/0107318V1 17 Jul 2001 1562
    The Unique Type Ia Supernova 2000cx in NGC 524 Weidong Li1, Alexei V. Filippenko1, Elinor Gates2, Ryan Chornock1, Avishay Gal-Yam3,4, Eran O. Ofek3, Douglas C. Leonard5, Maryam Modjaz1, R. Michael Rich6, Adam G. Riess7, and Richard R. Treffers1 Email: [email protected], [email protected], [email protected] Received ; accepted arXiv:astro-ph/0107318v1 17 Jul 2001 1Department of Astronomy, University of California, Berkeley, CA 94720-3411. 2Lick Observatory, PO Box 82, Mount Hamilton, CA 95140. 3School of Physics and Astronomy, and the Wise Observatory, Tel Aviv University, Israel. 4Colton Fellow. 5Five College Astronomy Department, University of Massachusetts, Amherst, MA 01003- 9305. 6Department of Physics and Astronomy, University of California, Los Angeles, CA 90095- 1562. 7Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218. –2– ABSTRACT We present extensive photometric and spectroscopic observations of the Type Ia supernova (SN Ia) 2000cx in the S0 galaxy NGC 524, which reveal it to be peculiar. Photometrically, SN 2000cx is different from all known SNe Ia, and its light curves cannot be fit well by the fitting techniques currently available. There is an apparent asymmetry in the B-band peak, in which the premaximum brightening is relatively fast (similar to that of the normal SN 1994D), but the postmaximum decline is relatively slow (similar to that of the overluminous SN 1991T). The color evolution of SN 2000cx is also peculiar: the (B − V )0 color has a unique plateau phase and the (V − R)0 and (V − I)0 colors are very blue. Although the premaximum spectra of SN 2000cx are similar to those of SN 1991T-like objects (with weak Si II lines), its overall spectral evolution is quite different.
    [Show full text]
  • The Crab Nebula Imaged by the Hubble Space Telescope in 1999 and 2000
    Astronomers’ Observing Guides Other titles in this series The Moon and How to Observe It Peter Grego Double & Multiple Stars, and How to Observe Them James Mullaney Saturn and How to Observe it Julius Benton Jupiter and How to Observe it John McAnally Star Clusters and How to Observe Them Mark Allison Nebulae and How to Observe Them Steven Coe Galaxies and How to Observe Them Wolfgang Steinicke and Richard Jakiel Related titles Field Guide to the Deep Sky Objects Mike Inglis Deep Sky Observing Steven R. Coe The Deep-Sky Observer’s Year Grant Privett and Paul Parsons The Practical Astronomer’s Deep-Sky Companion Jess K. Gilmour Observing the Caldwell Objects David Ratledge Choosing and Using a Schmidt-Cassegrain Telescope Rod Mollise Martin Mobberley Supernovae and How to Observe Them with 167 Illustrations Martin Mobberley [email protected] Library of Congress Control Number: 2006928727 ISBN-10: 0-387-35257-0 e-ISBN-10: 0-387-46269-4 ISBN-13: 978-0387-35257-2 e-ISBN-13: 978-0387-46269-1 Printed on acid-free paper. © 2007 Springer Science+Business Media, LLC All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights.
    [Show full text]
  • Observations of Hydroxyl in Early-Type Galaxies
    Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 8 October 2018 (MN LATEX style file v2.2) Observations of hydroxyl in early-type galaxies James McBride1?, Katherine Alatalo2, and Kristina Nyland3;4 1Department of Astronomy, Campbell Hall, University of California, Berkeley, California 94720, USA 2Infrared Processing and Analysis Center, California Institute of Technology, Pasadena, California 91125, USA 3Netherlands Institute for Radio Astronomy (ASTRON), Postbus 2, 7990 AA Dwingeloo, The Netherlands 4Physics Department, New Mexico Tech, Socorro, NM 87801, USA 8 October 2018 ABSTRACT We used Arecibo Observatory and the Green Bank Telescope to observe OH in twelve early- type galaxies with known reservoirs of dense gas. We present three new detections of OH in absorption in the 1667 MHz line. One objective of our survey was to find evidence of molecular outflows, but our sensitivity, and the strength of the OH absorption, were insufficient to detect outflows. The detected sources have infrared luminosities and dust temperatures among the lowest of any galaxy detected in OH absorption. The ratio LHCN=LCO, a measure of the dense gas fraction in galaxies, is a powerful selector of OH megamasers for galaxies with high infrared luminosity. In early-type galaxies, which have much lower infrared luminosities, LHCN=LCO is also a promising tool for discovering OH, but in absorption rather than in maser emission. In addition to dense molecular gas, a radio continuum source and a favorable line-of-sight to the observer are likely key factors in detecting OH absorbers. Key words: galaxies: ISM — galaxies: elliptical and lenticular, cD — galaxies: evolution 1 INTRODUCTION served.
    [Show full text]
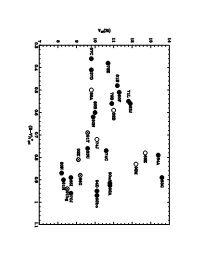
  • Statistical Connections Between the Properties of Type Ia Supernovae (Sne Ia) and the B–V Colors of Their Parent Galaxies Are Established
    TABLE 1 Type Ia SN SN Host Galaxy SNspectral V10(Si) ∆m15 −MB −MV o Galaxy (B−V )T type 1000 1937D N 1003 0.41 nor 9.8 ········· 1960F N4496A 0.51 nor 11.3 ········· 1961H N 4564 0.90 nor 8.3 ········· 1963J N3913 0.56 nor 11.9 ········· 1965I N 4753 0.89 nor 8.7 ········· 1967C N 3389 0.36 nor 9.8 ········· 1968E N2713 0.78 ··· 12.7 ········· 1970J N 7619 0.96 nor 8.7 ········· 1971L N6384 0.55 nor 11.8 ········· 1972E N 5253 0.38 nor 10.7 0.94 18.63 18.58 1974G N4414 0.77 nor 10.6 ········· 1974J N7343 0.72 ··· 10.1 ········· 1979B N3913 0.56 nor 10.9 ········· 1980N N 1316 0.87 nor 8.2 1.28 18.52 18.62 1981B N 4536 0.48 nor 11.2 1.1 18.87 18.83 1981D N1316 0.87 ········· 18.42 18.62 1982B N2268 0.59 ··· 11. ········· 1983G N4753 0.89 nor 13.6 ··· 18.33 18.52 1983U N 3227 0.76 nor 9.6 ········· 1984A N4419 0.79 nor 13.4 ··· 17.83∗ 18.12∗ 1986A N3367 0.50 ··· 9.8 ········· 1986G N 5128 0.88 86G 9.2 1.73 17.98 18.43 1989B N 3627 0.60 nor 10. 1.31 18.62 18.55 1989M N4579 0.74 nor ······ 18.54∗ 18.81∗ 1990M N5493 0.83 ··· 12.2 ········· 1990N N 4639 0.62 nor 9.9 1.01 18.75 18.84 1990T Anon 0.68 ······ 1.21 18.34 18.46 1990Y Anon 0.54 ······ 0.94 17.77∗ 18.16∗ 1990af Anon 0.92 nor 10.8 1.56 18.34 18.39 1991M I1151 0.39 ············ 17.83∗ arXiv:astro-ph/9510071v2 20 Nov 1995 1991S U5691 0.72 ······ 1.11 18.49 18.61 1991T N 4527 0.69 91T 9.6 0.94 19.53 19.50 1991U I4232 0.55 ······ 1.03 18.94 18.93 1991ag I4919 0.41 ······ 0.94 18.68 18.78 1991bg N 4374 0.94 91bg 8.5 1.88 16.31 17.18 1992A N 1380 0.92 nor 10.8 1.33 18.00 18.00 1992J Anon 0.94 ······ 1.35 ··· 18.47 1992K E269-.
    [Show full text]
  • The Peculiar Motions of Early-Type Galaxies in Two Distant Regions VII
    Mon. Not. R. Astron. Soc. 321, 277±305 (2001) The peculiar motions of early-type galaxies in two distant regions ± VII. Peculiar velocities and bulk motions Matthew Colless,1w R. P. Saglia,2 David Burstein,3 Roger L. Davies,4 Robert K. McMahan, Jr5 and Gary Wegner6 1Research School of Astronomy & Astrophysics, The Australian National University, Weston Creek, Canberra, ACT 2611, Australia 2Institut fuÈr Astronomie und Astrophysik, Scheinerstraûe 1, D-81679 Munich, Germany 3Department of Physics and Astronomy, Arizona State University, Tempe, AZ 85287-1504, USA 4Department of Physics, University of Durham, South Road, Durham DH1 3LE 5Department of Physics and Astronomy, University of North Carolina, CB#3255 Phillips Hall, Chapel Hill, NC 27599-3255, USA 6Department of Physics and Astronomy, Dartmouth College, Wilder Lab, Hanover, NH 03755, USA Accepted 2000 August 31. Received 2000 August 31; in original form 2000 May 23 ABSTRACT We present peculiar velocities for 85 clusters of galaxies in two large volumes at distances between 6000 and 15 000 km s21 in the directions of Hercules±Corona Borealis and Perseus±Pisces±Cetus (the EFAR sample). These velocities are based on Fundamental Plane (FP) distance estimates for early-type galaxies in each cluster. We fit the FP using a maximum likelihood algorithm which accounts for both selection effects and measurement errors, and yields FP parameters with smaller bias and variance than other fitting procedures. We obtain a best-fitting FP with coefficients consistent with the best existing determinations. We measure the bulk motions of the sample volumes using the 50 clusters with the best- determined peculiar velocities.
    [Show full text]
  • Astroparticle Physics at LHC
    MSc Physics Master Thesis Astroparticle physics at LHC Dark matter search in ATLAS by Michaël Muusse 6171885 September 2015 60 EC September 2013 – September 2015 Supervisor/Examiner: Examiner: Dr. D. Berge Dr. M. Vreeswijk ... Astroparticle physics at the LHC Dark matter search in ATLAS Astrophysics at the LHC – Dark matter seach in ATLAS ii Astrophysics at the LHC – Dark matter seach in ATLAS iii Astroparticle physics at the LHC Dark matter search in ATLAS Master thesis in Physics Michael Muusse July 2015 Track: Grappa, University of Amsterdam Supervisor: Dr. D. Berge 2nd supervisor: Dr. D. Salek Second Reviewer: Dr. M. Vreeswijk ... Astrophysics at the LHC – Dark matter seach in ATLAS iv Front cover image credit: [14] [178] edited. Astrophysics at the LHC – Dark matter seach in ATLAS v Abstract Astroparticle physics at the LHC – Dark matter search in ATLAS In astronomy and cosmology the hypothesized existence of dark matter and its properties are inferred indirectly from observed gravitational effects. An explanation for the missing mass problem in the study of motion of galaxies and clusters, the shape of galactic rotation curves, observations on weak gravitational lens effects near clusters and the correspondence between the cosmic microwave background anisotropies and the large- scale structure of the Universe, could be given by a form of non electromagnetic interacting, invisible matter, hence called dark matter. An undetected heavy elementary relic particle that interacts only trough the gravitational and weak forces is a leading candidate for dark matter. Furthermore elementary particles with Weakly Interacting Massive Particle (WIMP) properties arise often in theories beyond the standard model.
    [Show full text]