Predictability of Weather and Climate, T.Palmer and R
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Download This List As PDF Here
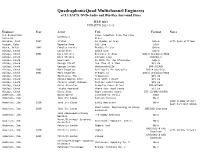
QuadraphonicQuad Multichannel Engineers of 5.1 SACD, DVD-Audio and Blu-Ray Surround Discs JULY 2021 UPDATED 2021-7-16 Engineer Year Artist Title Format Notes 5.1 Production Live… Greetins From The Flow Dishwalla Services, State Abraham, Josh 2003 Staind 14 Shades of Grey DVD-A with Ryan Williams Acquah, Ebby Depeche Mode 101 Live SACD Ahern, Brian 2003 Emmylou Harris Producer’s Cut DVD-A Ainlay, Chuck David Alan David Alan DVD-A Ainlay, Chuck 2005 Dire Straits Brothers In Arms DVD-A DualDisc/SACD Ainlay, Chuck Dire Straits Alchemy Live DVD/BD-V Ainlay, Chuck Everclear So Much for the Afterglow DVD-A Ainlay, Chuck George Strait One Step at a Time DTS CD Ainlay, Chuck George Strait Honkytonkville DVD-A/SACD Ainlay, Chuck 2005 Mark Knopfler Sailing To Philadelphia DVD-A DualDisc Ainlay, Chuck 2005 Mark Knopfler Shangri La DVD-A DualDisc/SACD Ainlay, Chuck Mavericks, The Trampoline DTS CD Ainlay, Chuck Olivia Newton John Back With a Heart DTS CD Ainlay, Chuck Pacific Coast Highway Pacific Coast Highway DTS CD Ainlay, Chuck Peter Frampton Frampton Comes Alive! DVD-A/SACD Ainlay, Chuck Trisha Yearwood Where Your Road Leads DTS CD Ainlay, Chuck Vince Gill High Lonesome Sound DTS CD/DVD-A/SACD Anderson, Jim Donna Byrne Licensed to Thrill SACD Anderson, Jim Jane Ira Bloom Sixteen Sunsets BD-A 2018 Grammy Winner: Anderson, Jim 2018 Jane Ira Bloom Early Americans BD-A Best Surround Album Wild Lines: Improvising on Emily Anderson, Jim 2020 Jane Ira Bloom DSD/DXD Download Dickinson Jazz Ambassadors/Sammy Anderson, Jim The Sammy Sessions BD-A Nestico Masur/Stavanger Symphony Anderson, Jim Kverndokk: Symphonic Dances BD-A Orchestra Anderson, Jim Patricia Barber Modern Cool BD-A SACD/DSD & DXD Anderson, Jim 2020 Patricia Barber Higher with Ulrike Schwarz Download SACD/DSD & DXD Anderson, Jim 2021 Patricia Barber Clique Download Svilvay/Stavanger Symphony Anderson, Jim Mortensen: Symphony Op. -

&Blues GUITAR SHORTY
september/october 2006 issue 286 free jazz now in our 32nd year &blues report www.jazz-blues.com GUITAR SHORTY INTERVIEWED PLAYING HOUSE OF BLUES ARMED WITH NEW ALLIGATOR CD INSIDE: 2006 Gift Guide: Pt.1 GUITAR SHORTY INTERVIEWED Published by Martin Wahl By Dave Sunde Communications geles on a rare off day from the road. Editor & Founder Bill Wahl “I would come home from school and sneak in to my uncle Willie’s bedroom Layout & Design Bill Wahl and try my best to imitate him playing the guitar. I couldn’t hardly get my Operations Jim Martin arms over the guitar, so I would fall Pilar Martin down on the floor and throw tantrums Contributors because I couldn’t do what I wanted. Michael Braxton, Mark Cole, Grandma finally had enough of all that Dewey Forward, Steve Homick, and one morning she told my Uncle Chris Hovan, Nancy Ann Lee, Willie point blank, I want you to teach Peanuts, Mark Smith, Dave this boy how to ‘really’ play the guitar Sunde, Duane Verh and Ron before I kill him,” said Shorty Weinstock. Photos of Guitar Shorty Fast forward through years of late courtesy of Alligator Records night static filled AM broadcasts crackling the southbound airwaves out of Cincinnati that helped further de- Check out our costantly updated website. Now you can search for CD velop David’s appreciative musical ear. Reviews by artists, Titles, Record T. Bone Walker, B.B. King and Gospel Labels, keyword or JBR Writers. 15 innovator Sister Rosetta Tharpe were years of reviews are up and we’ll be the late night companions who spent going all the way back to 1974. -

Al Di Meola New World Sinfonia
This pdf was last updated: Jan/10/2011. Al Di Meola New World Sinfonia Al Di Meola is one of the most prominent virtuosos in contemporary jazz. The upcoming tour will follow the release of the new studio album "Pursuit of Radical Rhapsody" on March 15, 2011 (Universal) which features guests like Charlie Haden, Gonzalo Rubalcaba, Peter Erskine and Barry Miles. A true highlight! Line-up Al Di Meola - guitar Kevin Seddiki - guitar Fausto Beccalossi - accordion Peter Kaszas - drums Plus: Csaba Tot Bagi - technician Laura Wilson - roadmanagement On Stage: 4 Travel Party: 6 Website www.aldimeola.com Biography Al Di Meola's highly celebrated career has spanned a wide range of emotions into a unique style embodying the artists world inspired influences. From the beginning of his solo career, where records like 'Land of the Midnight Sun', 'Elegant Gypsy' and 'Casino' were amongst the highest selling records of any instrumental artist at that time, Al Di Meola continues to make, with respect, startling achievements in music pioneering while the decline of U.S. radio continues to elude most interesting contemporary music.Al Di Meola, again and again, reveals himself as a seasoned gifted contemporary composer and a player of deepening grace and evocative lyricism. He has been continually sited by many of the top prominent Music critics around the world for his virtuosic guitar work and compositions. Al's intrigue with complex rhythmic syncopation combined with provocative lyrical melodies always incorporating, sophisticated harmony at the root of these serious but heart felt works is central and foremost. Influenced greatly by jazz guitarist Larry Coryell, Di Meola had enrolled at Berklee College of Music in Boston, here his marathon practice sessions are still the stuff of legends. -

Frickler Unter Sich
# 2006/49 dschungel https://jungle.world/artikel/2006/49/frickler-unter-sich Frickler unter sich Von Jan Süselbeck Was ist eigentlich aus den guten, alten Helden an der Fusion-Gitarre geworden? Aktuelle Jazz-CDs üblicher Verdächtiger. von jan süselbeck Unter dem Einfluss von Jimi Hendrix’ »Electric Ladyland« (1968), Miles Davis’ »Bitches Brew« (1969) und den ersten Platten von John McLaughlins Mahavishnu Orchestra zu Beginn der Siebziger war der E-Gitarre im Jazz eine neue Bedeutung zugewachsen. Was jedoch folgte, ist oft genug beklagt worden: Alben wie Al Di Meolas »Land Of The Midnight Sun« (1976) präsentierten muckibudenartige Fingerakrobatik, deren Verblüffungseffekt schnellstens verpuffte und den Eindruck intellektueller Schlichtheit hinterließ. Uli Krug hat in seiner Prog-Rock-Artikelserie in der Jungle World allerdings daran erinnert, dass längst nicht alles Mumpitz war, was seit den späten Sechzigern im Grenzgebiet von Jazz, Klassik, Blues, Folk und Rock entstand, bevor Ende der siebziger Jahre der Punk aufkam und das progressive Genre im Mainstream versandete. Mittlerweile behaupten Bands wie The Mars Volta sogar, ihr aufgefrischter Prog-Rock sei der wahre Punk unserer Tage. Kündigt sich damit etwa auch eine Renaissance des virtuosen Jazzrock-Genres alter Schule an? John McLaughlin beispielsweise produziert nach wie vor fleißig Platten und geriert sich darauf als eine Art Gastgeber nachgewachsener Talente. Auf seiner letzten mit dem albernen Titel »Industrial Zen« (2005) gibt es ein Gastsolo des US-Gitarristen Eric Johnson. Sicher nicht von ungefähr: Ist Johnson doch einer der auch schon nicht mehr ganz so jungen Musiker, in deren Spiel die Anleihen bei Hendrix mit am deutlichsten herauszuhören sind. Johnson bezieht sich damit auf die »gute alte Zeit«, in der auch McLaughlins innovativste Arbeiten entstanden sind. -

Publicacion7135.Pdf
BIBLIOTECA PÚBLICA DE ALICANTE BIOGRAFÍA Roy Haynes nació el 13 de marzo de 1925 en Boston, Massachusetts. A finales de los años cuarenta y principios de los cincuenta, Roy Haynes tuvo la clase de aprendizaje que constituiría el sueño de cualquier músico actual: sentarse en el puesto de baterista y acompañar al gran Charlie Parker. Ahora, cincuenta años después, y tras haber tocado con todos los grandes del jazz: Thelonius Monk, Miles Davis, o Bud Powell, todavía coloca sus grabaciones en la cima de las listas de las revistas especializadas en jazz. Este veterano baterista, comenzó su andadura profesional en las bigbands de Frankie Newton y Louis Russell (1945-1947) y el siguiente paso fue tocar entre 1947 y 1949 con el maestro el saxo tenor, Lester Young. Entre 1949 y 1952, formo parte del quinteto de Charlie Parker y desde ese privilegiado taburete vio pasar a las grandes figuras del bebop y aprender de ellas. Acompañó a la cantante Sarah Vaughan, por los circuitos del jazz en los Estados Unidos entre 1953 y 1958 y cuando finalizó su trabajo grabo con Thelonious Monk, George Shearing y Lennie Tristano entre otros y ocasionalmente sustituía a Elvin Jones en el cuarteto de John Coltrane. Participó en la dirección de la Banda Sonora Original de la película "Bird" dirigida por Clint Eastwood en 1988 y todavía hoy en activo, Roy Haynes, es una autentica bomba dentro de un escenario como pudimos personalmente comprobar en uno de sus últimos conciertos celebrados en España y mas concretamente en Sevilla en el año 2000. En 1994, Roy Haynes recibió el premio Danish Jazzpar, que se concede en Dinamarca. -

Top 5 Chieftains Albums
JazzWeek with airplay data powered by jazzweek.com • January 8, 2007 Volume 3, Number 7 • $7.95 World Music Q&A: The Chieftains’ PADDY MOLONEY On The Charts: #1 Jazz Album – Diana Krall #1 Smooth Album – Benson/Jarreau #1 College Jazz – Madeleine Peyroux #1 Smooth Single – George Benson #1 World Music – Lynch/Palmieri JazzWeek This Week EDITOR/PUBLISHER Ed Trefzger anuary 10-13 marks the 2007 International Association MUSIC EDITOR Tad Hendrickson fo Jazz Education Annual Conference. Here’s a quick Jplug for the events JazzWeek is sponsoring each day CONTRIBUTING WRITER/ from 10:00 a.m. to noon: PHOTOGRAPHER Tom Mallison Thursday Workshop: Jazz Radio In Crisis: Why That’s A Good Thing PHOTOGRAPHY Barry Solof This session will focus on why some stations are disappearing or seeing big drops in audience, whie other stations with more progressiveapproaches are Contributing Editors seeing audience increases. Panelists will discuss the adoption of more youth- Keith Zimmerman oriented music, the realization that there’s a younger demographic during lat- Kent Zimmerman er hours, and the success stations programming for that audience are seeing. Founding Publisher: Tony Gasparre Panelists: Bob Rogers, Bouille & Rogers consultants; Jenny Toomey, Future of Music Coalition; Gary Vercelli, KXJZ; Linda Yohn, WEMU; Rafi Za- ADVERTISING: Devon Murphy bor. Location: Riverside Ballroom, Sheraon 3rd Fl. Call (866) 453-6401 ext. 3 or email: [email protected] Friday Workshop: Jazz Radio and the Community: How to Make Your Station More Relevant. Stations around the country have made their pro- SUBSCRIPTIONS: gramming more in tune with the local community by reaching out to arts Free to qualified applicants Premium subscription: $149.00 per year, organizations, schools, colleges and universities. -

2010 Music Accessories Equipment
Product Catalog / Winter 2009 - 2010 Music Accessories Equipment ELUSIVE DISC To order Toll Free call: Fax: 765-608-5341 4020 Frontage Rd. Anderson, IN 46013 Info: 765-608-5340 SHOP ON-LINE AT: 1-800-782-3472 e-mail: [email protected] www.elusivedisc.com ContentsSACD SACD SACD 1-35 Accessories 74-80 04. Analogue Productions 75. Gingko Audio 10. Chesky 78. Mobile Fidelitiy 15. Fidelio Audio 78. Record Research Labs 15. Groove Note 79. Audioquest 21. Mercury Living Presence 80. Audience 21. Mobile Fidelity 80. VPI 24. Pentatone 80. Michael Fremer 25. Polydor 80. Shakti 27. RCA 28. Sony 31. Stockfisch Equipment 81-96 31. Telarc 35. Virgin 81. Amps / Tuners / Players 83. Cartridges 86. Headphones XRCD 36-39 89. Loudspeakers 90. Phono Stages 36. FIM 92. Record Cleaners 36. JVC 93. Tonearms 94. Turntables Vinyl 40-73 41. Analogue Productions 43. Cisco 43. Classic Records 48. EMI 52. Get Back 53. Groove Note Records 54. King Super Analogue 55. Mobile Fidelity 57. Pure Pleasure Records 59. Scorpio 59. Simply Vinyl 60. Sony 60. Speaker’s Corner 63. Stockfisch 63. Sundazed 66. Universal 68. Vinyl Lovers 69. Virgin 69. WEA 4020 Frontage Rd. Info: 765-608-5340 72. Warner Brothers / Rhino Anderson, IN 46013 Orders: 800-782-3472 www.elusivedisc.com SACD SACD The Band / Music From Big Pink Pink Floyd / The Dark Side Of The Moon Tracked in a time of envelope-pushing Arguably the greatest rock album ever studio experimentations and pop released now available for the first psychedelia, Music From Big Pink is a time in Super Audio CD! This marks watershed album in the history of rock. -

Al Di Meola MP3 Collection Mp3, Flac, Wma
Al Di Meola MP3 Collection mp3, flac, wma DOWNLOAD LINKS (Clickable) Genre: Jazz / Rock / Latin Album: MP3 Collection Country: Russia Style: Contemporary Jazz, Fusion, Tango MP3 version RAR size: 1626 mb FLAC version RAR size: 1253 mb WMA version RAR size: 1901 mb Rating: 4.8 Votes: 986 Other Formats: MP4 WAV AC3 MMF RA AU AC3 Tracklist Land Of The Midnight Sun 1 The Wizard 2 Land Of The Midnight Sun 3 Sarabande From Violin Sonata In B Minor 4 Love Theme From "Pictures Of The Sea" 5 Suite Golden Dawn 6 Short Tales Of The Black Forest Elegant Gypsy 7 Flight Over Rio 8 Midnight Tango 9 Mediterranean Sundance 10 Race With Devil On Spanish Highway 11 Lady Of Rome, Sister Of Brazil 12 Elegant Gypsy Suite Splendido Hotel 13 Alien Chase On Arabian Desert 14 Silent Story In Her Eyes 15 Roller Jubilee 16 Two To Tango 17 Al Di's Dream Theme 18 Dinner Music Of The Gods 19 Splendido Sundance 20 I Can Tell 21 Spanish Eyes 22 Isfahan 23 Bianca's Midnight Lullaby Electric Rendevous 24 God Bird Change 25 Electric Rendevous 26 Passion, Grace & Fire 27 Cruisin' 28 Black Cat Shuffle 29 Ritmo De La Noche 30 Somalia 31 Jewel Inside The Dream Friday Night In San Francisco 32 Mediterranean Sundance 33 Short Tales Of The Black Forest 34 Frevo Rasgado 35 Fantasia Suite 36 Guardian Angel Tirami Su 37 Beijing Demons 38 Arabella 39 Smile From A Stranger 40 Rhapsody Of Fire 41 Song To The Pharaoh Kings 42 Andonea 43 Maraba 44 Song With A View 45 Tirami Su (Part I) 46 July 47 Soaring Through A Dream Al Di Meola, Larry Coryell, Bireli Lagrene - Super Guitar Trio 48 P.S.P. -

Al Di Meola - Speak a Volcano
Al Di Meola - Speak A Volcano http://www.concertdvdreviews.com/Reviews/DiMeola_Electric.htm Al Di Meola - Speak A Volcano (Return to Electric Guitar) Performance Production When I first saw the advertisement for this DVD showing Al Di Meola playing the electric guitar, I just couldn't wait to get my hands on the thing. As much as I love Di Meola's acoustic guitar playing - he is certainly one of the world's best - it was the blazing electric jazz fusion of his early solo albums, as well as his work with Chick Corea's Return To Forever, that really made me a fan. Up until now, Di Meola's only live music videos have been solely acoustic based. His two Live At Montreux releases, 1986/1993, and 1994, with Jean-Luc Ponty and Stanley Clarke, both brilliantly showcased some amazing acoustic guitar performances, but what about his legendary electric guitar output? Speak A Volcano is certainly a fitting title for a live Al Di Meola performance, because his playing can be that explosive, but the subtitle, A Return To Electric Guitar, is a tad misleading. Speak A Volcano was recorded at Leverkusener Jazztage, Germany, in November 2006 and captures one of the world's greatest jazz fusion guitarists sounding stronger than ever 30 years after the release of his debut solo album Land Of The Midnight Sun in 1976. The guy looks like he hasn't aged in thirty years either. Dressed in black jeans, a long sleeve black tee shirt, and a head full of thick black hair, the 60 year old Di Meola looks fit enough to be playing left-wing for the Boston Bruins. -

Quadraphonicquad Multichannel Engineers of All Surround Releases
QuadraphonicQuad Multichannel Engineers of all surround releases JULY 2021 UPDATED 2021-7-16 Type Engineer Year Artist Title Format Notes 5.1 Production Live… Greetins From The Flow MCH Dishwalla Services, State MCH Abraham, Josh 2003 Staind 14 Shades of Grey DVD-A with Ryan Williams Quad Abramson, Mark 1973 Judy Collins Colors of the Day - The Best Of CD-4/Q8/QR/SACD MCH Acquah, Ebby Depeche Mode 101 Live SACD The Outrageous Dr. Stolen Goods: Gems Lifted from P: Alan Blaikley, Ken Quad Adelman, Jack 1972 Teleny's Incredible CD-4/Q8/QR/SACD the Masters Howard Plugged-In Orchestra MCH Ahern, Brian 2003 Emmylou Harris Producer’s Cut DVD-A MCH Ainlay, Chuck David Alan David Alan DVD-A MCH Ainlay, Chuck 2005 Dire Straits Brothers In Arms DVD-A DualDisc/SACD MCH Ainlay, Chuck Dire Straits Alchemy Live DVD/BD-V MCH Ainlay, Chuck Everclear So Much for the Afterglow DVD-A MCH Ainlay, Chuck George Strait One Step at a Time DTS CD MCH Ainlay, Chuck George Strait Honkytonkville DVD-A/SACD MCH Ainlay, Chuck 2005 Mark Knopfler Sailing To Philadelphia DVD-A DualDisc MCH Ainlay, Chuck 2005 Mark Knopfler Shangri La DVD-A DualDisc/SACD MCH Ainlay, Chuck Mavericks, The Trampoline DTS CD MCH Ainlay, Chuck Olivia Newton John Back With a Heart DTS CD MCH Ainlay, Chuck Pacific Coast Highway Pacific Coast Highway DTS CD MCH Ainlay, Chuck Peter Frampton Frampton Comes Alive! DVD-A/SACD MCH Ainlay, Chuck Trisha Yearwood Where Your Road Leads DTS CD MCH Ainlay, Chuck Vince Gill High Lonesome Sound DTS CD/DVD-A/SACD QSS: Ron & Howard Quad Albert, Ron & Howard 1975 -
Five Essential Billy Strayhorn Songs
JazzWeek with airplay data powered by jazzweek.com • January 29, 2007 Volume 3, Number 10 • $7.95 Artist Q&A: CHARLES TOLLIVER page 9 On The Charts: #1 Jazz Album – Jimmy Heath Big Band #1 World Music – Lynch/Palmieri #1 College Jazz – Medeski Scofield Martin & #1 Smooth Album – For Luther II Wood #1 Smooth Single – Kirk Whalum JazzWeek This Week EDITOR/PUBLISHER Ed Trefzger he performance of the Charles Tolliver Big Band on the MUSIC EDITOR Tad Hendrickson closing night of IAJE 2007 was nothing short of stun- Tning. Tad Hendrickson caught up with Tolliver a few CONTRIBUTING WRITER/ days after IAJE, and finds out just where he’s been all these PHOTOGRAPHER Tom Mallison years. PHOTOGRAPHY Barry Solof Registration for the 2007 JazzWeek Summit, its sixth (!) Contributing Editors annual incarnation, will open on Feb. 1. Current paid sub- Keith Zimmerman scribers will get an email notice about discounted registration. Kent Zimmerman The Summit will be held at the same locationas last year – the Founding Publisher: Tony Gasparre Rochester Clarion Riverside – side-by-side with the Roches- ADVERTISING: Devon Murphy ter International Jazz Festival. Dates are June 7-9, 2007. Call (866) 453-6401 ext. 3 or There will be performance and sponsorship opportunities email: [email protected] at the Summit; details will follow shortly. SUBSCRIPTIONS: We’re looking for input on panel sessions, too. While there Free to qualified applicants Premium subscription: $149.00 per year, are some basics we wish to cover each year, we also are look- w/ Industry Access: $249.00 per year ing for some “master classes,” too. -

Jazz Radio Panel P. 21 Jazzweek.Com • January 22, 2007 Jazzweek 12 Airplay Data Jazzweek Jazz Album Chart Jan
JazzWeek with airplay data powered by jazzweek.com • January 22, 2007 Volume 3, Number 9 • $7.95 Industry Q&A: IAJE’s BILL McFARLIN page 9 Remembering ... MICHAEL BRECKER and ALICE COLTRANE page 4 On The Charts: #1 Jazz Album – MB3 #1 Smooth Album – For Luther II #1 College Jazz – Madeleine Peyroux #1 Smooth Single – George Benson #1 World Music – Lynch/Palmieri JazzWeek This Week EDITOR/PUBLISHER Ed Trefzger he passing of Michael Brecker and Alice Coltrane last MUSIC EDITOR Tad Hendrickson week was certainly a sad moment for all of us in the jazz Tcommunity. But how touching and special it was for that CONTRIBUTING WRITER/ community to be together to mourn that passing. PHOTOGRAPHER Tom Mallison There was hardly a dry eye in the house on the last night PHOTOGRAPHY of IAJE as Charlie Haden took the stage with the Liberation Barry Solof Music Orchestra and spoke a few words. Having performed Contributing Editors with both and having been close with Michael since Brecker’s Keith Zimmerman days as a student, Haden was deeply saddened and overcome. Kent Zimmerman The music of the LMO and of Haden is always very moving Founding Publisher: Tony Gasparre to me, and with the selection of tunes and the solemnity of ADVERTISING: Devon Murphy the moment, it was a touching and fitting tribute – a wake for Call (866) 453-6401 ext. 3 or the departed, and a very spiritual moment. email: [email protected] SUBSCRIPTIONS: On a personal note, I have watched Michael’s situation Free to qualified applicants Premium subscription: $149.00 per year, with keen interest.