DOCSLIB.ORG

Lecture 2 Chemical Kinetics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 2 Chemical Kinetics 6/26/11 Lecture 2 Chemical Kinetics 1 Chemical Kinetics One (elementary) step reaction N N ν ν iMi → i Mi i=1 i=1 N is the number of species νi, νi are the stoichiometric coefficients νi =0ifi is not a reactant νi =0ifi is not a product Example: H +O 2OH 2 2 → N =3 H2 (i = 1) : ν1 =1 ν1 =0 O2 (i = 2) : ν2 =1 ν2 =0 OH (i = 3) : ν3 =0 ν3 =2 2 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 1 6/26/11 N N ν ν iMi → i Mi i=1 i=1 there is a relation between the change in the number of moles of each species; i.e., for any two species i and j dn dn i = j ν ν ν ν i − i j − j Ifω ˆi is the time rate of change of the concentration of species i (moles, per unit volume per second), i.e.,ω ˆi = dCi/dt,then ωˆ ωˆ i = j ν ν ν ν i − i j − j ωˆ ωˆ or i = j = ω ν ν ν ν i − i j − j and we may the common ratio ω, which is species independent, as the reaction rate (moles per unit volume per second) 3 Law of Mass Action phenomenological law that was verified experimentally the reaction rate is proportional to the products of the concentrations reactants N νi ω = k(T ) Ci i=1 (specific) reaction rate constant the units of k depend on the reaction order n = νi (n 1) 1 and is [concentration − time]− · example CH +2O CO +2HO 4 2 → 2 2 ωˆ ωˆ ωˆ ωˆ H2O = CO2 = CH4O = O2 = ω 2 1 − 1 − 2 ω = kC C2 CH4 O2 4 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 2 6/26/11 Chemical reaction involving M elementary steps N N ν ν j =1, 2,...,M i,jMi → i,jMi i=1 i=1 where forward and backward reactions are written as separate steps M net rate of production of species i ωˆi = ωˆi,j j=1 M ωˆ = (ν ν ) ω i i,j − i,j j j=1 where ωj is the reaction rate of the elementary step j, namely N νi,j ωj = k(T ) Ci i=1 5 Chain reaction - hydrogen-bromine reaction k1 Br2 +M 2Br + M k→2 Br + H2 HBr + H →k3 H + Br HBr + Br H2 +Br2 2HBr 2 ⇒ → →k4 H + HBr Br + H2 →k 2Br + M 5 Br +M → 2 5 5 νi,j ωˆ = (ν ν ) ω ωj = k(T ) C i i,j − i,j j i j=1 i=1 i =H2,Br2, H, Br, HBr for example dC ωˆ = Br =2k C k C C + k C C + k C C 2k C2 Br dt 1 Br2 − 2 Br H2 3 H Br2 4 H HBr − 5 Br 6 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 3 6/26/11 Two of the important questions in chemical kinetics are determine all the elementary steps by which a given chemical reaction • actually proceeds determine the specific rate constant for each step • 7 Reaction Mechanisms First order decomposition reaction • One step opposing reactions • Chain reaction • Reduced mechanisms modeling • 8 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 4 6/26/11 First order decomposition reaction A k B → Ca dC CA(0) A = kC C (0) given dt A A k kt CA = CA(0)e− t 1 C (0) t = ln A 1 k C tc A ⇒ ∼ k characteristic time scale large k corresponds to a small time scale or very fast reaction this is a source of stiffness in the differential equations 9 One step opposing reaction k A f B →k B b A → dC A = k C + k C dt f A b B − C (0) specified, C (0) = 0 dC A B B = k C k C dt f A − b B d k k C C = M C M = − f b C = A dt · kf kb CB − λ1t λ2t C = V1e + V2e 1 1 there are two characteristic times, corresponding to λ1− and λ2− 10 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 5 6/26/11 k λ k λ1 =0, − f − b =0 k k λ λ = (k + k ) f − b − ⇒ 2 f b − CA CA(0) kb kf CA(0) 1 (k +k )t = + e− f b CB k + k kf k + k 1 f b f b − C 1 1 A = Ceq + Ceq e (kf +kb)t C A k /k B 1 − B f b − eq kb eq kf CA = CA(0) CB = CA(0) kf + kb kf + kb 1 the characteristic times are t1 = and t2 =(kf + kb)− corresponding to the ∞ 1 1 reciprocal of the eigenvalues; i.e., λ1− and λ2− at equilibrium, k Ceq k Ceq =0 f A − b B 11 In fact, for this simple system, one easily see that d [C + C ]=0 dt A B d [k C k C ]= (k + k )[k C k C ] dt f A − b B − f b f A − b B z1 = CA + CB d z 00 z 1 = 1 z2 = kf CA kbCB ⇒ dt z2 0 (kf +kb) z2 − − 0 z1 = z1(0) e (kf +kb)t z2 = z2(0) e− CA + CB = CA(0) (kf+kb)t kf CA kbCB = kf CA(0)e− CB − C B k b − C A f when kf + kb 1, the characteristic times are k 1 t1 = 0 (slow time) and t2 =(kf + kb)− (fast time) CA CA + CB is a conserved quantity, kf CA kbCB 0 almost all the time − ≈ 12 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 6 6/26/11 Chain Reaction Hydrogen-Bromine Reaction any halogen molecule (F2,CL2 or I2) may replace Br2 H +Br 2 HBr 2 2 → k Br +M 1 2Br + M chain initiating 2 → k Br + H 2 HBr + H 2 → k H + Br 3 HBr + Br chain carrying 2 → k H + HBr 4 Br + H → 2 k 2Br + M 5 Br +M chain terminating → 2 the intermediates H, Br are the chain carriers 13 k1 Br2 +M 2Br + M k→2 Br + H2 HBr + H →k3 H + Br HBr + Br H2 +Br2 2HBr 2 ⇒ → →k4 H + HBr Br + H2 →k 2Br + M 5 Br +M → 2 dC HBr = k C C + k C C k C C dt 2 Br H2 3 H Br2 − 4 H HBr dC H = k C C k C C k C C dt 2 Br H2 − 3 H Br2 − 4 H HBr dC Br =2k C k C C + k C C + k C C 2k C2 dt 1 Br2 − 2 Br H2 3 H Br2 4 H HBr − 5 Br dC H2 = k C C + k C C dt − 2 Br H2 4 H HBr dC Br2 = k C k C C + k C2 dt − 1 Br2 − 3 H Br2 5 Br 14 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 7 6/26/11 We are faced with a set of N nonlinear coupled differential equations (for spa- tially homogeneous system, as discussed here, these are ODEs), with N generally a large number The description of the combustion of real fuels may involve 1000 species or more, involved in a complex network of elementary steps that add up to few thousands. For example, the detailed kinetic mechanism of the primary reference fuel (PRF) contains 1034 species participating in 4236 elementary reactions1. 1 H.J. Curran, P. Gaffuri, W.J. Pitz and C.K. Westbrook (C&F 2002) 15 16 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 8 6/26/11 chemical physical Lme scales Lme scales slow Lme scales 100 s (NO formaon) 10-2 s Intermediate Lme scales of flow, Lme scales 10-4 s transport, turbulence 10-6 s fast Lme scales (steady-state, -8 parLal equilibrium) 10 s Illustraon of the various Lmes scales governing chemical reacLng flows 17 k1 Br2 +M 2Br + M k→ Br + H 2 HBr + H 2 → k3 H +Br 2HBr H + Br2 HBr + Br ⇒ 2 2 → →k4 H + HBr Br + H2 →k 2Br + M 5 Br +M → 2 Radicals form and react very rapidly (at nearly equal rates) such that their concentraons remains nearly constant dC dCH Br 0 0 dt ≈ dt ≈ Rate of formaon of HBr dC HBr = k C C + k C C k C C dt 2 Br H2 3 H Br2 − 4 H HBr 18 Copyright ©2011 by Moshe Matalon. This material is not to be sold, reproduced or distributed without the prior wri@en permission of the owner, M. Matalon. 9 6/26/11 dC H 0 k C C k C C k C C =0 dt ≈ ⇒ 2 Br H2 − 3 H Br2 − 4 H HBr dC Br 0 2k C k C C +k C C +k C C 2k C2 =0 dt ≈ ⇒ 1 Br2 − 2 Br H2 3 H Br2 4 H HBr − 5 Br 1/2 k1 1/2 k2 k1/k5 CH C C = C 2 Br2 Br Br2 CH = k5 k C + k C 3 Br2 4 HBr 2k k /k C C1/2 dCHBr 2 1 5 H2 Br2 = 1 ⇒ dt 1+(k /k )C C− 4 3 HBr Br2 dC HBr =2k C C dt 0 H2 Br2 19 2k k /k C C1/2 dCHBr 2 1 5 H2 Br2 = 1 dt 1+(k /k )C C− 4 3 HBr Br2 dCHBr 1/2 2k0 CH C when k4/k3 1; (k0 = k2 k1/k5) dt ≈ 2 Br2 N ni ω = k Ci i = reactants only i=1 20 Copyright ©2011 by Moshe Matalon.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • Free Radical Reactions (Read Chapter 4) A
    Chemistry 5.12 Spri ng 2003, Week 3 / Day 2 Handout #7: Lecture 11 Outline IX. Free Radical Reactions (Read Chapter 4) A. Chlorination of Methane (4-2) 1. Mechanism (4-3) B. Review of Thermodynamics (4-4,5) C. Review of Kinetics (4-8,9) D. Reaction-Energy Diagrams (4-10) 1. Thermodynamic Control 2. Kinetic Control 3. Hammond Postulate (4-14) 4. Multi-Step Reactions (4-11) 5. Chlorination of Methane (4-7) Suggested Problems: 4-35–37,40,43 IX. A. Radical Chlorination of Methane H heat (D) or H H C H Cl Cl H C Cl H Cl H light (hv) H H Cl Cl D or hv D or hv etc. H C Cl H C Cl H Cl Cl C Cl H Cl Cl Cl Cl Cl H H H • Why is light or heat necessary? • How fast does it go? • Does it give off or consume heat? • How fast are each of the successive reactions? • Can you control the product ratio? To answer these questions, we need to: 1. Understand the mechanism of the reaction (arrow-pushing!). 2. Use thermodynamics and kinetics to analyze the reaction. 1 1. Mechanism of Radical Chlorination of Methane (Free-Radical Chain Reaction) Free-radical chain reactions have three distinct mechanistic steps: • initiation step: generates reactive intermediate • propagation steps: reactive intermediates react with stable molecules to generate other reactive intermediates (allows chain to continue) • termination step: side-reactions that slow the reaction; usually combination of two reactive intermediates into one stable molecule Initiation Step: Cl2 absorbs energy and the bond is homolytically cleaved.
    [Show full text]
  • Glossary of Scientific Terms in the Mystery of Matter
    GLOSSARY OF SCIENTIFIC TERMS IN THE MYSTERY OF MATTER Term Definition Section acid A substance that has a pH of less than 7 and that can react with 1 metals and other substances. air The mixture of oxygen, nitrogen, and other gasses that is consistently 1 present around us. alchemist A person who practices a form of chemistry from the Middle Ages 1 that was concerned with transforming various metals into gold. Alchemy A type of science and philosophy from the Middle Ages that 1 attempted to perform unusual experiments, taking something ordinary and turning it into something extraordinary. alkali metals Any of a group of soft metallic elements that form alkali solutions 3 when they combine with water. They include lithium, sodium, potassium, rubidium, cesium, and francium. alkaline earth Any of a group of metallic elements that includes beryllium, 3 metals magnesium, calcium, strontium, barium, and radium. alpha particle A positively charged particle, indistinguishable from a helium atom 5, 6 nucleus and consisting of two protons and two neutrons. alpha decay A type of radioactive decay in which a nucleus emits 6 an alpha particle. aplastic anemia A disorder of the bone marrow that results in too few blood cells. 4 apothecary The person in a pharmacy who distributes medicine. 1 atom The smallest component of an element that shares the chemical 1, 2, 3, 4, 5, 6 properties of the element and contains a nucleus with neutrons, protons, and electrons. atomic bomb A bomb whose explosive force comes from a chain reaction based on 6 nuclear fission. atomic number The number of protons in the nucleus of an atom.
    [Show full text]
  • Some Problems Relating to Chain Reactions and to the Theory of Combustion
    N IKOLAI N . S E M E N O V Some problems relating to chain reactions and to the theory of combustion Nobel Lecture, December 11, 1956 I should like to report here on researches into the field of chemical kinetics and the processes of combustion conducted over the last 20-30 years, firstly in my laboratory at the Leningrad Physical-Technical Institute and then in the Institute of Chemical Physics in the Academy of Sciences. These re- searches represent the outcome of many years’ endeavours by a large group of scientific collaborators, many of whom have now become well-known authorities and leaders in individual branches of scientific learning. There can be no doubt that it is indeed thanks to the joint work, thanks to the continual mutual help, and at the same time thanks to the personal initiative of some members of our group that we succeeded in achieving the results which have been valued so highly here. Successful exchanges of views and friendly discussions with learned men in other countries, particularly with Sir Cyril Hinshelwood, contributed much to the development of these researches and, particularly in the initial stage, to the development of new ideas. From our own experience, we have come to the conclusion that only the joint activity of men of learning in various countries can create conditions under which science can achieve successful further development. Our investigations can be divided into two different groups, which are however closely linked with each other: (I) the application of chemical kinetics to problems relating to the theory of combustion and explosion processes; (2) the mechanism of chemical reactions, particularly chain reactions.
    [Show full text]
  • Chemical Kinetics 1.0 Objectives, Scope, Required Reading & Assignment Schedule
    Module 2: Chemical Kinetics 1.0 Objectives, Scope, Required Reading & Assignment Schedule Objectives By the end of this module, students should be able to: • Identify variables that influence the rate at which chemical reactions proceed • Compose a rate expression for a given reaction • Define simple and complex reactions • Understand the Arrhenius Rate Expression • Explain the difference between 1st, 2nd, and 3rd order reactions • Define chain reactions • Understand chain branching explosions • Understand the theory of homogeneous ignition of gases • Understand the Frank-Kamenetski analysis and how it can be utilized for understanding a materials propensity to self-heat and spontaneously ignite Scope • Analysis of chemical kinetics and reaction rates • Analysis of ignition pertaining to gases • Analysis of self-heating and spontaneous ignition Reading Assignments • Turns: Chapter 4 • Drysdale: Chapter 6.1, Chapter 8.1 Assignment Schedule Three problems worth 10 points total are to be completed and submitted online. There is also an extra credit problem available (4 points). See the last page of this module for more details. There are exercises within the module that should be attempted by the student, these will not count toward your grade. The discussion question in 6.1 (Self-heating) of the module will count towards your class participation grade. 2.0 Background In Module 1, we learned about the chemical thermodynamics that govern combustion. Thermodynamics determines equilibrium in a system and, therefore, establishes the direction Module 2: Chemical Kinetics that the system wants to go. For example, as we saw, thermodynamics determines adiabatic flame temperature, a limiting temperature that is virtually never achieved in practice.
    [Show full text]
  • Relativistic Runaway Electron Avalanches Within Complex Thunderstorm Electric field Structures
    Relativistic runaway electron avalanches within complex thunderstorm electric field structures E. Stadnichuka,b,∗, E. Svechnikovad, A. Nozika,e, D. Zemlianskayaa,c, T. Khamitova,c, M. Zelenyya,c, M. Dolgonosovb,f aMoscow Institute of Physics and Technology - 1 \A" Kerchenskaya st., Moscow, 117303, Russian Federation bHSE University - 20 Myasnitskaya ulitsa, Moscow 101000 Russia cInstitute for Nuclear Research of RAS - prospekt 60-letiya Oktyabrya 7a, Moscow 117312 dInstitute of Applied Physics of RAS - 46 Ul'yanov str., 603950, Nizhny Novgorod, Russia eJetBrains Research - St. Petersburg, st. Kantemirovskaya, 2, 194100 fSpace Research Institute of RAS, 117997, Moscow, st. Profsoyuznaya 84/32 Abstract Relativistic runaway electron avalanches (RREAs) are generally accepted as a source of thunderstorms gamma-ray radiation. Avalanches can multiply in the electric field via the relativistic feedback mechanism based on processes with gamma-rays and positrons. This paper shows that a non-uniform electric field geometry can lead to the new RREAs multiplication mechanism - \reactor feed- back", due to the exchange of high-energy particles between different accelerat- ing regions within a thundercloud. A new method for the numerical simulation of RREA dynamics within heterogeneous electric field structures is proposed. The developed analytical description and the numerical simulation enables us to derive necessary conditions for TGF occurrence in the system with the reactor feedback Observable properties of TGFs influenced by the proposed mechanism are discussed. Keywords: relativistic runaway electron avalanches, terrestrial gamma-ray flash, thunderstorm ground enhancement, gamma-glow, thunderstorm, arXiv:2105.02818v1 [physics.ao-ph] 6 May 2021 relativistic feedback, reactor feedback ∗Egor Stadnichuk Email address: [email protected] (E.
    [Show full text]
  • Lecture 18 Chain Reactions Nikolai Nikolaevic Semenov 1896-1986, Nobel 1956 Chain Reactions Are Examples of Complex Reactions, with Complex Rate Expressions
    Lecture 18 Chain reactions Nikolai Nikolaevic Semenov 1896-1986, Nobel 1956 Chain reactions are examples of complex reactions, with complex rate expressions. In a chain reaction, the intermediate produced in one step generates an intermediate in another step. This process goes on. Intermediates are called chain carriers. Sometimes, the chain carriers are radicals, they can be ions as well. In nuclear fission they are neutrons. There are several steps in a chain reaction. 1. Chain initiation This can be by thermolysis (heating) or photolysis (absorption of light) leading to the breakage of a bond. CH3CH3 Æ 2 CH3 2. Propagation In this the chain carrier makes another carrier. ⋅CH3 + CH3CH3 → CH4 + ⋅CH2CH3 3. Branching One carrier makes more than one carrier. ⋅O⋅ + H2O → HO⋅ + HO⋅ (oxygen has two unpaired electrons) 4. Retardation Chain carrier may react with a product reducing the rate of formation of the product. ⋅H + HBr → H2 + ⋅Br Retardation makes another chain carrier, but the product concentration is reduced. 5. Chain termination Radicals combine and the chain carriers are lost. ⋅ CH3CH2 + CH3CH2 → CH3CH2CH2CH3 6. Inhibition Chain carriers are removed by other processes, other than termination, say by foreign radicals. ⋅ ⋅ CH3CH2 + R → CH3CH2R All need not be there for a given reaction. Minimum necessary are, Initiation, propagation and termination. How do we account for the rate of laws of chain reactions? Look at the thermal decomposition of acetaldehyde. This appears to follow three-halves order in acetaldehyde. Overall reaction, 3/2 CH3CHO(g) → CH4(g) + CO(g) d[CH4]/dt = k[CH3CHO] The mechanism for this reaction known as Rice-Herzfeld mechanism is as follows.
    [Show full text]
  • The Physics of Nuclear Weapons
    The Physics of Nuclear Weapons While the technology behind nuclear weapons is of secondary importance to this seminar, some background is helpful when dealing with issues such as nuclear proliferation. For example, the following information will put North Korea’s uranium enrichment program in a less threatening context than has been portrayed in the mainstream media, while showing why Iran’s program is of greater concern. Those wanting more technical details on nuclear weapons can find them online, with Wikipedia’s article being a good place to start. The atomic bombs used on Hiroshima and Nagasaki were fission weapons. The nuclei of atoms consist of protons and neutrons, with the number of protons determining the element (e.g., carbon has 6 protons, while uranium has 92) and the number of neutrons determining the isotope of that element. Different isotopes of the same element have the same chemical properties, but very different nuclear properties. In particular, some isotopes tend to break apart or fission into two lighter elements, with uranium (chemical symbol U) being of particular interest. All uranium atoms have 92 protons. U-238 is the most common isotope of uranium, making up 99.3% of naturally occurring uranium. The 238 refers to the atomic weight of the isotope, which equals the total number of protons plus neutrons in its nucleus. Thus U-238 has 238 – 92 = 146 neutrons, while U-235 has 143 neutrons and makes up almost all the remaining 0.7% of naturally occurring uranium. U-234 is very rare at 0.005%, and other, even rarer isotopes exist.
    [Show full text]
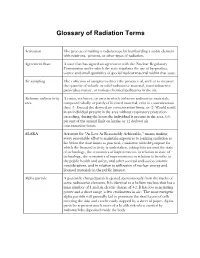
  • Glossary of Radiation Terms
    Glossary of Radiation Terms Activation The process of making a radioisotope by bombarding a stable element with neutrons, protons, or other types of radiation. Agreement State A state that has signed an agreement with the Nuclear Regulatory Commission under which the state regulates the use of by-product, source and small quantities of special nuclear material within that state. Air sampling The collection of samples to detect the presence of, and/or to measure the quantity of volatile or solid radioactive material, non-radioactive particulate matter, or various chemical pollutants in the air. Airborne radioactivity A room, enclosure, or area in which airborne radioactive materials, area composed wholly or partly of licensed material, exist in concentrations that: (1) Exceed the derived air concentration limits, or (2) Would result in an individual present in the area without respiratory protection exceeding, during the hours the individual is present in the area, 0.6 percent of the annual limit on intake or 12 derived air concentration-hours. ALARA Acronym for "As Low As Reasonably Achievable," means making every reasonable effort to maintain exposures to ionizing radiation as far below the dose limits as practical, consistent with the purpose for which the licensed activity is undertaken, taking into account the state of technology, the economics of improvements in relation to state of technology, the economics of improvements in relation to benefits to the public health and safety, and other societal and socioeconomic considerations, and in relation to utilization of nuclear energy and licensed materials in the public interest. Alpha particle A positively charged particle ejected spontaneously from the nuclei of some radioactive elements.
    [Show full text]
  • Reaction Kinetics
    1 Reaction Kinetics Dr Claire Vallance First year, Hilary term Suggested Reading Physical Chemistry, P. W. Atkins Reaction Kinetics, M. J. Pilling and P. W. Seakins Chemical Kinetics, K. J. Laidler Modern Liquid Phase Kinetics, B. G. Cox Course synopsis 1. Introduction 2. Rate of reaction 3. Rate laws 4. The units of the rate constant 5. Integrated rate laws 6. Half lives 7. Determining the rate law from experimental data (i) Isolation method (ii) Differential methods (iii) Integral methods (iv) Half lives 8. Experimental techniques (i) Techniques for mixing the reactants and initiating reaction (ii) Techniques for monitoring concentrations as a function of time (iii) Temperature control and measurement 9. Complex reactions 10. Consecutive reactions 11. Pre-equilibria 12. The steady state approximation 13. ‘Unimolecular’ reactions – the Lindemann-Hinshelwood mechanism 14. Third order reactions 15. Enzyme reactions – the Michaelis-Menten mechanism 16. Chain reactions 17. Linear chain reactions The hydrogen – bromine reaction The hydrogen – chlorine reaction The hydrogen-iodine reaction Comparison of the hydrogen-halogen reactions 18. Explosions and branched chain reactions The hydrogen – oxygen reaction 19. Temperature dependence of reaction rates The Arrhenius equation and activation energies Overall activation energies for complex reactions Catalysis 20. Simple collision theory 2 1. Introduction Chemical reaction kinetics deals with the rates of chemical processes. Any chemical process may be broken down into a sequence of one or more single-step processes known either as elementary processes, elementary reactions, or elementary steps. Elementary reactions usually involve either a single reactive collision between two molecules, which we refer to as a a bimolecular step, or dissociation/isomerisation of a single reactant molecule, which we refer to as a unimolecular step.
    [Show full text]
  • Physical Science Vocabulary
    PHYSICAL SCIENCE VOCABULARY acceleration- The rate of change in atomic nucleus; has a charge of 2+, an velocity (a change in direction or a atomic mass of 4, and is the largest, change in speed). slowest, and least penetrating form of acid- A substance that produces radiation. hydrogen ions in solution; these amalgam- An alloy containing the solutions have a pH less than 7. element mercury; an example is dental alternating current (AC) - Electric fillings. current that reverses its direction in a ammeter- A galvanometer that regular pattern; the 60-Hz AC in our measures electrical current passing homes changes direction 120 times each through in amperes; connected in a second. series with the circuit. acid rain - Rain with a pH less than 5.6; amorphous- Something that has no produced by substances in the air specific shape; for example, a liquid or reacting with rainwater. gas. acoustics -The study of sound. ampere -The unit of measuring current, actinide- Any of the 14 radioactive the rate of flow of electrons in a circuit. elements having atomic numbers 90- amplification- The process of increasing 103; used in nuclear power generation the strength of an electric signal. and nuclear weapons. amplitude- In a wave, the distance from active solar heating - Collecting the the rest position of the medium to either sun's energy with solar panels, heating the crest or trough. water with that energy, and storing the amplitude modulated - (AM) waves - heated water to use the energy later. Radio waves whose amplitude is varied aerosol -A liquid sprayed from a with voice, music, video, or data for pressurized container; for example, a can transmission over long distances.
    [Show full text]
  • Radicals in Flames
    RAD CALS • W. E. Wilson, Jr. and R. M. Fristrom In adicals are an essential chemical species in in a steady-state flame it is only necessary that R flames. Although present in low concentra­ chain branching balance chain breaking. tions, they are responsible for ignition and for the These species are so reactive that their lifetimes rapid reaction rates observed in flames. A radical are very short. It is necessary, therefore, to utilize is an atom or group of atoms, which, in chemical unusual techniques to study them. Cochran, terms, has a free valency and may react to form a Adrian, and Bowers~ in a recent article, discussed more stable molecule. Except for unusual cases or the use of liquid helium to stabilize at low tempera­ extreme environments, radicals may be considered ture radicals formed by ultraviolet photolysis. l as highly reactive, transient chemical species. Some The present paper will discuss the study of radicals of the important radicals in hydrogen and hydro­ in the high-temperature environment of flames. carbon flames are hydrogen atoms (H), hydroxyl Since the general problem of studying flames radicals (OH), oxygen atoms (0), and methyl has been discussed previously by Fristrom and radicals (CH3). Westenberg,2 only the determination of radicals in An illustration of how radicals enhance the rate flames and the application of these results to the of a reacting system may be had by examining the study of chemical kinetics will be considered here. hydrogen-oxygen flame. An undisturbed mixture of H 2 and O 2 is quite stable at room temperature.
    [Show full text]