Comparison of Observed (HF Radar and ADCP Measurements) and Computed Tides in the North Channel of the Irish Sea
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Impact of Sea-Level Rise on Tidal Characteristics Around Australia
The impact of sea-level rise on tidal characteristics around Australia ANGOR UNIVERSITY Harker, Alexander; Green, Mattias; Schindelegger, Michael; Wilmes, Sophie- Berenice Ocean Science DOI: 10.5194/os-2018-104 PRIFYSGOL BANGOR / B Published: 19/02/2019 Publisher's PDF, also known as Version of record Cyswllt i'r cyhoeddiad / Link to publication Dyfyniad o'r fersiwn a gyhoeddwyd / Citation for published version (APA): Harker, A., Green, M., Schindelegger, M., & Wilmes, S-B. (2019). The impact of sea-level rise on tidal characteristics around Australia. Ocean Science, 15(1), 147-159. https://doi.org/10.5194/os- 2018-104 Hawliau Cyffredinol / General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal ? Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. 07. Oct. 2021 Ocean Sci., 15, 147–159, 2019 https://doi.org/10.5194/os-15-147-2019 © Author(s) 2019. This work is distributed under the Creative Commons Attribution 4.0 License. -

The Impact of Sea-Level Rise on Tidal Characteristics Around Australia Alexander Harker1,2, J
The impact of sea-level rise on tidal characteristics around Australia Alexander Harker1,2, J. A. Mattias Green2, Michael Schindelegger1, and Sophie-Berenice Wilmes2 1Institute of Geodesy and Geoinformation, University of Bonn, Bonn, Germany 2School of Ocean Sciences, Bangor University, Menai Bridge, United Kingdom Correspondence: Alexander Harker ([email protected]) Abstract. An established tidal model, validated for present-day conditions, is used to investigate the effect of large levels of sea-level rise (SLR) on tidal characteristics around Australasia. SLR is implemented through a uniform depth increase across the model domain, with a comparison between the implementation of coastal defences or allowing low-lying land to flood. The complex spatial response of the semi-diurnal M2 constituent does not appear to be linear with the imposed SLR. The most 5 predominant features of this response are the generation of new amphidromic systems within the Gulf of Carpentaria, and large amplitude changes in the Arafura Sea, to the north of Australia, and within embayments along Australia’s north-west coast. Dissipation from M2 notably decreases along north-west Australia, but is enhanced around New Zealand and the island chains to the north. The diurnal constituent, K1, is found to decrease in amplitude in the Gulf of Carpentaria when flooding is allowed. Coastal flooding has a profound impact on the response of tidal amplitudes to SLR by creating local regions of increased tidal 10 dissipation and altering the coastal topography. Our results also highlight the necessity for regional models to use correct open boundary conditions reflecting the global tidal changes in response to SLR. -

Clockwise Phase Propagation of Semi-Diurnal Tides in the Gulf of Thailand
Journal of Oceanography, Vol. 54, pp. 143 to 150. 1998 Clockwise Phase Propagation of Semi-Diurnal Tides in the Gulf of Thailand 1 2 TETSUO YANAGI and TOSHIYUKI TAKAO 1Research Institute for Applied Mechanics, Kyushu University, Kasuga 816, Japan 2Department of Civil and Environmental Engineering, Ehime University, Matsuyama 790, Japan (Received 4 August 1997; in revised form 3 December 1997; accepted 6 December 1997) The phase of semi-diurnal tides (M and S ) propagates clockwise in the central part of Keywords: 2 2 ⋅ the Gulf of Thailand, although that of the diurnal tides (K1, O1 and P1) is counterclock- Clockwise wise. The mechanism of clockwise phase propagation of semi-diurnal tides at the Gulf of amphidrome, ⋅ natural oscillation, Thailand in the northern hemisphere is examined using a simple numerical model. The ⋅ natural oscillation period of the whole Gulf of Thailand is near the semi-diurnal period tide, ⋅ Gulf of Thailand. and the direction of its phase propagation is clockwise, mainly due to the propagation direction of the large amplitude part of the incoming semi-diurnal tidal wave from the South China Sea. A simplified basin model with bottom slope and Coriolis force well reproduces the co-tidal and co-range charts of M2 tide in the Gulf of Thailand. 1. Introduction phase propagation of semi-diurnal tides at the Gulf of It is well known that the phase of tides propagates Thailand in the northern hemisphere using a simple numeri- counterclockwise (clockwise) in gulfs or shelf seas such as cal model. the North Sea, the Baltic, the Adria, the Persian Gulf, the Yellow Sea, the Sea of Okhotsk, the Gulf of Mexico and so 2. -

Lecture 1: Introduction to Ocean Tides
Lecture 1: Introduction to ocean tides Myrl Hendershott 1 Introduction The phenomenon of oceanic tides has been observed and studied by humanity for centuries. Success in localized tidal prediction and in the general understanding of tidal propagation in ocean basins led to the belief that this was a well understood phenomenon and no longer of interest for scientific investigation. However, recent decades have seen a renewal of interest for this subject by the scientific community. The goal is now to understand the dissipation of tidal energy in the ocean. Research done in the seventies suggested that rather than being mostly dissipated on continental shelves and shallow seas, tidal energy could excite far traveling internal waves in the ocean. Through interaction with oceanic currents, topographic features or with other waves, these could transfer energy to smaller scales and contribute to oceanic mixing. This has been suggested as a possible driving mechanism for the thermohaline circulation. This first lecture is introductory and its aim is to review the tidal generating mechanisms and to arrive at a mathematical expression for the tide generating potential. 2 Tide Generating Forces Tidal oscillations are the response of the ocean and the Earth to the gravitational pull of celestial bodies other than the Earth. Because of their movement relative to the Earth, this gravitational pull changes in time, and because of the finite size of the Earth, it also varies in space over its surface. Fortunately for local tidal prediction, the temporal response of the ocean is very linear, allowing tidal records to be interpreted as the superposition of periodic components with frequencies associated with the movements of the celestial bodies exerting the force. -
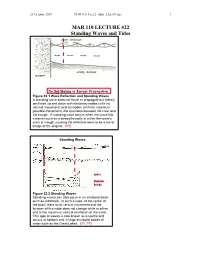
MAR 110 LECTURE #22 Standing Waves and Tides
23 October 2007 MAR110_Lec22_tides_23oct07.doc 1 MAR 110 LECTURE #22 Standing Waves and Tides No Net Motion or Energy Propagation Figure 22.1 Wave Reflection and Standing Waves A standing wave does not travel or propagate but merely oscillates up and down with stationary nodes (with no vertical movement) and antinodes (with the maximum possible movement) that oscillates between the crest and the trough. A standing wave occurs when the wave hits a barrier such as a seawall exactly at either the wave’s crest or trough, causing the reflected wave to be a mirror image of the original. (??) Standing Waves and a Bathtub Seiche Figure 22.2 Standing Waves Standing waves can also occur in an enclosed basin such as a bathtub. In such a case, at the center of the basin there is no vertical movement and the location of this node does not change while at either end is the maximum vertical oscillation of the water. This type of waves is also known as a seiche and occurs in harbors and in large enclosed bodies of water such as the Great Lakes. (??, ??) 23 October 2007 MAR110_Lec22_tides_23oct07.doc 2 Standing Wave or Seiche Period l Figure 22.3 The wavelength of a standing wave is equal to twice the length of the basin it is in, which along with the depth (d) of the water within the basin, determines the period (T) of the wave. (ItO) Standing Waves & Bay Tides l Figure 22.4 Another type of standing wave occurs in an open basin that has a length (l) one quarter that of the wave in this case, usually a tide. -

Causes of Tides – Tutorial Script in the First Video Tutorial of This Series, We Studied Tidal Data from Many Locations Worldwide and Learned How Tides Behave
Causes of Tides – Tutorial Script In the first video tutorial of this series, we studied tidal data from many locations worldwide and learned how tides behave. In this video tutorial, we will explore the causes of that behavior. First of all, we know that most tidal waves have a period of one wave every 12 hrs and 25 minutes otherwise stated as two waves every 24 hrs and 50 minutes. What else has that same period? Earth’s rotation relative to the Moon is also 24 hours and 50 minutes. What does that mean? After the Earth has rotated once relative to the Sun – 24 hours – it has to rotate another 50 minutes to catch up with the Moon, which during that 24 hours moved 1/29th its way around its orbit around the Earth. 24 hours and 50 minutes is a lunar day. In addition, the two week cycle of neap and spring tides exactly matches the phases of the Moon as the Moon completes its orbit around the Earth. The Moon is the main agent causing tides on our planet. How? This image, which is not to scale, shows a spherical blue Earth that is being pulled to the right by a gravitational force between itself and the Moon. The side of Earth closest to the Moon has a longer arrow, representing the stronger gravitational force felt there. The arrow on the opposite side is shorter because its force is smaller. Gravitational force is stronger, the closer two objects are together and weaker, the further away they are. -

Seiches in the Semiclosed Seas of the Continental Shelf
International Journal of Oceanography & Aquaculture MEDWIN PUBLISHERS ISSN: 2577-4050 Committed to Create Value for Researchers Seiches in the Semiclosed Seas of the Continental Shelf Inzhebeikin Yu I* Research Article Russian Academy of Sciences, Russia Volume 4 Issue 3 Received Date: September 18, 2020 *Corresponding author: Published Date: October 23, 2020 Center, Rostov-on-Don, Russia, Email: [email protected] Inzhebeikin Yu I, Russian Academy of Sciences, Southern Scientific DOI: 10.23880/ijoac-16000199 Abstract Seiche movements in two small areas of semi-closed seas on the Continental Shelf (the White Sea and the Sea of Azov) with very different morphometric characteristics are considered in this paper. In addition, tidal movements are highly developed in the White sea, while in the Azov sea tides are virtually absent. We’ve used morphometric characteristics of the seas, including the ones recently obtained by the Azov Sea, as well as methods of numerical hydrodynamic simulation based on the theory of shallow water, and spectral analysis of the observation data of the sea level fluctuations. Keywords: Continental Shelf; Semi-Closed Seas; White Sea; Sea Of Azov; Seiche; Numerical Hydrodynamic Simulation; Spectral Analysis; Flood Introduction located in the Northern and South-Western boundaries of the European part of Russia respectively (Figure 1). In August 2006, on the Dolzhanskaya spit of the Azov sea, the water level rose sharply, people and cars washed away in the sea, the spit broke in several places. At the same time there was no storm warning. In June 2010 on the Yeisk spit of the same sea of Azov at full calm across the sea suddenly appeared powerful current washed away children, wandering on the spit knee-deep in water. -

The Two-Dimensional Seiches of the Baltic Sea
_____________________________________o_c_E_A_N_O_L_O_G_IC_A_A_C_T_A __ 19_7_9_-_v_o_L_._2_-_N_o_4 __ ~------ Two-dimensional seiches Numerical solution The two-dimensional seiches Baltic Sea Oscillations bidimensionnelles Solution numérique of the Bal tic Sea · Mer Baltique Ch. Wübber, W. Krauss Institut für Meereskunde, Düsternbrooker Weg 20, 23/Kiel, RFA. Received 6/4/79, in revised form 22/6/79, accepted 2/7/79. ABSTRACT Periods and structures of the gravitational free oscillations in the Baltic Sea are determined from theoretical calculations. The calculations take into account the bathymetry and shape of the Baltic and the earth's rotation. The method for determining the free oscilla tions is based on a difference approximation of the inviscid quasistatic shallow water equations. The seiches are produced by a forcing function which acts on the water body during an initial time. The resulting oscillations after the force is switched off are analyzed at each grid point and displayed in form of co-range and co-tidallines. The calculations were carried out for the entire Baltic Sea and for the Baltic proper. A large variety of oscillations is possible. The results are compared with those of the channel theory. It is shown that the eigenoscillations of the Baltic Sea are strongly modified by the Coriolis force. Rotation couverts all modes into positive amphidromic waves; only the interior parts of the Gulfs and of the Western Baltic exhibit standing waves. The periods of the oscillations are reduced by earth rotation, if they are longer than the inertial period, and prolongated, in case they are shorter. The Gulf of Riga, neglected in computations based on channel theory, is of considerable importance for the seiches of the Baltic Sea. -

Influence of Potential Future Sea-Level Rise on Tides in The
Journal of Coastal Research 00 0 000–000 Coconut Creek, Florida Month 0000 Influence of Potential Future Sea-Level Rise on Tides in the China Sea Cuiping Kuang†*, Huidi Liang†, Xiaodan Mao†, Bryan Karney‡, Jie Gu§, Hongcheng Huang†, Wei Chen†, and Honglin Song† †College of Civil Engineering ‡College of Civil Engineering §College of Marine Sciences Tongji University University of Toronto Shanghai Ocean University Shanghai 200092, China Toronto M5S 1A4, Canada Shanghai 201306, China ABSTRACT Kuang, C.; Liang, H.; Mao, X.; Karney, B.; Gu, J.; Huang, H.; Chen, W., and Song, H., 0000. Influence of potential future sea-level rise on tides in the China Sea. Journal of Coastal Research, 00(0), 000–000. Coconut Creek (Florida), ISSN 0749-0208. This study investigates the diurnal and semidiurnal tidal responses of the entire China Sea to a potential rise in sea level of 0.5–2 m. A modified two-dimensional tidal model based on MIKE21 is primarily configured and validated for the present situation; then, three (0.5, 1, 2 m) sea-level rise (SLR) scenarios are simulated with this model. The predicted results show that the principal lunar semidiurnal (M2) and diurnal (K1) tidal constituents respond to SLR in a spatially nonuniform manner. Generally, changes of M2 and K1 amplitudes in shallow waters are larger than those in the deep sea, and significant tidal alterations mainly occur in the Bohai and Yellow seas, Jianghua Bay, Hangzhou Bay, Taiwan Strait, Yangtze River estuary, Pearl River estuary, and Beibu Bay. Possible mechanisms further discussed for these changes mainly relate to bottom friction decreasing, amphidromic point migration, and resonant effect change. -

The Impact of Sea-Level Rise on Tidal Characteristics Around Australasia Alexander Harker1,2, J.A
Ocean Sci. Discuss., https://doi.org/10.5194/os-2018-104 Manuscript under review for journal Ocean Sci. Discussion started: 6 September 2018 c Author(s) 2018. CC BY 4.0 License. The impact of sea-level rise on tidal characteristics around Australasia Alexander Harker1,2, J.A. Mattias Green2, and Michael Schindelegger1 1Institute of Geodesy and Geoinformation, University of Bonn, Bonn, Germany 2School of Ocean Sciences, Bangor University, Menai Bridge, United Kingdom Correspondence: Alexander Harker ([email protected]) Abstract. An established tidal model, validated for present-day conditions, is used to investigate the effect of large levels of sea-level rise (SLR) on tidal characteristics around Australasia. SLR is implemented through a uniform depth increase across the model domain, with a comparison between the coastal boundary being treated as impenetrable or allowing low-lying land to flood. The complex spatial response of the semi-diurnal constituents, M2 and S2, is broadly similar, with the magnitude of 5 M2’s response being greater. The most predominant features of this response are large amplitude changes in the Arafura Sea and within embayments along Australia’s north-west coast, and the generation of new amphidromic systems within the Gulf of Carpentaria and south of Papua, once water depth across the domain is increased by 3 and 7 m respectively. Dissipation from M2 increases around the islands in the north of the Sahul shelf region and around coastal features along north Australia, leading to a notable drop in dissipation along Eighty Mile Beach. The diurnal constituent, K1, is found to be amplified within the Gulf 10 of Carpentaria, indicating a possible change of resonance properties of the gulf. -

On the Tidal Dynamics of the North Sea
ON THE TIDAL DYNAMICS OF THE NORTH SEA An idealised modelling study on the role of bottom friction, the Dover Strait and tidal resonance in the North Sea. Enschede, 17 September 2010. ThiThiss master thesis was written by Jorick J. Velema BSc. aaasas fulfilment of the Master’s degree Water Engineering & Management, University of Twente, The Netherlands uuunderunder the supervision of the following committee Daily supervisor: Dr. ir. P.C. Roos (University of Twente) Graduation supervisor: Prof. dr. S.J.M.H. Hulscher (University of Twente) External supervisor: Drs. A. Stolk (Rijkswaterstaat Noordzee) Abstract This thesis is a study on the tidal dynamics of the North Sea, and in particular on the role of bottom friction, the Dover Strait and tidal resonance in the North Sea. The North Sea is one of the world’s largest shelf seas, located on the European continent. There is an extensive interest in its tide, as coastal safety, navigation and ecology are all affected by it. The tide in the North Sea is a co-oscillating response to the tides generated in the North Atlantic Ocean. Tidal waves enter the North Sea through the northern boundary with the North Atlantic Ocean and through the Dover Strait. Elements which play a possible important role on the tidal dynamics are bottom friction, basin geometry, the Dover Strait and tidal resonance. The objective of this study is to understand the large-scale amphidromic system of the North Sea, and in particular (1) the role of bottom friction, basin geometry and the Dover Strait on North Sea tide and (2) the resonant properties of the Southern Bight . -

Coastal Erosion
INTEGRATED FLOOD MANAGEMENT TOOLS SERIES COASTAL AND DELTA FLOOD MANAGEMENT ISSUE 17 MAY 2013 The Associated Programme on Flood Management (APFM) is a joint initiative of the World Meteorological Organization (WMO) and the Global Water Partnership (GWP). It promotes the concept of Integrated Flood Management (IFM) as a new approach to flood management. The programme is financially supported by the governments of Japan, Switzerland and Germany. www.floodmanagement.info The World Meteorological Organization is a Specialized Agency of the United Nations and represents the UN-System’s authoritative voice on weather, climate and water. It co-ordinates the meteorological and hydrological services of 189 countries and territories. www.wmo.int The Global Water Partnership is an international network open to all organizations involved in water resources management. It was created in 1996 to foster Integrated Water Resources Management (IWRM). www.gwp.org Integrated Flood Management Tools Series No.17 © World Meteorological Organization, 2013 Cover photo: Westkapelle, Netherlands Layout, design and iconography : www.lamenagerie.net To the reader This publication is part of the “Flood Management Tools Series” being compiled by the Associated Programme on Flood Management. The “Coastal and Delta Flood Management” Tool is based on available literature, and draws findings from relevant works wherever possible. This Tool addresses the needs of practitioners and allows them to easily access relevant guidance materials. The Tool is considered as a resource guide/material for practitioners and not an academic paper. References used are mostly available on the Internet and hyperlinks are provided in the References section. This Tool is a “living document” and will be updated based on sharing of experiences with its readers.