The Circle Method and Bounds for L-Functions - IV: Subconvexity for Twists of GL(3) L-Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
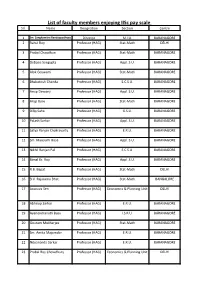
List of Faculty Members Enjoying Iisc Pay Scale Srl
List of faculty members enjoying IISc pay scale Srl. Name Designation Section Centre 1 Sm. Sanghamitra Bandyopadhyay Director M.I.U. BARANAGORE 2 Rahul Roy Professor (HAG) Stat-Math DELHI 3 Probal Chaudhuri Professor (HAG) Stat-Math BARANAGORE 4 Debasis Sengupta Professor (HAG) Appl. S.U. BARANAGORE 5 Alok Goswami Professor (HAG) Stat-Math BARANAGORE 6 Bhabatosh Chanda Professor (HAG) E.C.S.U. BARANAGORE 7 Anup Dewanji Professor (HAG) Appl. S.U. BARANAGORE 8 Arup Bose Professor (HAG) Stat-Math BARANAGORE 9 Dilip Saha Professor (HAG) G.S.U. BARANAGORE 10 Palash Sarkar Professor (HAG) Appl. S.U. BARANAGORE 11 Satya Ranjan Chakravarty Professor (HAG) E.R.U. BARANAGORE 12 Sm. Mausumi Bose Professor (HAG) Appl. S.U. BARANAGORE 13 Nikhil Ranjan Pal Professor (HAG) E.C.S.U. BARANAGORE 14 Bimal Kr. Roy Professor (HAG) Appl. S.U. BARANAGORE 15 R.B. Bapat Professor (HAG) Stat-Math DELHI 16 B.V. Rajarama Bhat Professor (HAG) Stat-Math BANGALORE 17 Arunava Sen Professor (HAG) Economics & Planning Unit DELHI 18 Abhirup Sarkar Professor (HAG) E.R.U. BARANAGORE 19 Ayanendranath Basu Professor (HAG) I.S.R.U. BARANAGORE 20 Goutam Mukherjee Professor (HAG) Stat-Math BARANAGORE 21 Sm. Amita Majumder Professor (HAG) E.R.U. BARANAGORE 22 Nityananda Sarkar Professor (HAG) E.R.U. BARANAGORE 23 Prabal Roy Chowdhury Professor (HAG) Economics & Planning Unit DELHI 24 Subhamoy Maitra Professor (HAG) Appl. S.U. BARANAGORE 25 Tapas Samanta Professor (HAG) Appl. S.U. BARANAGORE 26 Abhay Gopal Bhatt Professor (HAG) Stat-Math DELHI 27 Atanu Biswas Professor (HAG) Appl. S.U. -

Infosys Prize 2017
Infosys Science Foundation INFOSYS PRIZE 2017 The Romanesco broccoli has fascinated photographers the world over. The brilliant chartreuse and the mesmerizing spiral spines belong to an edible flower bud of the species Brassica oleracea. Grown in Italy since the 16th century, this broccoli- cauliflower hybrid is nutritionally rich, with a delicate nutty flavor. Romanesco thus demands as much interest from chefs as from botanists and researchers. But it doesn’t stop there – peer closely and you will see just how incredible it really is. For it is one of the earth’s most stunning natural fractals. In other words, each of its buds is composed of a series of smaller buds, all arranged in yet another logarithmic spiral. The same pattern continues at several diminishing size levels. Studies of fractals found in nature, such as a snowflake or lightning bolts or indeed the Romanesco broccoli, trace a path to modern applications in computer graphics. We tend to divide and study distinct subjects – physics, biology, math, engineering and so on – only to find one interconnected universe. And it gets even more bizarre. The number of spirals on the head of a Romanesco broccoli is a natural approximation of the Fibonacci number. Named after the Italian mathematician, the Fibonacci spiral is a logarithmic spiral where every quarter turn is farther from the origin by a factor of phi, the golden ratio. How about that for a little bit of math in your soup? ENGINEERING AND COMPUTER SCIENCE The Infosys Prize 2017 in Engineering and Computer Science is awarded to Prof. Sanghamitra Bandyopadhyay for her scholarly record in algorithmic optimization and for its significant impact on biological data analysis. -

A Celebration of Mathematics 2018 Ramanujan Prize Award
SRINIVASA RAMANUJAN A CELEBRATION OF MATHEMATICS Srinivasa Ramanujan was born in 1887 in Erode, Tamil Nadu, India. He grew up in poverty and hardship. Ramanujan was unable to pass his school examinations, and could only obtain a clerk’s position in the city of Madras. 2018 RAMANUJAN PRIZE However, he was a genius in pure mathematics and essentially self-taught from a single text book that was available to him. He continued to pursue AWARD CEREMONY his own mathematics, and sent letters to three mathematicians in England, containing some of his results. While two of the three returned the letters unopened, G.H. Hardy recognized Ramanujan’s intrinsic mathematical ability and arranged for him to go to Cambridge. Hardy was thus responsible for ICTP making Ramanujan’s work known to the world during the latter’s own lifetime. Ramanujan made spectacular contributions to elliptic functions, continued 9 November 2018 fractions, infinite series, and analytical theory of numbers. His health deteriorated rapidly while in England. He was sent home to recuperate in 1919, but died the next year at the age of 32. RAMANUJAN PRIZE In 2005 the Abdus Salam International Centre for Theoretical Physics (ICTP) established the Srinivasa Ramanujan Prize for Young Mathematicians from Developing Countries, named after the mathematics genius from India. This Prize is awarded annually to a mathematician under 45. Since the mandate of ICTP is to strengthen science in developing countries, the Ramanujan Prize has been created for mathematicians from developing countries. Since Ramanujan is the quintessential symbol of the best in mathematics from the developing world, naming the Prize after him seemed entirely appropriate. -

B3-I School of Mathematics (Math)
B3-I School of Mathematics (Math) Evaluative Report of Departments (B3) I-Math-1 School of Mathematics 1. Name of the Department : School of Mathematics (Math) 2. Year of establishment : 1945 3. Is the Department part of a School/Faculty of the university? It is an entire School. 4. Names of programmes offered (UG, PG, M.Phil., Ph.D., Integrated Masters; Integrated Ph.D., D. Sc, D. Litt, etc.) 1. Ph.D. 2. Integrated M.Sc.-Ph.D. The minimum eligibility criterion for admission to the Ph.D. programme is a Master's degree in any of Mathematics/Statistics/Science/Technology (M.A. / M.Sc. / M. Math / M. Stat / M.E. / M. Tech.). The minimum eligibility criterion for admission to the Integrated Ph.D. programme is a Bachelor's degree in any of Mathematics/Statistics/Science/Technology (B.A. / B.Sc. / B. Math. / B. Stat. / B.E. / B. Tech.). Students without a Master's degree will generally be admitted to the Integrated Ph.D. program and will obtain an M.Sc. degree along the way subject to the completion of all requirements. Students with a four-year Bachelor's degree may be considered for admission to the Ph.D. Programme. 5. Interdisciplinary programmes and departments involved None 6. Courses in collaboration with other universities, industries, foreign institutions, etc. None TIFR NAAC Self-Study Report 2016 I-Math-2 Evaluative Report of Departments (B3) 7. Details of programmes discontinued, if any, with reasons There are no such programmes. 8. Examination System: Annual/Semester/Trimester/Choice Based Credit System There is an evaluation at the end of each semester course, based on assignments and written examinations, and an annual evaluation of courses based on an interview. -

(Ecole Polytechnique, Palaiseau, France) Yves Andre
PARTICIPANTS Emiliano Ambrosi (Ecole Polytechnique, Palaiseau, France) Yves Andre (CNRS, Paris, France) Dario Antolini (University of Rome, Italy) Stanislav Atanasov (Columbia University, NY, USA) Gregorio Baldi (University College London, UK) Jennifer Balakrishnan (Boston University, USA) Raphael Beuzart-Plessis (Institut de Mathematiques de Marseille, France) Fabrizio Barroero (Universit degli Studi Roma Tre, Italy) Florian Breuer (University of Newcastle, Australia) Anna Cadoret (Jussieu, Paris) Laura Capuano (University of Oxford, UK) Bumkyu Cho (Dongguk University, Seoul, South Korea) Kevin Kwan Chung (Columbia University, NY, USA) Giovanni Coppola (University of Salerno, Italy) Pietro Corvaja (University of Udine, Italy) Henri Darmon (McGill University, Montreal, Canada) Christopher Daw (University of Reading, UK) Alexis (Suki) Dasher (University of Minnesota, USA) Julian Lawrence Demeio (Scuola Normale Superiore, Pisa, Italy) Daniel Disegni (Ben Gurion University, Israel) Ick Sun Eum ( Dongguk University, Gyeongju City, South Korea) Rita Eppler-Goss (Ohio, USA) Bernadette Faye (Universite Cheikh Anta Diop De Dakar, Senegal) Ziyang Gao (Princeton University, USA) Michel Giacomini (University College, London, UK) Dorian Goldfeld (Columbia University, NY, USA) Giada Grossi (University College London, UK) Akash Jena (Indiana University, Bloomington, USA) Boris Kadets (MIT, Cambridge MA, USA) Sudesh Kaur Khanduja (IISER, Punjab, India) Ilya Khayutin (Princeton University, USA) Seema Kushwaha (Harish-Chandra Research Institute, Prayagraj, -

Chennai Mathematical Institute Annual Report 2009 - 2010 75 76 Chennai Mathematical Institute
Chennai Mathematical Institute Annual Report 2009 - 2010 H1, SIPCOT IT Park Padur Post, Siruseri, Tamilnadu 603 103. India. Chennai Mathematical Institute H1, SIPCOT IT Park Padur Post, Siruseri, Tamilnadu 603 103. India. Tel: +91-44-2747 0226 - 0229 +91-44-3298 3441 - 3442 Fax: +91-44-2747 0225 WWW: http://www.cmi.ac.in Design and Printing by: Balan Achchagam, Chennai 600 058 Contents 1. Preface ................................................................................................................... 5 2. Board of Trustees ................................................................................................. 9 3. Governing Council ............................................................................................. 10 4. Research Advisory Committee .......................................................................... 11 5. Academic Council ............................................................................................... 12 6. Boards of Studies ................................................................................................ 13 7. Institute Members ............................................................................................. 14 8. Faculty Profiles ................................................................................................... 17 9. Awards ................................................................................................................. 25 10. Research Activities ............................................................................................ -
Academic Review
ACADEMIC REVIEW for the period April 2011 { January 2016 Department of Mathematics Indian Institute of Science Bangalore February 08, 2016 Contents 1 About the Department 1 1.1 Institute and Department background ................... 1 1.2 Scientific Staff in the Department ...................... 2 1.2.1 Faculty .................................... 2 1.2.2 UGC Research Scientist ........................... 3 1.2.3 Emeritus Scientists ............................. 3 1.2.4 NMI Distinguished Associate ........................ 3 1.2.5 MO Cell Faculty .............................. 4 1.2.6 INSPIRE Fellows/DST Young Scientists .................. 4 1.2.7 Post Doctoral Fellows/Research Associates ................ 4 1.2.8 Students ................................... 6 1.2.9 Visiting Students .............................. 11 2 Center for Advanced Study 12 2.1 Faculty involved ................................. 12 2.1.1 In the identified thrust area . 12 2.1.2 In other area . 12 3 Major achievements 13 3.1 Teaching ...................................... 13 3.2 Research ...................................... 18 3.2.1 Research Highlights in Thrust area ..................... 18 3.2.2 Research Highlights in other areas ..................... 34 3.2.3 Publications ................................. 44 3.3 Human resource training ........................... 67 3.3.1 The National Mathematics Initiative (NMI) . 67 3.3.2 Mathematical Olympiad ........................... 68 3.3.3 Olympiad training camps .......................... 69 3.3.4 Visiting summer students -
Volume 1. No.1 (2015)
TIFR Alumni Association December 2015 December TAA Newsletter IN THIS ISSUE Editor’s Message From the Patron’s Desk TAA President’s Message Public Lectures Prof. Amit Roy Interviews Awards and Honors TIFR News Contributory Articles Prof. J.N. Goswami Prof. P.C. Agrawal Prof. Jayant Narlikar 1 Editor’s Message Enjoy Reading! We are happy to bring to our TAA mem- bers this year's TAA Newsletter "SAMPARK". The online edition has gained excellent popularity among read- ers since 2008. As in the earlier editions, this year's Newsletter too has public lec- tures by distinguished alumni and their Dr. R. S. Chaughule interviews on their work at TIFR and [email protected] personal life. Ex. Tata Institute of Fund. Research Adjunct Professor Ramnarain Ruia College We are happy to note that the TAA mem- Mumbai bership is increasing due to students' en- rollment. For updates please read our portal TAA- Red.com Happy reading Dr. Sangita Bose [email protected] UM-DAE Center for Excellence in Basic Sciences, (CEBS) Mumbai ---------------------------------------------------- Acknowledgement We thank Mr. Mohan Kakade, TAA Admn. Secretary for his efforts in designing this newsletter. 2 From the Patron’s Desk The TAA has been active in the organi- zation of Public Lectures, interviewing some of the distinguished speakers, recognizing the work of distinguished alumni through TAA Excellence awards and recognizing the students for their exemplary performance in their doc- toral work. The special Cowsik awards have had exceptional works of young scientists being recognized. This year, I am happy to note, that the TAA has introduced the award for Excellence in Teaching, and that four eminent scientists have been chosen in the field of Biology and Physics for this award. -

PM Ushers in CSIR's Platinum Jubilee Function
ISSN 0409-7467 CSIR News NEWSLETTER OF THE COUNCIL OF SCIENTIFIC & INDUSTRIAL RESEARCH Volume 66 No. 19 & 20 website: http://www.csir.res.in October 2016 In This Issue In The News CSIR’s Platinum Jubilee Function at Vigyan Bhawan 217 In The News • PM Ushers in CSIR’s Platinum Jubilee Function – Applauds PM Ushers in CSIR’s Platinum Jubilee CSIR for Leaving Indelible Mark Function – Applauds CSIR for Leaving Indelible Mark 226 Shanti Swarup Bhatnagar Prize For Science & Technology 231 CSIR Young Scientist Awards 233 CSIR Technology Awards 2016 236 CSIR Award for S&T Innovations for Rural Development (CAIRD) CSIR Diamond Jubilee 238 THE Prime Minister of India Shri CSIR laboratories to the nation Technology Award Narendra Modi ushered in CSIR’s at a function held in Vigyan Bhawan in New Delhi. G N Ramachandran Gold Platinum Jubilee Celebrations on 240 An exclusive exhibition of Medal For Excellence in 26 September 2016 with a lively major technological contributions Biological Sciences & interaction with farmers from of CSIR was organised for the Technology 2016 five different locations across the country. The Prime Minister, benefit of the PM. The exhibits 240 CSIR Innovation Award who is also the President of showcased some of the most for School Children 2016 the Council of Scientific and stellar achievements of CSIR Industrial Research (CSIR), including the ones that are in dedicated seven new varieties of the pipeline and have great medicinal plants developed by potential of delivery to remove CSIR News OCTOBER 2016 217 CSIR Platinum Jubilee Function Vignettes of the exhibition the drudgery of the common masses, scented Geranium, aromatic grass largely in the areas of healthcare, Citronella, Lemongrass, flowering plant water conservation, solid waste Lily and ornamental flower plant Gerbera management, waste-to-wealth, developed by CSIR labs. -

Prof. Ritabrata Munshi Prof
50th ANNUAL CONVOCATION 2019 GUEST OF HONOUR Prof. Ritabrata Munshi Prof. Ritabrata Munshi received his undergraduate by the Department of Science and Technology, and early graduate education at the Indian Statistical Government of India in 2012. He is the recipient of Institute, Kolkata. He pursued his doctoral studies many awards including the Birla Science Prize in at Princeton University in the US with Prof. Andrew 2013, and the Shanti Swarup Bhatnagar Prize for Wiles. After receiving his Ph.D., he spent a few post- Science and Technology, the highest science award doctoral years in the US before returning to India in India, for the year 2015 in mathematical science to join the Tata Institute of Fundamental Research. category. He was elected a Fellow of the Indian Currently, he is affiliated to Indian Statistical Institute, Academy of Sciences in 2016. For his outstanding Kolkata. contributions to analytic aspects of number theory, he Prof. Munshi has been internationally recognized was awarded the Infosys Prize 2017 in Mathematical for his outstanding contributions to analytic number Sciences. He was awarded the ICTP Ramanujan theory. He has worked across the breadth of analytic Prize in 2018. He has been recognized for his work number theory, ranging from applying analytic number with an invited lecture at the International Congress theory to Diophantine problems, to making remarkable of Mathematicians 2018 which was held at Rio, Brazil. progress in modern analytic number theory related to He serves in the editorial board of The Journal of the L-functions arising from automorphic forms. Ramanujan Mathematical Society and the Hardy- He was awarded the Mark Swarna-Jayanti fellowship Ramanujan journal. -
![Arxiv:1710.02354V1 [Math.NT] 6 Oct 2017 Ymti Qaelf and Lift Square Symmetric 2]De O Eyo Hsdlct Feature](https://docslib.b-cdn.net/cover/8513/arxiv-1710-02354v1-math-nt-6-oct-2017-ymti-qaelf-and-lift-square-symmetric-2-de-o-eyo-hsdlct-feature-8538513.webp)
Arxiv:1710.02354V1 [Math.NT] 6 Oct 2017 Ymti Qaelf and Lift Square Symmetric 2]De O Eyo Hsdlct Feature
A NOTE ON BURGESS BOUND RITABRATA MUNSHI Abstract. Let f be a SL(2, Z) Hecke cusp form, and let χ be a primitive Dirichlet character modulo M, which we assume to be prime. We prove the Burgess type bound for the twisted L-function: L 1 ,f χ M 1/2−1/8+ε. 2 ⊗ ≪f,ε The method also yields the original bound of Burgess for Dirichlet L- functions: L 1 ,χ M 1/4−1/16+ε. 2 ≪ε 1. Introduction In the series of papers [15], [16], [17], [18] and [20] a new approach to prove subconvexity has been proposed. This method has turned out to be quite effective in the case of degree three L-functions. Indeed if π is a SL(3, Z) Hecke-Maass cusp form then the t aspect subconvex bound L( 1 + it, π) (2 + t )3/4−1/16+ε, 2 ≪ | | was established in [17], and if χ is a primitive Dirichlet character modulo a prime M, then the twist aspect subconvex bound L( 1 , π χ) M 3/4−1/308+ε, 2 ⊗ ≪ was established in [18] and [20]. In the special case, where π is a symmetric square lift of a SL(2, Z) form, then the former bound was previously obtained by Li [13], building on the work of Conrey and Iwaniec [8]. Again for π a arXiv:1710.02354v1 [math.NT] 6 Oct 2017 symmetric square lift and χ a quadratic character, a subconvex bound (with a much stronger exponent) in the latter case was previously obtained by Blomer [2]. -

Yearbook-2020-USE This.Indd
NAL SCIEN IO CE T A A C N A N D A E I M D Y N I Year Book of The Indian National Science Academy 2020 Volume I Fellows 2020 i The Year Book 2020 Volume–I S NAL CIEN IO CE T A A C N A N D A E I M D Y N I INDIAN NATIONAL SCIENCE ACADEMY New Delhi ii The Year Book 2020 © INDIAN NATIONAL SCIENCE ACADEMY ISSN 0073-6619 E-mail : esoffi [email protected], [email protected] Fax : +91-11-23231095, 23235648 EPABX : +91-11-23221931-23221950 (20 lines) Website : www.insaindia.res.in; www.insa.nic.in (for INSA Journals online) INSA Fellows App: Downloadable from Google Play store Vice-President (Publications/Informatics) Professor Gadadhar Misra, FNA Production Dr Sudhanshu Aggarwal Shruti Sethi Published by Professor Gadadhar Misra, Vice-President (Publications/Informatics) on behalf of Indian National Science Academy, Bahadur Shah Zafar Marg, New Delhi 110002 and printed at Angkor Publishers (P) Ltd., B-66, Sector 6, NOIDA-201301; Tel: 0120-4112238 (O); 9910161199, 9871456571 (M) Fellows 2020 iii CONTENTS Volume–I Page INTRODUCTION ....... v OBJECTIVES ....... vi CALENDAR ....... vii COUNCIL ....... ix PAST PRESIDENTS OF THE ACADEMY ....... xi RECENT PAST VICE-PRESIDENTS OF THE ACADEMY ....... xii SECRETARIAT ....... xiv THE FELLOWSHIP Fellows – 2020 ....... 1 Foreign Fellows – 2020 ....... 158 Pravasi Fellows – 2020 ....... 176 Fellows Elected – 2019 (effective 1.1.2020) ....... 177 Foreign Fellows Elected – 2019 (effective 1.1.2020) ....... 181 Fellowship – Sectional Committeewise ....... 182 Local Chapters and Conveners ....... 215 COMMITTEES ....... 216 Standing Committees – 2020 ....... 217 Advisory Committees – 2020 ....... 221 Inter-Academy Panels ......