DOCSLIB.ORG

Chennai Mathematical Institute Annual Report 2009 - 2010 75 76 Chennai Mathematical Institute

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chennai Mathematical Institute Annual Report 2009 - 2010 75 76 Chennai Mathematical Institute Chennai Mathematical Institute Annual Report 2009 - 2010 H1, SIPCOT IT Park Padur Post, Siruseri, Tamilnadu 603 103. India. Chennai Mathematical Institute H1, SIPCOT IT Park Padur Post, Siruseri, Tamilnadu 603 103. India. Tel: +91-44-2747 0226 - 0229 +91-44-3298 3441 - 3442 Fax: +91-44-2747 0225 WWW: http://www.cmi.ac.in Design and Printing by: Balan Achchagam, Chennai 600 058 Contents 1. Preface ................................................................................................................... 5 2. Board of Trustees ................................................................................................. 9 3. Governing Council ............................................................................................. 10 4. Research Advisory Committee .......................................................................... 11 5. Academic Council ............................................................................................... 12 6. Boards of Studies ................................................................................................ 13 7. Institute Members ............................................................................................. 14 8. Faculty Profiles ................................................................................................... 17 9. Awards ................................................................................................................. 25 10. Research Activities ............................................................................................. 27 11. Publications ........................................................................................................ 33 12. The National Undergraduate Programme....................................................... 39 13. Activities of the Undergraduate Students....................................................... 43 14. Undergraduate/ Graduate Courses .................................................................. 45 15. Short Courses, Special Lectures ........................................................................ 47 16. Seminar Series for Summer Students in Mathematics .................................. 49 17. Special Semester on Analysis (January-April 2010) ....................................... 51 18. Advanced Training in Mathematics School .................................................... 53 19. Automata, Concurrency and Timed Systems (ACTS) II - February 2010 ...... 54 20. Conferences, Visits and External Lectures ...................................................... 57 21. Other Professional Activities ........................................................................... 65 22. Visitors ................................................................................................................ 69 23. Audited Statement of Accounts 2009-2010 .................................................... 74 Preface I take great pleasure in presenting the Annual Report of the Chennai Mathematical Institute for the period 2009-10. CMI continues to expand as a centre of excellence for research and teaching in the Mathematical Sciences. In addition to an active PhD programme that has been in place since the Institute was founded in 1989 , CMI has successfully run for over a decade a unique National Undergraduate Programme in Mathematics and Computer Science and in Physics, combined with a National Postgraduate Programme in Mathematics, Computer Science and, from this year, Applications of Mathematics. Several CMI graduates have completed PhDs at the best institutions across the world and are now well placed in academic and research positions in India and abroad. Alumni from CMI have also taken up corporate positions in areas such as software and finance. CMI has close academic cooperation with several institutions in India—special mention must be made of the Institute of Mathematical Sciences, Chennai—and abroad. Our collaboration with the Ecole Normale Supérieure of France continues with vigour with the three top students from BSc Mathematics and Computer Science going to Paris every summer for two months, while four students of the ENS come to CMI each year to teach in the undergraduate programme. CMI also sends its top three Physics graduates to the Ecole Polytechnique, France, for a summer internship. CMI has also signed an MoU with the Université Pierre et Marie Curie (Paris VI) for research collaboration. It also has similar MoUs with the Université de Paris-Sud, Orsay, France, and the ENS at Cachan, France. CMI is one of three non-European partners in the Erasmus Mundus Master Programme ALGANT (ALgebra Geometry And Number Theory), funded by the European Union. The ALGANT programme allows students to pursue Masters and Doctorate degrees across the institutions participating in the programme. Annual Report 2009 - 2010 5 We have had several academic programmes on campus this year. During May-July 2009, Dr Shrihari Sridharan coordinated a summer programme for students and research scholars, selected from universities and colleges. Some of the participants were sponsored by the Indian Academy of Sciences. The programme included regular lectures, lectures on special topics as well as project work mentored by faculty members. Nobel Laureate Prof Gerhard ’t Hooft visited CMI during November 2009. He gave five lectures, including a public lecture on “Mini Black Holes and Quantum Physics”. The celebrated astrophysicist Prof Jayant Narlikar visited CMI during February 2010 and gave a series of talks on the “Interaction between Astronomy, Physics and Mathematics” as well a public lecture on “Searches for Micro-life in Earth’s Atmosphere”. Both these visits were made possible by funding from the TCS-CMI Academic Alliance. Under the Advanced Training in Mathematics programme of the NBHM, an Annual Foundation School was coordinated by Dr Clare D’Cruz at CMI in December, 2009. CMI conducted two short courses in the series “Tools of the Mathematical Trade”. The first was by Prof Ramanan on “Spectral Sequences” in November, 2009 and the second on “Introduction to Intersection Theory and Motives” by Joel Riou of the University of Paris-Sud, Orsay, France in February, 2010. CMI also hosted two other short courses. Prof Michel Waldschmidt from the University of Paris 6, France delivered a course on “Modular Algebraic Independence” in December 2009 and January 2010. Prof Xavier Viennot from LaBRI, University of Bordeaux, France offered a course on “Algebraic Combinatorics” in January 2010. Professors Madhavan Mukund and K Narayan Kumar organized the 2nd Workshop on Automata, Concurrency and Timed Systems (ACTS II), during February 2010 at CMI with funding from TCS-CMI Academic Alliance and Ile-de-France/India project of the ARCUS programmme. Starting January 2010, CMI has been organising a special semester on Analysis. Several mathematicians, mainly from Indian Statistical Institute, Institute of Mathematical Sciences, Indian institute of science, TIFR have visited CMI and given lectures to students on various topics in analysis. This activity is being coordinated by Dr Shrihari Sridharan. 6 Chennai Mathematical Institute In addition to the generous support from the Department of Atomic Energy (DAE), CMI also receives support from private sources. I take this opportunity to thank the Shriram Group Companies, Bajaj Allianz and Agilent Technologies for their support. In April 2008, Chennai Mathematical Institute entered into a three year academic alliance with Tata Consultancy Services (TCS). Under this alliance, CMI faculty participate in training programmes at TCS and employees at TCS can enroll for the MSc Computer Science programme at CMI. TCS provides an annual grant to CMI that is used to fund computer equipment, academic visits to conferences and other institutions by CMI faculty and external visitors to CMI for academic collaboration. Academic visitors to CMI under this programme also deliver special lectures as part of the CMI-TCS Distinguished Lecture Series. I thank the DST and the Board for Research in Nuclear Sciences (BRNS) whose BRNS-DST grant has allowed us to have a vibrant visitors’ programme. The Ministry for Human Resources Development (MHRD) has used its good offices to organise a grant from the Universities Grants Commission (UGC) for an additional building to house an auditorium and additional academic space as well as guest rooms to accommodate visitors and students. CMI enjoys the goodwill of individual donors too. Dr. Swaminathan made a generous endowment in the memory of his uncle Mr. K. Lakshmanan and Mrs. Usha Rubugunday made a similar endowment in memory of her husband. This has led to annual Lakshmanan and Rubugunday memorial lectures at CMI. This year, Prof Kalyan Sinha delivered the “K. Lakshmanan Memorial Distinguished Lecture” and Prof Michel Waldschmidt delivered the “R.K. Rubugunday Distinguished Lecture”. As you can see by the instances cited above, CMI enjoys the support of public, academic and private institutions as well as students and private individuals. Thanks to this support, we have been able to establish CMI as a much desired destination to work in the mathematical sciences. I am sure that CMI will continue to grow as a centre of excellence in the years to come. C S SESHADRI Director Annual Report 2009 - 2010 7 8 Chennai Mathematical Institute Board of Trustees 1. Dr. A.C. Muthiah - Founder Trustee Chairman SPIC Ltd., Chennai 2. Shri N. Prasad - Trustee Chairman Matrix Laboratories, Hyderabad 3. Madhava
Load more

Recommended publications
  • Patent Filed, Commercialized & Granted Data
    Granted IPR Legends Applied IPR Total IPR filed till date 1995 S.No. Inventors Title IPA Date Grant Date 1 Prof. P K Bhattacharya (ChE) Process for the Recovery of 814/DEL/1995 03.05.1995 189310 05.05.2005 Inorganic Sodium Compounds from Kraft Black Liquor 1996 S.No. Inventors Title IPA Date Grant Date 1 Dr. Sudipta Mukherjee (ME), A Novel Attachment for Affixing to 1321/DEL/1996 12.08.1996 192495 28.10.2005 Anupam Nagory (Student, ME) Luggage Articles 2 Prof. Kunal Ghosh (AE) A Device for Extracting Power from 2673/DEL/1996 02.12.1996 212643 10.12.2007 to-and-fro Wind 1997 S.No. Inventors Title IPA Date Grant Date 1 Dr. D Manjunath, Jayesh V Shah Split-table Atm Multicast Switch 983/DEL/1997 17.04.1997 233357 29.03.2009 1998 S.No. Inventors Title IPA Date Grant Date 1999 1 Prof. K. A. Padmanabhan, Dr. Rajat Portable Computer Prinet 1521/DEL/1999 06.12.1999 212999 20.12.2007 Moona, Mr. Rohit Toshniwal, Mr. Bipul Parua 2000 S.No. Inventors Title IPA Date Grant Date 1 Prof. S. SundarManoharan (Chem), A Magnetic Polymer Composition 858/DEL/2000 22.09.2000 216744 24.03.2008 Manju Lata Rao and Process for the Preparation of the Same 2 Prof. S. Sundar Manoharan (Chem) Magnetic Cro2 – Polymer 933/DEL/2000 22.09.2000 217159 27.03.2008 Composite Blends 3 Prof. S. Sundar Manoharan (Chem) A Magneto Conductive Polymer 859/DEL/2000 22.09.2000 216743 19.03.2008 Compositon for Read and Write Head and a Process for Preparation Thereof 4 Prof.
    [Show full text]
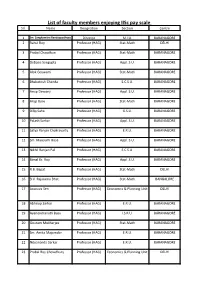
  • List of Faculty Members Enjoying Iisc Pay Scale Srl
    List of faculty members enjoying IISc pay scale Srl. Name Designation Section Centre 1 Sm. Sanghamitra Bandyopadhyay Director M.I.U. BARANAGORE 2 Rahul Roy Professor (HAG) Stat-Math DELHI 3 Probal Chaudhuri Professor (HAG) Stat-Math BARANAGORE 4 Debasis Sengupta Professor (HAG) Appl. S.U. BARANAGORE 5 Alok Goswami Professor (HAG) Stat-Math BARANAGORE 6 Bhabatosh Chanda Professor (HAG) E.C.S.U. BARANAGORE 7 Anup Dewanji Professor (HAG) Appl. S.U. BARANAGORE 8 Arup Bose Professor (HAG) Stat-Math BARANAGORE 9 Dilip Saha Professor (HAG) G.S.U. BARANAGORE 10 Palash Sarkar Professor (HAG) Appl. S.U. BARANAGORE 11 Satya Ranjan Chakravarty Professor (HAG) E.R.U. BARANAGORE 12 Sm. Mausumi Bose Professor (HAG) Appl. S.U. BARANAGORE 13 Nikhil Ranjan Pal Professor (HAG) E.C.S.U. BARANAGORE 14 Bimal Kr. Roy Professor (HAG) Appl. S.U. BARANAGORE 15 R.B. Bapat Professor (HAG) Stat-Math DELHI 16 B.V. Rajarama Bhat Professor (HAG) Stat-Math BANGALORE 17 Arunava Sen Professor (HAG) Economics & Planning Unit DELHI 18 Abhirup Sarkar Professor (HAG) E.R.U. BARANAGORE 19 Ayanendranath Basu Professor (HAG) I.S.R.U. BARANAGORE 20 Goutam Mukherjee Professor (HAG) Stat-Math BARANAGORE 21 Sm. Amita Majumder Professor (HAG) E.R.U. BARANAGORE 22 Nityananda Sarkar Professor (HAG) E.R.U. BARANAGORE 23 Prabal Roy Chowdhury Professor (HAG) Economics & Planning Unit DELHI 24 Subhamoy Maitra Professor (HAG) Appl. S.U. BARANAGORE 25 Tapas Samanta Professor (HAG) Appl. S.U. BARANAGORE 26 Abhay Gopal Bhatt Professor (HAG) Stat-Math DELHI 27 Atanu Biswas Professor (HAG) Appl. S.U.
    [Show full text]
  • Poly-Time Blackbox Identity Testing for Sum of Log-Variate Constant-Width Roabps
    Poly-time blackbox identity testing for sum of log-variate constant-width ROABPs Pranav Bisht ∗ Nitin Saxena † Abstract Blackbox polynomial identity testing (PIT) affords ‘extreme variable-bootstrapping’ (Agrawal et al, STOC’18; PNAS’19; Guo et al, FOCS’19). This motivates us to study log-variate read-once oblivious algebraic branching programs (ROABP). We restrict width of ROABP to a constant and study the more general sum-of-ROABPs model. We give the first poly(s)-time blackbox PIT for sum of constant-many, size-s, O(log s)-variate constant-width ROABPs. The previous best for this model was quasi-polynomial time (Gurjar et al, CCC’15; CC’16) which is comparable to brute-force in the log-variate setting. Also, we handle unbounded-many such ROABPs if each ROABP computes a homogeneous polynomial. Our new techniques comprise– (1) an ROABP computing a homogeneous polynomial can be made syntactically homogeneous in the same width; and (2) overcome the hurdle of unknown variable order in sum-of-ROABPs in the log-variate setting (over any field). 2012 ACM CCS concept: Theory of computation– Algebraic complexity theory, Fixed parameter tractability, Pseudorandomness and derandomization; Computing methodologies– Algebraic algorithms; Mathematics of computing– Combinatoric problems. Keywords: identity test, hitting-set, ROABP, blackbox, log variate, width, diagonal, derandom- ization, homogeneous, sparsity. 1 Introduction Polynomial Identity Testing (PIT) is the problem of testing whether a given multivariate polynomial is identically zero or not. The input polynomial to be tested is usually given in a compact representation– like an algebraic circuit or an algebraic branching program (ABP).
    [Show full text]
  • Indian Roots of Cryptography
    Algologic Technical Report # 2/2013 The Indian roots of cryptography S. Parthasarathy [email protected] Ref.: newcryptoroots.tex Ver. code: 20190123a Keywords : Alice, Bob, Sita, Rama, Vatsyayana, Kamasutra, Hemachan- dra, Fibonacci, Hindu, Arab, Numeral, Ramanujan, Agarwal, AKS, IITK Abstract This note is a sequel to my article [2] about the dramatis personae of cryptography. The article, provoked a world-wide reaction. In fact, a related Google search resulted in over 6 million hits, making me a kind of celebrity ! For those who care to be more reasonable and logical, here is some more evidence to strengthen the proposal I made earlier in my article about Sita and Rama. 1 The Indian roots of cryptography The article [2] about Alice and Bob, talks about the dramatis personae of cryptography, and proposes a much more meaningful alternative. The au- thor came across many situations when contributions by India are unfairly understated or ignored completely by the cryptography community. We take a quick look at some of them. One remarkable exception is the book by Kim Plofker [15], a well-documented book which is free of bias and exaggeration. Most books on cryptography invariably include the Caesar’s cipher as an example of substitution cipher. It is strange that they all ignore, or are unaware of another substitution cipher which was in use a few centuries before Caesar’s cipher. According to [1] Cryptography is recommended in the Kama Sutra (ca 400 BCE) as a way for lovers to communicate without inconvenient discovery. 1 The Signal Corps Association [3], gives an interesting explanation of the kama sutra cipher.
    [Show full text]
  • Lipics-CCC-2021-11.Pdf (1
    Deterministic Identity Testing Paradigms for Bounded Top-Fanin Depth-4 Circuits Pranjal Dutta # Ñ Chennai Mathematical Institute, India Department of Computer Science & Engineering, IIT Kanpur, India Prateek Dwivedi # Ñ Department of Computer Science & Engineering, IIT Kanpur, India Nitin Saxena # Ñ Department of Computer Science & Engineering, IIT Kanpur, India Abstract Polynomial Identity Testing (PIT) is a fundamental computational problem. The famous depth-4 reduction (Agrawal & Vinay, FOCS’08) has made PIT for depth-4 circuits, an enticing pursuit. The largely open special-cases of sum-product-of-sum-of-univariates (Σ[k]ΠΣ∧) and sum-product- of-constant-degree-polynomials (Σ[k]ΠΣΠ[δ]), for constants k, δ, have been a source of many great ideas in the last two decades. For eg. depth-3 ideas (Dvir & Shpilka, STOC’05; Kayal & Saxena, CCC’06; Saxena & Seshadhri, FOCS’10, STOC’11); depth-4 ideas (Beecken,Mittmann & Saxena, ICALP’11; Saha,Saxena & Saptharishi, Comput.Compl.’13; Forbes, FOCS’15; Kumar & Saraf, CCC’16); geometric Sylvester-Gallai ideas (Kayal & Saraf, FOCS’09; Shpilka, STOC’19; Peleg & Shpilka, CCC’20, STOC’21). We solve two of the basic underlying open problems in this work. We give the first polynomial-time PIT for Σ[k]ΠΣ∧. Further, we give the first quasipolynomial time blackbox PIT for both Σ[k]ΠΣ∧ and Σ[k]ΠΣΠ[δ]. No subexponential time algorithm was known prior to this work (even if k = δ = 3). A key technical ingredient in all the three algorithms is how the logarithmic derivative, and its power-series, modify the top Π-gate to ∧. 2012 ACM Subject Classification Theory of computation → Algebraic complexity theory Keywords and phrases Polynomial identity testing, hitting set, depth-4 circuits Digital Object Identifier 10.4230/LIPIcs.CCC.2021.11 Funding Pranjal Dutta: Google Ph.
    [Show full text]
  • Classifying Polynomials and Identity Testing
    Classifying polynomials and identity testing MANINDRA AGRAWAL1,∗ and RAMPRASAD SAPTHARISHI2 1Indian Institute of Technology, Kanpur, India. 2Chennai Mathematical Institute, and Indian Institute of Technology, Kanpur, India. e-mail: [email protected] One of the fundamental problems of computational algebra is to classify polynomials according to the hardness of computing them. Recently, this problem has been related to another important problem: Polynomial identity testing. Informally, the problem is to decide if a certain succinct representation of a polynomial is zero or not. This problem has been extensively studied owing to its connections with various areas in theoretical computer science. Several efficient randomized algorithms have been proposed for the identity testing problem over the last few decades but an efficient deterministic algorithm is yet to be discovered. It is known that such an algorithm will imply hardness of computing an explicit polynomial. In the last few years, progress has been made in designing deterministic algorithms for restricted circuits, and also in understanding why the problem is hard even for small depth. In this article, we survey important results for the polynomial identity testing problem and its connection with classification of polynomials. 1. Introduction its simplicity. For example, consider the polyno- mials The interplay between mathematics and computer ··· science demands algorithmic approaches to vari- (1 + x1)(1 + x2) (1 + xn) ous algebraic constructions. The area of computa- and tional algebra addresses precisely this. The most fundamental objects in algebra are polynomials x1x2 ···xn. and it is a natural idea to classify the polyno- mials according to their ‘simplicity’. The algorith- The former has 2n − 1 more terms than the later, mic approach suggests that the simple polynomials however, both are almost equally easy to describe are those that can be computed easily.
    [Show full text]
  • Honours Number Theory : the Agrawal-Kayal-Saxena Primality Test
    MATH 377 - Honours Number Theory : The Agrawal-Kayal-Saxena Primality Test Azeem Hussain May 4, 2013 1 Introduction Whether or not a number is prime is one of its most fundamental properties. Many branches of pure mathematics rely heavily on numbers being prime. Prime numbers are in some sense the purest. Irreducible (over Z), they are the building blocks of all other numbers. And yet, determining if a number is prime is not an easy task, certainly not if the number is very large. There are various algorithms for primality testing. For example, the Sieve of Eratos- thenes, developed in Ancient Greece. Reliable, it works on all inputs. The problem is that it takes very long. The running time is exponential in the size of the input. Miller devised a test for primality that runs in polynomial time [1]. The problem is that is assumes the extended Riemann hypothesis. Rabin adapted Miller’s test to yield a reliable polynomial time primality test, the Miller- Rabin test [2]. This test works well in practice. The problem is that the test is randomized and not guaranteed to work. However, the probability or error can be made miniscule by successive repetition. Nevertheless, to the mathematician, this leaves something to be desired. Ideally, the test will produce a certificate, a proof that the number is prime. This test can only say that the number is “probably prime.” Most primality tests fall into one of these three categories. Either they scale exponen- tially in time with the input, they rely on some conjecture, or they are randomized.
    [Show full text]
  • Infosys Prize 2017
    Infosys Science Foundation INFOSYS PRIZE 2017 The Romanesco broccoli has fascinated photographers the world over. The brilliant chartreuse and the mesmerizing spiral spines belong to an edible flower bud of the species Brassica oleracea. Grown in Italy since the 16th century, this broccoli- cauliflower hybrid is nutritionally rich, with a delicate nutty flavor. Romanesco thus demands as much interest from chefs as from botanists and researchers. But it doesn’t stop there – peer closely and you will see just how incredible it really is. For it is one of the earth’s most stunning natural fractals. In other words, each of its buds is composed of a series of smaller buds, all arranged in yet another logarithmic spiral. The same pattern continues at several diminishing size levels. Studies of fractals found in nature, such as a snowflake or lightning bolts or indeed the Romanesco broccoli, trace a path to modern applications in computer graphics. We tend to divide and study distinct subjects – physics, biology, math, engineering and so on – only to find one interconnected universe. And it gets even more bizarre. The number of spirals on the head of a Romanesco broccoli is a natural approximation of the Fibonacci number. Named after the Italian mathematician, the Fibonacci spiral is a logarithmic spiral where every quarter turn is farther from the origin by a factor of phi, the golden ratio. How about that for a little bit of math in your soup? ENGINEERING AND COMPUTER SCIENCE The Infosys Prize 2017 in Engineering and Computer Science is awarded to Prof. Sanghamitra Bandyopadhyay for her scholarly record in algorithmic optimization and for its significant impact on biological data analysis.
    [Show full text]
  • What Does It Mean That PRIMES Is in P? Popularization and Distortion Revisited
    - 1 - What does It Mean that PRIMES is in P? Popularization and Distortion Revisited Boaz Miller This paper was published with very minor changes in Social Studies of Science 39:2, 2009, pp. 257-288. Abstract In August 2002, three Indian computer scientists published a paper, ‘PRIMES is in P’, online. It presents a ‘deterministic algorithm’ which determines in ‘polynomial time’ if a given number is a prime number. The story was quickly picked up by the general press, and by this means spread through the scientific community of complexity theorists, where it was hailed as a major theoretical breakthrough. This is although scientists regarded the media reports as vulgar popularizations. When the paper was published in a peer-reviewed journal only two years later, the three scientists had already received wide recognition for their accomplishment. Current sociological theory challenges the ability to clearly distinguish on independent epistemic grounds between distorted and non-distorted scientific knowledge. It views the demarcation lines between such forms of presentation as contextual and unstable. In my paper, I challenge this view. By systematically surveying the popular press coverage of the ‘PRIMES is in P’ affair, I argue-- against the prevailing new orthodoxy--that distorted simplifications of scientific knowledge are distinguishable from non-distorted simplifications on independent epistemic grounds. I argue that in the ‘PRIMES is in P’ affair, the three scientists could ride on the wave of the general press-distorted coverage of their algorithm, while counting on their colleagues’ ability to distinguish genuine accounts from distorted ones. Thus, their scientific reputation was unharmed.
    [Show full text]
  • CV (Nitin Saxena)
    CV (Nitin Saxena) Personal Information Name: NITIN SAXENA Address: RM203, Department of CSE, IIT Kanpur, Kanpur-208016 ; +91-512-679-7588 E-address: [email protected] ; https://www.cse.iitk.ac.in/users/nitin/ Date and place of birth: 3rd MAY 1981, Allahabad/Prayagraj, India Nationality: INDIA Gender: M S Degree Subject Year University Additional No Particulars 1 B.Tech. Computer 2002 Indian Institute of Thesis: Towards a Science & Technology deterministic polynomial- Engineering, Kanpur time primality test (Won Algebra, the best BTech CSE Number theory Project Award 2002) 2 Ph.D. Computer 2006 Indian Institute of Thesis: Morphisms of Science & Technology Rings and Applications to Engineering, Kanpur Complexity (Won Algebra, Outstanding PhD Student Number theory Award of IBM India Research Lab 2005) Guide: Manindra Agrawal 3 Post-Doc Mathematics, 2006- CWI (Centrum Host: Prof.dr.Harry Research Informatics, 08 voor Wiskunde en Buhrman Quantum Informatica) complexity Amsterdam, Netherlands Date of joining the Institution (Designation & Scale): 05-Nov-2018, Professor (CSE), AcadLevel=14A, Basic=173900/- Positions held earlier (in chronological order): S Period Place of Employment Designation No 1 Jul'02- CSE, IIT Kanpur Infosys PhDFellow Jul'06 2 Sep'03- CS, Princeton University, USA Visiting Student Research Aug'04 Collaborator 3 Sep'04- CS, National University of Singapore Visiting Scholar Jun'05 4 Sep'06- CWI Amsterdam, The Netherlands Scientific Researcher Mar'08 5 Apr'08- Hausdorff Center for Mathematics, Professor W2, Mar'13 University of Bonn, Germany BonnJuniorFellow 6 Dec'14 UPMC Paris-6, France Visiting Professor 7 Aug'18- Chennai Mathematical Institute, H1, Adjunct Professor Jul'21 SIPCOT IT Park, Chennai.
    [Show full text]
  • A Celebration of Mathematics 2018 Ramanujan Prize Award
    SRINIVASA RAMANUJAN A CELEBRATION OF MATHEMATICS Srinivasa Ramanujan was born in 1887 in Erode, Tamil Nadu, India. He grew up in poverty and hardship. Ramanujan was unable to pass his school examinations, and could only obtain a clerk’s position in the city of Madras. 2018 RAMANUJAN PRIZE However, he was a genius in pure mathematics and essentially self-taught from a single text book that was available to him. He continued to pursue AWARD CEREMONY his own mathematics, and sent letters to three mathematicians in England, containing some of his results. While two of the three returned the letters unopened, G.H. Hardy recognized Ramanujan’s intrinsic mathematical ability and arranged for him to go to Cambridge. Hardy was thus responsible for ICTP making Ramanujan’s work known to the world during the latter’s own lifetime. Ramanujan made spectacular contributions to elliptic functions, continued 9 November 2018 fractions, infinite series, and analytical theory of numbers. His health deteriorated rapidly while in England. He was sent home to recuperate in 1919, but died the next year at the age of 32. RAMANUJAN PRIZE In 2005 the Abdus Salam International Centre for Theoretical Physics (ICTP) established the Srinivasa Ramanujan Prize for Young Mathematicians from Developing Countries, named after the mathematics genius from India. This Prize is awarded annually to a mathematician under 45. Since the mandate of ICTP is to strengthen science in developing countries, the Ramanujan Prize has been created for mathematicians from developing countries. Since Ramanujan is the quintessential symbol of the best in mathematics from the developing world, naming the Prize after him seemed entirely appropriate.
    [Show full text]
  • B3-I School of Mathematics (Math)
    B3-I School of Mathematics (Math) Evaluative Report of Departments (B3) I-Math-1 School of Mathematics 1. Name of the Department : School of Mathematics (Math) 2. Year of establishment : 1945 3. Is the Department part of a School/Faculty of the university? It is an entire School. 4. Names of programmes offered (UG, PG, M.Phil., Ph.D., Integrated Masters; Integrated Ph.D., D. Sc, D. Litt, etc.) 1. Ph.D. 2. Integrated M.Sc.-Ph.D. The minimum eligibility criterion for admission to the Ph.D. programme is a Master's degree in any of Mathematics/Statistics/Science/Technology (M.A. / M.Sc. / M. Math / M. Stat / M.E. / M. Tech.). The minimum eligibility criterion for admission to the Integrated Ph.D. programme is a Bachelor's degree in any of Mathematics/Statistics/Science/Technology (B.A. / B.Sc. / B. Math. / B. Stat. / B.E. / B. Tech.). Students without a Master's degree will generally be admitted to the Integrated Ph.D. program and will obtain an M.Sc. degree along the way subject to the completion of all requirements. Students with a four-year Bachelor's degree may be considered for admission to the Ph.D. Programme. 5. Interdisciplinary programmes and departments involved None 6. Courses in collaboration with other universities, industries, foreign institutions, etc. None TIFR NAAC Self-Study Report 2016 I-Math-2 Evaluative Report of Departments (B3) 7. Details of programmes discontinued, if any, with reasons There are no such programmes. 8. Examination System: Annual/Semester/Trimester/Choice Based Credit System There is an evaluation at the end of each semester course, based on assignments and written examinations, and an annual evaluation of courses based on an interview.
    [Show full text]