A Celebration of Mathematics 2018 Ramanujan Prize Award
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Notices of the American Mathematical Society June/July 2006
of the American Mathematical Society ... (I) , Ate._~ f.!.o~~Gffi·u. .4-e.e..~ ~~~- •i :/?I:(; $~/9/3, Honoring J ~ rt)d ~cLra-4/,:e~ o-n. /'~7 ~ ~<A at a Gift from fL ~ /i: $~ "'7/<J/3. .} -<.<>-a.-<> ~e.Lz?-1~ CL n.y.L;; ro'T>< 0 -<>-<~:4z_ I Kumbakonam li .d. ~ ~~d a. v#a.d--??">ovt<.·c.-6 ~~/f. t:JU- Lo,.,do-,......) ~a page 640 ~!! ?7?.-L ..(; ~7 Ca.-uM /3~~-d~ .Y~~:Li: ~·e.-l a:.--nd '?1.-d- p ~ .di.,r--·c/~ C(c£~r~~u . J~~~aq_ f< -e-.-.ol ~ ~ ~/IX~ ~ /~~ 4)r!'a.. /:~~c~ •.7~ The Millennium Grand Challenge .(/.) a..Lu.O<"'? ...0..0~ e--ne_.o.AA/T..C<.r~- /;;; '7?'E.G .£.rA-CLL~ ~ ·d ~ in Mathematics C>n.A..U-a.A-d ~~. J /"-L .h. ?n.~ ~?(!.,£ ~ ~ &..ct~ /U~ page 652 -~~r a-u..~~r/a.......<>l/.k> 0?-t- ~at o ~~ &~ -~·e.JL d ~~ o(!'/UJD/ J;I'J~~Lcr~~ 0 ??u£~ ifJ>JC.Qol J ~ ~ ~ -0-H·d~-<.() d Ld.orn.J,k, -F-'1-. ~- a-o a.rd· J-c~.<-r:~ rn-u-{-r·~ ~'rrx ~~/ ~-?naae ~~ a...-'XS.otA----o-n.<l C</.J.d:i. ~~~ ~cL.va- 7 ??.L<A) ~ - Ja/d ~~ ./1---J- d-.. ~if~ ~0:- ~oj'~ t1fd~u: - l + ~ _,. :~ _,. .~., -~- .. =- ~ ~ d.u. 7 ~'d . H J&."dIJ';;;::. cL. r ~·.d a..L- 0.-n(U. jz-o-cn-...l- o~- 4; ~ .«:... ~....£.~.:: a/.l~!T cLc.·£o.-4- ~ d.v. /-)-c~ a;- ~'>'T/JH'..,...~ ~ d~~ ~u ~ ~ a..t-4. l& foLk~ '{j ~~- e4 -7'~ -£T JZ~~c~ d.,_ .&~ o-n ~ -d YjtA:o ·C.LU~ ~or /)-<..,.,r &-. -

Indian Mathematics
Indian Mathemtics V. S. Varadarajan University of California, Los Angeles, CA, USA UCLA, March 3-5, 2008 Abstract In these two lectures I shall talk about some Indian mathe- maticians and their work. I have chosen two examples: one from the 7th century, Brahmagupta, and the other, Ra- manujan, from the 20th century. Both of these are very fascinating figures, and their histories illustrate various as- pects of mathematics in ancient and modern times. In a very real sense their works are still relevant to the mathe- matics of today. Some great ancient Indian figures of Science Varahamihira (505–587) Brahmagupta (598-670) Bhaskara II (1114–1185) The modern era Ramanujan, S (1887–1920) Raman, C. V (1888–1970) Mahalanobis, P. C (1893–1972) Harish-Chandra (1923–1983) Bhaskara represents the peak of mathematical and astro- nomical knowledge in the 12th century. He reached an un- derstanding of calculus, astronomy, the number systems, and solving equations, which were not to be achieved any- where else in the world for several centuries...(Wikipedia). Indian science languished after that, the British colonial occupation did not help, but in the 19th century there was a renaissance of arts and sciences, and Indian Science even- tually reached a level comparable to western science. BRAHMAGUPTA (598–670c) Some quotations of Brahmagupta As the sun eclipses the stars by its brilliancy, so the man of knowledge will eclipse the fame of others in assemblies of the people if he proposes algebraic problems, and still more, if he solves them. Quoted in F Cajori, A History of Mathematics A person who can, within a year, solve x2 92y2 =1, is a mathematician. -
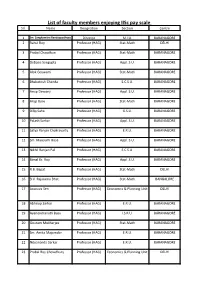
List of Faculty Members Enjoying Iisc Pay Scale Srl
List of faculty members enjoying IISc pay scale Srl. Name Designation Section Centre 1 Sm. Sanghamitra Bandyopadhyay Director M.I.U. BARANAGORE 2 Rahul Roy Professor (HAG) Stat-Math DELHI 3 Probal Chaudhuri Professor (HAG) Stat-Math BARANAGORE 4 Debasis Sengupta Professor (HAG) Appl. S.U. BARANAGORE 5 Alok Goswami Professor (HAG) Stat-Math BARANAGORE 6 Bhabatosh Chanda Professor (HAG) E.C.S.U. BARANAGORE 7 Anup Dewanji Professor (HAG) Appl. S.U. BARANAGORE 8 Arup Bose Professor (HAG) Stat-Math BARANAGORE 9 Dilip Saha Professor (HAG) G.S.U. BARANAGORE 10 Palash Sarkar Professor (HAG) Appl. S.U. BARANAGORE 11 Satya Ranjan Chakravarty Professor (HAG) E.R.U. BARANAGORE 12 Sm. Mausumi Bose Professor (HAG) Appl. S.U. BARANAGORE 13 Nikhil Ranjan Pal Professor (HAG) E.C.S.U. BARANAGORE 14 Bimal Kr. Roy Professor (HAG) Appl. S.U. BARANAGORE 15 R.B. Bapat Professor (HAG) Stat-Math DELHI 16 B.V. Rajarama Bhat Professor (HAG) Stat-Math BANGALORE 17 Arunava Sen Professor (HAG) Economics & Planning Unit DELHI 18 Abhirup Sarkar Professor (HAG) E.R.U. BARANAGORE 19 Ayanendranath Basu Professor (HAG) I.S.R.U. BARANAGORE 20 Goutam Mukherjee Professor (HAG) Stat-Math BARANAGORE 21 Sm. Amita Majumder Professor (HAG) E.R.U. BARANAGORE 22 Nityananda Sarkar Professor (HAG) E.R.U. BARANAGORE 23 Prabal Roy Chowdhury Professor (HAG) Economics & Planning Unit DELHI 24 Subhamoy Maitra Professor (HAG) Appl. S.U. BARANAGORE 25 Tapas Samanta Professor (HAG) Appl. S.U. BARANAGORE 26 Abhay Gopal Bhatt Professor (HAG) Stat-Math DELHI 27 Atanu Biswas Professor (HAG) Appl. S.U. -

After Ramanujan Left Us– a Stock-Taking Exercise S
Ref: after-ramanujanls.tex Ver. Ref.: : 20200426a After Ramanujan left us– a stock-taking exercise S. Parthasarathy [email protected] 1 Remembering a giant This article is a sequel to my article on Ramanujan [14]. April 2020 will mark the death centenary of the legendary Indian mathe- matician – Srinivasa Ramanujan (22 December 1887 – 26 April 1920). There will be celebrations of course, but one way to honour Ramanujan would be to do some introspection and stock-taking. This is a short survey of notable achievements and contributions to mathematics by Indian institutions and by Indian mathematicians (born in India) and in the last hundred years since Ramanujan left us. It would be highly unfair to compare the achievements of an individual, Ramanujan, during his short life span (32 years), with the achievements of an entire nation over a century. We should also consider the context in which Ramanujan lived, and the most unfavourable and discouraging situation in which he grew up. We will still attempt a stock-taking, to record how far we have moved after Ramanujan left us. Note : The table below should not be used to compare the relative impor- tance or significance of the contributions listed there. It is impossible to list out the entire galaxy of mathematicians for a whole century. The table below may seem incomplete and may contain some inad- vertant errors. If you notice any major lacunae or omissions, or if you have any suggestions, please let me know at [email protected]. 1 April 1920 – April 2020 Year Name/instit. Topic Recognition 1 1949 Dattatreya Kaprekar constant, Ramchandra Kaprekar number Kaprekar [1] [2] 2 1968 P.C. -

Srinivasa Ramanujan Iyengar
Srinivasa Ramanujan Iyengar Srinivasa Ramanujan Iyengar (Srinivāsa Rāmānujan Iyengār)() (December 22, 1887 – April 26, 1920) was an Indian mathematician widely regarded as one of the greatest mathematical minds in recent history. With almost no formal training in mathematics, he made profound contributions in the areas of analysis and number theory. A child prodigy, Ramanujan was largely self-taught and compiled nearly 3,884 theorems during his short lifetime. Although a small number of these theorems were actually false, most of his statements have now been proven to be correct. His deep intuition and uncanny algebraic manipulative ability enabled him to state highly original and unconventional results that have inspired a vast amount of research; however, some of his discoveries have been slow to enter the mathematical mainstream. Recently his formulae have begun to be applied in the field of crystallography and physics. The Ramanujan Journal was launched specifically to publish work "in areas of mathematics influenced by Ramanujan". With the encouragement of friends, he wrote to mathematicians in Cambridge seeking validation of his work. Twice he wrote with no response; on the third try, he found the English Mathematician G. H. Hardy. Ramanujan's arrival at Cambridge (March 1914) was the beginning of a very successful five-year collaboration with Hardy. One remarkable result of the Hardy-Ramanujan collaboration was a formula for the number p(n) exp(π 2n /3) of partitions of a number n: pn()∼ asn→∞.A partition of a positive integer n is just an expression for n as a sum of 43n positive integers, regardless of order. -

Secondary Indian Culture and Heritage
Culture: An Introduction MODULE - I Understanding Culture Notes 1 CULTURE: AN INTRODUCTION he English word ‘Culture’ is derived from the Latin term ‘cult or cultus’ meaning tilling, or cultivating or refining and worship. In sum it means cultivating and refining Ta thing to such an extent that its end product evokes our admiration and respect. This is practically the same as ‘Sanskriti’ of the Sanskrit language. The term ‘Sanskriti’ has been derived from the root ‘Kri (to do) of Sanskrit language. Three words came from this root ‘Kri; prakriti’ (basic matter or condition), ‘Sanskriti’ (refined matter or condition) and ‘vikriti’ (modified or decayed matter or condition) when ‘prakriti’ or a raw material is refined it becomes ‘Sanskriti’ and when broken or damaged it becomes ‘vikriti’. OBJECTIVES After studying this lesson you will be able to: understand the concept and meaning of culture; establish the relationship between culture and civilization; Establish the link between culture and heritage; discuss the role and impact of culture in human life. 1.1 CONCEPT OF CULTURE Culture is a way of life. The food you eat, the clothes you wear, the language you speak in and the God you worship all are aspects of culture. In very simple terms, we can say that culture is the embodiment of the way in which we think and do things. It is also the things Indian Culture and Heritage Secondary Course 1 MODULE - I Culture: An Introduction Understanding Culture that we have inherited as members of society. All the achievements of human beings as members of social groups can be called culture. -

Profile Book 2017
MATH MEMBERS A. Raghuram Debargha Banerjee Neeraj Deshmukh Sneha Jondhale Abhinav Sahani Debarun Ghosh Neha Malik Soumen Maity Advait Phanse Deeksha Adil Neha Prabhu Souptik Chakraborty Ajith Nair Diganta Borah Omkar Manjarekar Steven Spallone Aman Jhinga Dileep Alla Onkar Kale Subham De Amit Hogadi Dilpreet Papia Bera Sudipa Mondal Anindya Goswami Garima Agarwal Prabhat Kushwaha Supriya Pisolkar Anisa Chorwadwala Girish Kulkarni Pralhad Shinde Surajprakash Yadav Anup Biswas Gunja Sachdeva Rabeya Basu Sushil Bhunia Anupam Kumar Singh Jyotirmoy Ganguly Rama Mishra Suvarna Gharat Ayan Mahalanobis Kalpesh Pednekar Ramya Nair Tathagata Mandal Ayesha Fatima Kaneenika Sinha Ratna Pal Tejas Kalelkar Baskar Balasubramanyam Kartik Roy Rijubrata Kundu Tian An Wong Basudev Pattanayak Krishna Kaipa Rohit Holkar Uday Bhaskar Sharma Chaitanya Ambi Krishna Kishore Rohit Joshi Uday Jagadale Chandrasheel Bhagwat Makarand Sarnobat Shane D'Mello Uttara Naik-Nimbalkar Chitrabhanu Chaudhuri Manidipa Pal Shashikant Ghanwat Varun Prasad Chris John Manish Mishra Shipra Kumar Venkata Krishna Debangana Mukherjee Milan Kumar Das Shuvamkant Tripathi Visakh Narayanan Debaprasanna Kar Mousomi Bhakta Sidharth Vivek Mohan Mallick Compiling, Editing and Design: Shanti Kalipatnapu, Kranthi Thiyyagura, Chandrasheel Bhagwat, Anisa Chorwadwala Art on the Cover: Sinjini Bhattacharjee, Arghya Rakshit Photo Courtesy: IISER Pune Math Members 2017 IISER Pune Math Book WELCOME MESSAGE BY COORDINATOR I have now completed over five years at IISER Pune, and am now in my sixth and possibly final year as Coordinator for Mathematics. I am going to resist the temptation of evaluating myself as to what I have or have not accomplished as head of mathematics, although I do believe that it’s always fruitful to take stock, to become aware of one’s strengths, and perhaps even more so of one’s weaknesses, especially when the goal we have set for ourselves is to become a strong force in the international world of Mathematics. -

Scheme of Instruction 2021 - 2022
Scheme of Instruction Academic Year 2021-22 Part-A (August Semester) 1 Index Department Course Prefix Page No Preface : SCC Chair 4 Division of Biological Sciences Preface 6 Biological Science DB 8 Biochemistry BC 9 Ecological Sciences EC 11 Neuroscience NS 13 Microbiology and Cell Biology MC 15 Molecular Biophysics Unit MB 18 Molecular Reproduction Development and Genetics RD 20 Division of Chemical Sciences Preface 21 Chemical Science CD 23 Inorganic and Physical Chemistry IP 26 Materials Research Centre MR 28 Organic Chemistry OC 29 Solid State and Structural Chemistry SS 31 Division of Physical and Mathematical Sciences Preface 33 High Energy Physics HE 34 Instrumentation and Applied Physics IN 38 Mathematics MA 40 Physics PH 49 Division of Electrical, Electronics and Computer Sciences (EECS) Preface 59 Computer Science and Automation E0, E1 60 Electrical Communication Engineering CN,E1,E2,E3,E8,E9,MV 68 Electrical Engineering E0,E1,E4,E5,E6,E8,E9 78 Electronic Systems Engineering E0,E2,E3,E9 86 Division of Mechanical Sciences Preface 95 Aerospace Engineering AE 96 Atmospheric and Oceanic Sciences AS 101 Civil Engineering CE 104 Chemical Engineering CH 112 Mechanical Engineering ME 116 Materials Engineering MT 122 Product Design and Manufacturing MN, PD 127 Sustainable Technologies ST 133 Earth Sciences ES 136 Division of Interdisciplinary Research Preface 139 Biosystems Science and Engineering BE 140 Scheme of Instruction 2021 - 2022 2 Energy Research ER 144 Computational and Data Sciences DS 145 Nanoscience and Engineering NE 150 Management Studies MG 155 Cyber Physical Systems CP 160 Scheme of Instruction 2020 - 2021 3 Preface The Scheme of Instruction (SoI) and Student Information Handbook (Handbook) contain the courses and rules and regulations related to student life in the Indian Institute of Science. -

IISER AR PART I A.Cdr
dm{f©H$ à{VdoXZ Annual Report 2016-17 ^maVr¶ {dkmZ {ejm Ed§ AZwg§YmZ g§ñWmZ nwUo Indian Institute of Science Education and Research Pune XyaX{e©Vm Ed§ bú` uCƒV‘ j‘Vm Ho$ EH$ Eogo d¡km{ZH$ g§ñWmZ H$s ñWmnZm {Og‘| AË`mYw{ZH$ AZwg§YmZ g{hV AÜ`mnZ Ed§ {ejm nyU©ê$n go EH$sH¥$V hmo& u{Okmgm Am¡a aMZmË‘H$Vm go `wº$ CËH¥$ï> g‘mH$bZmË‘H$ AÜ`mnZ Ho$ ‘mÜ`m‘ go ‘m¡{bH$ {dkmZ Ho$ AÜ``Z H$mo amoMH$ ~ZmZm& ubMrbo Ed§ Agr‘ nmR>çH«$‘ VWm AZwg§YmZ n[a`moOZmAm| Ho$ ‘mÜ`‘ go N>moQ>r Am`w ‘| hr AZwg§YmZ joÌ ‘| àdoe& Vision & Mission uEstablish scientific institution of the highest caliber where teaching and education are totally integrated with state-of-the-art research uMake learning of basic sciences exciting through excellent integrative teaching driven by curiosity and creativity uEntry into research at an early age through a flexible borderless curriculum and research projects Annual Report 2016-17 Correct Citation IISER Pune Annual Report 2016-17, Pune, India Published by Dr. K.N. Ganesh Director Indian Institute of Science Education and Research Pune Dr. Homi J. Bhabha Road Pashan, Pune 411 008, India Telephone: +91 20 2590 8001 Fax: +91 20 2025 1566 Website: www.iiserpune.ac.in Compiled and Edited by Dr. Shanti Kalipatnapu Dr. V.S. Rao Ms. Kranthi Thiyyagura Photo Courtesy IISER Pune Students and Staff © No part of this publication be reproduced without permission from the Director, IISER Pune at the above address Printed by United Multicolour Printers Pvt. -

Muramatsu's Method Aryabhata (499 AD) Brahmagupta (640 AD
π in Other Eastern Countries Japan India In the Edo Period of Japan (1603 to 1868), 3.16 was used for π. But Aryabhata (499 AD) as people recognized that this value was not accurate, different values for π were calculated. Wasan scholars such as Muramatsu Shigekiyo, Seki Takakazu, Kamata Toshikiyo, Takebe Katahiro, and Matsunaga Aryabhata usedp the perimeter of a 384-sided poly- Yoshisuke all made calculations of π, and accomplished results gon to find π ≈ 9:8684. Later Aryabhata would comparable to their European mathematician counterparts. publish an “approximation” for his square root value, 3.1416. Note that his approximation is Muramatsu’s Method more accurate than his official value! Shigekiyo Muramatsu published Sanso in 1663. Muramatsu served the Asano family and possibly had a math insti- Brahmagupta (640 AD) tute in Edo (present day Tokyo). In his Brahmagupta used a pattern of inscribed polygons that work, Sanso, Muramatsu arranged prob- increased in the number of sides to calculate the perime- lems published earlier in Japanese math- ter of a circle.p Using these data points, he came to believe ematics texts without answers. Mura- that π = 10: matsu classified these problems into dif- ferent levels according to how difficult he thought they’d be to learn. Asano Crest It is in this book that he also showed the calculation of π from the regular inscribed polygon of 32,768 sides. He correctly obtained the Ramanujan (1887-1920) value 3.1415926. Thus, this book was the first to contain a mathematical calculation of π in Japan. 1 Srinivasa Ramanujan found several formulas for π. -

Ancient India and Mathematics Sundar Sarukkai
11 Ancient India and Mathematics Sundar Sarukkai ne way to approach this very broad topic is to list There are some things in all that the ancient Indian mathematicians did – common between Indian and Oand they did do an enormous amount of Greek Mathematics but there Mathematics: arithmetic (including the creation of decimal are also significant differences – place notation, the invention of zero), trigonometry (the not just in style but also in the detailed tables of sines), algebra (binomial theorem, larger world view (which influences, for solving quadratic equations), astronomy and astrology example, the completely different ways of understanding (detailed numerical calculations). Later Indian the nature of numbers in the Greek and the Indian Mathematics, the Kerala school, discovered the notions of traditions). This difference has led many writers to claim infinite series, limits and analysis which are the precursors that Indians (and Chinese among others) did not possess to calculus. the notions of Science and Mathematics. The first, and enduring response, to the question of Science and Since these details are easily available I am not going to list Mathematics in ancient non-Western civilizations is one of them here. What is of interest to me is to understand in skepticism. Did the Indians and Chinese really have Science what sense these activities were 'mathematical'. By doing and Mathematics as we call it now? This skepticism has so, I am also responding to the charge that these people been held over centuries and by the most prominent were not doing Mathematics but something else. This is a thinkers of the west (and is in fact so widespread as to charge similar to that addressed to Science in ancient India include claims that Indians did not 'have' philosophy, logic – the claim here is that what was being done in metallurgy, and even religion). -

Profiles and Prospects*
Indian Journal of History of Science, 47.3 (2012) 473-512 MATHEMATICS AND MATHEMATICAL RESEARCHES IN INDIA DURING FIFTH TO TWENTIETH CENTURIES — PROFILES AND PROSPECTS* A K BAG** (Received 1 September 2012) The Birth Centenary Celebration of Professor M. C. Chaki (1912- 2007), former First Asutosh Birth Centenary Professor of Higher Mathematics and a noted figure in the community of modern geometers, took place recently on 21 July 2012 in Kolkata. The year 2012 is also the 125th Birth Anniversary Year of great mathematical prodigy, Srinivas Ramanujan (1887-1920), and the Government of India has declared 2012 as the Year of Mathematics. To mark the occasion, Dr. A. K. Bag, FASc., one of the students of Professor Chaki was invited to deliver the Key Note Address. The present document made the basis of his address. Key words: Algebra, Analysis, Binomial expansion, Calculus, Differential equation, Fluid and solid mechanics, Function, ISI, Kerala Mathematics, Kut..taka, Mathemtical Modeling, Mathematical Societies - Calcutta, Madras and Allahabad, Numbers, Probability and Statistics, TIFR, Universities of Calcutta, Madras and Bombay, Vargaprakr.ti. India has been having a long tradition of mathematics. The contributions of Vedic and Jain mathematics are equally interesting. However, our discussion starts from 5th century onwards, so the important features of Indian mathematics are presented here in phases to make it simple. 500-1200 The period: 500-1200 is extremely interesting in the sense that this is known as the Golden (Siddha–ntic) period of Indian mathematics. It begins * The Key Note Address was delivered at the Indian Association for Cultivation of Science (Central Hall of IACS, Kolkata) organized on behalf of the M.C.