DOCSLIB.ORG

(Ecole Polytechnique, Palaiseau, France) Yves Andre

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
(Ecole Polytechnique, Palaiseau, France) Yves Andre PARTICIPANTS Emiliano Ambrosi (Ecole Polytechnique, Palaiseau, France) Yves Andre (CNRS, Paris, France) Dario Antolini (University of Rome, Italy) Stanislav Atanasov (Columbia University, NY, USA) Gregorio Baldi (University College London, UK) Jennifer Balakrishnan (Boston University, USA) Raphael Beuzart-Plessis (Institut de Mathematiques de Marseille, France) Fabrizio Barroero (Universit degli Studi Roma Tre, Italy) Florian Breuer (University of Newcastle, Australia) Anna Cadoret (Jussieu, Paris) Laura Capuano (University of Oxford, UK) Bumkyu Cho (Dongguk University, Seoul, South Korea) Kevin Kwan Chung (Columbia University, NY, USA) Giovanni Coppola (University of Salerno, Italy) Pietro Corvaja (University of Udine, Italy) Henri Darmon (McGill University, Montreal, Canada) Christopher Daw (University of Reading, UK) Alexis (Suki) Dasher (University of Minnesota, USA) Julian Lawrence Demeio (Scuola Normale Superiore, Pisa, Italy) Daniel Disegni (Ben Gurion University, Israel) Ick Sun Eum ( Dongguk University, Gyeongju City, South Korea) Rita Eppler-Goss (Ohio, USA) Bernadette Faye (Universite Cheikh Anta Diop De Dakar, Senegal) Ziyang Gao (Princeton University, USA) Michel Giacomini (University College, London, UK) Dorian Goldfeld (Columbia University, NY, USA) Giada Grossi (University College London, UK) Akash Jena (Indiana University, Bloomington, USA) Boris Kadets (MIT, Cambridge MA, USA) Sudesh Kaur Khanduja (IISER, Punjab, India) Ilya Khayutin (Princeton University, USA) Seema Kushwaha (Harish-Chandra Research Institute, Prayagraj, India) Shanta Laishram (Indian Statistical Institute, New Delhi, India) Brian Lawrence (University of Chicago, USA) Aaron Levin (Michigan State University, USA) Wen-Wei Li (Chinese Academy of Sciences, Beijing, China) Yifeng Liu (Yale University, Connecticut, USA) Yongxiao Lin (Ecole´ Polytechnique F´ed´eralede Lausanne, Switzerland) Joshua Males (Mathematical Institute, University of Cologne, Germany) David Masser (University of Basel, Switzerland) Vlad Alexandru Matei (University of California Irvine, USA) Giuseppe Melfi (Institut du Management de l'Information, Neuchatel, Switzerland) 2 Piotr Miska (Jagiellonian University in Krakow, Poland) Simone Munao (Elsevier, Amsterdam, Holland) Ritabrata Munshi (Tata Institute, Mumbai, India) Andrew Odesky (University of Michigan, USA) Ambrus Pal (Imperial College, London, UK) P´eterPal Pach (Budapest University of Technology and Economics, Hungary) Matteo Paganin (Sabanci University, Istanbul, Turkey) Laura Paladino (University of Pisa, Italy) Federico Pellarin (Universite Jean Monnet, Saint-Etienne, France) M. Pastora Revuelta (Escuela Tecnica Superior de Ingeneria de Edificacion, Sevilla, Spain) Maksym Radziwill (McGill University, Montreal, Canada) Larry Rolen (Vanderbilt University, TN, USA) Zev Rosengarten (Hebrew University of Jerusalem, Israel) Mohammad Sadek (Sabanci University, Istanbul, Turkey) Igor Shparlinski (University of New South Wales, Australia) Saurabh Kur Singh (Indian Statistical Institute, India) Christopher Skinner (Princeton University, USA) Lejla Smajlovic (University of Sarajevo, Sarajevo) Harry Smit (Utrecht University, Holland) Alexander Smith (Harvard University, Cambridge, USA) Kannan Soundararajan (Stanford University, USA) Lucien Szpiro (CUNY Graduate Center, NY, USA) Mohammed Taous (Moulay Ismail University, Errachidia, Morocco) Ye Tian (AMSS, Morningside Center of Mathematics, Beijing, China) Jacob Tsimerman (University of Toronto, Canada) Emmanuel Ullmo (IHES, Paris, France) Jeanine Van Order (Universitat Bielefeld, Germany) Carlo Viola (University of Pisa, Italy) Solomon Vishkautsan (Tel-Hai Academic College, Israel) Thomas Wright (Wofford University, SC, USA) Andrei Yafaev (University College, London, UK) Dong Sung Yoon (Pusan National University, South Korea) Umberto Zannier (Scuola Normale Superiore, Pisa, Italy) Robin Zhang (Columbia University, NY, USA) Shou-Wu Zhang (Princeton University, USA) Wei Zhang (MIT, Cambridge, MA, USA).
Load more

Recommended publications
  • 978-961-293-071-4.Pdf PUBLIC LECTURES 53
    CONTENTS 8th European Congress of Mathematics 20–26 June 2021 • Portorož, Slovenia PLENARY SPEAKERS 1 Presentation of Plenary, Invited, Public, Abel and Prize Speakers at the 8ECM Edited by INVITED SPEAKERS 11 Nino Bašic´ Ademir Hujdurovic´ Klavdija Kutnar THE EMS PRIZES 33 Tomaž Pisanski Vito Vitrih THE FELIX KLEIN PRIZE 43 Published by University of Primorska Press THE OTTO NEUGEBAUER PRIZE 45 Koper, Slovenia • www.hippocampus.si © 2021 University of Primorska ABEL LECTURE 49 Electronic Edition https://www.hippocampus.si/ISBN/978-961-293-071-4.pdf PUBLIC LECTURES 53 https://www.hippocampus.si/ISBN/978-961-293-072-1/index.html https://doi.org/10.26493/978-961-293-071-4 Kataložni zapis o publikaciji (CIP) pripravili v Narodni in univerzitetni knjižnici v Ljubljani COBISS.SI-ID = 65201411 ISBN 978-961-293-071-4 (pdf) ISBN 978-961-293-072-1 (html) PLENARY SPEAKERS 8th European Congress of Mathematics Plenary Speakers Peter Bühlmann Nirenberg, from the Courant Institute, New York University, 1994. Following his PhD, he has held the positions of Member of the Institute for Advanced ETH Zürich Study, Princeton, 1994–95; Habilitation à diriger des recherches, Université Pierre et Marie Curie-Paris VI, 1998; Harrington Faculty Fellow, The University of Texas at Austin, 2001–02; and Tenure Associate Professor, The University Biosketch of Texas at Austin, 2002–03. Since 2003, he has been an ICREA Research Peter Bühlmann is Professor of Mathematics and Professor at the Universitat Politècnica de Catalunya. He received the Kurt Statistics, and Director of Foundations of Data Science at ETH Zürich. He Friedrichs Prize, New York University, 1995, and is a Fellow of the American studied mathematics at ETH Zürich and received his doctoral degree in 1993 Mathematical Society, inaugural class of 2012.
    [Show full text]
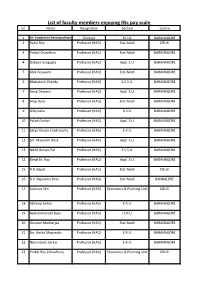
  • List of Faculty Members Enjoying Iisc Pay Scale Srl
    List of faculty members enjoying IISc pay scale Srl. Name Designation Section Centre 1 Sm. Sanghamitra Bandyopadhyay Director M.I.U. BARANAGORE 2 Rahul Roy Professor (HAG) Stat-Math DELHI 3 Probal Chaudhuri Professor (HAG) Stat-Math BARANAGORE 4 Debasis Sengupta Professor (HAG) Appl. S.U. BARANAGORE 5 Alok Goswami Professor (HAG) Stat-Math BARANAGORE 6 Bhabatosh Chanda Professor (HAG) E.C.S.U. BARANAGORE 7 Anup Dewanji Professor (HAG) Appl. S.U. BARANAGORE 8 Arup Bose Professor (HAG) Stat-Math BARANAGORE 9 Dilip Saha Professor (HAG) G.S.U. BARANAGORE 10 Palash Sarkar Professor (HAG) Appl. S.U. BARANAGORE 11 Satya Ranjan Chakravarty Professor (HAG) E.R.U. BARANAGORE 12 Sm. Mausumi Bose Professor (HAG) Appl. S.U. BARANAGORE 13 Nikhil Ranjan Pal Professor (HAG) E.C.S.U. BARANAGORE 14 Bimal Kr. Roy Professor (HAG) Appl. S.U. BARANAGORE 15 R.B. Bapat Professor (HAG) Stat-Math DELHI 16 B.V. Rajarama Bhat Professor (HAG) Stat-Math BANGALORE 17 Arunava Sen Professor (HAG) Economics & Planning Unit DELHI 18 Abhirup Sarkar Professor (HAG) E.R.U. BARANAGORE 19 Ayanendranath Basu Professor (HAG) I.S.R.U. BARANAGORE 20 Goutam Mukherjee Professor (HAG) Stat-Math BARANAGORE 21 Sm. Amita Majumder Professor (HAG) E.R.U. BARANAGORE 22 Nityananda Sarkar Professor (HAG) E.R.U. BARANAGORE 23 Prabal Roy Chowdhury Professor (HAG) Economics & Planning Unit DELHI 24 Subhamoy Maitra Professor (HAG) Appl. S.U. BARANAGORE 25 Tapas Samanta Professor (HAG) Appl. S.U. BARANAGORE 26 Abhay Gopal Bhatt Professor (HAG) Stat-Math DELHI 27 Atanu Biswas Professor (HAG) Appl. S.U.
    [Show full text]
  • Fundamental Algebraic Geometry
    http://dx.doi.org/10.1090/surv/123 hematical Surveys and onographs olume 123 Fundamental Algebraic Geometry Grothendieck's FGA Explained Barbara Fantechi Lothar Gottsche Luc lllusie Steven L. Kleiman Nitin Nitsure AngeloVistoli American Mathematical Society U^VDED^ EDITORIAL COMMITTEE Jerry L. Bona Peter S. Landweber Michael G. Eastwood Michael P. Loss J. T. Stafford, Chair 2000 Mathematics Subject Classification. Primary 14-01, 14C20, 13D10, 14D15, 14K30, 18F10, 18D30. For additional information and updates on this book, visit www.ams.org/bookpages/surv-123 Library of Congress Cataloging-in-Publication Data Fundamental algebraic geometry : Grothendieck's FGA explained / Barbara Fantechi p. cm. — (Mathematical surveys and monographs, ISSN 0076-5376 ; v. 123) Includes bibliographical references and index. ISBN 0-8218-3541-6 (pbk. : acid-free paper) ISBN 0-8218-4245-5 (soft cover : acid-free paper) 1. Geometry, Algebraic. 2. Grothendieck groups. 3. Grothendieck categories. I Barbara, 1966- II. Mathematical surveys and monographs ; no. 123. QA564.F86 2005 516.3'5—dc22 2005053614 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy a chapter for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given. Republication, systematic copying, or multiple reproduction of any material in this publication is permitted only under license from the American Mathematical Society. Requests for such permission should be addressed to the Acquisitions Department, American Mathematical Society, 201 Charles Street, Providence, Rhode Island 02904-2294, USA.
    [Show full text]
  • Elliptic Surfaces and Arithmetic Equidistribution for $\Mathbb {R
    ELLIPTIC SURFACES AND ARITHMETIC EQUIDISTRIBUTION FOR R-DIVISORS ON CURVES LAURA DE MARCO AND NIKI MYRTO MAVRAKI Abstract. Suppose E → B is a non-isotrivial elliptic surface defined over a number field, for smooth projective curve B. Let k denote the function field Q(B) and E the associated elliptic curve over k. In this article, we construct adelically metrized R-divisors DX on the base curve B over a number field, for each X ∈ E(k) ⊗ R. We prove non-degeneracy of the Arakelov-Zhang intersection numbers DX · DY , as a biquadratic form on E(k) ⊗ R. As a consequence, we have the following Bogomolov-type statement for the N´eron- Tate height functions on the fibers Et(Q) of E over t ∈ B(Q): given points P1,...,Pm ∈ E(k) with m ≥ 2, there exist a non-repeating infinite sequence tn ∈ B(Q) and small- ′ ′ ′ height perturbations Pi,tn ∈ Etn (Q) of specializations Pi,tn so that the set {P1,tn ,...,Pm,tn } satisfies at least two independent linear relations for all n, if and only if the points P1,...,Pm are linearly dependent in E(k). This gives a new proof of results of Masser and Zannier [MZ1, MZ2] and of Barroero and Capuano [BC] and extends our earlier results [DM]. We also prove a general equidistribution theorem for adelically metrized R-divisors on curves (over a number field), extending the equidistribution theorems of Chambert-Loir, Thuillier, and Yuan [CL1, Th, Yu], and using results of Moriwaki [Mo2]. 1. Introduction Suppose E → B is an elliptic surface defined over a number field K.
    [Show full text]
  • Publications of Shou-Wu Zhang
    Publications of Shou-Wu Zhang 1. Gerd Faltings, Lectures on the arithmetic Riemann-Roch theorem. Notes taken by Shouwu Zhang. Annals of Mathematics Studies, 127. (1992). x+100 pp. amazon 2. Positive line bundles on arithmetic surfaces. Ann. of Math. (2) 136 (1992), no. 3, pp 569{587. pdf 3. Admissible pairing on a curve. Invent. Math. 112 (1993), no. 1, pp 171{193. pdf 4. Geometric reductivity at Archimedean places. Internat. Math. Res. No- tices 1994, no. 10, 425 ff., approx. 9 pp. pdf 5. Positive line bundles on arithmetic varieties. J. Amer. Math. Soc. 8 (1995), no. 1, pp 187{221. pdf 6. Small points and adelic metrics. J. Algebraic Geom. 4 (1995), no. 2, 28100 pdf 7. Heights and reductions of semi-stable varieties. Compositio Math. 104 (1996), no. 1, pp 77{105. pdf 8. (with Lucien Szpiro, Emmanuel Ullmo) Equir´epartition´ des petits points. Invent. Math. 127 (1997), no. 2, pp 337{347. pdf 9. Heights of Heegner cycles and derivatives of L-series. Invent. Math. 130 (1997), no. 1, pp 99{152. pdf 10. Equidistribution of small points on abelian varieties. Ann. of Math. (2) 147 (1998), no. 1, pp 159{165. pdf 11. Small points and Arakelov theory. Proc. of ICM, Doc. Math. 1998, Extra Vol. II, pp 217{225 (electronic). pdf 12. (with Dorian Goldfeld) The holomorphic kernel of the Rankin-Selberg con- volution. Asian J. Math. 3 (1999), no. 4, pp 729{747. pdf 13. Distribution of almost division points. Duke Math. J. 103 (2000), no. 1, pp 39{46. pdf 14.
    [Show full text]
  • NÉRON MODELS 1. Introduction Néron Models Were Introduced by André Néron (1922-1985) in His Seminar at the IHES in 1961. He
    NERON´ MODELS DINO LORENZINI Abstract. N´eronmodels were introduced by Andr´eN´eronin his seminar at the IHES in 1961. This article gives a brief survey of past and recent results in this very useful theory. KEYWORDS N´eronmodel, weak N´eronmodel, abelian variety, group scheme, elliptic curve, semi-stable reduction, Jacobian, group of components. MATHEMATICS SUBJECT CLASSIFICATION: 14K15, 11G10, 14L15 1. Introduction N´eronmodels were introduced by Andr´eN´eron(1922-1985) in his seminar at the IHES in 1961. He gave a summary of his results in a 1961 Bourbaki seminar [81], and a longer summary was published in 1962 in Crelle's journal [82]. N´eron'sown full account of his theory is found in [83]. Unfortunately, this article1 is not completely written in the modern language of algebraic geometry. N´eron'sinitial motivation for studying models of abelian varieties was his study of heights (see [84], and [56], chapters 5 and 10-12, for a modern account). In [83], N´eronmentions his work on heights2 by referring to a talk that he gave at the International Congress in Edinburgh in 1958. I have been unable to locate a written version of this talk. A result attributed to N´eronin [54], Corollary 3, written by Serge Lang in 1963, might be a result that N´erondiscussed in 1958. See also page 438 of [55]. There is a vast literature on the theory of N´eronmodels. The first mention of N´eron models completely in the language of schemes may be in an article of Jean-Pierre Serre at the International Congress in Stockholm in 1962 ([94], page 195).
    [Show full text]
  • OF the AMERICAN MATHEMATICAL SOCIETY 157 Notices February 2019 of the American Mathematical Society
    ISSN 0002-9920 (print) ISSN 1088-9477 (online) Notices ofof the American MathematicalMathematical Society February 2019 Volume 66, Number 2 THE NEXT INTRODUCING GENERATION FUND Photo by Steve Schneider/JMM Steve Photo by The Next Generation Fund is a new endowment at the AMS that exclusively supports programs for doctoral and postdoctoral scholars. It will assist rising mathematicians each year at modest but impactful levels, with funding for travel grants, collaboration support, mentoring, and more. Want to learn more? Visit www.ams.org/nextgen THANK YOU AMS Development Offi ce 401.455.4111 [email protected] A WORD FROM... Robin Wilson, Notices Associate Editor In this issue of the Notices, we reflect on the sacrifices and accomplishments made by generations of African Americans to the mathematical sciences. This year marks the 100th birthday of David Blackwell, who was born in Illinois in 1919 and went on to become the first Black professor at the University of California at Berkeley and one of America’s greatest statisticians. Six years after Blackwell was born, in 1925, Frank Elbert Cox was to become the first Black mathematician when he earned his PhD from Cornell University, and eighteen years later, in 1943, Euphemia Lofton Haynes would become the first Black woman to earn a mathematics PhD. By the late 1960s, there were close to 70 Black men and women with PhDs in mathematics. However, this first generation of Black mathematicians was forced to overcome many obstacles. As a Black researcher in America, segregation in the South and de facto segregation elsewhere provided little access to research universities and made it difficult to even participate in professional societies.
    [Show full text]
  • Henri Darmon
    Henri Darmon Address: Dept of Math, McGill University, Burnside Hall, Montreal, PQ. E-mail: [email protected] Web Page: http://www.math.mcgill.ca/darmon Telephone: Work (514) 398-2263 Home: (514) 481-0174 Born: Oct. 22, 1965, in Paris, France. Citizenship: Canadian, French, and Swiss. Education: 1987. B.Sc. Mathematics and Computer Science, McGill University. 1991. Ph.D. Mathematics, Harvard University. Thesis: Refined class number formulas for derivatives of L-series. University Positions: 1991-1994. Princeton University, Instructor. 1994-1996. Princeton University, Assistant Professor. 1994-1997. McGill University, Assistant Professor. 1997-2000. McGill University, Associate Professor. 2000- . McGill University, Professor. 2005-2019. James McGill Professor, McGill University. Other positions: 1991-1994. Cercheur hors Qu´ebec, CICMA. 1994- . Chercheur Universitaire, CICMA. 1998- . Director, CICMA (Centre Interuniversitaire en Calcul Math´ematique Alg´ebrique). 1999- . Member, CRM (Centre de Recherches Math´ematiques). 2005-2014. External member, European network in Arithmetic Geometry. Visiting Positions: 1991. IHES, Paris. 1995. Universit´a di Pavia. 1996. Visiting member, MSRI, Berkeley. 1996. Visiting professor and guest lecturer, University of Barcelona. 1997. Visiting Professor, Universit´e Paris VI (Jussieu). 1997. Visitor, Institut Henri Poincar´e. 1998. Visiting Professor and NachDiplom lecturer, ETH, Zuric¨ h. 1999. Visiting professor, Universit`a di Pavia. 2001. Visiting professor, Universit`a di Padova. 2001. Korea Institute for Advanced Study. 2002. Visiting professor, RIMS and Saga University (Japan). 1 2003. Visiting Professor, Universit´e Paris VI, Paris. 2003. Visiting professor, Princeton University. 2004. Visiting Professor, Universit´e Paris VI, Paris. 2006. Visiting Professor, CRM, Barcelona, Spain. 2008. Visiting Professor, Universit´e Paris-Sud (Orsay).
    [Show full text]
  • Dynamics on Berkovich Spaces in Low Dimensions
    Dynamics on Berkovich Spaces in Low Dimensions Mattias Jonsson Contents 1 Introduction..................................................................................... 205 2 Tree Structures ................................................................................. 220 3 The Berkovich Affine and Projective Lines ................................................... 236 4 Action by Polynomial and Rational Maps .................................................... 253 5 Dynamics of Rational Maps in One Variable ................................................. 270 6 The Berkovich Affine Plane Over a Trivially Valued Field .................................. 283 7 The Valuative Tree at a Point .................................................................. 297 8 Local Plane Polynomial Dynamics ............................................................ 328 9 The Valuative Tree at Infinity.................................................................. 335 10 Plane Polynomial Dynamics at Infinity ....................................................... 352 References .......................................................................................... 361 1 Introduction The goal of these notes is twofold. First, I’d like to describe how Berkovich spaces enter naturally in certain instances of discrete dynamical systems. In particular, I will try to show how my own work with Charles Favre [FJ07, FJ11]onvaluative dynamics relates to the dynamics of rational maps on the Berkovich projective line as initiated by Juan Rivera-Letelier
    [Show full text]
  • Rational Points in Periodic Analytic Sets and the Manin-Mumford Conjecture
    Rational points in periodic analytic sets and the Manin-Mumford conjecture Jonathan Pila & Umberto Zannier Abstract. We present a new proof of the Manin-Mumford conjecture about torsion points on algebraic subvarieties of abelian varieties. Our principle, which admits other applications, is to view torsion points as rational points on a complex torus and then compare (i) upper bounds for the number of rational points on a transcendental analytic variety (Bombieri-Pila-Wilkie) and (ii) lower bounds for the degree of a torsion point (Masser), after taking conjugates. In order to be able to deal with (i), we discuss (Thm. 2.1) the semi-algebraic curves contained in an analytic variety supposed invariant for translations by a full lattice, which is a topic with some independent motivation. CAPITOLO DELLA SCIENZA: Teoria dei Numeri (n. 6) KEY WORDS: Torsion points on algebraic varieties; Rational points on analytic varieties; Conjecture of Manin-Mumford. §1. Introduction The so-called Manin-Mumford conjecture was raised independently by Manin and Mumford and first proved by Raynaud [R] in 1983; its original form stated that a curve C (over C) of genus ≥ 2, embedded in its Jacobian J, can contain only finitely many torsion points (relative of course to the Jacobian group-structure). Raynaud actually considered the more general case when C is embedded in any abelian variety. Soon afterwards, Raynaud [R2] produced a further significant generalization, replacing C and J respectively by a subvariety X in an abelian variety A; in this situation he proved that if X contains a Zariski-dense set of torsion points, then X is a translate of an abelian subvariety of A by a torsion point.
    [Show full text]
  • A Dynamical Shafarevich Theorem for Rational Maps Over Number Fields and Function Fields
    A DYNAMICAL SHAFAREVICH THEOREM FOR RATIONAL MAPS OVER NUMBER FIELDS AND FUNCTION FIELDS LUCIEN SZPIRO AND LLOYD WEST Abstract. We prove a dynamical Shafarevich theorem on the finiteness of the set of isomorphism classes of rational maps with fixed degeneracies. More precisely, fix an integer d ≥ 2 and let K be either a number field or the function field of a curve X over a field k, where k is of characteristic zero or p > 2d − 2 that is either algebraically closed or finite. Let S be a finite set of places of K. We prove the finiteness of the set of isomorphism classes of rational maps over K with a natural kind of good reduction outside of S. We also prove auxiliary 1 results on finiteness of reduced effective divisors in PK with good reduction outside of S and on the existence of global models for rational maps. Dedicated to Joseph Silverman on his 60th birthday 1. Introduction 1.1. Rational maps and dynamical systems. Let K be a field. By a rational 1 1 map of degree d over K, we mean a separable morphism f : PK ! PK defined over K. Note that such an f can be thought of as an element of the rational function field K(z); alternatively, a rational map may be written f = [f1(x; y): f2(x; y)] for a pair f1; f2 2 k[x; y] of homogeneous polynomials of degree d. The behavior of rational maps under iteration has been intensively studied - both over C (see [M] for an overview), and more recently over fields of an arithmetic nature, such as Q, Qp or Fp(t) (see [S4] for an overview).
    [Show full text]
  • The Paradox of the Proof | Project Wordsworth
    The Paradox of the Proof | Project Wordsworth Home | About the Authors If you enjoy this story, we ask that you consider paying for it. Please see the payment section below. The Paradox of the Proof By Caroline Chen MAY 9, 2013 n August 31, 2012, Japanese mathematician Shinichi Mochizuki posted four O papers on the Internet. The titles were inscrutable. The volume was daunting: 512 pages in total. The claim was audacious: he said he had proved the ABC Conjecture, a famed, beguilingly simple number theory problem that had stumped mathematicians for decades. Then Mochizuki walked away. He did not send his work to the Annals of Mathematics. Nor did he leave a message on any of the online forums frequented by mathematicians around the world. He just posted the papers, and waited. Two days later, Jordan Ellenberg, a math professor at the University of Wisconsin- Madison, received an email alert from Google Scholar, a service which scans the Internet looking for articles on topics he has specified. On September 2, Google Scholar sent him Mochizuki’s papers: You might be interested in this. http://projectwordsworth.com/the-paradox-of-the-proof/[10/03/2014 12:29:17] The Paradox of the Proof | Project Wordsworth “I was like, ‘Yes, Google, I am kind of interested in that!’” Ellenberg recalls. “I posted it on Facebook and on my blog, saying, ‘By the way, it seems like Mochizuki solved the ABC Conjecture.’” The Internet exploded. Within days, even the mainstream media had picked up on the story. “World’s Most Complex Mathematical Theory Cracked,” announced the Telegraph.
    [Show full text]