DOCSLIB.ORG

Member's Copy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Member's Copy ISSN: 0025-5742 THE MATHEMATICS STUDENT Volume 84, Numbers 1-2, January-June, (2015) (Issued: May, 2015) - Editor-in-Chief J. R. PATADIA EDITORScopy Bruce Berndt George Andrews M: Ram Murty N: K: Thakare Satya Deo Gadadhar Misra B: Sury Kaushal Verma Krishnaswami Alladi S: K: Tomar Subhash J: Bhattcirculation L: Sunil Chandran M: M: Shikare C: S: Aravinda A: S: Vasudeva Murthy Indranil Biswas Timothyfor Huber T: S: S: R: K: Rao Clare D0Member'sCruz Atul Dixit not PUBLISHED BY THE INDIAN MATHEMATICAL SOCIETY www.indianmathsociety.org.in THE MATHEMATICS STUDENT Edited by J. R. PATADIA In keeping with the current periodical policy, THE MATHEMATICS STUDENT will seek to publish material of interest not just to mathematicians with specialized interest but to the postgraduate students and teachers of mathematics in India. With this in view, it will ordinarily publish material of the following type: 1. the texts (written in a way accessible to students) of the Presidential Addresses, the Plenary talks and the Award Lectures delivered at the Annual Conferences. 2. general survey articles, popular articles, expository papers, Book-Reviews. 3. problems and solutions of the problems, 4. new, clever proofs of theorems that graduate / undergraduate students might see in their course work, 5. research papers (not highly technical, but of interest to larger readership) and 6. articles that arouse curiosity and interest for learning mathematics among readers and motivate them for doing mathematics. Articles of the above type are invited for publication in THE MATHEMATICS STUDENT. Manuscripts intended for publication should be submitted online in the LATEX and .pdf file including figures and tables to the Editor- J. R. Patadia on E-mail: [email protected] Manuscripts (including bibliographies, tables, etc.) should be typed double spaced on A4 size paper with 1 inch (2.5 cm.) margins on all sides with font size 10 pt. in LATEX. Sections should appear in the following order: Title Page, Abstract, Text, Notes and References. Comments or replies to previouslycopy published articles should also follow this format with the exception of abstracts. In LATEX, the following preamble be used as is required by the Press: n documentclass[10 pt,a4paper,twoside,reqno]famsartg n usepackage famsfonts, amssymb, amscd, amsmath, enumerate, verbatim, calcg n renewcommandfn baselinestretchgf1.2g n textwidth=12.5 cm circulation n textheight=20 cm n topmargin=0.5 cm n oddsidemargin=1 cm for n evensidemargin=1 cm n pagestyleMember'sfplaing The details are available on Indian Mathematical Society website: www.indianmath society.org.in not Authors of articles / research papers printed in the the Mathematics Student as well as in the Journal shall be entitled to receive a soft copy (PDF file with watermarked \Author's copy") of the paper published. There are no page charges. However, if author(s) (whose paper is accepted for publication in any of the IMS periodicals) is (are) unable to send the LaTeX file of the accepted paper, then a charge Rs. 100 (US $ 10) per page will be levied for LaTex typesetting charges. All business correspondence should be addressed to S. K. Nimbhorkar, Treasurer, Indian Mathematical Society, Dept. of Mathematics, Dr. B. A. M. University, Aurangabad - 431 004 (Maharashtra), India. E-mail: [email protected] Copyright of the published articles lies with the Indian Mathematical Society. In case of any query, the Editor may be contacted. ISSN: 0025-5742 THE MATHEMATICS STUDENT Volume 84, Numbers 1-2, January-June, (2015) (Issued: May, 2015) - Editor-in-Chief J. R. PATADIA copy EDITORS Bruce Berndt George Andrews M: Ram Murty N: K: Thakare Satya Deo Gadadhar Misra B: Sury Kaushal Vermacirculation Krishnaswami Alladi S: K: Tomar Subhash J: Bhatt L: Sunil Chandran M: M: Shikare C: Sfor: Aravinda A: S: Vasudeva Murthy IndranilMember's Biswas Timothy Huber T: S: S: R: K: Rao 0 Clare D Cruz not Atul Dixit PUBLISHED BY THE INDIAN MATHEMATICAL SOCIETY www.indianmathsociety.org.in ISSN: 0025-5742 ii c THE INDIAN MATHEMATICAL SOCIETY,- 2015. This volume or any part thereof may not be reproduced in any form without the written permission of the publisher. copy This volume is not to be sold outside the Country to which it is consigned by the Indian Mathematical Society. circulation Member's copy is strictly for personal use. It is not intended for sale or circular.for Member's not Published by Prof. N. K. Thakare for the Indian Mathematical Society, type set by J. R. Patadia at 5, Arjun Park, Near Patel Colony, Behind Dinesh Mill, Shivanand Marg, Vadodara - 390 007 and printed by Dinesh Barve at Parashuram Process, Shed No. 1246/3, S. No. 129/5/2, Dalviwadi Road, Barangani Mala, Wadgaon Dhayari, Pune 411 041 (India). Printed in India. The Mathematics Student ISSN: 0025-5742 Vol. 84, Nos. 1-2, January-June, (2015) CONTENTS 1. S. G. Dani Prizes, recognitions and promotion of mathematics. 01-06 2. S. G. Dani Dynamics of Numbers. 07-21 3. Ritabrata On some recent applications of circle method. 23-38 Munshi 4. Ajit Iqbal How permutations, partitions, projective 39-52 Singh representations and positive maps entangle well for quantum information theory. 5. Pablo Andr´es A generating function related to π. 53-56 Panzone 6. Jay Praksh On a type of Sasakian manifolds- admitting a 57-67 Singh quarter symmetric non-metric connection. 1 7. Amrik Singh Deriving Forsyth-Glaisher type series for π 69-86 Nimbran and catalan's constant by an elementary method. 8. Dinesh On escaping sets of some families of entire functions 87-94 Kumar and Dynamics ofcopy composite entire functions. 9. Priti Singh Existence of reduction of ideals over semi-local 95-104 and Shiv rings. Datt Kumar 10. Manjil P. A study of the Crank function in Ramanujans 105-121 Saikia lost notebook. circulation 11. Josef Bukac Integrability of continuous functions. 123-127 12. M. Ram Murty A very simple proof of Stirlings formula. 129-133 and Kannappan Sampath for 13. ManishaMember's Diophantine equations of the form 135-155 Kulkarni f(x) = g(y) - an exposition and B. Sury 14. - notProblem Section 157-161 ******* - copy circulation for Member's not iv The Mathematics Student ISSN: 0025-5742 Vol. 84, Nos. 1-2, January-June, (2015) EDITORIAL NOTE The publication of the Mathematics Student began from 1933 as a quarterly to serve the students and teachers of mathematics. In fact, one observes the following sentence clearly printed on the front cover page of each volume of The Mathematics Student till 1952 A Quarterly Dedicated to the Service of Students and Teachers of Mathematics in India and notes that it used to have in its contents sections on Questions and solutions, Mathematical notes, Classroom notes, Book-Reviews, etc. right from the beginning till around mid-fifties, but it appears to have gradually disappeared- then after. During the past couple of years, it was widely felt among some of the well-wishers of the Indian Mathematical Society (the IMS) that the Mathematics Student has become a research level journal with no appeal to students; and it was suggested that since the IMS has no such journal for students nor perhaps is there any such journal published in India, the IMS seriously should address this deficiency. The thread was picked up by the Council of the Society, an Editorial Boardcopy for the Mathematics Student is now formed and, as a humble beginning, we are happy to resume the Problem Section beginning with this issue. The Council is aware that the success to make this periodical more relevant, acc- sessible and accptable to the larger section of mathematical community, our students and teachers of mathematics, lies in thecirculation active participation from the entire mathemat- ical community of the motherland and earnestly appeals and invites one and all for the active participation to serve the cause of mathematics in this way. It may be noted here that for making it feasible for everyonefor to participate, the soft copy of the Mathematics Student isMember's made available, for free open access to all, on Society's website: www.indianmathsociety.org.in not - copy circulation for Member's not vi The Mathematics Student ISSN: 0025-5742 Vol. 84, Nos. 1-2, January-June (2015), 01-06 PRIZES, RECOGNITIONS AND PROMOTION OF MATHEMATICS* S. G. DANI Manjul Bhargava was awarded the Fields Medal this year, at the inaugural function of the International Congress of Mathematicians at Seoul, South Korea, on 13 August 2014. Joyous messages were exchanged, following the announcement, by the Indian mathematical community and the Indian people in general. Many mathematicians from India present at the function wrote- home enthusiastically from the venue with whatever additional information they could gather. Many newspapers and magazines came out with special write-ups with different levels of outreach. It was an historic occasion, with a mathematician of Indian origin receiving the medal for the first time. Let me begin this talk by recording my heartiest congratulations to Prof. Manjulcopy Bhargava for the achievement. In fact the occasion was historic in more ways. Maryam Mirzakhani, another concurrent recipient of the medal, is the first woman to receive the honour. She is also the first mathematician from Iran to be awarded the Fields Medal. My ardent felicitations to her for the accomplishment; may she inspire our daughters and granddaughters to excel in mathematics.circulation The Fields Medal had been the unique coveted Prize in mathematics for a long time**, and has often been described loosely as the \Nobel Prize in mathematics" (the Nobel Prize not being awardedfor in mathematics), notwithstanding the vast differenceMember's between the prize amounts of the two. In recent years however there have been other significant new prizes (including some with large monetary not components).
Load more

Recommended publications
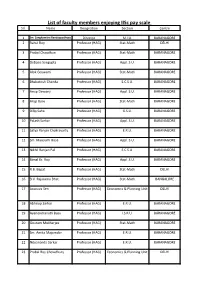
  • List of Faculty Members Enjoying Iisc Pay Scale Srl
    List of faculty members enjoying IISc pay scale Srl. Name Designation Section Centre 1 Sm. Sanghamitra Bandyopadhyay Director M.I.U. BARANAGORE 2 Rahul Roy Professor (HAG) Stat-Math DELHI 3 Probal Chaudhuri Professor (HAG) Stat-Math BARANAGORE 4 Debasis Sengupta Professor (HAG) Appl. S.U. BARANAGORE 5 Alok Goswami Professor (HAG) Stat-Math BARANAGORE 6 Bhabatosh Chanda Professor (HAG) E.C.S.U. BARANAGORE 7 Anup Dewanji Professor (HAG) Appl. S.U. BARANAGORE 8 Arup Bose Professor (HAG) Stat-Math BARANAGORE 9 Dilip Saha Professor (HAG) G.S.U. BARANAGORE 10 Palash Sarkar Professor (HAG) Appl. S.U. BARANAGORE 11 Satya Ranjan Chakravarty Professor (HAG) E.R.U. BARANAGORE 12 Sm. Mausumi Bose Professor (HAG) Appl. S.U. BARANAGORE 13 Nikhil Ranjan Pal Professor (HAG) E.C.S.U. BARANAGORE 14 Bimal Kr. Roy Professor (HAG) Appl. S.U. BARANAGORE 15 R.B. Bapat Professor (HAG) Stat-Math DELHI 16 B.V. Rajarama Bhat Professor (HAG) Stat-Math BANGALORE 17 Arunava Sen Professor (HAG) Economics & Planning Unit DELHI 18 Abhirup Sarkar Professor (HAG) E.R.U. BARANAGORE 19 Ayanendranath Basu Professor (HAG) I.S.R.U. BARANAGORE 20 Goutam Mukherjee Professor (HAG) Stat-Math BARANAGORE 21 Sm. Amita Majumder Professor (HAG) E.R.U. BARANAGORE 22 Nityananda Sarkar Professor (HAG) E.R.U. BARANAGORE 23 Prabal Roy Chowdhury Professor (HAG) Economics & Planning Unit DELHI 24 Subhamoy Maitra Professor (HAG) Appl. S.U. BARANAGORE 25 Tapas Samanta Professor (HAG) Appl. S.U. BARANAGORE 26 Abhay Gopal Bhatt Professor (HAG) Stat-Math DELHI 27 Atanu Biswas Professor (HAG) Appl. S.U.
    [Show full text]
  • MAT 5930. Analysis for Teachers
    MAT 5930. Analysis for Teachers. Wm C Bauldry [email protected] Fall ’13 Wm C Bauldry ([email protected]) MAT 5930. Analysis for Teachers. Fall ’13 1 / 147 Nordkapp, Norway. Today Wm C Bauldry ([email protected]) MAT 5930. Analysis for Teachers. Fall ’13 2 / 147 Introduction and Calculus Considered 1 Course Introduction (Class page, Course Info, Syllabus) 2 Calculus Considered 1 A Standard Freshman Calculus Course B Topics List: MAT 1110; MAT 1120 B Refer to texts by Thomas (traditional), Stewart (very popular, but. ), and Hughes-Hallett, et al, or Ostebee & Zorn (“reform”). B Historical: L’Hopital’sˆ Analyse des Infiniment Petits pour l’Intelligence des Lignes Courbes, Cauchy’s Cours d’Analyse, and Granville, Smith, & Longley’s Elements of the Differential and Integral Calculus 2 An AP Calculus Course(AB,BC) 1 Functions, Graphs, and Limits Representations, one-to-one, onto, inverses, analysis of graphs, limits of functions, asymptotic behavior, continuity, uniform continuity 2 Derivatives Concept, definitions, interpretations, at a point, as a function, second derivative, applications, computation, numerical approx. 3 Integrals Concept, definitions, interpretations, properties, Fundamental Theorem, applications, techniques, applications, numerical approx. Wm C Bauldry ([email protected]) MAT 5930. Analysis for Teachers. Fall ’13 3 / 147 Calculus Considered 2 (Calculus Considered) 3 Calculus Problems x1 Precalculus material: function, induction, summation, slope, trigonometry x2 Limits and Continuity: Squeeze Theorem, discontinuity, removable discontinuity, different interpretations of limit expressions x3 Derivatives: trigonometric derivatives, power rule, indirect methods, Newton’s method, Mean Value Theorem,“Racetrack Principle” x4 Integration: Fundamental Theorem, Riemann sums, parts, multiple integrals x5 Infinite Series: geometric, integrals and series, partial fractions, convergence tests (ratio, root, comparison, integral), Taylor & Maclaurin Wm C Bauldry ([email protected]) MAT 5930.
    [Show full text]
  • Profile Book 2017
    MATH MEMBERS A. Raghuram Debargha Banerjee Neeraj Deshmukh Sneha Jondhale Abhinav Sahani Debarun Ghosh Neha Malik Soumen Maity Advait Phanse Deeksha Adil Neha Prabhu Souptik Chakraborty Ajith Nair Diganta Borah Omkar Manjarekar Steven Spallone Aman Jhinga Dileep Alla Onkar Kale Subham De Amit Hogadi Dilpreet Papia Bera Sudipa Mondal Anindya Goswami Garima Agarwal Prabhat Kushwaha Supriya Pisolkar Anisa Chorwadwala Girish Kulkarni Pralhad Shinde Surajprakash Yadav Anup Biswas Gunja Sachdeva Rabeya Basu Sushil Bhunia Anupam Kumar Singh Jyotirmoy Ganguly Rama Mishra Suvarna Gharat Ayan Mahalanobis Kalpesh Pednekar Ramya Nair Tathagata Mandal Ayesha Fatima Kaneenika Sinha Ratna Pal Tejas Kalelkar Baskar Balasubramanyam Kartik Roy Rijubrata Kundu Tian An Wong Basudev Pattanayak Krishna Kaipa Rohit Holkar Uday Bhaskar Sharma Chaitanya Ambi Krishna Kishore Rohit Joshi Uday Jagadale Chandrasheel Bhagwat Makarand Sarnobat Shane D'Mello Uttara Naik-Nimbalkar Chitrabhanu Chaudhuri Manidipa Pal Shashikant Ghanwat Varun Prasad Chris John Manish Mishra Shipra Kumar Venkata Krishna Debangana Mukherjee Milan Kumar Das Shuvamkant Tripathi Visakh Narayanan Debaprasanna Kar Mousomi Bhakta Sidharth Vivek Mohan Mallick Compiling, Editing and Design: Shanti Kalipatnapu, Kranthi Thiyyagura, Chandrasheel Bhagwat, Anisa Chorwadwala Art on the Cover: Sinjini Bhattacharjee, Arghya Rakshit Photo Courtesy: IISER Pune Math Members 2017 IISER Pune Math Book WELCOME MESSAGE BY COORDINATOR I have now completed over five years at IISER Pune, and am now in my sixth and possibly final year as Coordinator for Mathematics. I am going to resist the temptation of evaluating myself as to what I have or have not accomplished as head of mathematics, although I do believe that it’s always fruitful to take stock, to become aware of one’s strengths, and perhaps even more so of one’s weaknesses, especially when the goal we have set for ourselves is to become a strong force in the international world of Mathematics.
    [Show full text]
  • Scheme of Instruction 2021 - 2022
    Scheme of Instruction Academic Year 2021-22 Part-A (August Semester) 1 Index Department Course Prefix Page No Preface : SCC Chair 4 Division of Biological Sciences Preface 6 Biological Science DB 8 Biochemistry BC 9 Ecological Sciences EC 11 Neuroscience NS 13 Microbiology and Cell Biology MC 15 Molecular Biophysics Unit MB 18 Molecular Reproduction Development and Genetics RD 20 Division of Chemical Sciences Preface 21 Chemical Science CD 23 Inorganic and Physical Chemistry IP 26 Materials Research Centre MR 28 Organic Chemistry OC 29 Solid State and Structural Chemistry SS 31 Division of Physical and Mathematical Sciences Preface 33 High Energy Physics HE 34 Instrumentation and Applied Physics IN 38 Mathematics MA 40 Physics PH 49 Division of Electrical, Electronics and Computer Sciences (EECS) Preface 59 Computer Science and Automation E0, E1 60 Electrical Communication Engineering CN,E1,E2,E3,E8,E9,MV 68 Electrical Engineering E0,E1,E4,E5,E6,E8,E9 78 Electronic Systems Engineering E0,E2,E3,E9 86 Division of Mechanical Sciences Preface 95 Aerospace Engineering AE 96 Atmospheric and Oceanic Sciences AS 101 Civil Engineering CE 104 Chemical Engineering CH 112 Mechanical Engineering ME 116 Materials Engineering MT 122 Product Design and Manufacturing MN, PD 127 Sustainable Technologies ST 133 Earth Sciences ES 136 Division of Interdisciplinary Research Preface 139 Biosystems Science and Engineering BE 140 Scheme of Instruction 2021 - 2022 2 Energy Research ER 144 Computational and Data Sciences DS 145 Nanoscience and Engineering NE 150 Management Studies MG 155 Cyber Physical Systems CP 160 Scheme of Instruction 2020 - 2021 3 Preface The Scheme of Instruction (SoI) and Student Information Handbook (Handbook) contain the courses and rules and regulations related to student life in the Indian Institute of Science.
    [Show full text]
  • IISER AR PART I A.Cdr
    dm{f©H$ à{VdoXZ Annual Report 2016-17 ^maVr¶ {dkmZ {ejm Ed§ AZwg§YmZ g§ñWmZ nwUo Indian Institute of Science Education and Research Pune XyaX{e©Vm Ed§ bú` uCƒV‘ j‘Vm Ho$ EH$ Eogo d¡km{ZH$ g§ñWmZ H$s ñWmnZm {Og‘| AË`mYw{ZH$ AZwg§YmZ g{hV AÜ`mnZ Ed§ {ejm nyU©ê$n go EH$sH¥$V hmo& u{Okmgm Am¡a aMZmË‘H$Vm go `wº$ CËH¥$ï> g‘mH$bZmË‘H$ AÜ`mnZ Ho$ ‘mÜ`m‘ go ‘m¡{bH$ {dkmZ Ho$ AÜ``Z H$mo amoMH$ ~ZmZm& ubMrbo Ed§ Agr‘ nmR>çH«$‘ VWm AZwg§YmZ n[a`moOZmAm| Ho$ ‘mÜ`‘ go N>moQ>r Am`w ‘| hr AZwg§YmZ joÌ ‘| àdoe& Vision & Mission uEstablish scientific institution of the highest caliber where teaching and education are totally integrated with state-of-the-art research uMake learning of basic sciences exciting through excellent integrative teaching driven by curiosity and creativity uEntry into research at an early age through a flexible borderless curriculum and research projects Annual Report 2016-17 Correct Citation IISER Pune Annual Report 2016-17, Pune, India Published by Dr. K.N. Ganesh Director Indian Institute of Science Education and Research Pune Dr. Homi J. Bhabha Road Pashan, Pune 411 008, India Telephone: +91 20 2590 8001 Fax: +91 20 2025 1566 Website: www.iiserpune.ac.in Compiled and Edited by Dr. Shanti Kalipatnapu Dr. V.S. Rao Ms. Kranthi Thiyyagura Photo Courtesy IISER Pune Students and Staff © No part of this publication be reproduced without permission from the Director, IISER Pune at the above address Printed by United Multicolour Printers Pvt.
    [Show full text]
  • CALCULUS HANDOUT 6 - RIEMANN-DARBOUX INTEGRAL - Definitions
    CALCULUS HANDOUT 6 - RIEMANN-DARBOUX INTEGRAL - definitions THE RIEMANN DARBOUX INTEGRAL A partition P of the interval [a; b] is a finite set of points fx0; x1; ::; xng satisfying a = x0 < x1 < :: < xn = b. Consider a function f defined and bounded on [a; b]. n X Upper Darboux sum of f related to P : Uf (P ) = Mi(xi − xi−1) where Mi = sup f(x). i=1 xi−1≤x≤xi n X Lower Darboux sum of f related to P : Lf (P ) = mi(xi − xi−1) where mi = inf f(x). xi−1≤x≤xi i=1 Consider M = supff(x) j a ≤ x ≤ bg and m = infff(x) j a ≤ x ≤ bg. For any partition P of [a; b] we have: m(b − a) ≤ Lf (P ) ≤ Uf (P ) ≤ M(b − a). Lf = fLf (P ) j P is a partition of [a; b]g and Uf = fUf (P ) j P is a partition of [a; b]g are bounded sets. So Lf = sup Lf and Uf = inf Uf exist. Moreover, Lf ≤ Uf . A function defined and bounded on [a; b] is Riemann-Darboux integrable on [a; b] if Lf = Uf . Z b This common value is denoted by f(x) dx = Lf = Uf . a Properties of the Riemann-Darboux integral: If f and g are Riemann-Darboux integrable on [a; b] then all the integrals below exist and Z b Z b Z b (1) (α f(x) + β g(x)) dx = α f(x) dx + β g(x) dx for any α; β 2 R: a a a Z b Z c Z b (2) f(x) dx = f(x) dx + f(x) dx for any a ≤ c ≤ b.
    [Show full text]
  • Chapter 10 Multivariable Integral
    Chapter 10 Multivariable integral 10.1 Riemann integral over rectangles Note: ??? lectures As in chapter chapter 5, we define the Riemann integral using the Darboux upper and lower inte- grals. The ideas in this section are very similar to integration in one dimension. The complication is mostly notational. The differences between one and several dimensions will grow more pronounced in the sections following. 10.1.1 Rectangles and partitions Definition 10.1.1. Let (a ,a ,...,a ) and (b ,b ,...,b ) be such that a b for all k. A set of 1 2 n 1 2 n k ≤ k the form [a ,b ] [a ,b ] [a ,b ] is called a closed rectangle. In this setting it is sometimes 1 1 × 2 2 ×···× n n useful to allow a =b , in which case we think of [a ,b ] = a as usual. If a <b for all k, then k k k k { k} k k a set of the form(a 1,b 1) (a 2,b 2) (a n,b n) is called an open rectangle. × ×···× n For an open or closed rectangle R:= [a 1,b 1] [a 2,b 2] [a n,b n] R or R:= (a 1,b 1) n × ×···× ⊂ × (a2,b 2) (a n,b n) R , we define the n-dimensional volume by ×···× ⊂ V(R):= (b a )(b a ) (b a ). 1 − 1 2 − 2 ··· n − n A partition P of the closed rectangle R=[a ,b ] [a ,b ] [a ,b ] is afinite set of par- 1 1 × 2 2 ×···× n n titions P1,P2,...,Pn of the intervals [a1,b 1],[a 2,b 2],...,[a n,b n].
    [Show full text]
  • Profiles and Prospects*
    Indian Journal of History of Science, 47.3 (2012) 473-512 MATHEMATICS AND MATHEMATICAL RESEARCHES IN INDIA DURING FIFTH TO TWENTIETH CENTURIES — PROFILES AND PROSPECTS* A K BAG** (Received 1 September 2012) The Birth Centenary Celebration of Professor M. C. Chaki (1912- 2007), former First Asutosh Birth Centenary Professor of Higher Mathematics and a noted figure in the community of modern geometers, took place recently on 21 July 2012 in Kolkata. The year 2012 is also the 125th Birth Anniversary Year of great mathematical prodigy, Srinivas Ramanujan (1887-1920), and the Government of India has declared 2012 as the Year of Mathematics. To mark the occasion, Dr. A. K. Bag, FASc., one of the students of Professor Chaki was invited to deliver the Key Note Address. The present document made the basis of his address. Key words: Algebra, Analysis, Binomial expansion, Calculus, Differential equation, Fluid and solid mechanics, Function, ISI, Kerala Mathematics, Kut..taka, Mathemtical Modeling, Mathematical Societies - Calcutta, Madras and Allahabad, Numbers, Probability and Statistics, TIFR, Universities of Calcutta, Madras and Bombay, Vargaprakr.ti. India has been having a long tradition of mathematics. The contributions of Vedic and Jain mathematics are equally interesting. However, our discussion starts from 5th century onwards, so the important features of Indian mathematics are presented here in phases to make it simple. 500-1200 The period: 500-1200 is extremely interesting in the sense that this is known as the Golden (Siddha–ntic) period of Indian mathematics. It begins * The Key Note Address was delivered at the Indian Association for Cultivation of Science (Central Hall of IACS, Kolkata) organized on behalf of the M.C.
    [Show full text]
  • Riemann Integration
    Riemann integration Partition and integration of step functions • Integration theory is developed through the effort of making the ideas of “area” “volume” exact. Definition 1. (Partition) Let a, b ∈ R, a < b. A partition of the interval [ a, b] is a set of points P = { x0 , , xn } such that a = x0 < x1 < < xn = b. Definition 2. (Refinement) A refinement of a partition P is a partition Q ⊇ P. In this case we also say Q is finer than P. Definition 3. (Step function) A function f: [ a, b] R is called a step function if there is a partition P = { x0 , , xn } such that f( x) is constant on every ( x j − 1 , x j) . Remark 4. Note that there is some ambiguity in the definition as no restriction is put on the value of f at x0, , xn. Exercise 1. What is the reasonable value of “area below graph of f” for step functions? Then show that the values of f at x0, , xn do not matter as long as “area” is concerned. Darboux integral Definition 5. (Darboux sums and Darboux integrals) • For any fixed partition P, define the upper/lower sums as n n 7 U( f,P) 7 M ( f) ( x − x ); L( f,P) m ( f) ( x − x ) (1) X j j j − 1 X j j j − 1 j=1 j=1 where Mj( f) = max[ x j − 1 ,x j ] f( x) , mj( f) = min[ x j − 1 ,x j ] f( x) . • Now define the upper/lower integrals: U( f): =inf U( f,P); L( f): =sup L( f,P) .
    [Show full text]
  • On Some Perturbation Inequalities for Operators
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector On Some Perturbation Inequalities for Operators - Rajendra Bhatia Zndian Statistical Institute New Delhi-110016, India and Fuad Kittaneh Department of Mathematics Kuwait University Kuwait Submitted by Chandler Davis ABSTRACT An estimate for the norm of the solution to the equation AX - XB = S obtained by R. Bhatia, C. Davis, and A. McIntosh for normal operators A and B is shown to be valid for a larger class. Some other inequalities in the same spirit are obtained, including a “sin0 theorem” for singular vectors. Some inequalities concerning the continuity of the map A + IAl obtained recently by Kittaneh and Kosaki are extended using these ideas. Let H, and H, be any two Hilbert spaces, and let L(H,, H,) denote the space of bounded linear operators from H, to H,. Let L(H, H) be denoted simply as L(H). For A E L(H) let a(A) denote the spectrum of A. It has long been known (see [ll]) that if A and B are elements of L( H,) and L( H,), respectively, such that a( A) and a(B) are disjoint, then for every S in L(H,, H,) the equation AX - XB = S has a unique solution X E L(H,, H,). In their study of the subspace perturbation problem [4], R. Bhatia, C. Davis, and A. McIntosh obtained some estimates for the norm of X in terms of that of S and the number 6 = dist( a( A), u(B)).
    [Show full text]
  • Infosys Prize 2017
    Infosys Science Foundation INFOSYS PRIZE 2017 The Romanesco broccoli has fascinated photographers the world over. The brilliant chartreuse and the mesmerizing spiral spines belong to an edible flower bud of the species Brassica oleracea. Grown in Italy since the 16th century, this broccoli- cauliflower hybrid is nutritionally rich, with a delicate nutty flavor. Romanesco thus demands as much interest from chefs as from botanists and researchers. But it doesn’t stop there – peer closely and you will see just how incredible it really is. For it is one of the earth’s most stunning natural fractals. In other words, each of its buds is composed of a series of smaller buds, all arranged in yet another logarithmic spiral. The same pattern continues at several diminishing size levels. Studies of fractals found in nature, such as a snowflake or lightning bolts or indeed the Romanesco broccoli, trace a path to modern applications in computer graphics. We tend to divide and study distinct subjects – physics, biology, math, engineering and so on – only to find one interconnected universe. And it gets even more bizarre. The number of spirals on the head of a Romanesco broccoli is a natural approximation of the Fibonacci number. Named after the Italian mathematician, the Fibonacci spiral is a logarithmic spiral where every quarter turn is farther from the origin by a factor of phi, the golden ratio. How about that for a little bit of math in your soup? ENGINEERING AND COMPUTER SCIENCE The Infosys Prize 2017 in Engineering and Computer Science is awarded to Prof. Sanghamitra Bandyopadhyay for her scholarly record in algorithmic optimization and for its significant impact on biological data analysis.
    [Show full text]
  • MAT 320 Review Sheet for Final Exam with Solutions
    MAT 320 Foundations of Analysis Jason Starr Final Exam Spring 2015 Wednesday 5/13 5:30pm { 8:00pm MAT 320 Review Sheet for Final Exam with Solutions Remark. The Final Exam will be cumulative, although there will be an emphasis on material covered since Midterm 2. Please review Midterm 1 and Midterm 2. If you are comfortable with the material from Midterms 1 and 2, as well as the following, then you will be well prepared for the final exam. Exam Policies. You must show up on time for all exams. Please bring your student ID card: ID cards may be checked, and students may be asked to sign a picture sheet when turning in exams. Other policies for exams will be announced / repeated at the beginning of the exam. If you have a university-approved reason for taking an exam at a time different than the scheduled exam (because of a religious observance, a student-athlete event, etc.), please contact your instructor as soon as possible. Similarly, if you have a documented medical emergency which prevents you from showing up for an exam, again contact your instructor as soon as possible. All exams are closed notes and closed book. Once the exam has begun, having notes or books on the desk or in view will be considered cheating and will be referred to the Academic Judiciary. It is not permitted to use cell phones, calculators, laptops, MP3 players, Blackberries or other such electronic devices at any time during exams. If you use a hearing aid or other such device, you should make your instructor aware of this before the exam begins.
    [Show full text]