DOCSLIB.ORG

Lattices As Multidimensional Sampling Structures: Part I

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lattices As Multidimensional Sampling Structures: Part I Lattices as Multidimensional Sampling Structures: Part I Vishal Monga [email protected] September 20, 2007 1 Lattices De¯nition: A lattice ¤ in the N-dimensional real space RN , is the set of all linear combinations of N linearly independent real vectors v1;:::; vN of size N £ 1, which are known as the basis vectors of ¤, with integer coe±cients. ¤ can be written as the set ¤ = fVn j n 2 ZN g; (1) · ¸ . where Z denotes the set of all integers and V = v1 . ¢ ¢ ¢ . vN is a N £ N real-valued matrix, with the T basis vectors v1;:::; vN as its columns. For any point Vn in the lattice, the vector n = [n1; : : : ; nN ] is the representation of the point in the lattice with respect to V, which is often called the generating or the sampling matrix. For any lattice basis vectors are not unique. In fact, if EN£N is a matrix of integer numbers and det(E) = §1, then V^ = EV provides another set of basis vectors for ¤. De¯nition: Given a lattice ¤, one can ¯nd a unit cell U(¤) such that the entire RN space can be tiled by U(¤) and its translations to all lattice points. The unit cell associated with a lattice is not unique. However, two unit cells-namely Fundamental Parallelepiped and Voronoi Cell, are often encountered in the literature. 1. Fundamental parallelepiped: represents set of all points in RN within the region enclosed by the basis vectors and it can be expressed as the set ( ) XN N P(¤) = x 2 R j x = ®ivi; 8 0 · ®i · 1 : (2) i=1 1 y y 1 1 2 4 / w2 2 v2 x x v1 3 6 w1 1/3 2/3 3 3 2 1 3 0 V = / W = / 0 2 −1 4 1 2 / / (a) Basic lattice ¤ (b) Reciprocal lattice ¤¤ Figure 1: Example of a lattice in two dimensions. 2. Voronoi cell: represents the set of all points in RN closer to origin 0 than to any of the lattice points and it can be expressed as © ª V(¤) = x 2 RN j d(x; 0) · d(x; p); 8 p 2 ¤ ; (3) where d(a; b) is the Euclidean distance between the points a and b. Examples of these unit cells for a lattice whose generator matrix is V is shown in Fig. 1(a). y y P(Λ) V(Λ) x x (a) Fundamental parallelepiped (b) Voronoi cell Figure 2: Unit cells for the lattice of Fig 1(a). Although a unit cell for a lattice is not unique, hyper-volume of the unit cell of a lattice denoted by d(¤) = det(V) is unique. Another useful term associated with the lattices is Sampling density, which is computed as 1 Sampling density = : (4) d(¤) 2 De¯nition: Let ¤ and ¡ be two lattices. ¤ is a sublattice of ¡, if every point in ¤ is also a point in ¡. The ratio d(¤)=d(¡) is called the index of ¤ in ¡. The set c + ¤ = fc + x j x 2 ¤g for any c 2 ¡ is called a coset or class of ¤ in ¡. Two cosets c + ¤ and d + ¤ are identical if and only if c ¡ d 2 ¤. De¯nition: Given a lattice ¤, the set of all vectors y such that yT x 2 Z; 8x 2 ¤ is called the reciprocal (polar) lattice of ¤ and it can be represented as the set: © ª ¤¤ = Wn = V¡T n j n 2 ZN : (5) T It can be seen that W V = IN£N and 1 d (¤¤) = : (6) d (¤) Thus, denser ¤ ensures a sparser ¤¤ and vice versa. An example for a reciprocal lattice is shown in Fig. 1(b) for the lattice shown in Fig. 1(a). Theorem: Let ¤1 and ¤2 be two lattices of dimension N. Intersection of these lattices ¤1 \ ¤2 is also a lattice, however its dimension could be less than or equal to N. A necessary and su±cient condition for ¤1 \¤2 ¡1 N£N to be N-dimensional, is that V1 V2 2 Q , where Q is the set of rational numbers. ¤1 \ ¤2 is the largest lattice that is contained in both ¤1 and ¤2. Similarly, ¤1 + ¤2 = fx + y j 8 x 2 ¤1; 8 y 2 ¤2g (7) is the smallest lattice that contains both ¤1 and ¤2. Furthermore, ¤ ¤ ¤ (¤1 + ¤2) = ¤1 \ ¤2 and (8) ¤ ¤ ¤ (¤1 \ ¤2) = ¤1 + ¤2: (9) Thus, if an algorithm is present to ¯nd the intersection of lattices; it can be used to ¯nd sum of lattices as well. 3 2 Sampling Over Lattices De¯nition: A function Ã(x) is periodic with a non-singular periodicity matrix V if Ã(x) = Ã(x + Vn) 8n 2 ZN . When a lattice is used to describe the periodicity of a function, it is usually referred as the periodicity lattice and a unit cell of the lattice is referred as the fundamental period of the function. N De¯nition: Given a continuous signal sc(x); x 2 R , a sampled signal over a lattice ¤ with a generating matrix V is de¯ned as: X N s(x) = sc(x)± (x ¡ Vn) ; x 2 R : (10) n2ZN 2.1 Fourier Transform of Signals Sampled on Lattices X X S(u) = s(x) exp(¡2¼juT x) = s(Vn) exp(2¼juT Vn); (11) x2¤ n2ZN T where u = [u1; u2; : : : ; uN ] represents the frequency coordinates. Let r be a point in ¤¤. S(u + r) can be written as: X S(u + r) = S(Vn) exp(¡2¼j(u + r)T Vn) (12) n2ZN X = S(Vn) exp(¡2¼juT Vn) exp(¡2¼jrT Vn): (13) n2ZN From the de¯nition of the reciprocal lattice rT x is an integer 8 x 2 ¤; r 2 ¤¤. Thus, Fourier transform is periodic with W = V¡T the generator matrix for the reciprocal lattice of ¤. Similarly, the inverse Fourier transform can be computed as: Z s(x) = d(¤) S(u) exp(2¼juT x)du); x 2 ¤: (14) U(¤¤) 2.2 Sampling on Cosets Let ª be discrete set of points in RN such that it is a union of distinct cosets of a sublattice ¤ in a lattice ¡. Thus, we have [P ª = (ci + ¤); (15) i=1 4 where ci is a vector in ¡. Sampled signal can be written as X T s(u) = sc(x) exp(¡2¼ju x) (16) x2ª and its Fourier transform can accordingly be written as XP X T S(u) = s(ci + x) exp(¡2¼ju (ci + x)) (17) i x2¤ XP X T T = exp(¡2¼ju ci) s(ci + x) exp(¡2¼ju x) (18) i=1 x2¤ XP T = exp(¡2¼ju ci)Si(u); (19) i=1 whose periodicity is determined by the lattice ¡¤. 2.3 Generalized Nyquist Sampling Theorem 1 X S(u) = S (u ¡ r); (20) d(¤) c r2¤¤ where Sc(u) is the continuous Fourier transform of sc(x). It is possible to recover the original continuous signal from the sampled signal perfectly if and only if the support ¤ region of Sc(u) is limited within the fundamental period of the reciprocal lattice ¤ . Use the reconstruction ¯lter ½ d(¤); u 2 U(¤¤) H (u) = (21) r 0; o:w: to interpolate between the samples. In order to avoid aliasing, use the ¯lter ½ 1; u 2 U(¤¤) H (u) = (22) AA 0; o:w: ¤ and to recover the original signal perfectly, U(¤ ) should be at least 2 £ BW(Sc(u)), where BW(Sc(u)) is the support region of the continuous signal. 2.4 Sampling E±ciency By using very high sampling density, it can be ensured U(¤¤) covers the support of the continuous time signal. However, at the same time, it is desired that the number of samples that is enough to reconstruct the original signal is the smallest. This can be achieved if U(¤¤) covers the support of the continuous signal as tightly as possible. 5 De¯nition: For a circularly bandlimited signal, the ratio of the hyper-volume of the hyper-sphere that de¯nes the bandwidth of the signal to the hyper-volume of the smallest U(¤¤) that covers this hyper-sphere is called the sampling e±ciency of the sampling structure. V (1) ½(¤) = N ; (23) d(¤¤) where VN (1) is the hyper-volume of the unit hyper-sphere in N dimensions. In Fig. 2.4, sampling e±ciencies of 3 di®erent geometries is shown. As a matter of fact, it can be shown for a r =1 r =1 r =1 Λ Λ Λ d( ∗)=4 d( ∗)=4 d( ∗)=2√3 ρ(Λ)= π 0.785 ρ(Λ)= π 0.785 ρ(Λ)= π 0.907 4 ≈ 4 ≈ 2√3 ≈ Figure 3: Sampling e±ciencies of di®erent geometries. circularly bandlimited signal hexagonal sampling lattice has the highest e±ciency among the others. In Table. 1, the sampling e±ciency of a rectangular lattice is compared against a hexagonal lattice. M ´ = ½(¤R) ½(¤H ) 1 1.000 2 0.866 3 0.705 5 0.353 8 0.062 Table 1: Rectangular vs. Hexagonal sampling e±ciency It can be seen that for 1-D signals, there is no di®erence between the structures. However, as N increases the e±cacy of hexagonal sampling is obvious. For example, for a continuous 2-D signal, hexagonal lattice can reconstruct the signal with approximately 13:4% less samples than a rectangular lattice requires. 6 3 Sampling Rate Conversion Let s(x) is the sampled version of a continuous signal sc(x) on a lattice ¤1, we would like to obtain s(y) which is the sampled version of sc(x) on a lattice ¤2 by using s(x).
Load more

Recommended publications
  • Designing Commutative Cascades of Multidimensional Upsamplers And
    IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 0 Designing Commutative Cascades of Multidimensional Upsamplers and Downsamplers Brian L. Evans, Member, IEEE Abstract In multiple dimensions, the cascade of an upsampler by L and a downsampler by L commutes if and only if the integer matrices L and M are right coprime and LM = ML. This pap er presents algorithms to design L and M that yield commutative upsampler/dowsampler cascades. We prove that commutativity is p ossible if the 1 Jordan canonical form of the rational resampling matrix R = LM is equivalent to the Smith-McMillan form of R. A necessary condition for this equivalence is that R has an eigendecomp osition and the eigenvalues are rational. B. L. Evans is with the Department of Electrical and Computer Engineering, The UniversityofTexas at Austin, Austin, TX 78712-1084, USA. E-mail: [email protected], Web: http://www.ece.utexas.edu/~b evans, Phone: 512 232-1457, Fax: 512 471-5907. This work was sp onsored in part by NSF CAREER Award under Grant MIP-9702707. July 31, 1997 DRAFT IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 1 I. Introduction 1 Resampling systems scale the sampling rate by a rational factor R = L=M = LM , or 1 equivalently decimate by H = M=L = L M [1], by essentially upsampling by L, ltering, and downsampling by M . In converting compact disc data sampled at 44.1 kHz to digital audio tap e 48000 Hz 160 data sampled at 48 kHz, R = = . Because we can always factor R into coprime 44100 Hz 147 integers L and M , we can always commute the upsampler and downsampler which leads to ecient p olyphase structures of the resampling system.
    [Show full text]
  • Hexagonal Structure for Intelligent Vision
    © 2005 IEEE. Reprinted, with permission, from Xiangjian He, Hexagonal Structure for Intelligent Vision . Information and Communication Technologies, 2005. ICICT 2005. First International Conference on, August 2005. This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE endorsement of any of the University of Technology, Sydney's products or services. Internal or personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution must be obtained from the IEEE by writing to pubs- [email protected]. By choosing to view this document, you agree to all provisions of the copyright laws protecting it HEXAGONAL STRUCTURE FOR INTELLIGENT VISION Xiangjian He and Wenjing Jia Computer Vision Research Group Faculty of Information Technology University of Technology, Sydney Australia Abstract: greater angular resolution, and a reduced need of storage Using hexagonal grids to represent digital images has and computation in image processing operations. been studied for more than 40 years. Increased processing In spite of its numerous advantages, hexagonal grid has so capabilities of graphic devices and recent improvements in far not yet been widely used in computer vision and CCD technology have made hexagonal sampling graphics field. The main problem that limits the use of attractive for practical applications and brought new hexagonal image structure is believed due to lack of interests on this topic. The hexagonal structure is hardware for capturing and displaying hexagonal-based considered to be preferable to the rectangular structure images.
    [Show full text]
  • Deep Image Prior for Undersampling High-Speed Photoacoustic Microscopy
    Photoacoustics 22 (2021) 100266 Contents lists available at ScienceDirect Photoacoustics journal homepage: www.elsevier.com/locate/pacs Deep image prior for undersampling high-speed photoacoustic microscopy Tri Vu a,*, Anthony DiSpirito III a, Daiwei Li a, Zixuan Wang c, Xiaoyi Zhu a, Maomao Chen a, Laiming Jiang d, Dong Zhang b, Jianwen Luo b, Yu Shrike Zhang c, Qifa Zhou d, Roarke Horstmeyer e, Junjie Yao a a Photoacoustic Imaging Lab, Duke University, Durham, NC, 27708, USA b Department of Biomedical Engineering, Tsinghua University, Beijing, 100084, China c Division of Engineering in Medicine, Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Cambridge, MA, 02139, USA d Department of Biomedical Engineering and USC Roski Eye Institute, University of Southern California, Los Angeles, CA, 90089, USA e Computational Optics Lab, Duke University, Durham, NC, 27708, USA ARTICLE INFO ABSTRACT Keywords: Photoacoustic microscopy (PAM) is an emerging imaging method combining light and sound. However, limited Convolutional neural network by the laser’s repetition rate, state-of-the-art high-speed PAM technology often sacrificesspatial sampling density Deep image prior (i.e., undersampling) for increased imaging speed over a large field-of-view. Deep learning (DL) methods have Deep learning recently been used to improve sparsely sampled PAM images; however, these methods often require time- High-speed imaging consuming pre-training and large training dataset with ground truth. Here, we propose the use of deep image Photoacoustic microscopy Raster scanning prior (DIP) to improve the image quality of undersampled PAM images. Unlike other DL approaches, DIP requires Undersampling neither pre-training nor fully-sampled ground truth, enabling its flexible and fast implementation on various imaging targets.
    [Show full text]
  • ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform
    Department of Electrical Engineering University of Arkansas ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform Dr. Jingxian Wu [email protected] 2 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • DTFT of Sampled Signals • Upsampling and downsampling 3 DTFT • Discrete-time Fourier Transform (DTFT) X () x(n)e jn n – (radians): digital frequency • Review: Z-transform: X (z) x(n)zn n0 j X () X (z) | j – Replace z with e . ze • Review: Fourier transform: X () x(t)e jt – (rads/sec): analog frequency 4 DTFT • Relationship between DTFT and Fourier Transform – Sample a continuous time signal x a ( t ) with a sampling period T xs (t) xa (t) (t nT ) xa (nT ) (t nT ) n n – The Fourier Transform of ys (t) jt jnT X s () xs (t)e dt xa (nT)e n – Define: T • : digital frequency (unit: radians) • : analog frequency (unit: radians/sec) – Let x(n) xa (nT) X () X s T 5 DTFT • Relationship between DTFT and Fourier Transform (Cont’d) – The DTFT can be considered as the scaled version of the Fourier transform of the sampled continuous-time signal jt jnT X s () xs (t)e dt xa (nT)e n x(n) x (nT) T a jn X () X s x(n)e T n 6 DTFT • Discrete Frequency – Unit: radians (the unit of continuous frequency is radians/sec) – X ( ) is a periodic function with period 2 j2 n jn j2n jn X ( 2 ) x(n)e x(n)e e x(n)e X () n n n – We only need to consider for • For Fourier transform, we need to consider 1 – f T 2 2T 1 – f T 2 2T 7 DTFT • Example: find the DTFT of the following signal – 1.
    [Show full text]
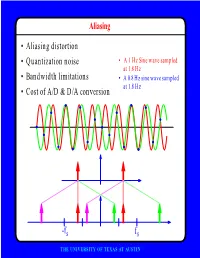
  • F • Aliasing Distortion • Quantization Noise • Bandwidth Limitations • Cost of A/D & D/A Conversion
    Aliasing • Aliasing distortion • Quantization noise • A 1 Hz Sine wave sampled at 1.8 Hz • Bandwidth limitations • A 0.8 Hz sine wave sampled at 1.8 Hz • Cost of A/D & D/A conversion -fs fs THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Perfect reconstruction of a Better trade-off between signal is possible even after bandwidth and noise severe distortion immunity performance digital analog bandwidth Increase signal-to-noise ratio simply by adding more bits SNR = -7.2 + 6 dB/bit THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Programmability • Modifiable in the field • Implement multiple standards • Better user interfaces • Tolerance for changes in specifications • Get better use of hardware for low-speed operations • Debugging • User programmability THE UNIVERSITY OF TEXAS AT AUSTIN Disadvantages of Digital Systems Programmability • Speed is too slow for some applications • High average power and peak power consumption RISC (2 Watts) vs. DSP (50 mW) DATA PROG MEMORY MEMORY HARVARD ARCHITECTURE • Aliasing from undersampling • Clipping from quantization Q[v] v v THE UNIVERSITY OF TEXAS AT AUSTIN Analog-to-Digital Conversion 1 --- T h(t) Q[.] xt() yt() ynT() yˆ()nT Anti-Aliasing Sampler Quantizer Filter xt() y(nT) t n y(t) ^y(nT) t n THE UNIVERSITY OF TEXAS AT AUSTIN Resampling Changing the Sampling Rate • Conversion between audio formats Compact 48.0 Digital Disc ---------- Audio Tape 44.1 KHz44.1 48 KHz • Speech compression Speech 1 Speech for on DAT --- Telephone 48 KHz 6 8 KHz • Video format conversion
    [Show full text]
  • Multidimensional Sampling Dr
    Multidimensional Sampling Dr. Vishal Monga Motivation for the General Case for Sampling We need the more general case to treat three important applications. 1. Human Vision System: the human vision system is a nonlinear, spatially- varying, non-uniformly sampled system. Rods and cones on the retina, which spatially sample are not arranged in rows and columns. a. Hexagonal Sampling: when modeled as a linear shift-invariant system, the human visual system is circularly bandlimited (lowpass in radial frequency). The optimal uniform sampling grid is hexagonal. Optimal means that we need the fewest discrete-time samples to sample the continuous-space analog signal without aliasing. b. Foveated grid: This is based on the fovea in the retina. When you focus on an object, you sample the object at a high resolution, and the resolution falls off away from the point-of-focus. Shown below is a simple example of a foveated grid. The grid is a 4 x 4 uniform sampling with each of the middle four grids subdivided into 4 x 4 grids themselves. The point of focus is at the middle of the grid. We can convert this grid to a uniform grid in several ways. For example, we could start with a rectangular grid and keep the resolution at the point-of-focus. Then, away from the point-of-focus, we can average the pixel values in increasingly larger blocks of samples. This approach allows the use a foveated grid while maintaining compatibility with systems that require rectangular sampling (e.g. image and video compression standards). 2. Television 650 samples /row 362.5 rows /interlace 2 interlaces /frame 30 frames /sec No two samples taken at the same instant of time Can signals be sampled this way without losing information? How can we handle a.
    [Show full text]
  • ARRAY SET ADDRESSING: ENABLING EFFICIENT HEXAGONALLY SAMPLED IMAGE PROCESSING by NICHOLAS I. RUMMELT a DISSERTATION PRESENTED TO
    ARRAY SET ADDRESSING: ENABLING EFFICIENT HEXAGONALLY SAMPLED IMAGE PROCESSING By NICHOLAS I. RUMMELT A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY UNIVERSITY OF FLORIDA 2010 1 °c 2010 Nicholas I. Rummelt 2 To my beautiful wife and our three wonderful children 3 ACKNOWLEDGMENTS Thanks go out to my family for their support, understanding, and encouragement. I especially want to thank my advisor and committee chair, Joseph N. Wilson, for his keen insight, encouragement, and excellent guidance. I would also like to thank the other members of my committee: Paul Gader, Arunava Banerjee, Jeffery Ho, and Warren Dixon. I would like to thank the Air Force Research Laboratory (AFRL) for generously providing the opportunity, time, and funding. There are many people at AFRL that played some role in my success in this endeavor to whom I owe a debt of gratitude. I would like to specifically thank T.J. Klausutis, Ric Wehling, James Moore, Buddy Goldsmith, Clark Furlong, David Gray, Paul McCarley, Jimmy Touma, Tony Thompson, Marta Fackler, Mike Miller, Rob Murphy, John Pletcher, and Bob Sierakowski. 4 TABLE OF CONTENTS page ACKNOWLEDGMENTS .................................. 4 LIST OF TABLES ...................................... 7 LIST OF FIGURES ..................................... 8 ABSTRACT ......................................... 10 CHAPTER 1 INTRODUCTION AND BACKGROUND ...................... 11 1.1 Introduction ................................... 11 1.2 Background ................................... 11 1.3 Recent Related Research ........................... 15 1.4 Recent Related Academic Research ..................... 16 1.5 Hexagonal Image Formation and Display Considerations ......... 17 1.5.1 Converting from Rectangularly Sampled Images .......... 17 1.5.2 Hexagonal Imagers ..........................
    [Show full text]
  • Hexagonal QMF Banks and Wavelets
    Hexagonal QMF Banks and Wavelets A chapter within Time-Frequency and Wavelet Transforms in Biomedical Engineering, M. Akay (Editor), New York, NY: IEEE Press, 1997. Sergio Schuler and Andrew Laine Computer and Information Science and Engineering Department UniversityofFlorida Gainesville, FL 32611 2 Hexagonal QMF Banks and Wavelets Sergio Schuler and Andrew Laine Department of Computer and Information Science and Engineering University of Florida Gainesville, FL 32611 Introduction In this chapter weshalllay bare the theory and implementation details of hexagonal sampling systems and hexagonal quadrature mirror lters (HQMF). Hexagonal sampling systems are of particular interest b ecause they exhibit the tightest packing of all regular two-dimensional sampling systems and for a circularly band-limited waveform, hexagonal sampling requires 13.4 p ercentfewer samples than rectangular sampling [1]. In addition, hexagonal sampling systems also lead to nonseparable quadrature mirror lters in which all basis functions are lo calized in space, spatial frequency and orientation [2]. This chapter is organized in two sections. Section I describ es the theoretical asp ects of hexagonal sampling systems while Section I I covers imp ortant implementation details. I. Hexagonal sampling system This section presents the theoretical foundation of hexagonal sampling systems and hexagonal quadrature mirror lters. Most of this material has app eared elsewhere in [1], [3], [4], [5], [2], [6] but is describ ed here under a uni ed notation for completeness. In addition, it will provide continuity and a foundation for the original material that follows in Section I I. The rest of the section is organized as follows. Section I-A covers the general formulation of a hexagonal sampling system.
    [Show full text]
  • JASON Manual
    Weiss Engineering Ltd. Florastrasse 42, 8610 Uster, Switzerland www.weiss-highend.com JASON OWNERS MANUAL OWNERS MANUAL FOR WEISS JASON CD TRANSPORT INTRODUCTION Dear Customer Congratulations on your purchase of the JASON CD Transport and welcome to the family of Weiss equipment owners! The JASON is the result of an intensive research and development process. Research was conducted both in analog and digital circuit design, as well as in signal processing algorithm specification. On the following pages I will introduce you to our views on high quality audio processing. These include fundamental digital and analog audio concepts and the JASON CD Transport. I wish you a long-lasting relationship with your JASON. Yours sincerely, Daniel Weiss President, Weiss Engineering Ltd. Page: 2 Date: 03/13 /dw OWNERS MANUAL FOR WEISS JASON CD TRANSPORT TABLE OF CONTENTS 4 A short history of Weiss Engineering 5 Our mission and product philosophy 6 Advanced digital and analog audio concepts explained 6 Jitter Suppression, Clocking 8 Upsampling, Oversampling and Sampling Rate Conversion in General 11 Reconstruction Filters 12 Analog Output Stages 12 Dithering 14 The JASON CD Transport 14 Features 17 Operation 21 Technical Data 22 Contact Page: 3 Date: 03/13 /dw OWNERS MANUAL FOR WEISS JASON CD TRANSPORT A SHORT HISTORY OF WEISS ENGINEERING After studying electrical engineering, Daniel Weiss joined the Willi Studer (Studer - Revox) company in Switzerland. His work included the design of a sampling frequency converter and of digital signal processing electronics for digital audio recorders. In 1985, Mr. Weiss founded the company Weiss Engineering Ltd. From the outset the company concentrated on the design and manufacture of digital audio equipment for mastering studios.
    [Show full text]
  • MULTIRATE SIGNAL PROCESSING Multirate Signal Processing
    MULTIRATE SIGNAL PROCESSING Multirate Signal Processing • Definition: Signal processing which uses more than one sampling rate to perform operations • Upsampling increases the sampling rate • Downsampling reduces the sampling rate • Reference: Digital Signal Processing, DeFatta, Lucas, and Hodgkiss B. Baas, EEC 281 431 Multirate Signal Processing • Advantages of lower sample rates –May require less processing –Likely to reduce power dissipation, P = CV2 f, where f is frequently directly proportional to the sample rate –Likely to require less storage • Advantages of higher sample rates –May simplify computation –May simplify surrounding analog and RF circuitry • Remember that information up to a frequency f requires a sampling rate of at least 2f. This is the Nyquist sampling rate. –Or we can equivalently say the Nyquist sampling rate is ½ the sampling frequency, fs B. Baas, EEC 281 432 Upsampling Upsampling or Interpolation •For an upsampling by a factor of I, add I‐1 zeros between samples in the original sequence •An upsampling by a factor I is commonly written I For example, upsampling by two: 2 • Obviously the number of samples will approximately double after 2 •Note that if the sampling frequency doubles after an upsampling by two, that t the original sample sequence will occur at the same points in time t B. Baas, EEC 281 434 Original Signal Spectrum •Example signal with most energy near DC •Notice 5 spectral “bumps” between large signal “bumps” B. Baas, EEC 281 π 2π435 Upsampled Signal (Time) •One zero is inserted between the original samples for 2x upsampling B. Baas, EEC 281 436 Upsampled Signal Spectrum (Frequency) • Spectrum of 2x upsampled signal •Notice the location of the (now somewhat compressed) five “bumps” on each side of π B.
    [Show full text]
  • Discrete Generalizations of the Nyquist-Shannon Sampling Theorem
    DISCRETE SAMPLING: DISCRETE GENERALIZATIONS OF THE NYQUIST-SHANNON SAMPLING THEOREM A DISSERTATION SUBMITTED TO THE DEPARTMENT OF ELECTRICAL ENGINEERING AND THE COMMITTEE ON GRADUATE STUDIES OF STANFORD UNIVERSITY IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY William Wu June 2010 © 2010 by William David Wu. All Rights Reserved. Re-distributed by Stanford University under license with the author. This work is licensed under a Creative Commons Attribution- Noncommercial 3.0 United States License. http://creativecommons.org/licenses/by-nc/3.0/us/ This dissertation is online at: http://purl.stanford.edu/rj968hd9244 ii I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. Brad Osgood, Primary Adviser I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. Thomas Cover I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. John Gill, III Approved for the Stanford University Committee on Graduate Studies. Patricia J. Gumport, Vice Provost Graduate Education This signature page was generated electronically upon submission of this dissertation in electronic format. An original signed hard copy of the signature page is on file in University Archives. iii Abstract 80, 0< 11 17 æ 80, 1< 5 81, 0< 81, 1< 12 83, 1< 84, 0< 82, 1< 83, 4< 82, 3< 15 7 6 83, 2< 83, 3< 84, 8< 83, 6< 83, 7< 13 3 æ æ æ æ æ æ æ æ æ æ 9 -5 -4 -3 -2 -1 1 2 3 4 5 84, 4< 84, 13< 84, 14< 1 HIS DISSERTATION lays a foundation for the theory of reconstructing signals from T finite-dimensional vector spaces using a minimal number of samples.
    [Show full text]
  • DCT Coding of Nonrectangularly Sampled Images Emre Giinduzhan, A
    IEEE SIGNAL PROCESSING LETTERS, VOL. 1, NO. 9, SEPTEMBER 1994 131 DCT Coding of Nonrectangularly Sampled Images Emre Giinduzhan, A. Enis Cetin, and A Murat Tekalp ... Abstmct-Discrete cosine transform (DCT) coding is widely used for compression of re.ctangularly sampled images. In this .... ................ letter, we address efficient DCT coding of "rectangularly sam- ... ....... pled images. To eKect, we discuss efecient method for .......... this an -....__ -._. the computation of the DCT on nomctanpb sampling grids .. ..........~--__ using the Smith-normal &"position. Sim- results are provided. .... .......... I. INTRODUCTION ...I.. ...... ... N DIGITAL representation of multidimensional (M-D) .... Isignals, various sampling structures can be used that are usually in the form of a lattice or a union of coset of a N=[; :]=[2-1]r-110312 '1 lattice [ 11. Rectangular sampling grids (orthogonal lattices) are the most commonly used lattice smcture. It is well Fig. 1. Coordinate transformation in a hexagonal lattice. known that the sampling efficiency of e depends on the region of support of the spectrum malog signal [2]r [3]. In still images, a 2-D nonreckuguhr sampling grid is first transformed onto a new coordinate system, where it is may require. a smaller number of sampks'per unit area than rectangularly periodic. Rectangular M-D DCT of the trans- a rectangular grid. In video, interlaced sampling grids (3-D formed sequence is computed in the new coordinates, and the nonrectangular @ids) are widely used for reduced flickering result is transformed back to the original coordinates. A short without increasing the transmission bandwidth. review of the notation and the Smith-normal decomposition Most algorithm currently used for processing and compres- is given in Section 11.
    [Show full text]