Transit Timing and Duration Variations for the Discovery and Characterization of Exoplanets
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HD 97658 and Its Super-Earth Spitzer & MOST Transit Analysis and Seismic Modeling of the Host Star
The space photometry revolution CoRoT3-KASC7 joint meeting HD 97658 and its super-Earth Spitzer & MOST transit analysis and seismic modeling of the host star Valerie Van Grootel (University of Liege, Belgium) M. Gillon (U. Liege), D. Valencia (U. Toronto), N. Madhusudhan (U. Cambridge), D. Dragomir (UC Santa Barbara), and the Spitzer team 1. Introducing HD 97658 and its super-Earth The second brightest star harboring a transiting super-Earth HD 97658 (V=7.7, K=5.7) HD 97658 b, a transiting super-Earth • • Teff = 5170 ± 50 K (Howard et al. 2011) Discovery by Howard et al. (2011) from Keck- Hires RVs: • [Fe/H] = -0.23 ± 0.03 ~ Z - M sin i = 8.2 ± 1.2 M • d = 21.11 ± 0.33 pc ; from Hipparcos P earth - P = 9.494 ± 0.005 d (Van Leeuwen 2007) orb • Transits discovered by Dragomir et al. (2013) with MOST: RP = 2.34 ± 0.18 Rearth From Howard et al. (2011) From Dragomir et al. (2013) Valerie Van Grootel – CoRoT/Kepler July 2014, Toulouse 2 2. Modeling the host star HD 97658 Rp α R* 2/3 Mp α M* Radial velocities Transits + the age of the star is the best proxy for the age of its planets (Sun: 4.57 Gyr, Earth: 4.54 Gyr) • With Asteroseismology: T. Campante, V. Van Eylen’s talks • Without Asteroseismology: stellar evolution modeling Valerie Van Grootel – CoRoT/Kepler July 2014, Toulouse 3 2. Modeling the host star HD 97658 • d = 21.11 ± 0.33 pc, V = 7.7 L* = 0.355 ± 0.018 Lsun • +Teff from spectroscopy: R* = 0.74 ± 0.03 Rsun • Stellar evolution code CLES (Scuflaire et al. -

Circumbinary Habitable Zones in the Presence of a Giant Planet
Circumbinary habitable zones in the presence of a giant planet Nikolaos Georgakarakos 1;2;∗, Siegfried Eggl 4;5;6;7 and Ian Dobbs-Dixon 1;2;3 1 Division of Science, New York University Abu Dhabi, Abu Dhabi, UAE 2Center for Astro, Particle and Planetary Physics (CAP3), New York University Abu Dhabi,UAE 3Center for Space Sciences, New York University Abu Dhabi,UAE 4Department of Astronomy, University of Washington, Seattle, WA, USA 5Vera C. Rubin Observatory, Tucson, Arizona, USA 6Department of Aerospace Engineering, University of Chicago at Urbana-Champaign, Urbana, IL, USA 7IMCCE, Observatoire de Paris, Paris, France Correspondence*: Nikolaos Georgakarakos [email protected] ABSTRACT Determining habitable zones in binary star systems can be a challenging task due to the combination of perturbed planetary orbits and varying stellar irradiation conditions. The concept of “dynamically informed habitable zones” allows us, nevertheless, to make predictions on where to look for habitable worlds in such complex environments. Dynamically informed habitable zones have been used in the past to investigate the habitability of circumstellar planets in binary systems and Earth-like analogs in systems with giant planets. Here, we extend the concept to potentially habitable worlds on circumbinary orbits. We show that habitable zone borders can be found analytically even when another giant planet is present in the system. By applying this methodology to Kepler-16, Kepler-34, Kepler-35, Kepler-38, Kepler-64, Kepler-413, Kepler-453, Kepler-1647 and Kepler-1661 we demonstrate that the presence of the known giant planets in the majority of those systems does not preclude the existence of potentially habitable worlds. -

The NTT Provides the Deepest Look Into Space 6
The NTT Provides the Deepest Look Into Space 6. A. PETERSON, Mount Stromlo Observatory,Australian National University, Canberra S. D'ODORICO, M. TARENGHI and E. J. WAMPLER, ESO The ESO New Technology Telescope r on La Silla has again proven its extraor- - dinary abilities. It has now produced the "deepest" view into the distant regions of the Universe ever obtained with ground- or space-based telescopes. Figure 1 : This picture is a reproduction of a I.1 x 1.1 arcmin portion of a composite im- age of forty-one 10-minute exposures in the V band of a field at high galactic latitude in the constellation of Sextans (R.A. loh 45'7 Decl. -0' 143. The individual images were obtained with the EMMI imager/spectrograph at the Nas- myth focus of the ESO 3.5-m New Technolo- gy Telescope using a 1000 x 1000 pixel Thomson CCD. This combination gave a full field of 7.6 x 7.6 arcmin and a pixel size of 0.44 arcsec. The average seeing during these exposures was 1.0 arcsec. The telescope was offset between the indi- vidual exposures so that the sky background could be used to flat-field the frame. This procedure also removed the effects of cos- mic rays and blemishes in the CCD. More than 97% of the objects seen in this sub- field are galaxies. For the brighter galax- ies, there is good agreement between the galaxy counts of Tyson (1988, Astron. J., 96, 1) and the NTT counts for the brighter galax- ies. -

Planet Hunters. VI: an Independent Characterization of KOI-351 and Several Long Period Planet Candidates from the Kepler Archival Data
Accepted to AJ Planet Hunters VI: An Independent Characterization of KOI-351 and Several Long Period Planet Candidates from the Kepler Archival Data1 Joseph R. Schmitt2, Ji Wang2, Debra A. Fischer2, Kian J. Jek7, John C. Moriarty2, Tabetha S. Boyajian2, Megan E. Schwamb3, Chris Lintott4;5, Stuart Lynn5, Arfon M. Smith5, Michael Parrish5, Kevin Schawinski6, Robert Simpson4, Daryll LaCourse7, Mark R. Omohundro7, Troy Winarski7, Samuel Jon Goodman7, Tony Jebson7, Hans Martin Schwengeler7, David A. Paterson7, Johann Sejpka7, Ivan Terentev7, Tom Jacobs7, Nawar Alsaadi7, Robert C. Bailey7, Tony Ginman7, Pete Granado7, Kristoffer Vonstad Guttormsen7, Franco Mallia7, Alfred L. Papillon7, Franco Rossi7, and Miguel Socolovsky7 [email protected] ABSTRACT We report the discovery of 14 new transiting planet candidates in the Kepler field from the Planet Hunters citizen science program. None of these candidates overlapped with Kepler Objects of Interest (KOIs) at the time of submission. We report the discovery of one more addition to the six planet candidate system around KOI-351, making it the only seven planet candidate system from Kepler. Additionally, KOI-351 bears some resemblance to our own solar system, with the inner five planets ranging from Earth to mini-Neptune radii and the outer planets being gas giants; however, this system is very compact, with all seven planet candidates orbiting . 1 AU from their host star. A Hill stability test and an orbital integration of the system shows that the system is stable. Furthermore, we significantly add to the population of long period 1This publication has been made possible through the work of more than 280,000 volunteers in the Planet Hunters project, whose contributions are individually acknowledged at http://www.planethunters.org/authors. -

Epo in a Multinational Context
→EPO IN A MULTINATIONAL CONTEXT Heidelberg, June 2013 ESA FACTS AND FIGURES • Over 40 years of experience • 20 Member States • Six establishments in Europe, about 2200 staff • 4 billion Euro budget (2013) • Over 70 satellites designed, tested and operated in flight • 17 scientific satellites in operation • Six types of launcher developed • Celebrated the 200th launch of Ariane in February 2011 2 ACTIVITIES ESA is one of the few space agencies in the world to combine responsibility in nearly all areas of space activity. • Space science • Navigation • Human spaceflight • Telecommunications • Exploration • Technology • Earth observation • Operations • Launchers 3 →SCIENCE & ROBOTIC EXPLORATION TODAY’S SCIENCE MISSIONS (1) • XMM-Newton (1999– ) X-ray telescope • Cluster (2000– ) four spacecraft studying the solar wind • Integral (2002– ) observing objects in gamma and X-rays • Hubble (1990– ) orbiting observatory for ultraviolet, visible and infrared astronomy (with NASA) • SOHO (1995– ) studying our Sun and its environment (with NASA) 5 TODAY’S SCIENCE MISSIONS (2) • Mars Express (2003– ) studying Mars, its moons and atmosphere from orbit • Rosetta (2004– ) the first long-term mission to study and land on a comet • Venus Express (2005– ) studying Venus and its atmosphere from orbit • Herschel (2009– ) far-infrared and submillimetre wavelength observatory • Planck (2009– ) studying relic radiation from the Big Bang 6 UPCOMING MISSIONS (1) • Gaia (2013) mapping a thousand million stars in our galaxy • LISA Pathfinder (2015) testing technologies -
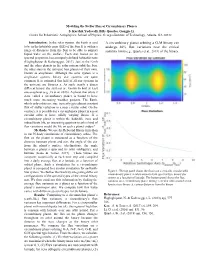
Is Near 0.3, (2) Flux Variations Are Not Constant with Latitude for Zero Obliquity Circumbinary Planets, (3) a Circumbinary Plan
Modeling the Stellar Flux of Circumbinary Planets S. Karthik Yadavalli, Billy Quarles, Gongjie Li Center for Relativistic Astrophysics, School of Physics, Georgia Institute of Technology, Atlanta, GA 30332 Introduction: In the solar system, the Earth is said A circumbinary planet orbiting a G-M binary can to be in the habitable zone (HZ) of the Sun. It is within a undergo 40% flux variations near the critical range of distances from the Sun to be able to support stability limit (e.g., Quarles et al., 2018) of the binary. liquid water on the surface. Each star, based on its spectral properties, has a uniquely defined habitable zone (Haghighipour & Kaltenegger, 2013). Just as the Earth and the other planets in the solar system orbit the Sun, the other stars in the universe host planets of their own, known as exoplanets. Although the solar system is a single-star system, binary star systems are quite common. It is estimated that half of all star systems in the universe are binaries s. As such, nearly a dozen different binary star systems are known to host at least one exoplanet (e.g., Li et al. 2016). A planet that orbits 2 stars, called a circumbinary planet, is bound to have much more interesting weather patterns. The Earth, which only orbits one star, currently gets almost constant flux of stellar radiation in a near circular orbit. On the contrary, it is possible for a circumbinary planet in a near circular orbit to have wildly varying fluxes. If a circumbinary planet is within the habitable zone and indeed hosts life, an interesting question to ask is kind of flux variations would the life on such a planet endure? Methods: We use the Rebound library in python to run N-body simulations of circumbinary orbits. -

Uv Astronomy with Small Satellites
UV ASTRONOMY WITH SMALL SATELLITES Pol Ribes-Pleguezuelo(1), Fanny Keller(1), Matteo Taccola(1) (1) ESA-ESTEC, Keplerlaan 1, 2201AZ Noordwijk, Netherlands, [email protected], [email protected], [email protected] ABSTRACT Small satellite platforms with high performance avionics are becoming more affordable. So far, with a few exceptions, small satellites have been mainly dedicated to earth observation. However, astronomy is a fascinating field with a history of large missions and a future of promising large mission candidates. This prompts many questions; can the recent affordability of small satellites change the landscape of space astronomy? What are the potential applications and scientific topics of interest, where small satellites could be instrumental for astronomy? What are the requirements and objectives that need to be fulfilled to successfully address the astronomical investigations of interest? Which kind of instrumentation suits the small platforms and the scientific use cases best? This paper discusses possible scientific use cases that can be achievable with a relatively small telescope aperture of 36 cm, as an example. The result of this survey points to a specific niche market -astronomy observation in the UV spectral range. UV astronomy is a research field which has had valuable scientific impact. It is, however, not the focus of many current or past astronomical investigations. UV astronomy measurements cannot be made from earth, due to atmospheric absorption in this spectral range. Only a few current space missions, such as the Hubble and Gaia, cover the UV spectral range, some of them only in the near-UV (NUV). The research field is currently sparsely addressed but of scientific interest for a large community. -

Exploring Exoplanet Populations with NASA's Kepler Mission
SPECIAL FEATURE: PERSPECTIVE PERSPECTIVE SPECIAL FEATURE: Exploring exoplanet populations with NASA’s Kepler Mission Natalie M. Batalha1 National Aeronautics and Space Administration Ames Research Center, Moffett Field, 94035 CA Edited by Adam S. Burrows, Princeton University, Princeton, NJ, and accepted by the Editorial Board June 3, 2014 (received for review January 15, 2014) The Kepler Mission is exploring the diversity of planets and planetary systems. Its legacy will be a catalog of discoveries sufficient for computing planet occurrence rates as a function of size, orbital period, star type, and insolation flux.The mission has made significant progress toward achieving that goal. Over 3,500 transiting exoplanets have been identified from the analysis of the first 3 y of data, 100 planets of which are in the habitable zone. The catalog has a high reliability rate (85–90% averaged over the period/radius plane), which is improving as follow-up observations continue. Dynamical (e.g., velocimetry and transit timing) and statistical methods have confirmed and characterized hundreds of planets over a large range of sizes and compositions for both single- and multiple-star systems. Population studies suggest that planets abound in our galaxy and that small planets are particularly frequent. Here, I report on the progress Kepler has made measuring the prevalence of exoplanets orbiting within one astronomical unit of their host stars in support of the National Aeronautics and Space Admin- istration’s long-term goal of finding habitable environments beyond the solar system. planet detection | transit photometry Searching for evidence of life beyond Earth is the Sun would produce an 84-ppm signal Translating Kepler’s discovery catalog into one of the primary goals of science agencies lasting ∼13 h. -

Exoplanet Community Report
JPL Publication 09‐3 Exoplanet Community Report Edited by: P. R. Lawson, W. A. Traub and S. C. Unwin National Aeronautics and Space Administration Jet Propulsion Laboratory California Institute of Technology Pasadena, California March 2009 The work described in this publication was performed at a number of organizations, including the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (NASA). Publication was provided by the Jet Propulsion Laboratory. Compiling and publication support was provided by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not constitute or imply its endorsement by the United States Government, or the Jet Propulsion Laboratory, California Institute of Technology. © 2009. All rights reserved. The exoplanet community’s top priority is that a line of probeclass missions for exoplanets be established, leading to a flagship mission at the earliest opportunity. iii Contents 1 EXECUTIVE SUMMARY.................................................................................................................. 1 1.1 INTRODUCTION...............................................................................................................................................1 1.2 EXOPLANET FORUM 2008: THE PROCESS OF CONSENSUS BEGINS.....................................................2 -

What Is CHEOPS?
Swiss and ESA satellite CHEOPS launching soon! CHEOPS will be launching into space on the 17th of December! You may be wondering: what is CHEOPS? CHEOPS stands for CHaracterising ExOPlanet Satellite. Its goal is to study transits of already-known exoplanets to gain more knowledge about them. What type of information are we looking for? Scientists want to know detailed information about planets outside our Solar System, such as the mass, planet size, and density, which will in turn help to figure out the composition of these exoplanets. Studying exoplanet composition and their atmospheres is important especially for astrobiology. A planet’s chemical composition can affect its habitability for life as we know it. Scientists usually look for biosignatures such as the presence of methane or oxygen in the planet’s atmosphere, which could indicate presence of past or present life. Artist’s impression of CHEOPS. Credits: ESA / ATG medialab. The major contributors CHEOPS is a collaboration between ESA and the Swiss Space Office. The mission was proposed and is now headed by Prof. Willy Benz, from the University of Bern, which houses the mission’s consortium. The science operations consortium is at the University of Geneva, where they have many collaborators, such as the Swiss Space Center at EPFL. As it is an ESA endeavour, many other European institutions are also contributing to the mission. For example, the mission operations consortium is located in Torrejón de Ardoz, Spain. The launch The satellite has already been shipped to Kourou, French Guiana, where it will be launched by the ESA spaceport. -

Recipe for a Habitable Planet
Recipe for a Habitable Planet Aomawa Shields Clare Boothe Luce Associate Professor Shields Center for Exoplanet Climate and Interdisciplinary Education (SCECIE) University of California, Irvine ASU School of Earth and Space Exploration (SESE) December 2, 2020 A moment to pause… Leading effectively during COVID-19 • Employees Need Trust and Compassion: Be Present, Even When You're Distant • Employees Need Stability: Prioritize Wellbeing Amid Disruption • Employees Need Hope: Anchor to Your "True North" From “3 strategies for leading effectively during COVID-19” (https://www.gallup.com/workplace/306503/strategies-leading-effectively-amid-covid.aspx) Hobbies: reading movies, shows knitting mixed media/collage violin tea yoga good restaurants spa days the beach hiking smelling flowers hanging with family BINGO Ill. Niklas Elmehed. Ill. Niklas Elmehed. © Nobel Media. © Nobel Media. RadialVelocity (m/s) Nobel Prize in Physics 2019 Mayor & Queloz 1995 https://exoplanets.nasa.gov/ As of December 2, 2020 Aomawa Shields Recipe for a Habitable World Credit: NASA NNASA’sASA’s KKeplerepler MMissionission TESS Transiting Exoplanet Survey Satellite Credit: NASA-JPL/Caltech Proxima Centauri b Credit: ESO/M. Kornmesser LHS 1140b Credit: ESO TOI 700d Credit: NASA TESS planets in the Earth-sized regime Credit: NASA’s Goddard Space Flight Center Which ones do we follow up on? 20 The Habitable Zone (Kasting et al. 1993, Kopparapu et al. 2013) ) Runaway greenhouse Maximum CO2 greenhouse Stellar Mass (M Mass Stellar Distance from Star (AU) Snowball Earth Many factors can affect planetary habitability Aomawa Shields Recipe for a Habitable World Liquid water Aomawa Shields Recipe for a Habitable World Isotopic Birth Tides Orbit Abundance Environ. -

Satellite Splat II: an Inelastic Collision with a Surface-Launched Projectile and the Maximum Orbital Radius for Planetary Impact
European Journal of Physics Eur. J. Phys. 37 (2016) 045004 (10pp) doi:10.1088/0143-0807/37/4/045004 Satellite splat II: an inelastic collision with a surface-launched projectile and the maximum orbital radius for planetary impact Philip R Blanco1,2,4 and Carl E Mungan3 1 Department of Physics and Astronomy, Grossmont College, El Cajon, CA 92020- 1765, USA 2 Department of Astronomy, San Diego State University, San Diego, CA 92182- 1221, USA 3 Physics Department, US Naval Academy, Annapolis, MD 21402-1363, USA E-mail: [email protected] Received 26 January 2016, revised 3 April 2016 Accepted for publication 14 April 2016 Published 16 May 2016 Abstract Starting with conservation of energy and angular momentum, we derive a convenient method for determining the periapsis distance of an orbiting object, by expressing its velocity components in terms of the local circular speed. This relation is used to extend the results of our previous paper, examining the effects of an adhesive inelastic collision between a projectile launched from the surface of a planet (of radius R) and an equal-mass satellite in a circular orbit of radius rs. We show that there is a maximum orbital radius rs ≈ 18.9R beyond which such a collision cannot cause the satellite to impact the planet. The difficulty of bringing down a satellite in a high orbit with a surface- launched projectile provides a useful topic for a discussion of orbital angular momentum and energy. The material is suitable for an undergraduate inter- mediate mechanics course. Keywords: orbital motion, momentum conservation, energy conservation, angular momentum, ballistics (Some figures may appear in colour only in the online journal) 4 Author to whom any correspondence should be addressed.