Replication of Coulomb's Torsion Balance Experiment
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Alexander Graham Bell 1847-1922
NATIONAL ACADEMY OF SCIENCES OF THE UNITED STATES OF AMERICA BIOGRAPHICAL MEMOIRS VOLUME XXIII FIRST MEMOIR BIOGRAPHICAL MEMOIR OF ALEXANDER GRAHAM BELL 1847-1922 BY HAROLD S. OSBORNE PRESENTED TO THE ACADEMY AT THE ANNUAL MEETING, 1943 It was the intention that this Biographical Memoir would be written jointly by the present author and the late Dr. Bancroft Gherardi. The scope of the memoir and plan of work were laid out in cooperation with him, but Dr. Gherardi's untimely death prevented the proposed collaboration in writing the text. The author expresses his appreciation also of the help of members of the Bell family, particularly Dr. Gilbert Grosvenor, and of Mr. R. T. Barrett and Mr. A. M. Dowling of the American Telephone & Telegraph Company staff. The courtesy of these gentlemen has included, in addition to other help, making available to the author historic documents relating to the life of Alexander Graham Bell in the files of the National Geographic Society and in the Historical Museum of the American Telephone and Telegraph Company. ALEXANDER GRAHAM BELL 1847-1922 BY HAROLD S. OSBORNE Alexander Graham Bell—teacher, scientist, inventor, gentle- man—was one whose life was devoted to the benefit of mankind with unusual success. Known throughout the world as the inventor of the telephone, he made also other inventions and scientific discoveries of first importance, greatly advanced the methods and practices for teaching the deaf and came to be admired and loved throughout the world for his accuracy of thought and expression, his rigid code of honor, punctilious courtesy, and unfailing generosity in helping others. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -
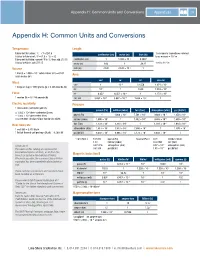
Appendix H: Common Units and Conversions Appendices 215
Appendix H: Common Units and Conversions Appendices 215 Appendix H: Common Units and Conversions Temperature Length Fahrenheit to Celsius: °C = (°F-32)/1.8 1 micrometer (sometimes referred centimeter (cm) meter (m) inch (in) Celsius to Fahrenheit: °F = (1.8 × °C) + 32 to as micron) = 10-6 m Fahrenheit to Kelvin: convert °F to °C, then add 273.15 centimeter (cm) 1 1.000 × 10–2 0.3937 -3 Celsius to Kelvin: add 273.15 meter (m) 100 1 39.37 1 mil = 10 in Volume inch (in) 2.540 2.540 × 10–2 1 –3 3 1 liter (l) = 1.000 × 10 cubic meters (m ) = 61.02 Area cubic inches (in3) cm2 m2 in2 circ mil Mass cm2 1 10–4 0.1550 1.974 × 105 1 kilogram (kg) = 1000 grams (g) = 2.205 pounds (lb) m2 104 1 1550 1.974 × 109 Force in2 6.452 6.452 × 10–4 1 1.273 × 106 1 newton (N) = 0.2248 pounds (lb) circ mil 5.067 × 10–6 5.067 × 10–10 7.854 × 10–7 1 Electric resistivity Pressure 1 micro-ohm-centimeter (µΩ·cm) pascal (Pa) millibar (mbar) torr (Torr) atmosphere (atm) psi (lbf/in2) = 1.000 × 10–6 ohm-centimeter (Ω·cm) –2 –3 –6 –4 = 1.000 × 10–8 ohm-meter (Ω·m) pascal (Pa) 1 1.000 × 10 7.501 × 10 9.868 × 10 1.450 × 10 = 6.015 ohm-circular mil per foot (Ω·circ mil/ft) millibar (mbar) 1.000 × 102 1 7.502 × 10–1 9.868 × 10–4 1.450 × 10–2 2 0 –3 –2 Heat flow rate torr (Torr) 1.333 × 10 1.333 × 10 1 1.316 × 10 1.934 × 10 5 3 2 1 1 watt (W) = 3.413 Btu/h atmosphere (atm) 1.013 × 10 1.013 × 10 7.600 × 10 1 1.470 × 10 1 British thermal unit per hour (Btu/h) = 0.2930 W psi (lbf/in2) 6.897 × 103 6.895 × 101 5.172 × 101 6.850 × 10–2 1 1 torr (Torr) = 133.332 pascal (Pa) 1 pascal (Pa) = 0.01 millibar (mbar) 1.33 millibar (mbar) 0.007501 torr (Torr) –6 A Note on SI 0.001316 atmosphere (atm) 9.87 × 10 atmosphere (atm) 2 –4 2 The values in this catalog are expressed in 0.01934 psi (lbf/in ) 1.45 × 10 psi (lbf/in ) International System of Units, or SI (from the Magnetic induction B French Le Système International d’Unités). -

Electricity and Magnetism
Lecture 10 Fundamentals of Physics Phys 120, Fall 2015 Electricity and Magnetism A. J. Wagner North Dakota State University, Fargo, ND 58102 Fargo, September 24, 2015 Overview • Unexplained phenomena • Charges and electric forces revealed • Currents and circuits • Electricity and Magnetism are related! 1 Newton’s dream I wish we could derive the rest of the phenomena of Nature by the same kind of reasoning from mechanical principles, for I am induced by many reasons to suspect that they may all depend upon certain forces by which the particles of bodies, by some cause hitherto unknown, are either mutually impelled towards one another, and cohere in regular figures, or are repelled and recede from one another. from the preface of Newton’s Principia 2 What were those mysterious phenomena? 900 BC: Magnus, a Greek shepherd, walks across a field of black stones which pull the iron nails out of his sandals and the iron tip from his shepherd’s staff (authenticity not guaranteed). This region becomes known as Magnesia. 600 BC: Thales of Miletos(Greece) discovered that by rubbing an ’elektron’ (a hard, fossilized resin that today is known as amber) against a fur cloth, it would attract particles of straw and feathers. This strange effect remained a mystery for over 2000 years. 1269 AD: Petrus Peregrinus of Picardy, Italy, discovers that natural spherical magnets (lodestones) align needles with lines of longitude pointing between two pole positions on the stone. 3 ca. 1600: Dr.William Gilbert (court physician to Queen Elizabeth) discovers that the earth is a giant magnet just like one of the stones of Peregrinus, explaining how compasses work. -

Historical Perspective of Electricity
B - Circuit Lab rev.1.04 - December 19 SO Practice - 12-19-2020 Just remember, this test is supposed to be hard because everyone taking this test is really smart. Historical Perspective of Electricity 1. (1.00 pts) The first evidence of electricity in recorded human history was… A) in 1752 when Ben Franklin flew his kite in a lightning storm. B) in 1600 when William Gilbert published his book on magnetism. C) in 1708 when Charles-Augustin de Coulomb held a lecture stating that two bodies electrified of the same kind of Electricity exert force on each other. D) in 1799 when Alessandro Volta invented the voltaic pile which proved that electricity could be generated chemically. E) in 1776 when André-Marie Ampère invented the electric telegraph. F) about 2500 years ago when Thales of Miletus noticed that a piece of amber attracted straw or feathers when he rubbed it with cloth. 2. (3.00 pts) The word electric… (Mark ALL correct answers) A) was first used in printed text when it was published in William Gilber’s book on magnetism. B) comes from the Greek word ήλεκτρο (aka “electron”) meaning amber. C) adapted the meaning “charged with electricity” in the 1670s. D) was first used by Nicholas Callen in 1799 to describe mail transmitted over telegraph wires, “electric-mail” or “email”. E) was cast in stone by Greek emperor Julius Caesar when he knighted Archimedes for inventing the electric turning lathe. F) was first used by Michael Faraday when he described electromagnetic induction in 1791. 3. (5.00 pts) Which five people, who made scientific discoveries related to electricity, were alive at the same time? (Mark ALL correct answers) A) Charles-Augustin de Coulomb B) Alessandro Volta C) André-Marie Ampère D) Georg Simon Ohm E) Michael Faraday F) Gustav Robert Kirchhoff 4. -

CAR-ANS PART 05 Issue No. 2 Units of Measurement to Be Used In
CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES Part 5 Governing UNITS OF MEASUREMENT TO BE USED IN AIR AND GROUND OPERATIONS CIVIL AVIATION AUTHORITY OF THE PHILIPPINES Old MIA Road, Pasay City1301 Metro Manila INTENTIONALLY LEFT BLANK CAR-ANS PART 5 Republic of the Philippines CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES (CAR-ANS) Part 5 UNITS OF MEASUREMENTS TO BE USED IN AIR AND GROUND OPERATIONS 22 APRIL 2016 EFFECTIVITY Part 5 of the Civil Aviation Regulations-Air Navigation Services are issued under the authority of Republic Act 9497 and shall take effect upon approval of the Board of Directors of the CAAP. APPROVED BY: LT GEN WILLIAM K HOTCHKISS III AFP (RET) DATE Director General Civil Aviation Authority of the Philippines Issue 2 15-i 16 May 2016 CAR-ANS PART 5 FOREWORD This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was formulated and issued by the Civil Aviation Authority of the Philippines (CAAP), prescribing the standards and recommended practices for units of measurements to be used in air and ground operations within the territory of the Republic of the Philippines. This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was developed based on the Standards and Recommended Practices prescribed by the International Civil Aviation Organization (ICAO) as contained in Annex 5 which was first adopted by the council on 16 April 1948 pursuant to the provisions of Article 37 of the Convention of International Civil Aviation (Chicago 1944), and consequently became applicable on 1 January 1949. The provisions contained herein are issued by authority of the Director General of the Civil Aviation Authority of the Philippines and will be complied with by all concerned. -

The International System of Units (SI) - Conversion Factors For
NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v -

JJ Thomson Discovered the Electron in Experiments Looking At
1897 – JJ Thomson discovered the electron in experiments looking at electric discharge in a high-vacuum cathode-ray tube. He interpreted the deflection of the rays by electrically charged plates and magnets as evidence of "particles much smaller than atoms" 1896 – Henri Becquerel – Though fascinated by materials that exhibited phosphorescence, it was through experiments involving non-phosphorescent uranium salts that he gained his real notoriety. While experimenting with these materials, he discovered natural radioactivity. Through his experiment, he determined that the penetrating radiation came from the uranium itself, without any need of excitation by an external energy source. 1895 – Wilhelm Röentgen – During an experiment, he noticed photographic plates near his equipment glowing. He discovered the glowing was caused by rays emitted by the glass tube used in his investigation. This tube contained a pair of electrodes. As electricity passed between the electrodes, X‑rays were emitted and appeared on the photographic plates. 1887 – Svante Arrhenius ACID = neutral compound that ionizes when dissolved in water and produces the H+ ion and corresponding negative ion. BASE = neutral compound that either dissociates or ionizes in water to give OH- ions and a corresponding positive ion. 1806 - Gay-Lussac - Gay-Lussac's Law states that at constant volume, the pressure of a sample of gas is directly proportional to its temperature in Kelvin. He also provided us with the law of combining volumes - when gases react, the volumes consumed and produced, measured at the same temperature and pressure, are in ratios of small whole numbers. 1804 – John Dalton Once again contributed to the chemical world and gave us the Law of Multiple Proportions – If the same two elements form more than one compound between them, then the combining mass ratios of the two compounds will NOT be the same. -

Physics 2. Class #1. Welcome to Electricity and Magnetism September 17, 2017
Physics 2. Class #1. Welcome to Electricity and Magnetism September 17, 2017 Remembering last year. In our experiments with colliding carts we noticed that if you add up the change of velocity of one cart times some number m (which is specific for that cart 1) and the change of velocity of the second one times another number m’ (which is specific for that cart 2) then the sum is zero: 푚∆푣 + 푚∆푣 =0 We named these m’s “masses”... So there was a property of that system which was not changing ∆(푚푣 + 푚푣) =0 We called that quantity “momentum”, the general definition for the system made of 푛 constituents is: 푝 = 푚푣 Where the index 푖 runs over all the pieces which are included in the system. If nothing acts on the system from outside, this 푝 does not change over time : ∆푝 =0 . But if there is something that influences this system from outside, then the longer it acts, the larger is the disturbance. We named this reason for changing of the momentum “the force” and, to reflect that the longer it acts, the bigger is the change, we wrote the definition of the force as ∆푝⃗ = 퐹⃗ ∆푡 Forces in Nature Interaction Relative strength Radius of action, cm Observed in Gravitational 10 ∞ Cosmos Strong 100 10 Nuclei, Elementary particles Weak 10 10 Elementary particles transformations Electromagnetic 1 ∞ From Nucleus to Cosmos Page 1 Physics 2. Class #1. Welcome to Electricity and Magnetism September 17, 2017 A brief story of modern electromagnetic theory. Year 1600 William Gilbert (England) «De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure» (On the Magnet and Magnetic Bodies, and on That Great Magnet the Earth) ήλεκτρον is (old) Greek for “amber” Page 2 Physics 2. -

International System of Electric and Magnetic Units
.. INTERNATIONAL SYSTEM OF ELECTRIC AND MAGNETIC UNITS By J. H. Dellinger CONTENTS Page I. Introduction 599 II. The international system 600 1 Simplicity of this system 604 2 Subordination of the magnetic pole. 605 3 Limitation to electromagnetism 605 III. The magnetic quantities 606 1 The magnetic circuit 607 2 Induction and magnetizing force 608 IV. Rationalization of the units 613 1. The Heaviside system 613 2 Other attempts to eliminate 47r 616 3. The two sets of magnetic units 621 4. The ampere-turn units 623 V. Summary 628 Appendix.—Symbols used 631 I. INTRODUCTION Electric units and standards are now very nearly uniform in all parts of the world. As a result of the decisions of international congresses and the cooperation of the national standardizing laboratories, the international ohm and ampere are accepted every- where as the basis of electrical measurements. A complete system of electric and magnetic imits is in general use, built upon these fundamental units. There have been proposals to change the units from time to time, and as a result there is some diversity of usage in respect to units in current electric and magnetic literature. For instance, Heaviside iinits are used in certain recent books on theoretical electricity ; a slight change of electric units is advocated by M. Abraham; and quite a number of different magnetic units are used in presenting the results of magnetic experiments. It appears worth while to examine critically the system of imits which is generally used, to study the reasons which are advanced 599 6oo Bulletin of the Bureau of Standards [Voi. -

I. Electric Charge I
2 I. Electric Charge I. Electric Charge A. History of Electricity Dr. Bill Pezzaglia B. Coulomb’s Law C. Electrodynamics Updated 2014Feb03 3 1a. Thales of Miletos (624-454 BC) 4 A. History of Electricity • Famous theorems of similar triangles 1) The Electric Effect • Amber rubbed with fur attracts straw 2) Charging Methods • “Amber” in greek: “elektron” 3) Measuring Charge Here is a narrow tomb Great Thales lies; yet his renown for wisdom reached the skies 5 6 1.b. William Gilbert (1544-1603) 1.c. Stephen Gray (1696-1736) [student of Newton!] •“Father of Science” (i.e. use experiments instead of citing ancient authority) • 1729 does experiment showing electric effects can •1600 Book “De Magnete” travel over great distance – Originates term “electricity” through a thread or wire. – Distinguishes between electric and magnetic force – Influences Kepler & Galileo • Classifies Materials as: – Glass rubbed with Silk attracts – Conductors: which can objects remove charge from a body – Insulators: that do not. •Invented “Versorium” (needle) used to measure electric force 1 7 8 1.d. Charles Dufay (1689-1739) 1.e. Benjamin Franklin (1706-1790) •1733 Proposes “two fluid” theory of electricity •1752 Kite Experiment proves lightening is electric – Vitreous (glass, fur) (+) – Resinous (amber, silk) (-) •Proposes single fluid but two state model of charge •Summarizes Electric Laws + + – Like fluids repel + is an excess of charge – opposite attract + - - is deficit in charge – All bodies except metals can be charged by friction – All bodies can be charged by “influence” (induction) •Charge is conserved (objects are naturally neutral) 9 Dry human skin 10 + Asbestos 2.a.1 Triboelectrification chart Leather 2. -

Units of Measure
Units of Measure Units marked with asterisks are base, derived, or supplementary units of the Systeme International. Unit Abbreviation abampere - spell out abohm - spell out abvolt - spell out amagat - spell out *ampere - A ampere hour - A h ampere turns per meter - At/m angstrom - Å arc minute - arc min astronomical unit - AU atmosphere - atm atmosphere, standard - As atomic mass unit - u atomic parts per million - at. ppm atomic percent - at. % atomic time unit - atu atomic unit- a.u. attofarad - aF bar - spell out bark - spell out barn - b barye - spell out biot - Bi bit or bits - spell out blobs per hundred microns - blobs/(100 um) bohr - spell out British thermal unit - Btu bytes - spell out calorie - cal *candela - cd candelas per square meter - cd/m2 candlepower - cp centimeter - cm centipoise - cP *coulomb - C counts per minute - counts/min, cpm counts per second - counts/s cubic centimeter - cm3, (cc not rec.) curie - Ci cycle - spell out, c cycles per second - cps, c/s day d, - or spell out debye - D decibel - dB, dBm degree - [ring], deg degrees - Baumé [ring]B degrees - Celsius (centigrade) [ring]C degrees - Fahrenheit [ring]F degrees - Kelvin K disintegrations per minute - dis/min disintegrations per minute per microgram - dis/min ug disintegrations per second - dis/s dyne - dyn electromagnetic unit - emu electron barn - eb electrons per atom - e/at. electrons per cubic centimeter - e/cm3, e/cc, e cm-3 electron unit - e.u. electron volt - eV electrostatic unit - esu entropy unit - eu erg - spell out *farad - F femtofarad - fF femtometer - fm fermi - F fissions per minute - fpm foot - ft foot-candle - fc foot-lambert - fL foot-pound - ft lb formula units - f.u.