Comparisons of Computational Tools for the Muon Anomalous Magnetic Moment Within the Pmssm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Pev-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability
The PeV-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability Waqas Ahmed ? 1, Adeel Mansha ? 2, Tianjun Li ? ~ 3, Shabbar Raza ∗ 4, Joydeep Roy ? 5, Fang-Zhou Xu ? 6, ? CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, P. R. China ~School of Physical Sciences, University of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing 100049, P. R. China ∗ Department of Physics, Federal Urdu University of Arts, Science and Technology, Karachi 75300, Pakistan Institute of Modern Physics, Tsinghua University, Beijing 100084, China Abstract The null results of the LHC searches have put strong bounds on new physics scenario such as supersymmetry (SUSY). With the latest values of top quark mass and strong coupling, we study the upper bounds on the sfermion masses in Split-SUSY from the observed Higgs boson mass and electroweak (EW) vacuum stability. To be consistent with the observed Higgs mass, we find that the largest value of supersymmetry breaking 3 1:5 scales MS for tan β = 2 and tan β = 4 are O(10 TeV) and O(10 TeV) respectively, thus putting an upper bound on the sfermion masses around 103 TeV. In addition, the Higgs quartic coupling becomes negative at much lower scale than the Standard Model (SM), and we extract the upper bound of O(104 TeV) on the sfermion masses from EW vacuum stability. Therefore, we obtain the PeV-Scale Split-SUSY. The key point is the extra contributions to the Renormalization Group Equation (RGE) running from arXiv:1901.05278v1 [hep-ph] 16 Jan 2019 the couplings among Higgs boson, Higgsinos, and gauginos. -
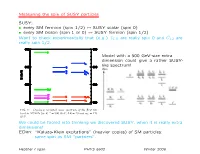
Measuring the Spin of SUSY Particles SUSY: • Every SM Fermion (Spin 1/2
Measuring the spin of SUSY particles SUSY: • every SM fermion (spin 1/2) ↔ SUSY scalar (spin 0) • every SM boson (spin 1 or 0) ↔ SUSY fermion (spin 1/2) Want to check experimentally that (e.g.) eL,R are really spin 0 and Ce1,2 are really spin 1/2. 2 preserve the 5th dimensional momentum (KK number). The corresponding coupling constants among KK modes Model with a 500 GeV-size extra are simply equal to the SM couplings (up to normaliza- tion factors such as √2). The Feynman rules for the KK dimension could give a rather SUSY- modes can easily be derived (e.g., see Ref. [8, 9]). like spectrum! In contrast, the coefficients of the boundary terms are not fixed by Standard Model couplings and correspond to new free parameters. In fact, they are renormalized by the bulk interactions and hence are scale dependent [10, 11]. One might worry that this implies that all pre- dictive power is lost. However, since the wave functions of Standard Model fields and KK modes are spread out over the extra dimension and the new couplings only exist on the boundaries, their effects are volume sup- pressed. We can get an estimate for the size of these volume suppressed corrections with naive dimensional analysis by assuming strong coupling at the cut-off. The FIG. 1: One-loop corrected mass spectrum of the first KK −1 result is that the mass shifts to KK modes from bound- level in MUEDs for R = 500 GeV, ΛR = 20 and mh = 120 ary terms are numerically equal to corrections from loops GeV. -

Electroweak Radiative B-Decays As a Test of the Standard Model and Beyond Andrey Tayduganov
Electroweak radiative B-decays as a test of the Standard Model and beyond Andrey Tayduganov To cite this version: Andrey Tayduganov. Electroweak radiative B-decays as a test of the Standard Model and beyond. Other [cond-mat.other]. Université Paris Sud - Paris XI, 2011. English. NNT : 2011PA112195. tel-00648217 HAL Id: tel-00648217 https://tel.archives-ouvertes.fr/tel-00648217 Submitted on 5 Dec 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. LAL 11-181 LPT 11-69 THESE` DE DOCTORAT Pr´esent´eepour obtenir le grade de Docteur `esSciences de l’Universit´eParis-Sud 11 Sp´ecialit´e:PHYSIQUE THEORIQUE´ par Andrey Tayduganov D´esint´egrationsradiatives faibles de m´esons B comme un test du Mod`eleStandard et au-del`a Electroweak radiative B-decays as a test of the Standard Model and beyond Soutenue le 5 octobre 2011 devant le jury compos´ede: Dr. J. Charles Examinateur Prof. A. Deandrea Rapporteur Prof. U. Ellwanger Pr´esident du jury Prof. S. Fajfer Examinateur Prof. T. Gershon Rapporteur Dr. E. Kou Directeur de th`ese Dr. A. Le Yaouanc Directeur de th`ese Dr. -

The Minimal Supersymmetric Standard Model: Group Summary Report
PM/98–45 December 1998 The Minimal Supersymmetric Standard Model: Group Summary Report Conveners: A. Djouadi1, S. Rosier-Lees2 Working Group: M. Bezouh1, M.-A. Bizouard3,C.Boehm1, F. Borzumati1;4,C.Briot2, J. Carr5,M.B.Causse6, F. Charles7,X.Chereau2,P.Colas8, L. Duflot3, A. Dupperin9, A. Ealet5, H. El-Mamouni9, N. Ghodbane9, F. Gieres9, B. Gonzalez-Pineiro10, S. Gourmelen9, G. Grenier9, Ph. Gris8, J.-F. Grivaz3,C.Hebrard6,B.Ille9, J.-L. Kneur1, N. Kostantinidis5, J. Layssac1,P.Lebrun9,R.Ledu11, M.-C. Lemaire8, Ch. LeMouel1, L. Lugnier9 Y. Mambrini1, J.P. Martin9,G.Montarou6,G.Moultaka1, S. Muanza9,E.Nuss1, E. Perez8,F.M.Renard1, D. Reynaud1,L.Serin3, C. Thevenet9, A. Trabelsi8,F.Zach9,and D. Zerwas3. 1 LPMT, Universit´e Montpellier II, F{34095 Montpellier Cedex 5. 2 LAPP, BP 110, F{74941 Annecy le Vieux Cedex. 3 LAL, Universit´e de Paris{Sud, Bat{200, F{91405 Orsay Cedex 4 CERN, Theory Division, CH{1211, Geneva, Switzerland. 5 CPPM, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. 6 LPC Clermont, Universit´e Blaise Pascal, F{63177 Aubiere Cedex. 7 GRPHE, Universit´e de Haute Alsace, Mulhouse 8 SPP, CEA{Saclay, F{91191 Cedex 9 IPNL, Universit´e Claude Bernard de Lyon, F{69622 Villeurbanne Cedex. 10 LPNHE, Universit´es Paris VI et VII, Paris Cedex. 11 CPT, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. Report of the MSSM working group for the Workshop \GDR{Supersym´etrie". 1 CONTENTS 1. Synopsis 4 2. The MSSM Spectrum 9 2.1 The MSSM: Definitions and Properties 2.1.1 The uMSSM: unconstrained MSSM 2.1.2 The pMSSM: “phenomenological” MSSM 2.1.3 mSUGRA: the constrained MSSM 2.1.4 The MSSMi: the intermediate MSSMs 2.2 Electroweak Symmetry Breaking 2.2.1 General features 2.2.2 EWSB and model–independent tanβ bounds 2.3 Renormalization Group Evolution 2.3.1 The one–loop RGEs 2.3.2 Exact solutions for the Yukawa coupling RGEs 3. -

The Magnetic Dipole Moment of the Muon in Different SUSY Models
The magnetic dipole moment of the muon in different SUSY models Bachelor-Arbeit zur Erlangung des Hochschulgrades Bachelor of Science im Bachelor-Studiengang Physik vorgelegt von Jobst Ziebell geboren am 05.11.1992 in Herrljunga Institut für Kern- und Teilchenphysik Fachrichtung Physik Fakultät Mathematik und Naturwissenschaften Technische Universität Dresden 2015 Eingereicht am 1. Juli 2015 1. Gutachter: Prof. Dr. Dominik Stöckinger 2. Gutachter: Prof. Dr. Kai Zuber Abstract The magnetic dipole moment of the muon is one of the most precisely measured quantities in modern physics. Theory however predicts values that disagree with measurement by several standard deviations [1, Abstract]. Because this may hint at physics beyond the standard model, it is a great opportunity to ex- amine the magnetic dipole moment in different supersymmetric models. It is then possible to calculate dependences of the dipole moment on various model parameters as well as to find constraints for their particular values. The purpose of this paper is to describe how the magnetic dipole moment is obtained in su- persymmetric extensions of the standard model and to document the implementation of its calculation in FlexibleSUSY, a spectrum generator for supersymmetric models [2, Abstract]. Contents 1 Introduction 1 2 The gyromagnetic ratio 2 2.1 In classical mechanics . .2 2.2 In quantum mechanics . .3 2.3 In quantum field theory . .4 3 The implementation in FlexibleSUSY 7 3.1 The C++ part . .7 3.2 The Mathematica part . 11 3.3 The FlexibleSUSY part . 12 4 Results 13 Appendices 17 A The Loop functions . 17 B The VertexFunction template . 17 C The DiagramEvaluator<...>::value() functions . -

Arxiv:Astro-Ph/0010112 V2 10 Apr 2001
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CERN Document Server NYU-TH-00/09/05 Preprint typeset using LATEX style emulateapj v. 14/09/00 NEUTRON STARS WITH A STABLE, LIGHT SUPERSYMMETRIC BARYON SHMUEL BALBERG1,GLENNYS R. FARRAR2 AND TSVI PIRAN3 NYU-TH-00/09/05 ABSTRACT ¼ If a light gluino exists, the lightest gluino-containing baryon, the Ë , is a possible candidate for self-interacting ¼ ª =ª 6 ½¼ Ñ dÑ b dark matter. In this scenario, the simplest explanation for the observed ratio is that Ë ¼ ¾ Ë 9¼¼ MeVc ; this is not at present excluded by particle physics. Such an could be present in neutron stars, with hyperon formation serving as an intermediate stage. We calculate equilibrium compositions and equation of ¼ state for high density matter with the Ë , and find that for a wide range of parameters the properties of neutron ¼ stars with the Ë are consistent with observations. In particular, the maximum mass of a nonrotating star is ¼ ½:7 ½:8 Å Ë ¬ , and the presence of the is helpful in reconciling observed cooling rates with hyperon formation. Subject headings: dark matter–dense matter–elementary particles–equation of state–stars: neutron 1. INTRODUCTION also Farrar & Gabadadze (2000) and references therein. The lightest supersymmetric “Ê-hadrons” are the spin-1/2 The interiors of neutron stars offer a unique meeting point ¼ gg Ê ~ bound state ( or glueballino) and the spin-0 baryon between astrophysics on one hand and nuclear and particle ¼ ¼ g~ Ë Ë Ùd× bound state, the .The is thus a boson with baryon physics on the other. -

Supersymmetric Particle Searches
Citation: K.A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014) (URL: http://pdg.lbl.gov) Supersymmetric Particle Searches A REVIEW GOES HERE – Check our WWW List of Reviews A REVIEW GOES HERE – Check our WWW List of Reviews SUPERSYMMETRIC MODEL ASSUMPTIONS The exclusion of particle masses within a mass range (m1, m2) will be denoted with the notation “none m m ” in the VALUE column of the 1− 2 following Listings. The latest unpublished results are described in the “Supersymmetry: Experiment” review. A REVIEW GOES HERE – Check our WWW List of Reviews CONTENTS: χ0 (Lightest Neutralino) Mass Limit 1 e Accelerator limits for stable χ0 − 1 Bounds on χ0 from dark mattere searches − 1 χ0-p elastice cross section − 1 eSpin-dependent interactions Spin-independent interactions Other bounds on χ0 from astrophysics and cosmology − 1 Unstable χ0 (Lighteste Neutralino) Mass Limit − 1 χ0, χ0, χ0 (Neutralinos)e Mass Limits 2 3 4 χe ,eχ e(Charginos) Mass Limits 1± 2± Long-livede e χ± (Chargino) Mass Limits ν (Sneutrino)e Mass Limit Chargede Sleptons e (Selectron) Mass Limit − µ (Smuon) Mass Limit − e τ (Stau) Mass Limit − e Degenerate Charged Sleptons − e ℓ (Slepton) Mass Limit − q (Squark)e Mass Limit Long-livede q (Squark) Mass Limit b (Sbottom)e Mass Limit te (Stop) Mass Limit eHeavy g (Gluino) Mass Limit Long-lived/lighte g (Gluino) Mass Limit Light G (Gravitino)e Mass Limits from Collider Experiments Supersymmetrye Miscellaneous Results HTTP://PDG.LBL.GOV Page1 Created: 8/21/2014 12:57 Citation: K.A. Olive et al. -

R-Parity Violation and Light Neutralinos at Ship and the LHC
BONN-TH-2015-12 R-Parity Violation and Light Neutralinos at SHiP and the LHC Jordy de Vries,1, ∗ Herbi K. Dreiner,2, y and Daniel Schmeier2, z 1Institute for Advanced Simulation, Institut f¨urKernphysik, J¨ulichCenter for Hadron Physics, Forschungszentrum J¨ulich, D-52425 J¨ulich, Germany 2Physikalisches Institut der Universit¨atBonn, Bethe Center for Theoretical Physics, Nußallee 12, 53115 Bonn, Germany We study the sensitivity of the proposed SHiP experiment to the LQD operator in R-Parity vi- olating supersymmetric theories. We focus on single neutralino production via rare meson decays and the observation of downstream neutralino decays into charged mesons inside the SHiP decay chamber. We provide a generic list of effective operators and decay width formulae for any λ0 cou- pling and show the resulting expected SHiP sensitivity for a widespread list of benchmark scenarios via numerical simulations. We compare this sensitivity to expected limits from testing the same decay topology at the LHC with ATLAS. I. INTRODUCTION method to search for a light neutralino, is via the pro- duction of mesons. The rate for the latter is so high, Supersymmetry [1{3] is the unique extension of the ex- that the subsequent rare decay of the meson to the light ternal symmetries of the Standard Model of elementary neutralino via (an) R-parity violating operator(s) can be particle physics (SM) with fermionic generators [4]. Su- searched for [26{28]. This is analogous to the production persymmetry is necessarily broken, in order to comply of neutrinos via π or K-mesons. with the bounds from experimental searches. -

Introduction to Supersymmetry
Introduction to Supersymmetry Pre-SUSY Summer School Corpus Christi, Texas May 15-18, 2019 Stephen P. Martin Northern Illinois University [email protected] 1 Topics: Why: Motivation for supersymmetry (SUSY) • What: SUSY Lagrangians, SUSY breaking and the Minimal • Supersymmetric Standard Model, superpartner decays Who: Sorry, not covered. • For some more details and a slightly better attempt at proper referencing: A supersymmetry primer, hep-ph/9709356, version 7, January 2016 • TASI 2011 lectures notes: two-component fermion notation and • supersymmetry, arXiv:1205.4076. If you find corrections, please do let me know! 2 Lecture 1: Motivation and Introduction to Supersymmetry Motivation: The Hierarchy Problem • Supermultiplets • Particle content of the Minimal Supersymmetric Standard Model • (MSSM) Need for “soft” breaking of supersymmetry • The Wess-Zumino Model • 3 People have cited many reasons why extensions of the Standard Model might involve supersymmetry (SUSY). Some of them are: A possible cold dark matter particle • A light Higgs boson, M = 125 GeV • h Unification of gauge couplings • Mathematical elegance, beauty • ⋆ “What does that even mean? No such thing!” – Some modern pundits ⋆ “We beg to differ.” – Einstein, Dirac, . However, for me, the single compelling reason is: The Hierarchy Problem • 4 An analogy: Coulomb self-energy correction to the electron’s mass A point-like electron would have an infinite classical electrostatic energy. Instead, suppose the electron is a solid sphere of uniform charge density and radius R. An undergraduate problem gives: 3e2 ∆ECoulomb = 20πǫ0R 2 Interpreting this as a correction ∆me = ∆ECoulomb/c to the electron mass: 15 0.86 10− meters m = m + (1 MeV/c2) × . -

Beyond the Standard Model
Beyond the Standard Model Mihoko M. Nojiri Theory Center, IPNS, KEK, Tsukuba, Japan, and Kavli IPMU, The University of Tokyo, Kashiwa, Japan Abstract A Brief review on the physics beyond the Standard Model. 1 Quest of BSM Although the standard model of elementary particles(SM) describes the high energy phenomena very well, particle physicists have been attracted by the physics beyond the Standard Model (BSM). There are very good reasons about this; 1. The SM Higgs sector is not natural. 2. There is no dark matter candidate in the SM. 3. Origin of three gauge interactions is not understood in the SM. 4. Cosmological observations suggest an inflation period in the early universe. The non-zero baryon number of our universe is not consistent with the inflation picture unless a new interaction is introduced. The Higgs boson candidate was discovered recently. The study of the Higgs boson nature is extremely important for the BSM study. The Higgs boson is a spin 0 particle, and the structure of the radiative correction is quite different from those of fermions and gauge bosons. The correction of the Higgs boson mass is proportional to the cut-off scale, called “quadratic divergence". If the cut-off scale is high, the correction becomes unacceptably large compared with the on-shell mass of the Higgs boson. This is often called a “fine turning problem". Note that such quadratic divergence does not appear in the radiative correction to the fermion and gauge boson masses. They are protected by the chiral and gauge symmetries, respectively. The problem can be solved if there are an intermediate scale where new particles appears, and the radiative correction from the new particles compensates the SM radiative correction. -

Supersymmetry: What? Why? When?
Contemporary Physics, 2000, volume41, number6, pages359± 367 Supersymmetry:what? why? when? GORDON L. KANE This article is acolloquium-level review of the idea of supersymmetry and why so many physicists expect it to soon be amajor discovery in particle physics. Supersymmetry is the hypothesis, for which there is indirect evidence, that the underlying laws of nature are symmetric between matter particles (fermions) such as electrons and quarks, and force particles (bosons) such as photons and gluons. 1. Introduction (B) In addition, there are anumber of questions we The Standard Model of particle physics [1] is aremarkably hope will be answered: successful description of the basic constituents of matter (i) Can the forces of nature be uni® ed and (quarks and leptons), and of the interactions (weak, simpli® ed so wedo not have four indepen- electromagnetic, and strong) that lead to the structure dent ones? and complexity of our world (when combined with gravity). (ii) Why is the symmetry group of the Standard It is afull relativistic quantum ®eld theory. It is now very Model SU(3) ´SU(2) ´U(1)? well tested and established. Many experiments con® rmits (iii) Why are there three families of quarks and predictions and none disagree with them. leptons? Nevertheless, weexpect the Standard Model to be (iv) Why do the quarks and leptons have the extendedÐ not wrong, but extended, much as Maxwell’s masses they do? equation are extended to be apart of the Standard Model. (v) Can wehave aquantum theory of gravity? There are two sorts of reasons why weexpect the Standard (vi) Why is the cosmological constant much Model to be extended. -

Supersymmetry Min Raj Lamsal Department of Physics, Prithvi Narayan Campus, Pokhara Min [email protected]
Supersymmetry Min Raj Lamsal Department of Physics, Prithvi Narayan Campus, Pokhara [email protected] Abstract : This article deals with the introduction of supersymmetry as the latest and most emerging burning issue for the explanation of nature including elementary particles as well as the universe. Supersymmetry is a conjectured symmetry of space and time. It has been a very popular idea among theoretical physicists. It is nearly an article of faith among elementary-particle physicists that the four fundamental physical forces in nature ultimately derive from a single force. For years scientists have tried to construct a Grand Unified Theory showing this basic unity. Physicists have already unified the electron-magnetic and weak forces in an 'electroweak' theory, and recent work has focused on trying to include the strong force. Gravity is much harder to handle, but work continues on that, as well. In the world of everyday experience, the strengths of the forces are very different, leading physicists to conclude that their convergence could occur only at very high energies, such as those existing in the earliest moments of the universe, just after the Big Bang. Keywords: standard model, grand unified theories, theory of everything, superpartner, higgs boson, neutrino oscillation. 1. INTRODUCTION unifies the weak and electromagnetic forces. The What is the world made of? What are the most basic idea is that the mass difference between photons fundamental constituents of matter? We still do not having zero mass and the weak bosons makes the have anything that could be a final answer, but we electromagnetic and weak interactions behave quite have come a long way.