A Hermite-Gaussian Based Radial Velocity Estimation Method
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
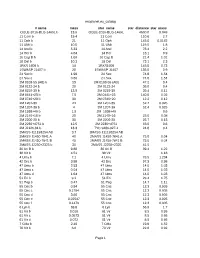
Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55 -

What Can the Dispersed Matter Planet Project Do for ARIEL?
What can the Dispersed Matter Planet Project do for ARIEL? Carole Haswell, The Open University Principal Collaborators: Dan Staab, John Barnes, Luca Fossati, MarK Jones, GuilleM Angelada-Escude, JaMes Doherty, Joe Cooper, JaMes Jenkins Outline • motivation: WASP-12: stellar activity masked by planetary mass loss new way to select host stars of ablating planets • Dispersed Matter Planet Project (DMPP) Search for Them among BRIGHT NEARBY STARS! Very efficient RV planet search 39 initial targets, good success rate • First discoveries DMPP-1, DMPP-2, DMPP-3 … • Characterisation of DMPP planets mass-radius-composition relationships, exogeology • DMPP systems good for characterisation even if not transiting… Activity: characterised by RHK Line core Emission strength Fossati, Ayres, Haswell, Bohlender, Kochukhov & Floer 2013, ApJLett Ca II H& K line cores Activity: characterised by RHK Line core emission quenched by diffuse gas Dan Staab PhD work Haswell, Staab, Barnes, Anglada-Escude, Fossati, Jenkins, Norton, Doherty, Cooper 2019, Nature Astronomy arXiv:1912.10874 Activity: characterised by RHK > 40% of close-in planet hosts: depressed CaII H&K OU-SALT survey Doherty, Haswell, Barnes, Staab, Fossati 2018, Poster Cool Stars 20; 2019 in prep Staab, Haswell, Smith, Fossati, Barnes, Busuttil, Jenkins, MNRAS, 2017, 466, 738 Absorbing gas constrained to orbital plane? Haswell, Fossati, Ayres, France, Froning et al 2012, ApJ, 760, 79 Mass-losing Close-in planets e.g. Kepler 1520b have HUGE sCale-heights KIC 1255b aka Kepler 1520b: • DeteCted by transiting -

Institute of Astrophysics and Space Sciences 2018 Activity Report
Institute of Astrophysics and Space Sciences 2018 Activity Report Institute of Astrophysics and Space Sciences 2018 Activity Report COFINANCIAMENTO 2018 IA ACTIVITY REPORT | 3 Index Unit Overview 5 IA Management 6 Visitor Program at the Institute for Astrophysics and Space Sciences 7 Incentive Program for the Training of Excellence of Young Researchers in Astrophysics and Space Sciences 7 IA-ON 5 8 The IA team (2018) 9 Origin and Evolution of Stars and Planets Group 9 Galaxies, Cosmology, and the Evolution of the Universe Group 10 Instrumentation and Systems Group 11 Interface to Science 11 Research Projects/Programmes 12 Projects focused on scientific activities 12 Projects focused on communication and outreach 15 Scientific Output and Activities 16 Origin and Evolution of Stars and Planets 20 Towards the detection and characterisation of other Earths 21 Towards a comprehensive study of stars 25 Galaxies, Cosmology, and the Evolution of the Universe 30 The assembly history of galaxies resolved in space and time 32 Unveiling the dynamics of the Universe 36 Instrumentation and Systems 39 Space and Ground Systems and Technologies 45 Science Communication 47 The Portuguese ALMA Centre of Expertise 50 Scientific Output 53 Books 53 Published articles 53 Book chapters and Proceedings 59 Book chapters and Proceedings 59 International Scientific Communications 61 National Scientific Communications 65 Organization of Conferences 55 Seminars at IA 66 Organization of Conferences 67 Observing runs 67 Outreach talks 69 4 | IA ACTIVITY REPORT 2018 Reports 72 External seminars by IA researchers 72 PhD completed 73 MSc Projects completed 74 BSc Traineeships/Projects completed 74 2018 IA ACTIVITY REPORT | 5 Unit Overview The Instituto de Astrofísica e Ciências do Espaço (IA) is the reference institution for research in Astronomy, Astrophysics and Space Sciences in Portugal, implementing a bold strategy for the development of this area in the country. -

AMD-Stability and the Classification of Planetary Systems
A&A 605, A72 (2017) DOI: 10.1051/0004-6361/201630022 Astronomy c ESO 2017 Astrophysics& AMD-stability and the classification of planetary systems? J. Laskar and A. C. Petit ASD/IMCCE, CNRS-UMR 8028, Observatoire de Paris, PSL, UPMC, 77 Avenue Denfert-Rochereau, 75014 Paris, France e-mail: [email protected] Received 7 November 2016 / Accepted 23 January 2017 ABSTRACT We present here in full detail the evolution of the angular momentum deficit (AMD) during collisions as it was described in Laskar (2000, Phys. Rev. Lett., 84, 3240). Since then, the AMD has been revealed to be a key parameter for the understanding of the outcome of planetary formation models. We define here the AMD-stability criterion that can be easily verified on a newly discovered planetary system. We show how AMD-stability can be used to establish a classification of the multiplanet systems in order to exhibit the planetary systems that are long-term stable because they are AMD-stable, and those that are AMD-unstable which then require some additional dynamical studies to conclude on their stability. The AMD-stability classification is applied to the 131 multiplanet systems from The Extrasolar Planet Encyclopaedia database for which the orbital elements are sufficiently well known. Key words. chaos – celestial mechanics – planets and satellites: dynamical evolution and stability – planets and satellites: formation – planets and satellites: general 1. Introduction motion resonances (MMR, Wisdom 1980; Deck et al. 2013; Ramos et al. 2015) could justify the Hill-type criteria, but the The increasing number of planetary systems has made it nec- results on the overlap of the MMR island are valid only for close essary to search for a possible classification of these planetary orbits and for short-term stability. -

Exoplanet.Eu Catalog Page 1 Star Distance Star Name Star Mass
exoplanet.eu_catalog star_distance star_name star_mass Planet name mass 1.3 Proxima Centauri 0.120 Proxima Cen b 0.004 1.3 alpha Cen B 0.934 alf Cen B b 0.004 2.3 WISE 0855-0714 WISE 0855-0714 6.000 2.6 Lalande 21185 0.460 Lalande 21185 b 0.012 3.2 eps Eridani 0.830 eps Eridani b 3.090 3.4 Ross 128 0.168 Ross 128 b 0.004 3.6 GJ 15 A 0.375 GJ 15 A b 0.017 3.6 YZ Cet 0.130 YZ Cet d 0.004 3.6 YZ Cet 0.130 YZ Cet c 0.003 3.6 YZ Cet 0.130 YZ Cet b 0.002 3.6 eps Ind A 0.762 eps Ind A b 2.710 3.7 tau Cet 0.783 tau Cet e 0.012 3.7 tau Cet 0.783 tau Cet f 0.012 3.7 tau Cet 0.783 tau Cet h 0.006 3.7 tau Cet 0.783 tau Cet g 0.006 3.8 GJ 273 0.290 GJ 273 b 0.009 3.8 GJ 273 0.290 GJ 273 c 0.004 3.9 Kapteyn's 0.281 Kapteyn's c 0.022 3.9 Kapteyn's 0.281 Kapteyn's b 0.015 4.3 Wolf 1061 0.250 Wolf 1061 d 0.024 4.3 Wolf 1061 0.250 Wolf 1061 c 0.011 4.3 Wolf 1061 0.250 Wolf 1061 b 0.006 4.5 GJ 687 0.413 GJ 687 b 0.058 4.5 GJ 674 0.350 GJ 674 b 0.040 4.7 GJ 876 0.334 GJ 876 b 1.938 4.7 GJ 876 0.334 GJ 876 c 0.856 4.7 GJ 876 0.334 GJ 876 e 0.045 4.7 GJ 876 0.334 GJ 876 d 0.022 4.9 GJ 832 0.450 GJ 832 b 0.689 4.9 GJ 832 0.450 GJ 832 c 0.016 5.9 GJ 570 ABC 0.802 GJ 570 D 42.500 6.0 SIMP0136+0933 SIMP0136+0933 12.700 6.1 HD 20794 0.813 HD 20794 e 0.015 6.1 HD 20794 0.813 HD 20794 d 0.011 6.1 HD 20794 0.813 HD 20794 b 0.009 6.2 GJ 581 0.310 GJ 581 b 0.050 6.2 GJ 581 0.310 GJ 581 c 0.017 6.2 GJ 581 0.310 GJ 581 e 0.006 6.5 GJ 625 0.300 GJ 625 b 0.010 6.6 HD 219134 HD 219134 h 0.280 6.6 HD 219134 HD 219134 e 0.200 6.6 HD 219134 HD 219134 d 0.067 6.6 HD 219134 HD -

Determining the True Mass of Radial-Velocity Exoplanets with Gaia Nine Planet Candidates in the Brown Dwarf Or Stellar Regime and 27 Confirmed Planets? F
A&A 645, A7 (2021) Astronomy https://doi.org/10.1051/0004-6361/202039168 & © F. Kiefer et al. 2020 Astrophysics Determining the true mass of radial-velocity exoplanets with Gaia Nine planet candidates in the brown dwarf or stellar regime and 27 confirmed planets? F. Kiefer1,2, G. Hébrard1,3, A. Lecavelier des Etangs1, E. Martioli1,4, S. Dalal1, and A. Vidal-Madjar1 1 Institut d’Astrophysique de Paris, Sorbonne Université, CNRS, UMR 7095, 98 bis bd Arago, 75014 Paris, France e-mail: [email protected] 2 LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France 3 Observatoire de Haute-Provence, CNRS, Université d’Aix-Marseille, 04870 Saint-Michel-l’Observatoire, France 4 Laboratório Nacional de Astrofísica, Rua Estados Unidos 154, 37504-364, Itajubá - MG, Brazil Received 12 August 2020 / Accepted 24 September 2020 ABSTRACT Mass is one of the most important parameters for determining the true nature of an astronomical object. Yet, many published exoplanets lack a measurement of their true mass, in particular those detected as a result of radial-velocity (RV) variations of their host star. For those examples, only the minimum mass, or m sin i, is known, owing to the insensitivity of RVs to the inclination of the detected orbit compared to the plane of the sky. The mass that is given in databases is generally that of an assumed edge-on system ( 90◦), but many ∼ other inclinations are possible, even extreme values closer to 0◦ (face-on). In such a case, the mass of the published object could be strongly underestimated by up to two orders of magnitude. -

Determining the True Mass of Radial-Velocity Exoplanets with Gaia 9 Planet Candidates in the Brown-Dwarf/Stellar Regime and 27 Confirmed Planets
Astronomy & Astrophysics manuscript no. exoplanet_mass_gaia c ESO 2020 September 30, 2020 Determining the true mass of radial-velocity exoplanets with Gaia 9 planet candidates in the brown-dwarf/stellar regime and 27 confirmed planets F. Kiefer1; 2, G. Hébrard1; 3, A. Lecavelier des Etangs1, E. Martioli1; 4, S. Dalal1, and A. Vidal-Madjar1 1 Institut d’Astrophysique de Paris, Sorbonne Université, CNRS, UMR 7095, 98 bis bd Arago, 75014 Paris, France 2 LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France? 3 Observatoire de Haute-Provence, CNRS, Universiteé d’Aix-Marseille, 04870 Saint-Michel-l’Observatoire, France 4 Laboratório Nacional de Astrofísica, Rua Estados Unidos 154, 37504-364, Itajubá - MG, Brazil Submitted on 2020/08/20 ; Accepted for publication on 2020/09/24 ABSTRACT Mass is one of the most important parameters for determining the true nature of an astronomical object. Yet, many published exoplan- ets lack a measurement of their true mass, in particular those detected thanks to radial velocity (RV) variations of their host star. For those, only the minimum mass, or m sin i, is known, owing to the insensitivity of RVs to the inclination of the detected orbit compared to the plane-of-the-sky. The mass that is given in database is generally that of an assumed edge-on system (∼90◦), but many other inclinations are possible, even extreme values closer to 0◦ (face-on). In such case, the mass of the published object could be strongly underestimated by up to two orders of magnitude. -

Solar System Analogues Among Exoplanetary Systems
Solar System analogues among exoplanetary systems Maria Lomaeva Lund Observatory Lund University ´´ 2016-EXA105 Degree project of 15 higher education credits June 2016 Supervisor: Piero Ranalli Lund Observatory Box 43 SE-221 00 Lund Sweden Populärvetenskaplig sammanfattning Människans intresse för rymden har alltid varit stort. Man har antagit att andra plan- etsystem, om de existerar, ser ut som vårt: med mindre stenplaneter i banor närmast stjärnan och gas- samt isjättar i de yttre banorna. Idag känner man till drygt 2 000 exoplaneter, d.v.s., planeter som kretsar kring andra stjärnor än solen. Man vet även att vissa av dem saknar motsvarighet i solsystemet, t. ex., heta jupitrar (gasjättar som har migrerat inåt och kretsar väldigt nära stjärnan) och superjordar (stenplaneter större än jorden). Därför blir frågan om hur unikt solsystemet är ännu mer intressant, vilket vi försöker ta reda på i det här projektet. Det finns olika sätt att detektera exoplaneter på men två av dem har gett flest resultat: transitmetoden och dopplerspektroskopin. Med transitmetoden mäter man minsknin- gen av en stjärnas ljus när en planet passerar framför den. Den metoden passar bäst för stora planeter med små omloppsbanor. Dopplerspektroskopin använder sig av Doppler effekten som innebär att ljuset utsänt från en stjärna verkar blåare respektive rödare när en stjärna förflyttar sig fram och tillbaka från observatören. Denna rörelse avslöjar att det finns en planet som kretsar kring stjärnan och påverkar den med sin gravita- tion. Dopplerspektroskopin är lämpligast för massiva planeter med små omloppsbanor. Under projektets gång har vi inte bara letat efter solsystemets motsvarigheter utan även studerat planetsystem som är annorlunda. -
![Arxiv:1207.6212V2 [Astro-Ph.GA] 1 Aug 2012](https://docslib.b-cdn.net/cover/8507/arxiv-1207-6212v2-astro-ph-ga-1-aug-2012-3868507.webp)
Arxiv:1207.6212V2 [Astro-Ph.GA] 1 Aug 2012
Draft: Submitted to ApJ Supp. A Preprint typeset using LTEX style emulateapj v. 5/2/11 PRECISE RADIAL VELOCITIES OF 2046 NEARBY FGKM STARS AND 131 STANDARDS1 Carly Chubak2, Geoffrey W. Marcy2, Debra A. Fischer5, Andrew W. Howard2,3, Howard Isaacson2, John Asher Johnson4, Jason T. Wright6,7 (Received; Accepted) Draft: Submitted to ApJ Supp. ABSTRACT We present radial velocities with an accuracy of 0.1 km s−1 for 2046 stars of spectral type F,G,K, and M, based on ∼29000 spectra taken with the Keck I telescope. We also present 131 FGKM standard stars, all of which exhibit constant radial velocity for at least 10 years, with an RMS less than 0.03 km s−1. All velocities are measured relative to the solar system barycenter. Spectra of the Sun and of asteroids pin the zero-point of our velocities, yielding a velocity accuracy of 0.01 km s−1for G2V stars. This velocity zero-point agrees within 0.01 km s−1 with the zero-points carefully determined by Nidever et al. (2002) and Latham et al. (2002). For reference we compute the differences in velocity zero-points between our velocities and standard stars of the IAU, the Harvard-Smithsonian Center for Astrophysics, and l’Observatoire de Geneve, finding agreement with all of them at the level of 0.1 km s−1. But our radial velocities (and those of all other groups) contain no corrections for convective blueshift or gravitational redshifts (except for G2V stars), leaving them vulnerable to systematic errors of ∼0.2 km s−1 for K dwarfs and ∼0.3 km s−1 for M dwarfs due to subphotospheric convection, for which we offer velocity corrections. -

On the Mass Estimation for FGK Stars: Comparison of Several Methods
Mon. Not. R. Astron. Soc. 000, 1–?? (2002) Printed 29 August 2014 (MN LATEX style file v2.2) On the mass estimation for FGK stars: comparison of several methods F. J. G. Pinheiro1,2⋆, J. M. Fernandes1,2,3, M. S. Cunha4,5, M. J. P. F. G. Monteiro4,5,6, N. C. Santos4,5,6, S. G. Sousa4,5,6, J. P. Marques7, J.-J. Fang8, A. Mortier9 and J. Sousa4,5 1Centro de Geofísica da Universidade de Coimbra 2Observatório Geofísico e Astronómico da Universidade de Coimbra 3Departamento de Matemática da Universidade de Coimbra, Largo D. Dinis, P-3001-454 Coimbra, Portugal 4Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, PT4150-762 Porto, Portugal 5Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal 6Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Portugal 7The Institut d’Astrophysique Spatiale, Orsay, France 8Centro de Física Computacional, Department of Physics, University of Coimbra, P-3004-516 Coimbra, Portugal 9SUPA, School of Physics and Astronomy, University of St Andrews, St Andrews KY16 9SS, UK Accepted . Received ABSTRACT Stellar evolutionary models simulate well binary stars when individual stellar mass and system metallicity are known. The mass can be derived directly from observations only in the case of multiple stellar systems, mainly binaries. Yet the number of such stars for which ls accurate stellar masses are available is rather small. The main goal of this project is to provide realistic mass estimates for an homogeneous sample of about a thousand FGK single stars, using four different methods and techniques. -

Properties of Members of Stellar Kinematic Groups and Stars with Circumstellar Dusty Debris Discs
UNIVERSIDAD AUTONOMA´ DE MADRID Facultad de Ciencias Departamento de F´ısica Teorica´ A spectroscopic study of the nearby late-type stellar population: Properties of members of stellar kinematic groups and stars with circumstellar dusty debris discs. PhD dissertation submitted by Jesus´ Maldonado Prado for the degree of Doctor in Physics Supervised by Dr. Carlos Eiroa de San Francisco Madrid, June 2012 UNIVERSIDAD AUTONOMA´ DE MADRID Facultad de Ciencias Departamento de F´ısica Teorica´ Estudio espectroscopico´ de la poblacion´ estelar fr´ıa cercana: Propiedades de estrellas en grupos cinematicos´ estelares y de estrellas con discos circunestelares de tipo debris. Memoria de tesis doctoral presentada por Jesus´ Maldonado Prado para optar al grado de Doctor en Ciencias F´ısicas Trabajo dirigido por el Dr. Carlos Eiroa de San Francisco Madrid, Junio de 2012 A mis padres y hermanos Agradecimientos La finalizaci´on de una tesis doctoral es siempre un momento para el balance y la reflexi´on. Conf´ıo que estas breves palabras sirvan de peque˜no reconocimiento a todas las personas que durante todo este largo, y no siempre f´acil, per´ıodo de tiempo han tenido a bien brindarme su ayuda, su apoyo y, en muchos casos, su simpat´ıa. A todos los que de alguna manera me habe´ıs ayudado, gracias. Las primeras palabras de estas notas deben ser para mi supervisor de tesis, Carlos Eiroa, por su confianza, su apoyo y dedicaci´on y sobre todo por esa mi- rada cr´ıtica tan suya que, desde siempre, ha tratado de transmitirme. A Benjam´ın Montesinos debo agradecerle muchas cosas, en particular su cercan´ıa y su forma de ser, a David Montes y a Raquel Mart´ınez, su esfuerzo y dedicaci´on. -

Predictions of Planets for 586 Exosystems and a Method for Predicting Planets in Multi-Planetary Exosystems Valeri Beck
Predictions of planets for 586 exosystems and a method for predicting planets in multi-planetary exosystems Valeri Beck To cite this version: Valeri Beck. Predictions of planets for 586 exosystems and a method for predicting planets in multi- planetary exosystems. 2019. hal-02050412v4 HAL Id: hal-02050412 https://hal.archives-ouvertes.fr/hal-02050412v4 Preprint submitted on 7 Aug 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Predictions of planets for 586 exosystems and a method for predicting planets in multi-planetary exosystems Valeri Beck*1 *Alfa Carbon® Beck, Berlin, Germany ABSTRACT We have applied a model of planetary system formation in the field of a standing sound wave (the ‘SSW-Model’) to the prediction of planets in 586 multi-planetary exosystems (384 bi- planetary, 127 tri-planetary and 75 exosystems with four or more confirmed planets). We have verified our predictions using transit-like events from the NASA Threshold-Crossing Event (TCE) catalogue, finding that more than 80% of these events are included in our list of exoplanet predictions. We describe a method for predicting the periods and semi-major axes of additional planets for exosystems with two or more confirmed planets.