Investigation of Using Solar Energy: a Case Study
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PROTESTS and REGIME SUPPRESSION in POST-REVOLUTIONARY IRAN Saeid Golkar
THE WASHINGTON INSTITUTE FOR NEAR EAST POLICY n OCTOBER 2020 n PN85 PROTESTS AND REGIME SUPPRESSION IN POST-REVOLUTIONARY IRAN Saeid Golkar Green Movement members tangle with Basij and police forces, 2009. he nationwide protests that engulfed Iran in late 2019 were ostensibly a response to a 50 percent gasoline price hike enacted by the administration of President Hassan Rouhani.1 But in little time, complaints Textended to a broader critique of the leadership. Moreover, beyond the specific reasons for the protests, they appeared to reveal a deeper reality about Iran, both before and since the 1979 emergence of the Islamic Republic: its character as an inherently “revolutionary country” and a “movement society.”2 Since its formation, the Islamic Republic has seen multiple cycles of protest and revolt, ranging from ethnic movements in the early 1980s to urban riots in the early 1990s, student unrest spanning 1999–2003, the Green Movement response to the 2009 election, and upheaval in December 2017–January 2018. The last of these instances, like the current round, began with a focus on economic dissatisfaction and then spread to broader issues. All these movements were put down by the regime with characteristic brutality. © 2020 THE WASHINGTON INSTITUTE FOR NEAR EAST POLICY. ALL RIGHTS RESERVED. SAEID GOLKAR In tracking and comparing protest dynamics and market deregulation, currency devaluation, and the regime responses since 1979, this study reveals that cutting of subsidies. These policies, however, spurred unrest has become more significant in scale, as well massive inflation, greater inequality, and a spate of as more secularized and violent. -

Future Strategies for Promoting Tourism and Petroleum Heritage in Khuzestan Province, Iran
Future strategies for promoting tourism and petroleum heritage in Khuzestan Province, Iran Sahar Amirkhani, Neda Torabi Farsani and Homa Moazzen Jamshidi Abstract Sahar Amirkhani and Purpose – Industrial tourism not only strives to preserve industrial heritage, but can also be a strategy for being Neda Torabi Farsani are both familiar with the history of industry and attracting tourists to new destinations. This paper examines the issue of based at the Department of promoting petroleum industrial tourism in the case of Khuzestan, Iran. The research aims at determining Museum and Tourism, Art appropriate strategies for promoting petroleum industrial tourism. University of Isfahan, – Design/methodology/approach The data were analysed through a strengths, weaknesses, opportunities, Isfahan, Iran. and threats (SWOT) model. Homa Moazzen Jamshidi is Findings – The results revealed the competitive strategy as the best. Lastly, strategies such as: concentric based at the Department of diversification, joint venture strategy, conglomerate diversification and horizontal diversification were proposed Economics and Arts as key solutions. The results support the view that establishing an exploratory ecomuseum in the territory of Entrepreneurship, Art Khuzestan Province can be a suitable concentric diversification strategy towards petroleum industrial sustainable tourism in the future. University of Isfahan, Originality/value – The main originality of this paper includes linking tourism with the petroleum (oil and natural Isfahan, Iran. gas) industry -

Iran's Global Petroleumscape: the Role of Oil in Shaping Khuzestan and Tehran
Delft University of Technology Iran’s Global Petroleumscape The Role of Oil in Shaping Khuzestan and Tehran Hein, Carola; Sedighi, Mo DOI 10.1080/13264826.2018.1379110 Publication date 2017 Document Version Final published version Published in Architectural Theory Review (online) Citation (APA) Hein, C., & Sedighi, M. (2017). Iran’s Global Petroleumscape: The Role of Oil in Shaping Khuzestan and Tehran. Architectural Theory Review (online), 21(3), 349-374. https://doi.org/10.1080/13264826.2018.1379110 Important note To cite this publication, please use the final published version (if applicable). Please check the document version above. Copyright Other than for strictly personal use, it is not permitted to download, forward or distribute the text or part of it, without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license such as Creative Commons. Takedown policy Please contact us and provide details if you believe this document breaches copyrights. We will remove access to the work immediately and investigate your claim. This work is downloaded from Delft University of Technology. For technical reasons the number of authors shown on this cover page is limited to a maximum of 10. Article IRAN’S GLOBAL PETROLEUMSCAPE: THE ROLE OF OIL IN SHAPING KHUZESTAN AND TEHRAN Carola Hein Delft University of Technology Email: [email protected] Mohamad Sedighi Delft University of Technology Email: [email protected] Various constellations of oil actors—including corporations and nations—have shaped seemingly disconnected and geographically distant landscapes, cities, and buildings around the world over the last 150 years. -
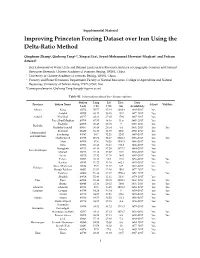
Improving Princeton Forcing Dataset Over Iran Using the Delta-Ratio Method
Supplemental Material Improving Princeton Forcing Dataset over Iran Using the Delta-Ratio Method Qinghuan Zhang1, Qiuhong Tang1,2*, Xingcai Liu1, Seyed-Mohammad Hosseini-Moghari1 and Pedram Attarod3 1 Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing, 100101, China 2 University of Chinese Academy of Sciences, Beijing, 100101, China 3 Forestry and Forest Economics Department, Faculty of Natural Resources, College of Agriculture and Natural Resources, University of Tehran, Karaj, 77871-31587, Iran *Correspondence to: Qiuhong Tang ([email protected]) Table S1. Information about the climate stations. Station Long Lat Elev. Data Province Station Name Adjust Validate Code (° E) (° N) (m) Availability Alborz Karaj 40752 50.57 35.48 1292.9 1985–2017 Yes Ardebil 40708 48.17 38.15 1332 1977–2017 Yes Ardebil Khalkhal 40717 48.31 37.38 1796 1987–2017 Yes Pars Abad Moghan 40700 47.55 39.39 31.9 1985–2017 Yes Bushehr 40858 50.49 28.58 9 1986–2017 Yes Bushehr Bushehr Coastal 40857 50.49 28.54 8.4 1951–2017 Yes Yes Boroojen 99459 51.18 31.59 2260 1988–2017 Yes Chaharmahal Koohrang 40797 50.7 32.26 2285 1987–2017 Yes and Bakhtiari Shahre Kord 40798 50.51 32.17 2048.9 1956–2017 Yes Yes Ahar 40704 47.4 38.26 1390.5 1986–2017 Yes Jolfa 40702 45.40 38.45 736.2 1986–2017 Yes Maragheh 40713 46.16 37.24 1477.7 1984–2017 Yes East Azarbaijan Mianeh 40716 47.42 37.27 1110 1987–2017 Yes Sarab 40710 47.32 37.56 1682 1987–2017 Yes Tabriz 40706 46.17 -

Iraq Situation Sources: UNHCR Field Office UNHCR, Global Insight Digital Mapping Elevation © 1998 Europa Technologies Ltd
FF II CC SS SS Capital Armistice Demarcation Line Field Information and Administrative boundary Coordination Support Section UNHCR Representation Main road Division of Operational Services UNHCR Sub office Railway Iraq Situation Sources: UNHCR Field office UNHCR, Global Insight digital mapping Elevation © 1998 Europa Technologies Ltd. UNHCR Presence (Above mean sea level) MoDM, IOM, IDP Working Group C Refugee settlement As of April 2008 3,250 to 4,000 metres Refugee camp 2,500 to 3,250 metres The boundaries and names shown and the designations used on this Town or village of interest 1,750 to 2,500 metres map do not imply official endorsement 1,000 to 1,750 metres Exclusively for internal UNHCR use !! Main town or village or acceptance by the United Nations. 750 to 1,000 metres ((( Secondary town or village Iraq_SituationMapEthnoGroups_A3LC.WOR ((( ((( ((( 500 to 750 metres ((( Andirin !! ((( ((( ((( ((( Hakkâri ((( Yüksekova Kahramanmaras((( ((( ((( Gercus !! ((( ((( !! ((( ((( Kuyulu ((( Savur International boundary ((( Pazarcik((( Golcuk ((( !! 250 to 500 metres ((( !! ((( ((( !! ((( ((( !! ((( ((( !! ((( Bandar-e Anzali !! ((( !! ((( Karakeci OrumiyehOrumiyeh ((( Kozan ((( ((( OrumiyehOrumiyeh ((( Meyaneh ((( ((( ((( ((( !! ((( !! Turkoglu((( Yaylak((( ((( ((( !! Maraghen ((( Boundary of former Kadirli((( !! ((( Akziyaret ((( Derik ((( ((( ((( 0 to 250 metres ((( ((( (((Cizre ((( Bonab !! ((( ((( !! !! ((( ((( ( ((( Mardin Sume`eh Sara !! ((( Kuchesfahan ( ((( ((( ((( ((( SilopiSilopi !! Palestine Mandate Karaisali((( -

Agroclimatic Zones Map of Iran Explanatory Notes
AGROCLIMATIC ZONES MAP OF IRAN EXPLANATORY NOTES E. De Pauw1, A. Ghaffari2, V. Ghasemi3 1 Agroclimatologist/ Research Project Manager, International Center for Agricultural Research in the Dry Areas (ICARDA), Aleppo Syria 2 Director-General, Drylands Agricultural Research Institute (DARI), Maragheh, Iran 3 Head of GIS/RS Department, Soil and Water Research Institute (SWRI), Tehran, Iran INTRODUCTION The agroclimatic zones map of Iran has been produced to as one of the outputs of the joint DARI-ICARDA project “Agroecological Zoning of Iran”. The objective of this project is to develop an agroecological zones framework for targeting germplasm to specific environments, formulating land use and land management recommendations, and assisting development planning. In view of the very diverse climates in this part of Iran, an agroclimatic zones map is of vital importance to achieve this objective. METHODOLOGY Spatial interpolation A database was established of point climatic data covering monthly averages of precipitation and temperature for the main stations in Iran, covering the period 1973-1998 (Appendix 1, Tables 2-3). These quality-controlled data were obtained from the Organization of Meteorology, based in Tehran. From Iran 126 stations were accepted with a precipitation record length of at least 20 years, and 590 stations with a temperature record length of at least 5 years. The database also included some precipitation and temperature data from neighboring countries, leading to a total database of 244 precipitation stations and 627 temperature stations. The ‘thin-plate smoothing spline’ method of Hutchinson (1995), as implemented in the ANUSPLIN software (Hutchinson, 2000), was used to convert this point database into ‘climate surfaces’. -

S 22863-EN.Pdf
UNITED NATIONS S Distr. GENERAL S/22863 31 July 1991 ORIGINAL: ENGLISH LETTER DATED 31 JULY 1991 FROM THE SECRETARY-GENERAL ADDRESSED TO THE PRESIDENT OF THE SECURITY COUNCIL I wish to refer to my letter of 23 May (S/22637) in which I informed you that in pursuance of the mandate entrusted to me by paragraph 7 of resolution 598 (19871, I had asked former Under-Secretary-General Mr. Abdulrahim A. Farah to lead a team of experts to make an exploratory visit to the Islamic Republic of Iran for the purpose stated therein. The team visited the Islamic Republic of Iran from 31 May to 21 June 1991. The preliminary report of the mission containing details of the reported damage to the country's infrastructure, the nature and status of the country* 's reconstruction efforts and the team's observations on the damaged sites and installations inspected is submitted herewith for the information of members of the Security Council. The team will return to the Islamic Republic of Iran in the near future to complete its work. (Signed) Javier PEREZ de CUELLAR 91-23907 2511.-12h (I?) / . 5122863 English Page 3 Annex PRELIMINARY REPORT OF A UNITED NATIONS TEAM, APPOINTED BY THE SECRETARY-GENERAL IN ACCORDANCE WITH SECURITY COUNCIL RESOLUTION 598 (1987), PARAGRAPH 7, TO OBTAIN INITJAL INFORMATION AND DATA ON THE NATURE AND EXTENT OF THE DAMAGE SUSTAINED BY THE ISLAMIC REPUBLIC OF IRAN AS A RESULT OF THE CONFLICT BETWEEN THE ISLAMIC REPUBLIC OF IRAN AND IRAQ, AND ON THE STATUS OF THE FORMER'S RECONSTRUCTION EFFORTS 31 MAY 1991-21 JUNE 1991 / . -
Iraq and Neighbouring Countries Geographic Information and Mapping Unit Population and Geographic Data Section As of November 2003 Email : [email protected]
GIMU / PGDS Iraq and neighbouring countries Geographic Information and Mapping Unit Population and Geographic Data Section As of November 2003 Email : [email protected] Haymana )))) )))) )))) )))) )))) Goradiz ))) )))) Akpinar )))) )))) Tecer )))) Sincan )))) ))) Bank ))) Cheleken )))) )))) )))) ))) ))) )))) )))) )))) Akbenli )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) ))) )))) )))) )))) )))) Sarkisla )))) )))) Hinis ))) Neftechala )))) )))) )))) )))) ))) Karacaoren )))) )))) )))) 33° E 34° E 35° E 36° E )))) 37° E 38° E 39° E 40° E 41° E 42° E 43° E 44° E 45° E 46° E 47° E 48° E 49° E 50° E 51° E 52° E 53° E )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) Uzunlu)))) )))) )))) )))) )))) Caylar )))) )))) )))) )))) Kangal )))) )))) )))) )))) )))) )))) )))) )))) ))) )))) )))) )))) Karaoglan Nakhichevan' ))) ))) ))) )))) )))) )))) )))) ))) ))) Dzhalilabad )))) )))) )))) )))) ))) )))) )))) )))) UU ))) )))) Seker )))) Varto )))) UU ))) ))) )))) )))) UU ))) ))) )))) )))) UU ))) ))) )))) UU ))) ))) )))) UU ))) ))) )))) )))) UU ))) ))) Kirsehir )))) )))) )))) )))) )))) Kadzharan ))) )))) )))) )))) )))) )))) )))) )))) )))) ))) Prishib )))) )))) )))) )))) Hozat)))) Tunceli )))) Sancak )))) ))) )))) )))) )))) )))) )))) )))) )))) )))) ))) )))) )))) )))) )))) )))) Bulanik Paraga ))) )))) )))) )))) Horan )))) )))) )))) )))) )))) Arapkir )))) )))) )))) )))) ))) )))) )))) )))) Ercis )))) )))) ))) Masally )))) )))) )))) )))) 39° N )))) )))) )))) )))) )))) )))) ))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) )))) -

Pharmaceutical Sciences
IAJPS 2018, 05 (01), 161-168 Farideh Pargar et al ISSN 2349-7750 CODEN [USA]: IAJPBB ISSN: 2349-7750 INDO AMERICAN JOURNAL OF PHARMACEUTICAL SCIENCES Available online at: http://www.iajps.com Research Article ASSESSMENT OF THE PREPAREDNESS OF ALL AHWAZ MEDICAL CENTERS IN THE FACE OF THE CRISIS IN 2017 Farideh Pargar1*, Khaled Biet saeed2, Ayat Alah ebadi3, Sedighe Ghobadian4, Mohammad Adineh5 1M.Sc Midwifery, Applied Research Center of Police Medicine, Department of Health, Rescue and Treatment, Police force, Tehran ,iran 2 Ph.D Strategic Management Student, Applied Research Center of Police Medicine, Department of Health, Rescue and Treatment, Police Force, Tehran, Iran 3 General Practitioner, Applied Research Center of Police Medicine, Department of Health, Rescue and Treatment, Police Force, Tehran, Iran 4 M.Sc Hospital Management, Applied Research Center of Police Medicine, Department of Health, Rescue and Treatment, Police Force, Tehran, Iran 5 Nursing care Research Center in Chronic Diseases, School of Nursing and Midwifery, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran. Abstract: Accidents and disasters are sudden and sometimes catastrophic events that disrupt the pattern of life of people in society and, hospitals are among the first units that can play a vital role in saving the injured. In this study, the preparedness of all Ahwaz medical centers in dealing with the crisis in 2017 was investigated. Materials and method: This research is a descriptive study. The research tool is a Hospital Preparedness Assessment Questionnaire, which has 9 key components of command control, triage, human resource, communication, capacity building, support and logistics management, safety and security, continuity of critical services and post-disaster recovery. -

Salinity Management in Iran
Chapter 1. Present status of salt-affected and waterlogged soils in Dasht-e-Azadegan and management strategies for their sustainable utilization S.A.M. Cheraghi1*, N. Heydari2, Y. Hasheminejad1, M. Qadir3, H. Farahani3, and T. Oweis3 1National Salinity Research Center (NSRC), Yazd, Iran; 2Iranian Agricultural Engineering Research Institute, Karaj, Iran; 3International Center for Agricultural Research in the Dry Areas (ICARDA), Aleppo, Syria *Corresponding author: [email protected] 1 Introduction southwest Iran is potentially one of the most suitable regions for agricultural Salt-prone land and water resources production. However, salinization of are major impediments to the optimal land and water resources has become a utilization of crop production systems serious threat to efficient use of these in many arid and semi-arid regions of invaluable resources. It is estimated the world, including Iran (Alizadeh et that out of the total 6.7 Mha of the al. 2004; Moghaddam and Koocheki province, 1.2-1.5 Mha (18-22% of total 2004). The salinization of land and water area) are faced with the dual problems resources has been the consequence of of soil salinization and water logging both anthropogenic activities (causing (Anonymous 2000). human-induced or secondary salinity and/or sodicity) and naturally occurring The Karkheh river basin (KRB) is one of phenomena (causing primary fossil the major river basins in the Khuzestan salinity and/or sodicity) (Ghassemi et al. province, consisting of two main sub- 1995). The main cropping systems in the basins namely Karkheh Olia (upstream) country are based on irrigated agriculture and Karkheh Sofla (downstream). The where at least 50% area (4.1 Mha) fall KRB is, most notably, the eastern flank under different types of salt-affected of the ‘cradle of civilization’ (ancient soils (Cheraghi 2004). -

Study on Geomorphologic Dynamics of Limestone-Shale Collapse in The
The 1 st International Applied Geological Congress, Department of Geology, Islamic Azad University - Mashad Branch, Iran, 26-28 April 2010 Study on geomorphology dynamics of limestone-shale collapse in the Kollah-Ghazy Area, south Esfahan, Iran A.Vali,R.Ghazavi,R.Ghasemi, A.behpouri Faculty members in agriculture and Natural Resources College of Darab.Shiraz University. Corresponding author: [email protected] Abstract The focus of geomorphology is concerned with an analysis of the nature, arrangement and differentiation of landforms and an understanding of the processes that have shaped or are shaping those landforms. Uplift at the end of Cretaceous and beginning of the Tertiary created asymmetric domes. Foresets of limestone and shale in stratigraphic units of Shear folding area to Cretaceous in the Kollah-Ghazy of south and south-east of Esfahan have resulted in many collapse features that have developed several shapes like cuesta. Erosion of these uplifted rocks produced the present landscape .resistant sandstone that are ordered near the shale layer has been formed the cuesta like form .Results of morphology showed in spite of these forms lay in folded structure, they have any characteristics that they have contained in monoclimb structures such as foresets of hard and weak layers with temperate slope in construction simple and agreeable limb. In this paper we have tried to investigate the relationship between slope particulars and speed of destruction and layer dynamics, with measuring some geomorphology quantitative parameters. Analysis of regression showed a significant relationship between slope of weak layers with slope and thickness of hard layers. Also the slope of weak layer desire to angle of repose because of weathering effects, gravity and friction forces. -

EPPO Bulletin E-Mail to Hq@Eppo
Entomology and Applied Science Letters Volume 6, Issue 3, Page No: 73-81 Copyright CC BY-NC-ND 4.0 Available Online at: www.easletters.com ISSN No: 2349-2864 Epidemiologic - Demographic Status of Scorpion- Stung Patients in Khorramshahr County, Southwestern Iran Hamid Kassiri1*, Iman Khodkar2, Shahnaz Kazemi 3, Niusha Kasiri 2, Maral Kasiri4 1 Department of Medical Entomology, School of Health, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran. 2 Student Research Committee, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran 3 Khorramshahr County Health Center, Abadan School of Medical Sciences, Abadan, Iran. 4 Department of Biomedical Engineering, University of Southern California, Los Angeles, California, United States of America. ABSTRACT Introduction and Objectives: Nearly two-thousand scorpion species have been identified worldwide, twenty-five of which have health importance. Each year approximately half a million individuals are stung by scorpions in the world with a fatality rate of 3250 people. In Iran, there are nearly 40000 cases in a year and the numbers of recorded deaths are between 14-29 people. Scorpionism is one of the most significant medical subjects in Iran especially in the southern areas; so that Khuzestan Province is one of the most significant foci of scorpionism. Therefore, the present study aimed to determine the epidemiological characteristics of the individuals stung by scorpions in Khorramshahr region, Khuzestan province, Southwestern Iran. Materials and Methods: In this analytic descriptive study, all patients with scorpion sting were assessed from 2013 to 2017. Data regarding the patient's age, gender, site of the sting, month of envenomation, administration of scorpion antivenin, time of the sting, geographical area, and the color of scorpion were extracted and recorded.