Assessment of the Impact of Climate Variability and Change on the Reliability, Resiliency and Vulnerability of Complex Flood Protection Systems Project No
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Morning Conditions Report Assiniboine River
Hydrologic Forecasting and Water Management July 22, 2020 Morning Conditions Report PROVISIONAL DATA http://www.gov.mb.ca/mit/floodinfo Assiniboine River - Tributaries Map Today's Conditions Change Today's Conditions Change ID LOCATION (Imperial) from (Metric) from Jul 21 Jul 21 FLOW LEVEL FLOW LEVEL (m) (cfs) (ft) (ft) (cms) (m) 1 Conjuring Creek near Russell 3 1,813.79 +0.03 0.1 552.84 +0.01 2 Smith Creek near Marchwell 0 1.22 -0.03 0.0 0.37 -0.01 3 Silver Creek near Binscarth 4 Cutarm Creek near Spy Hill 5 3.98 -0.01 0.1 1.21 0.00 5 Scissor Creek near Mcauley 2 2.96 +0.01 0.1 0.90 0.00 6 Birdtail Creek near Birtle 46 1,588.85 +0.22 1.3 484.28 +0.07 7 Arrow River near Arrow River 11 331.58 -0.03 0.3 101.07 -0.01 8 Gopher Creek near Virden 1 2.10 +0.06 0.0 0.64 +0.02 9 Oak River near Rivers 136 3.53 -0.05 3.8 1.08 -0.01 10 Baileys Creek near Oak Lake 0 337.50 -0.07 0.0 102.87 -0.02 11 Rolling River near Erickson 263 1,993.57 -0.11 7.4 607.64 -0.03 12 Little Saskatchewan River near Horod 102 26.76 -0.03 2.9 8.16 -0.01 13 Little Saskatchewan River near Minnedosa 512 1,715.84 -0.18 14.5 522.99 -0.05 14 Minnedosa Lake 1,682.47 +0.08 512.82 +0.02 15 Little Saskatchewan River above Rapid City Dam** 16 Rivers Reservoir* 1,538.18 -0.14 468.84 -0.04 17 Little Saskatchewan River near Rivers 1,819 1,484.00 -0.17 51.5 452.32 -0.05 18 Little Souris River near Brandon 19 4.96 -0.03 0.5 1.51 -0.01 19 Epinette Creek near Carberry 13 1.41 -0.01 0.4 0.43 0.00 20 Cypress River near Bruxelles 50 329.85 +0.64 1.4 100.54 +0.19 21 Sturgeon Creek at St. -

Flood Fighting in Manitoba
Flood Fighting in Manitoba A History and Background of Manitoba’s Flood Protection Works Flood Fighting in Manitoba Southern Manitoba has extensive flood control Flood protection work has prevented property measures in place, particularly in the Red River damage and reduced the potential impact of Valley, from Winnipeg, south to the US border. flooding on families and communities. Since Flood controls were built after the devastating flood the 1997 flood, more than $1 billion has been of 1950, which flooded the Red River Valley and invested in flood mitigation efforts in Manitoba. the City of Winnipeg. Construction of the Red River This investment has prevented over $7 billion in Floodway was completed in 1968. Additional flood damages throughout Manitoba. control improvements, including an expansion of the The 2011 flood affected a large geographic floodway, were made after the Flood of the area and thousands of Manitobans. Early flood Century in 1997. This flood was substantially larger forecasts and flood-mitigation efforts helped many than the 1950 flood, but resulted in far less property communities get a head start on protecting homes damage because of the flood control measures in and lands, but damage was still widespread. place. There are also flood control measures along the Assiniboine River. Flood Control Infrastructure in Southern Manitoba DauDpahuinp hRiniv Reriver ! ! LakLeake FirsFt iNrsat tNioantion WaWterahteernhen WinWninipneigpoesgiossis LakLea kSet. SMta. rMtianrtin RivReriver DikDesikes " W"aWtearhteernhen LakLea kSet. SMta. rMtianrtin DuDcuk ck DikDesikes LittLleit tSlea sSkaastkcahtecwhaenwan " " EmEemrgeerngceyn Ccyh aCnhnaenlnel MoMuonutanitna in DikDesikes " " ProPvr.o Pv.a Prkark FairFfoairrdford LaLkeake MoMssoeyssey FirsFt iNrsat tNioanti!on !St.S Mt. -

Geomorphic and Sedimentological History of the Central Lake Agassiz Basin
Electronic Capture, 2008 The PDF file from which this document was printed was generated by scanning an original copy of the publication. Because the capture method used was 'Searchable Image (Exact)', it was not possible to proofread the resulting file to remove errors resulting from the capture process. Users should therefore verify critical information in an original copy of the publication. Recommended citation: J.T. Teller, L.H. Thorleifson, G. Matile and W.C. Brisbin, 1996. Sedimentology, Geomorphology and History of the Central Lake Agassiz Basin Field Trip Guidebook B2; Geological Association of CanadalMineralogical Association of Canada Annual Meeting, Winnipeg, Manitoba, May 27-29, 1996. © 1996: This book, orportions ofit, may not be reproduced in any form without written permission ofthe Geological Association ofCanada, Winnipeg Section. Additional copies can be purchased from the Geological Association of Canada, Winnipeg Section. Details are given on the back cover. SEDIMENTOLOGY, GEOMORPHOLOGY, AND HISTORY OF THE CENTRAL LAKE AGASSIZ BASIN TABLE OF CONTENTS The Winnipeg Area 1 General Introduction to Lake Agassiz 4 DAY 1: Winnipeg to Delta Marsh Field Station 6 STOP 1: Delta Marsh Field Station. ...................... .. 10 DAY2: Delta Marsh Field Station to Brandon to Bruxelles, Return En Route to Next Stop 14 STOP 2: Campbell Beach Ridge at Arden 14 En Route to Next Stop 18 STOP 3: Distal Sediments of Assiniboine Fan-Delta 18 En Route to Next Stop 19 STOP 4: Flood Gravels at Head of Assiniboine Fan-Delta 24 En Route to Next Stop 24 STOP 5: Stott Buffalo Jump and Assiniboine Spillway - LUNCH 28 En Route to Next Stop 28 STOP 6: Spruce Woods 29 En Route to Next Stop 31 STOP 7: Bruxelles Glaciotectonic Cut 34 STOP 8: Pembina Spillway View 34 DAY 3: Delta Marsh Field Station to Latimer Gully to Winnipeg En Route to Next Stop 36 STOP 9: Distal Fan Sediment , 36 STOP 10: Valley Fill Sediments (Latimer Gully) 36 STOP 11: Deep Basin Landforms of Lake Agassiz 42 References Cited 49 Appendix "Review of Lake Agassiz history" (L.H. -

Water Quality Report
Central Assiniboine Watershed Integrated Watershed Management Plan - Water Quality Report October 2010 Central Assiniboine Watershed – Water Quality Report Water Quality Investigations and Routine Monitoring: This report provides an overview of the studies and routine monitoring which have been undertaken by Manitoba Water Stewardship’s Water Quality Management Section within the Central Assiniboine watershed. There are six long term water quality monitoring stations (1965 – 2009) within the Central Assiniboine Watershed. These include the Assiniboine, Souris and Cypress Rivers. There are also ten stations not part of the long term water quality monitoring program in which some data are available for alternate locations on the Assiniboine, Souris, and Little Saskatchewan Rivers. The Central Assiniboine River watershed area is characterized primarily by agricultural crop land, industry, urban and rural centres. All these land uses have the potential to negatively impact water quality, if not managed appropriately. Cropland can present water quality concerns in terms of fertilizer and pesticide runoff entering surface water. There are a number of large industrial operations in the Central Assiniboine Watershed, these present water quality concerns in terms of wastewater effluent and industrial runoff. Large centers and rural municipalities present water quality concerns in terms of wastewater treatment and effluent. The tributary of most concern in the Central Assiniboine watershed is the Assiniboine River, as it is the largest river in the watershed. The area surrounding the Assiniboine River is primarily agricultural production yielding a high potential for nutrient and bacteria loading. The Assiniboine River serves as the main drinking water source for many residents in this watershed. In addition, the Assiniboine River drains into Lake Winnipeg, and as such has been listed as a vulnerable water body in the Nutrient Management Regulation under the Water Protection Act. -

Red River Floodway Operation Report Spring 2019
RED RIVER FLOODWAY OPERATION REPORT SPRING 2019 June 28, 2019 Manitoba Infrastructure Hydrologic Forecasting and Water Management Branch Water Management and Structures Division Printed on Recycled Paper EXECUTIVE SUMMARY The 2019 Red River spring flood resulted from above normal to well above normal winter snow fall in the upper Red River basin, including significant late season snowfall in the Fargo area, combined with normal soil moisture going into freeze-up in the fall. The March Outlook published by Manitoba’s Hydrologic Forecast Center estimated that the peak flow at Emerson could exceed the flow seen in the 2011 flood under favorable conditions, and exceed the 2009 flood under normal conditions. Under unfavorable conditions, the 2019 flow at Emerson was forecast to be second only to 1997 in the last 60 years of records. The observed peak at Emerson for the 2019 spring flood was approximately 60,700 cfs (1720.0 m3/s), and occurred on April 25. This is similar to the peak flow observed at Emerson in 2010. The 2019 peak flow measured at Emerson equated to a 1:15 year flood. However, due to the small contributions of tributaries in the lower portion of the basin, the peak natural flood flow at James Avenue only equated to a 1:6 year flood. The 2019 Red River spring flood was driven primarily by significant winter precipitation in the upper portion of the basin, and most of the tributaries on the Canadian side of the border had peaked long before the flood crest arrived. Ice was not a major concern on the Red or Assiniboine rivers in 2019, however, some ice jamming did occur north of the City of Winnipeg in the Selkirk and Netley Creek areas. -

Manitoba's Flood of 2011
Manitoba’s Flood of 2011 • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • Steve Topping, P. Eng Executive Director, Regulatory and Operational Services Manitoba Water Stewardship September 13 , 2011 why was there so much water this year? why this flood was so different than 1997? was this a record-breaking year? Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth •2010 was the 5th wettest September through February on record following the first wettest on record (2009) and 3rd wettest (2010). October 26-28th 2010 Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography Snow Pack 2011 •Snowfall totals 75 to 90 inches, nearly double the climatological average. Newdale: 6-7 ft snow depth Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography • Precipitation this Spring Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography • Precipitation this Spring • Storm events at the wrong time •15th year of current wet cycle, resulting in very little storage in the soils Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography • Precipitation this Spring • Storm events at the wrong time • Many watersheds flooding simultaneously May Sun Mon Tues Wed Thurs Fri Sat 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Pre-Flood Preparation • Supplies and Equipment • 3 amphibex icebreakers • 7 ice cutting machines • 3 amphibious ATVs • 3 million sandbags • 30,000 super sandbags • 3 sandbagging units (total of 6) • 24 heavy duty steamers (total of 61) • 43 km of cage barriers • 21 mobile pumps (total of 26) • 72 km of water filled barriers • and much more... -

Executive Summary
Page 1 of 26 Hydrologic Forecast Centre Manitoba Infrastructure Winnipeg, Manitoba FEBRUARY FLOOD OUTLOOK February 26, 2021 Executive Summary The February Flood Outlook prepared by the Hydrologic Forecast Centre of Manitoba Infrastructure reports the risk of major spring flooding in most Manitoba basins is low. Due to below normal soil moisture at freeze-up in southern and central Manitoba basins and below normal to well below normal winter precipitation until mid-February in these basins, the risk of major spring flooding is low for all southern and central Manitoba basins. Southern and central Manitoba basins include the Assiniboine River, Red River, Souris River, Pembina River, Roseau River and Qu’Appelle River basins and Interlake region. The risk of major spring flooding is low to moderate for northern Manitoba basins, including the Saskatchewan and Churchill River basins, because these basins have normal to above normal soil moisture and received below normal to slightly above normal winter precipitation. Most of the major lakes are below normal levels for this time of the year and within their operating ranges. The risk of flooding for most lakes is low. Soil Moisture Conditions at Freeze up: Soil moisture at freeze-up is one of the major factors that affects spring runoff potential and spring flood risk. Due to normal to below normal summer and fall precipitation, the soil moisture at freeze-up is normal to below normal for most of the southern and central Manitoba basins. Soil moisture is normal to above normal in the Little Saskatchewan River basin and in areas close to Brandon. -

Provincial Flood Control Infrastructure Review of Operating Guidelines
A REPORT TO THE MINISTER OF MANITOBA INFRASTRUCTURE AND TRANSPORTATION August 2015 2 - Provincial Flood Control Infrastructure Panel Members Harold Westdal Chair Rick Bowering Hydrological Engineer Barry MacBride Civil Engineer Review of Operating Guidelines - 3 ACKNOWLEDGEMENTS While much of the work in this report is technical in nature, that work can only be guided and have meaning within a human context. In this respect the Panel is deeply grateful to the large numbers of people who freely gave their time and provided the Panel with the benefit of their experience and knowledge. The Panel would like to acknowledge the work of David Faurschou and Marr Consulting, the participation of municipal governments, First Nations, producer associations, provincial staff, those people who provided excellent advice at the Panel’s roundtable sessions and the many members of the public who took the time to attend open house sessions. The Panel also thanks the staff of the department for providing access to historical documents and technical support, and for attending the open house sessions. 4 - Provincial Flood Control Infrastructure TABLE OF CONTENTS 1 Flood Control Infrastructure Matters . .9 2 Terms of Reference and Approach .....................................13 2.1 Review Process .................................................14 2.2 Public Engagement. 15 2.3 Presentation of this Report .........................................15 3 Manitoba’s Flood Control System ......................................17 3.1 Diking ..................................................19 3.2 Flood Control Works ..............................................19 3.3 Benefits of the System ............................................19 4 Operating Guidelines and Rules .......................................25 4.1 Operating Guidelines in Practice .....................................26 4.2 Operational Considerations . 27 5 The Red River Floodway .............................................28 5.1 Background ..................................................28 5.1.1 How the Floodway Works . -

Regulation of Water Levels on Lake Manitoba and Along the Fairford River, Pineimuta Lake, Lake St
Regulation of Water Levels on Lake Manitoba and along the Fairford River, Pineimuta Lake, Lake St. Martin and Dauphin River and Related Issues A Report to the Manitoba Minister of Conservation Volume 2: Main Report July 2003 The Lake Manitoba Regulation Review Advisory Committee Cover Photo: Looking west along the Fairford River from the Fairford River Water Control Structure. Lake Manitoba Regulation Review Advisory Committee, Main Report, July 2003 Table of Contents 1.0 Introduction ........................................................................................................................... 4 1.1 Background ...................................................................................................................... 4 1.2 Establishment of the Lake Manitoba Regulation Review Advisory Committee ............. 4 1.3 Terms of Reference .......................................................................................................... 5 1.4 Overview of Committee Activities .................................................................................. 5 2.0 Lake Manitoba Drainage Basin ........................................................................................... 8 2.1 General Description.......................................................................................................... 8 2.1.1 Lake Winnipegosis.................................................................................................. 10 2.1.2 Lake Manitoba ....................................................................................................... -

Optimal Operation of a Flood Control Systen a Thesis
The University of Manitoba Optimal Operation of a Flood Control Systen by John Nairn MacKenzie A Thesis Submitted to the Faculty of Graduate Studies in Partial Fulfilment of the Requirements for the Degree of It{aster of Science Tl¡-nr+man+ l'ir¡i'l DePdL Llllu.lIL ^.Ê\JI \,-LVI-L FnoinoarinoLtlSrIrçvf rrrð WitIrIulft/võ, nn i nco l\4en i toba Arrmrcf I q7R C)PTiIIAL OPEIIAÏIÛN OT A FLOOD CÛNTRC]L SYSÏËi4 BY JOHN I.IÄIRÎ''J I.4¡CKEI{Z] E A clissertation submiÈted to tåte Facr*lty of Cr*ci".¡aÉe Stuse.åies of' tlre University oá' Munitoba ire partLrl f'uifilln'le¡rt ol' t!re requle'ernemts ol'tlre clegrce ot IIAST TR OF S C I ENC E o,ig78 Fernrissio¡r hus bec¡r gnunted Ëo the t-l¡ì$l,AÊLV ûF Te!U U¡{l\¡¡-:F¿- S¡TV Ol.' h{.4þ]lTO!3"4 tr¡ lenei q¡r s¿:l! copies oü t!¡is cåÈ*;ertati{!r¡" 8o the N,4TltNAL [.N8¡4,ARY ûFr {lA"l\Ai}A to l¡riar¡:*'ilrsr tl¡ls ciissertafio¡r and tr: lend or sell copies of the felnr, und {,JNl'VUåì,5åTY h{lCfì,OFlLh{S tr: pubiish i¡¡r ahsåraet of this rJissert¿¡f ion. The ar¡thor re$erve$ otå:cr publ!c¿¡Èir¡¡r rights, ¿¡¡rJ ¡"¡either the dissertation ncr exÉensive cxtri¡cfs fr¡:nr it mluy h*: gx'int*d eir otl¡er- wise repi:oeíLlced evithout t !¡c uuf l¡o¡''s writËc¡r 3:cnrr ieslr.xr" ACI$IOWLEDffiIvE\TS I would like to e4press my appTeciation to my advisor, Professor G. -
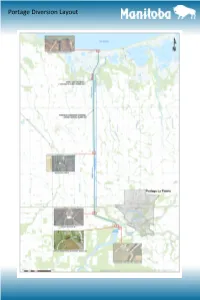
Portage Diversion Layout Recent and Future Projects
Portage Diversion Layout Recent and Future Projects Assiniboine River Control Structure Public and worker safety improvements Completed in 2015 Works include fencing, signage, and safety boom Electrical and mechanical upgrades Ongoing Works include upgrades to 600V electrical distribution system, replacement of gate control system and mo- tor control center, new bulkhead gate hoist, new stand-by diesel generator fuel/piping system and new ex- terior diesel generator Portage Diversion East Outside Drain Reconstruction of 18 km of drain Completed in 2013 Replacement of culverts beneath three (3) railway crossings Completed in 2018 Recent and Future Projects Portage Diversion Outlet Structure Construction of temporary rock apron to stabilize outlet structure Completed in 2018 Conceptual Design for options to repair or replace structure Completed in 2018 Outlet structure major repair or replacement prioritized over next few years Portage Diversion Channel Removal of sedimentation within channel Completed in 2017 Groundwater/soil salinity study for the Portage Diversion Ongoing—commenced in 2016 Enhancement of East Dike north of PR 227 to address freeboard is- sues at design capacity of 25,000 cfs Proposed to commence in 2018 Multi-phase over the next couple of years Failsafe assessment and potential enhancement of West Dike to han- dle design capacity of 25,000 cfs Prioritized for future years—yet to be approved Historical Operating Guidelines Portage Diversion Operating Guidelines 1984 Red River Floodway Program of Operation Operation Objectives The Portage Diversion will be operated to meet these objectives: 1. To provide maximum benefits to the City of Winnipeg and areas along the Assiniboine River downstream of Portage la Prairie. -

Multiculturalism in the Past
MULTICULTURALISM IN THE PAST Leo Pettipas Manitoba Archaeological Society Multicultural: Of or having a number [two or more] of distinct cultures existing side by side in the same country, province, etc. — Gage Canadian Dictionary. In Canada, multiculturalism is considered to be of sufficient value as to merit support and promotion by way of legislation, official policy, and public programming. In Manitoba, multicultural heritage is celebrated each year in the many ethnic festivals and celebrations held throughout the province. The most conspicuous acknowledgement of our past and present cultural diversity is Winnipeg's internationally renowned festival of the nations, Folklorama. As an everyday aspect of human experience, multiculturalism ("cultural plurality" is perhaps a better term) is nothing new. Numerous examples of it are to be found well back into Manitoba's Indigenous past. Traditional Cree teachings, for example, speak of the "Ancients" -- people of distinct cultural heritage who lived in the North before and at the time of the arrival of the Crees themselves, and with whom the Crees became acquainted when they took up residence there many generations ago. Archaeological discoveries dating to before European contact in southern Manitoba are also believed to reflect cultural diversity in this region in Pre-Contact times. During the 1980s, archaeologists working on the riverbank at Lockport found evidence of a community whose roots lay to the south in what is now the American Upper Midwest. Their pottery in particular reflects non-local origins, as does their economy: they were cultivators of domesticated plants, unlike their local neighbours whose diet was based on the consumption of wild faunal and floral food resources.