Nehari's Theorem for Convex Domain Hankel and Toeplitz Operators In
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Immigrants I Through K
I Iager, John, Switzerland, came to the county in 1865, in Newton County 1882 Atlas, patrons, from Missouri Pioneers Volume XVI Iberg, Jacob, Switzerland, 81, in the 1900 Federal Census of Newton CO, MO, Neosho Township Iburg, Herman C., Germany, 54, in the 1910 Federal Census of St. Clair CO, MO, Jackson Township. Also, Herman C. Iburg, Oenhousen [Oeynhausen ?], Germany, born February 23, 1855 [MO death certificate] died October 3, 1910, in St. Clair County, father John Iburg, mother Christina Daniels, informant Mrs. Herman C. Iburg Ihde, William, Petersdorf Cris Templen, Germany, from a 1915 petition for naturalization, McDonald County, Missouri, from Missouri Pioneers Volume XXVIII. Also, William Ihde, Germany, 59, in the 1920 Federal Census of McDonald CO, MO, Cyclone Ikenruth, Adam, Germany, 52, in the 1910 Federal Census of Cedar CO, MO, Linn Township Iker, Joseph, Baden, Germany, 37, in the 1870 Federal Census of Hickory CO, MO, Montgomery Township Iles, Thomas, England, 60, in the 1910 Federal Census of Dade CO, MO, Grant Township. [On son William Carl Iles’ MO death certificate from Dade County father is listed as Thomas Iles born in England and mother Ellen Perr__man[?] ] Imme, Adolph, Germany, 55, in the 1900 Federal Census of Jasper CO, MO, Webb City Immel, John, Germany, born January 28, 1834 [MO death certificate] died August 24, 1917, in Joplin, Jasper County. And, 68, in the 1900 Federal Census of Jasper CO, MO, Joplin Immel, Mrs. Katherine, Germany, born October 7, 1849 [MO death certificate] died June 1, 1933, in Joplin, Jasper County, father Christian Miller, mother Marie Hoffman, husband [deceased] John Immel Inch, Jack, England, 32, born May, 1868, in the 1900 Federal Census of Lawrence CO, MO, Vineyard Township Indermuehle, Gottlieb, Canton Bern, Switzerland, born March 14, 1830 [MO death certificate] died March 4, 1912, in Laclede County, father Christain Indermuehle, informant J. -

Leadership That Lifts Us All Recognizing Outstanding Philanthropy 2017 - 2018
Leadership That Lifts Us All Recognizing Outstanding Philanthropy 2017 - 2018 uwswpa.org Thank you to our 2017 sponsors: Premier Gold Dear Friends, As philanthropic leaders who, through their generous gifts of time and treasure, demonstrate their commitment to tackling our community’s most pressing problems, we should be proud of the impact we make on the lives of people who need our help. Through our gifts – Tocqueville Society members contributed nearly $10 million to the United Way 2017 Campaign – the most vulnerable members of our community are getting much-needed support: Dan Onorato • local children like Alijah (page 18) are matched with caring mentors who are helping them plan to continue their education after high school; • seniors like Jean (page 4) are receiving support that helps them remain in the homes they love; • people with disabilities like Kenny (page 9) are getting the opportunity to find 1 meaningful work; and • women like Sarah (page 43) are able to overcome challenges in order to gain greater financial stability. On behalf of our community, thank you for your support. Your gift helps United Way put solutions into action, making a difference and encouraging hope for a better David Schlosser tomorrow for everyone. With warmest regards Dan Onorato David Schlosser 2017 Tocqueville Society Co-Chair 2017 Tocqueville Society Co-Chair 2017 Top Tocqueville Corporations The Tocqueville Society Tocqueville Society Membership Growth United Way recognizes these United Way’s Tocqueville Society is corporations that had the largest comprised of philanthropic leaders 2011 430 number of Tocqueville Society and volunteer champions who donors for the 2017 campaign, give $10,000 or more annually to regardless of company size or United Way, creating a profound 2012 458 overall campaign total. -

Names of Scientists Associated with Discoveries of Elements of Periodic Table
Dr. John Andraos, http://www.careerchem.com/NAMED/Elements-Discoverers.pdf 1 NAMES OF SCIENTISTS ASSOCIATED WITH DISCOVERIES OF ELEMENTS OF PERIODIC TABLE © Dr. John Andraos 2002 - 2005 Department of Chemistry, York University 4700 Keele Street, Toronto, ONTARIO M3J 1P3, CANADA For suggestions, corrections, additional information, and comments please send e-mails to [email protected] http://www.chem.yorku.ca/NAMED/ Z, Element Symbol Discoverer Dates Nationality Place and Date of Discovery 1. Hydrogen H Cavendish, 1731 - 1810 British (b. Nice, France) 1766 Henry London, England 2. Helium He Janssen, Pierre 1824 - 1907 French 1868 Jules Cesar (b. Paris, France) Ramsay, Sir 1852 - 1916 Scottish 1895 William (b. Glasgow, Scotland) London, England 3. Lithium Li Arfvedson, 1792 - 1841 Swedish (b. Skagerholms- 1817/1818 Johann August Bruk, Skaraborgs-Län, Stockholm, Sweden Sweden) Dr. John Andraos, http://www.careerchem.com/NAMED/Elements-Discoverers.pdf 2 4. Beryllium Be Vauquelin, Louis 1763 - 1829 French (b. Saint-André 1797 Nicolas d'Héberôt, Calvados, Paris, France France) 5. Boron B Gay-Lussac, 1778 - 1850 French (b. St. 1808 Joseph Louis Léonard, Haute Paris, France Vienne, France) London, England Thénard, Louis 1777 - 1857 French (b. Louptière, Jacques France) Davy, Sir 1778 - 1829 British Humphry (b. Penzance, Cornwall, England) 6. Carbon C N/A N/A N/A pre-history 7. Nitrogen N Rutherford, 1749 - 1819 Scottish 1772 Daniel (b. Edinburgh, Scotland) Edinburgh, Scotland 8. Oxygen O Priestley, Joseph 1733 - 1804 British 1774 (b. Fieldhead, near Leeds, Leeds, England England) Scheele, Carl 1742 - 1786 Swedish Uppsala, Sweden Wilhelm (b. Stralsund, Pomerania, now in Germany) 9. Fluorine F Moissan, Henri 1852 - 1907 French (b. -
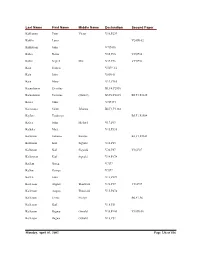
Delta County Naturalization Name Index
Last Name First Name Middle Name Declaration Second Paper Kahkonen Peter Victor V16,P239 Kahllo Louis V24,P102 Kahlstrom John V7,P436 Kahra Reino V35,P36 V35,P36 Kahra Segred Mrs. V35,P36 V35,P36 Kain Francis V5,P9 1/2 Kain John V8,P101 Kain Mary V19,P165 Kainulainen Eventius B1,F4,P2930 Kainulainen Eventius (Daniel) B5,F2,P2635 B5,F1,P2635 Kaiser John V7,P434 Kaivosoja Saimi Johanna B2,F1,P3144 Kajfasz Teodozya B5,F1,P2584 Kalies John Michael V17,P63 Kalkala Matt V15,P336 Kallarson Johanna Katrina B3,F1,P2101 Kallarson Karl Sigvald V18,P83 Kallarson Karl Sigwald V36,P87 V36,P87 Kallarsson Karl Sigvald V14,P178 Kallem Goreg V7,P7 Kallen George V7,P7 Kallen John V13,P329 Kallerson August Thorwald V31,P37 V31,P37 Kallerson August Thouvald V15,P474 Kallerson Jennie Evelyn B6,F1,P6 Kallerson Karl V18,P51 Kallerson Ragnar Oswald V35,P100 V35,P100 Kallerson Ragnar Oswald V18,P52 Monday, April 01, 2002 Page 236 of 536 Last Name First Name Middle Name Declaration Second Paper Kallersson Karl V38,P6 V38,P6 Kallin John V30,P78 V30,P78 Kallin Peter V26,P55 V26,P55 Kallin Peter V12,P480 Kallio Elma Wilhelmina B1,F4,P2987 Kallio Elma Wilhemiina B4,F4,P2509 B4,F4,P2509 Kallio Johan Victor B1,F3,P2876 Kallio Johan Vihtori B4,F4,P2448 B4,F4,P2448 Kallman And V12,P168 Kallman John V12,P167 Kallman John V7,P267 Kallman John V24,P110 Kallman John V20,P185 Kallman Lars E. V12,P79 Kallorssen Johanna B3,F1,P2101 Kalorssen Karl V38,P6 V38,P6 Kalsen Johannes V11,P171 Kamarainen Seth V15,P420 Kamarainen Seth V19,P92 Kamb Andre V8,P419 kAmerson Andrew V8,P426 Kaminen Oskar V31,P93 V31,P93 Kaminen Oskar V15,P167 Kamovich Mark V17,P284 Kampe Herman V5,P31 Kampe John E. -
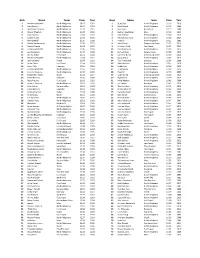
Girls Name Team Time Year Boys Name Team Time
Girls Name Team Time Year Boys Name Team Time Year 1 Marianne Abdalah North Allegheny 10:47 2012 1 Scott Seel North Allegheny 10:13 2010 2 Clara Savchik North Allegheny 11:07 2013 2 Mike Becich North Allegheny 10:15 2009 3 Madeleine Davison North Allegheny 11:19 2011 3 John Faye Hempfield 10:19 2008 4 Allyson Meehan North Allegheny 11:28 2013 4 Zachary Leachman Mars 10:19 2015 5 Clara Savchik North Allegheny 11:34 2012 5 Jack Bertram North Allegheny 10:20 2019 6 Sydney Kuder North Allegheny 11:34 2019 6 Michael Gauntner North Allegheny 10:22 2019 7 Alex Gambill North Allegheny 11:35 2008 7 Ryan Gil North Allegheny 10:25 2006 8 Rachel Hockenberry North Allegheny 11:38 2017 8 Mark Brown Greensburg Salem 10:25 2014 9 Maura Mlecko North Allegheny 11:44 2017 9 Christian Fitch Fox Chapel 10:27 2015 10 Lindsay Holdcroft North Allegheny 11:45 2005 10 Daniel McGoey North Allegheny 10:29 2015 11 Lexi Sundgren North Allegheny 11:48 2018 11 Samuel West Seneca Valley 10:29 2019 12 Annika Urban Fox Chapel 11:52 2014 12 Cameron Binda Greensburg Salem 10:30 2014 13 Marianne Abdalah North Allegheny 11:53 2011 13 Jacob Greco North Allegheny 10:32 2012 14 Jolene Kunkel Knoch 11:54 2006 14 Tyler Palenchak Gateway 10:34 2008 15 Laura Carter Fox Chapel 11:54 2019 15 Matt McGoey North Allegheny 10:35 2010 16 Kevyn Fish Hampton 11:54 2019 16 Bobby Lutz North Allegheny 10:38 2012 17 Lindsay Holdcroft North Allegheny 11:55 2004 17 TJ Robinson North Allegheny 10:39 2013 18 Caroline Cwalina North Allegheny 11:57 2009 18 Ryan Gil North Allegheny 10:40 2005 19 Samantha -

Variability of Multi-Omics Profiles in a Population-Based Child Cohort
Gallego-Paüls et al. BMC Medicine (2021) 19:166 https://doi.org/10.1186/s12916-021-02027-z RESEARCH ARTICLE Open Access Variability of multi-omics profiles in a population-based child cohort Marta Gallego-Paüls1,2,3, Carles Hernández-Ferrer1,2,3, Mariona Bustamante1,2,3,4, Xavier Basagaña1,2,3, Jose Barrera-Gómez1,2,3, Chung-Ho E. Lau5,6, Alexandros P. Siskos7, Marta Vives-Usano1,2,3,4, Carlos Ruiz-Arenas1,2,3, John Wright8, Remy Slama9, Barbara Heude10, Maribel Casas1,2,3, Regina Grazuleviciene11, Leda Chatzi12, Eva Borràs2,4, Eduard Sabidó2,4, Ángel Carracedo13,14, Xavier Estivill4, Jose Urquiza1,2,3, Muireann Coen6,15, Hector C. Keun7, Juan R. González1,2,3, Martine Vrijheid1,2,3 and Léa Maitre1,2,3* Abstract Background: Multiple omics technologies are increasingly applied to detect early, subtle molecular responses to environmental stressors for future disease risk prevention. However, there is an urgent need for further evaluation of stability and variability of omics profiles in healthy individuals, especially during childhood. Methods: We aimed to estimate intra-, inter-individual and cohort variability of multi-omics profiles (blood DNA methylation, gene expression, miRNA, proteins and serum and urine metabolites) measured 6 months apart in 156 healthy children from five European countries. We further performed a multi-omics network analysis to establish clusters of co-varying omics features and assessed the contribution of key variables (including biological traits and sample collection parameters) to omics variability. Results: All omics displayed a large range of intra- and inter-individual variability depending on each omics feature, although all presented a highest median intra-individual variability. -

(TRK) Fusion Cancer
Pathology & Oncology Research (2020) 26:1385–1399 https://doi.org/10.1007/s12253-019-00685-2 REVIEW Methods for Identifying Patients with Tropomyosin Receptor Kinase (TRK) Fusion Cancer Derek Wong1 & Stephen Yip1 & Poul H. Sorensen2,3,4 Received: 14 December 2018 /Accepted: 11 June 2019 /Published online: 29 June 2019 # Arányi Lajos Foundation 2019 Abstract NTRK gene fusions affecting the tropomyosin receptor kinase (TRK) protein family have been found to be oncogenic drivers in a broad range of cancers. Small molecule inhibitors targeting TRK activity, such as the recently Food and Drug Administration-approved agent larotrectinib (Vitrakvi®), have shown promising efficacy and safety data in the treatment of patients with TRK fusion cancers. NTRK gene fusions can be detected using several different ap- proaches, including fluorescent in situ hybridization, reverse transcription polymerase chain reaction, immunohisto- chemistry, next-generation sequencing, and ribonucleic acid-based multiplexed assays. Identifying patients with can- cers that harbor NTRK gene fusions will optimize treatment outcomes by providing targeted precision therapy. Keywords NTRK gene fusions . TRK fusions . TRK inhibitors . Next-generation sequencing . NGS Introduction the phosphoinositide 3-kinase/protein kinase B (PI3K-AKT) and mitogen-activated protein kinase (MAPK) signaling cas- TRK Receptor Family and Signaling cades [2–5](Fig.1). The tropomyosin receptor kinase (TRK) family is a NTRK Gene Fusions group of three neurotrophic receptor tyrosine kinase proteins (TRKA, TRKB, and TRKC) encoded by the Gene fusions involving the TRK protein family typically in- NTRK1, NTRK2, and NTRK3 genes located on chromo- volve intra- or inter-chromosomal rearrangements of the 5′ end somes 1q23.1, 9q21.33, and 15q25.3, respectively. -

List of Donors October 1 to Dec 31 2020
SOUTHERN OREGON FRIENDS OF HOSPICE DONORS – OCTOBER 1, 2020 – DECEMBER 31, 2020 $5000 and Above Sharon Kraatz Ross and Ronda Barker Acton Black Family Food Ron and Katharine Lang Esther Bell Program David Markewitz Benevity Angelina Black Joyce and Chris McKinney Becki Bernard Carrico Family Foundation Dr. Vera Melnyk and Dr. Paul Lynn Black Courtney M. Mullin Fund of the Jorizzo Sandra Black California Community Art and Thea Mills Janice Blodgett Foundation Dr. Mike and Trish Narus Don and Elizabeth Blue Martha Daura Sarah Nordquist Judith Blue J. Paul and Geertje De Vos Douglas Peterson Marcia Blum John and Marilyn Duke Diana Quirk Marydee Bombick Norman and Patty Fincher Bonnie and John Rinaldi Sharon Bradfield Bruce and Carolyn Johnson Marlene Rosen Barbara Bradley and John Burks Kathy and Dana Knoke Susan P. Rust Dr. John and Lorrie Brawner Lyn McConnell Colleen Searle Rob Bremer Jed and Celia Meese Sarah and Jack Seybold Judy and Bill Brodsky Merle and Peter Mullin Elaine Sharlach Kate Brophy Harry and Barbara Oliver Shirley South Chaz and Virginia Brown Donna Ritchie Randy and Bonnie Stroh Don Buckingham Allan and Dianne Rowell Judith and Steve Stromberg Janice Burr Dr. Baiba Rozkalns and Dr. J. David Strother Bryant Calhoun Lenna Burton Suzanne Taylor Dawn and Patrick Caldwell Donald and Elaine Turcke David and Elizabeth Candelaria $1000 and Above Dr. Charles and Becky Versteeg Eva and Linda Cannon Lori Williams and Thomas Jan Carlson Bill Adler Skinner Marion Carmichael The Autzen Foundation Jerrye Wright The Carmichael Group, LLC Carolyn and Jerry Barrett Elizabeth York William Carpenter and Pamela Janet L. -

Pittsburgh Legal Journal Friday, February 23, 2018
6 • Pittsburgh Legal Journal Friday, February 23, 2018 In the Commonwealth of Pennsylvania, Truskowski, Christian J. Truskowski, in His Forest Hills In the Commonwealth of Pennsylvania, County of Allegheny, Borough of Baldwin: Capacity as Devisee of the Estate of Dolores County of Allegheny, Borough of Heidelberg: LEGAL ADS Having erected thereon a one story brick Truskowski and John T. Truskowski, in His Having erected thereon an industrial heavy house being known as 5243 Becky Drive, Capacity as Devisee of the Estate of Dolores 48. RBI 2299, LLC manufacturing building being known as 500 Sheriff’s Sale Pittsburgh, PA 15236. Deed Book Volume Truskowski GD-17-000291—$7,080.64 Industry Way, Carnegie, PA 15106. Deed Book William P. Mullen, Sheriff 13417, Page 81. Block & Lot No. 390-E-240. MG-13-000564—$118,736.35 Joseph W. Gramc, Esq. Volume 11130, Page 234. Block & Lot No. 101- Abstracts of properties taken in Peter Wapner, Esq. 412-281-0587 B-365. execution upon the writs shown, at the 60. Anthony A. Antosz 215-563-7000 In the Commonwealth of Pennsylvania, numbers and terms shown, as the MG-17-001052—$94,991.96 In the Commonwealth of Pennsylvania, County of Allegheny, Borough of Forest Hills: Indiana properties of the severally named Shapiro & DeNardo, LLC County of Allegheny, Borough of Coraopolis: Having erected thereon a two story brick defendants, owners or reputed owners and 610-278-6800 Having erected thereon a dwelling being commercial building being known as 2205 to be sold by William P. Mullen, Sheriff of In the Commonwealth of Pennsylvania, known and numbered as 1217 Vance Avenue, Ardmore Boulevard, Pittsburgh, PA 15221. -

Basic Repertoire List
Basic Repertoire List for Building a Library of Classical Recordings How to Use this Guide The world of classical music spans nearly 10 centuries, and encompasses a multitude of styles, forms, and purposes. This section of the Guide was compiled in the hope that it will help and encourage many people in the exploration of the abundance of recorded classical music that is now available. With that in mind, this section focuses on those composers and compositions that provide a basic repertoire of music representing the various major styles and forms developed over the past millennium in Western Art Music. The Classical Net staff has assembled a list of compositions that we feel form a solid basis for a music collection that contains representative works from all periods and styles of the last millenium in Western art music. The compositions we have marked with an red star ( or asterisk *) are those we feel are fundamental and a good starting point for getting acquainted with more music by a particular composer or historic period. At the time this list was prepared every attempt was made to ensure that recordings of all the compositions listed are currently available. However, availability of recordings is at times a complex and fast-changing issue complicated by distributor and manufacturer offerings in various countries and even regions within countries, as well as changes in label ownership. This list has been designed to provide a roadmap to classical music in its many forms and styles, and to assist the user in acquiring a collection of recordings which bring this music into the home. -

Page 47 BERNARDS TOWNSHIP BOARD of EDUCATION BASKING RIDGE, NEW JERSEY MINUTES INDEX AUGUST 24, 2020 REGULAR SESSION 5:30 P.M. E
Page 47 BERNARDS TOWNSHIP BOARD OF EDUCATION BASKING RIDGE, NEW JERSEY MINUTES INDEX AUGUST 24, 2020 REGULAR SESSION 5:30 P.M. EXECUTIVE SESSION 5:37 P.M. REGULAR SESSION 7:02 P.M. VIRTUAL MEETING - INSTRUCTIONS TO PARTICIPATE IN THE VIRTUAL MEETING WILL BE POSTED BY 6:00PM ON AUGUST 24, 2020 AT WWW.BERNARDSBOE.COM I. Regular Session – Call to Order – 5:30 p.m. – page 51 II. Salute to the Flag – page 51 III. Roll Call – page 51 IV. Executive Session – 5:37 p.m. – page 51 V. Reconvene Regular Session – Call to Order – 7:02 p.m. – page 52 VI. Statement of Public Notice – page 52 VII. Board Presentation – page 53 1) The Return to Instruction Plan - Administrative Team VIII. Public Comment on Agenda Items – page 54 IX. Superintendent’s Report 1) Approve Submission The Return to Instruction Plan to Department of Education 2020-21 School Year – page 55 X. Approval of Minutes XI. Finance Committee Report 1) Approve List of Disbursements Dated August 24, 2020 – page 56 2) Acknowledge Receipt of June 2020 Financial Reports – page 56 3) Approve June 2020 Line Item Transfers – page 56 4) Approve Professional Development Expenses 2020-21 School Year – page 56 5) Approve Donation T-Mobile NY – page 57 6) Acknowledge Receipt Waste Disposal Bid & Award Contract – page Board of Education Minutes August 24, 2020 Page 48 57 7) Approve Contract Delaware Valley Regional High School Transportation – page 57 8) Approve Contract Barker Bus Company – page 58 9) Approve Stipulation of Settlement -

Surnames Beginning With
Card# Mine Name Operator Year Month Day Surname First and Middle Name Age Fata./Nonfatal In/Outside Occupation Nationality Citizen/Alien Single/Married #Children Mine Experience Occupation Exp. Accident Cause or Remarks Fault County Page# Mining Dist. Film# 48 Archbald Glen Alden Coal 1927 10 21 Kabeski Frank 20 nonfatal inside laborer Polish alien single fall coal topping off car gangway Lackawanna 414 5th 3589 52 Truesdale 1915 12 3 Kabillie Mike 63 fatal inside doorboy Lithuanian citizen married 4 killed by cars on gangway unavoidable 122 10th 6028 86 Jeddo No.4 Jeddo Highland Coal 1927 12 28 Kabley Foster 20 nonfatal outside laborer American citizen single rail piece broke off & struck him Luzerne 535 15th 3589 84 Loree Hudson Coal 1930 11 7 Kablonski Frank 20 nonfatal inside laborer Polish citizen single struck by falling collar pillar work Luzerne 105 12th 3590 14 Gravity Slope Hudson Coal 1927 4 8 Kacar John 20 nonfatal inside runner Polish single caught by derailed car spragging Lackawanna 376 2nd 3589 7 Loree No.5 Hudson Coal 1930 5 6 Kach Benjamin 33 fatal inside miner American citizen married 4 17 10 fall coal drilling hole in coal gangway accidental Luzerne 100 12th 3590 57 Dickson 1915 7 7 Kacha Michael 38 nonfatal inside laborer Lithuanian alien fall of roof unavoidable 90 2nd 6028 10 Stanton No.7 Lehigh WilkesBarre Coal 1928 2 13 Kachanski William 37 nonfatal inside miner Polish married caught between deraied car & gob Luzerne 123 11th 3589 42 Greenwood Lehigh Navigation Coal 1931 7 7 Kachilla Joseph 19 nonfatal outside