ARCHIMEDES What Did He Do Besides Cry Eureka?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Construction Surveying Curves
Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain. -

And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ. -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

From the Theorem of the Broken Chord to the Beginning of the Trigonometry
From the Theorem of the Broken Chord to the Beginning of the Trigonometry MARIA DRAKAKI Advisor Professor:Michael Lambrou Department of Mathematics and Applied Mathematics University of Crete May 2020 1/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 1 / 18 Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. -
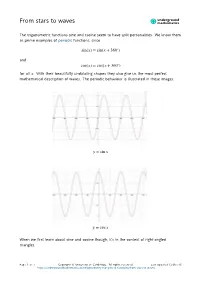
From Stars to Waves Mathematics
underground From stars to waves mathematics The trigonometric functions sine and cosine seem to have split personalities. We know them as prime examples of periodic functions, since sin(푥) = sin(푥 + 360∘) and cos(푥) = cos(푥 + 360∘) for all 푥. With their beautifully undulating shapes they also give us the most perfect mathematical description of waves. The periodic behaviour is illustrated in these images. 푦 = sin 푥 푦 = cos 푥 When we first learn about sine and cosine though, it’s in the context of right-angled triangles. Page 1 of 7 Copyright © University of Cambridge. All rights reserved. Last updated 12-Dec-16 https://undergroundmathematics.org/trigonometry-triangles-to-functions/from-stars-to-waves How do the two representations of these two functions fit together? Imagine looking up at the night sky and try to visualise the stars and planets all lying on a sphere that curves around us, with the Earth at its centre. This is called a celestial sphere. Around 2000 years ago, when early astronomers were trying to chart the night sky, doing astronomy meant doing geometry involving spheres—and that meant being able to do geometry involving circles. Looking at two stars on the celestial sphere, we can ask how far apart they are. We can formulate this as a problem about points on a circle. Given two points 퐴 and 퐵 on a cirle, what is the shortest distance between them, measured along the straight line that lies inside the circle? Such a straight line is called a chord of the circle. Page 2 of 7 Copyright © University of Cambridge. -

Lesson 2: Circles, Chords, Diameters, and Their Relationships
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M5 GEOMETRY Lesson 2: Circles, Chords, Diameters, and Their Relationships Student Outcomes . Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct the perpendicular bisector of a line segment and draw conclusions about points on that bisector and the endpoints of the segment. They relate the construction to the theorem stating that any perpendicular bisector of a chord must pass through the center of the circle. Classwork Opening Exercise (4 minutes) Scaffolding: Post a diagram and display the steps to create a Opening Exercise perpendicular bisector used in Construct the perpendicular bisector of line segment below (as you did in Module 1). Lesson 4 of Module 1. ���� Label the endpoints of the segment and . Draw circle with center and radius . Draw another line that bisects but is not perpendicular to it. Draw circle with center ���� and radius . List one similarity and one difference���� between the two bisectors. . Label the points of Answers will vary. All points on the perpendicular bisector are equidistant from points and 46T . ���� Points on the other bisector are not equidistant from points A and B. The perpendicular bisector intersection as and . meets at right angles. The other bisector meets at angles that are not congruent. Draw . ���� ⃖����⃗ You may wish to recall for students the definition of equidistant: EQUIDISTANT:. A point is said to be equidistant from two different points and if = . Points and can be replaced in the definition above with other figures (lines, etc.) as long as the distance to those figures is given meaning first. -

11.4 Arcs and Chords
Page 1 of 5 11.4 Arcs and Chords Goal By finding the perpendicular bisectors of two Use properties of chords of chords, an archaeologist can recreate a whole circles. plate from just one piece. This approach relies on Theorem 11.5, and is Key Words shown in Example 2. • congruent arcs p. 602 • perpendicular bisector p. 274 THEOREM 11.4 B Words If a diameter of a circle is perpendicular to a chord, then the diameter bisects the F chord and its arc. E G Symbols If BG&* ∏ FD&* , then DE&* c EF&* and DGs c GFs. D EXAMPLE 1 Find the Length of a Chord In ᭪C the diameter AF&* is perpendicular to BD&* . D Use the diagram to find the length of BD&* . 5 F C Solution E A Because AF&* is a diameter that is perpendicular to BD&* , you can use Theorem 11.4 to conclude that AF&* bisects B BD&* . So, BE ϭ ED ϭ 5. BD ϭ BE ϩ ED Segment Addition Postulate ϭ 5 ϩ 5 Substitute 5 for BE and ED . ϭ 10 Simplify. ANSWER ᮣ The length of BD&* is 10. Find the Length of a Segment 1. Find the length of JM&* . 2. Find the length of SR&* . H P 12 K C S C M N G 15 P J R 608 Chapter 11 Circles Page 2 of 5 THEOREM 11.5 Words If one chord is a perpendicular bisector M of another chord, then the first chord is a diameter. J P K Symbols If JK&* ∏ ML&* and MP&** c PL&* , then JK&* is a diameter. -

A Note on the History of Trigonometric Functions and Substitutions
A NOTE ON THE HISTORY OF TRIGONOMETRIC FUNCTIONS AND SUBSTITUTIONS Jean-Pierre Merlet INRIA, BP 93, 06902 Sophia-Antipolis Cedex France Abstract: Trigonometric functions appear very frequently in mechanism kinematic equations (for example as soon a revolute joint is involved in the mechanism). Dealing with these functions is difficult and trigonometric substi- tutions are used to transform them into algebraic terms that can be handled more easily. We present briefly the origin of the trigonometric functions and of these substitutions. Keywords: trigonometric substitutions, robotics 1 INTRODUCTION When dealing with the kinematic equations of a mechanism involving revolute joints appears frequently terms involving the sine and cosine of the revolute joint angles. Hence when solving either the direct or inverse kinematic equa- tions one has to deal with such terms. But the problem is that the geometric structure of the manifold build on such terms is not known and that only nu- merical method can be used to solve such equations. A classical approach to deal with this problem is to transform these terms into algebraic terms using the following substitution: θ 2t 1 − t2 t = tan( ) ⇒ sin(θ)= cos(θ)= 2 1+ t2 1+ t2 This substitution allows one to transform an equation involving the sine and cosine of an angle into an algebraic equation. Such type of equation has a structure that has been well studied in the past and for which a large number properties has been established, such as the topology of the resulting man- ifold and its geometrical properties. Furthermore efficient formal/numerical methods are available for solving systems of algebraic equations. -

Euclid Eworkshop # 6 Circle Geometry
Centre for Education in Mathematics and Computing Euclid eWorkshop # 6 Circle Geometry c 2014 UNIVERSITY OF WATERLOO Euclid eWorkshop #6 CIRCLE GEOMETRY CIRCLE GEOMETRY Geometry and more specifically the geometry of the circle represents an area of mathematics from which relatively difficult and interesting problems for the Euclid contest are frequently taken. Although this is a very broad content area, we present only a brief outline of some of the more elementary results of the geometry of the circle. We will assume that the student has some knowledge of the elementary properties of triangles, including congruence and sim- ilarity, as well as the properties of parallelograms, rhombi and trapezoids that follow from these properties of triangles. The ‘Star Trek’ Theorem The central angle subtended by any arc is twice any of the inscribed angles on that arc. In other words, in the accompanying figure \AOB = 2\ACB. Demonstration This theorem is the lynchpin of all the results that follow. It is useful to give a brief demonstration of this property to see that if follows directly from the properties of isosceles triangles. C O L A B In the diagram we draw the line connecting C and O and let a point on CO extended be L. Since OA, OB and OC are radii we have that the triangles OAC and OBC are isosceles. Thus \OAC = \OCA. Furthermore 1 OAC + OCA = AOL, the exterior angle of the triangle. Therefore OCA = ( AOL). Similarly \ \ \ \ 2 \ 1 OCB = ( BOL). \ 2 \ 1 1 Adding these 2 results ACB = ACO + OCB = ( AOL + LOB) = AOB. \ \ \ 2 \ \ 2\ Extensions See if you can extend this theorem to obtain each of the following: ◦ 1. -

Circle Geometry I Grade 11 CAPS Mathematics Series Outcome for This Topic
Circle Geometry I Grade 11 CAPS Mathematics Series Outcome for this Topic In this Topic we will : • Investigate and prove theorems linked to perpendicular bisectors of chords and solve related riders . Unit 1 • Investigate and prove theorems linked to inscribed and central angles and solve related riders . Unit 2 Unit 1 Theorems on Grade 11 Perpendicular CAPS Bisectors of Mathematics Series Chords Outcomes for Unit 1 In this Unit session we will : • Discuss the features of Geometric Axiomatic System. • Recap the terminology linked to circles. • Investigate and prove that : Segment from centre of circle perpendicular to chord bisects chord. (Theorem 1) • Investigate and prove that : Segment from centre of a circle to midpoint of chord is perpendicular to the chord. (Theorem 2) • Investigate and prove that : Perpendicular bisector of chord passes through the centre of a circle. (Theorem 3) • Solve riders related to Theorems 1, 2 and 3. Features of a Geometric Axiomatic System An Axiomatic System consists of some: Undefined terms Defined terms Axioms (Accepted unproved statements or proved theorems) Theorems (proved mathematical statements) Examples from Geometry : Undefined terms:Point, line (segment; ray), angle, triangle, exterior and interior angles of triangle Defined terms : A straight angle measures 180 Axiom 1: 12 corresponding angles are equal Axioms : Axiom 2: 12 alternate angles are equal Theorem 1: The sum of the interior angles of a triangle is equal to 180 Theorems : Theorem 2: The exterior angle of a triangle is equal -

3.2 Archimedes' Quadrature of the Parabola
3.2 Archimedes’ Quadrature of the Parabola 111 mere points for other functions to be defined on, a metalevel analysis with applications in quantum physics. At the close of the twentieth century, one of the hottest new fields in analysis is “wavelet theory,” emerging from such applications as edge de- tection or texture analysis in computer vision, data compression in signal analysis or image processing, turbulence, layering of underground earth sed- iments, and computer-aided design. Wavelets are an extension of Fourier’s idea of representing functions by superimposing waves given by sines or cosines. Since many oscillatory phenomena evolve in an unpredictable way over short intervals of time or space, the phenomenon is often better repre- sented by superimposing waves of only short duration, christened wavelets. This tight interplay between current applications and a new field of math- ematics is evolving so quickly that it is hard to see where it will lead even in the very near future [92]. We will conclude this chapter with an extraordinary modern twist to our long story. Recall that the infinitesimals of Leibniz, which had never been properly defined and were denigrated as fictional, had finally been banished from analysis by the successors of Cauchy in the nineteenth century, using a rigorous foundation for the real numbers. How surprising, then, that in 1960 deep methods of modern mathematical logic revived infinitesimals and gave them a new stature and role. In our final section we will read a few passages from the book Non-Standard Analysis [140] by Abraham Robinson (1918– 1974), who discovered how to place infinitesimals on a firm foundation, and we will consider the possible consequences of his discovery for the future as well as for our evaluation of the past. -

The Angle Trisection Solution (A Compass-Straightedge (Ruler) Construction) Kimuya .M
I S S N 2 3 4 7 - 1921 Volume 13 Number 4 Journal of Advance in Mathematics The Angle Trisection Solution (A Compass-Straightedge (Ruler) Construction) Kimuya .M. Alex1, Josephine Mutembei2 1Meru University of Science and Technology, Kenya, Department of Physical Sciences, Faculty of Physics 2Meru University of Science and Technology, Kenya, Department of Mathematics 1Cell; +254 704600418 2Cell; +254 721567967 [email protected] [email protected] ABSTRACT This paper is devoted to exposition of a provable classical solution for the ancient Greek’s classical geometric problem of angle trisection [3]. (Pierre Laurent Wantzel, 1837), presented an algebraic proof based on ideas from Galois theory showing that, the angle trisection solution correspond to an implicit solution of the cubic equation; , which he stated as geometrically irreducible [23]. The primary objective of this novel work is to show the possibility to solve the ages old problem of trisecting an arbitrary angle using the traditional Greek’s tools of geometry (classical compass and straightedge), and refute the presented proof of angle trisection impossibility statement. The exposed proof of the solution is theorem , which is based on the classical rules of Euclidean geometry, contrary to the Archim edes proposition of using a marked straightedge construction [4], [11]. Key Words Angle trisection; An arbitrary angle; A particular angle; Compass; Ruler (Straightedge); Classical geometry; GeoGebra Software; Plane geometry; Subset; Superset; Singular angle Notations Notation for an angle Denotes a straight line segment and a length Two Dimensions Three Dimensions Four significant figures Denotes a member or an element of a particular set Subset Not a member or an element of a particular set divides Cosine of angle decimal places Academic Discipline And Sub-Disciplines Mathematics (Geometry) 1.0 INTRODUCTION Compass and straightedge problems have always been the favorite subject o f classical geometry.