The Problem of Apollonius As an Opportunity for Teaching Students to Use Reflections and Rotations to Solve Geometry Problems Via Ga
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected]
Ursinus College Digital Commons @ Ursinus College Transforming Instruction in Undergraduate Pre-calculus and Trigonometry Mathematics via Primary Historical Sources (TRIUMPHS) Spring 3-2017 A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected] Follow this and additional works at: https://digitalcommons.ursinus.edu/triumphs_precalc Part of the Curriculum and Instruction Commons, Educational Methods Commons, Higher Education Commons, and the Science and Mathematics Education Commons Click here to let us know how access to this document benefits oy u. Recommended Citation Otero, Danny, "A Genetic Context for Understanding the Trigonometric Functions" (2017). Pre-calculus and Trigonometry. 1. https://digitalcommons.ursinus.edu/triumphs_precalc/1 This Course Materials is brought to you for free and open access by the Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) at Digital Commons @ Ursinus College. It has been accepted for inclusion in Pre-calculus and Trigonometry by an authorized administrator of Digital Commons @ Ursinus College. For more information, please contact [email protected]. A Genetic Context for Understanding the Trigonometric Functions Daniel E. Otero∗ July 22, 2019 Trigonometry is concerned with the measurements of angles about a central point (or of arcs of circles centered at that point) and quantities, geometrical and otherwise, that depend on the sizes of such angles (or the lengths of the corresponding arcs). It is one of those subjects that has become a standard part of the toolbox of every scientist and applied mathematician. It is the goal of this project to impart to students some of the story of where and how its central ideas first emerged, in an attempt to provide context for a modern study of this mathematical theory. -

Geometric Exercises in Paper Folding
MATH/STAT. T. SUNDARA ROW S Geometric Exercises in Paper Folding Edited and Revised by WOOSTER WOODRUFF BEMAN PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF MICHIGAK and DAVID EUGENE SMITH PROFESSOR OF MATHEMATICS IN TEACHERS 1 COLLEGE OF COLUMBIA UNIVERSITY WITH 87 ILLUSTRATIONS THIRD EDITION CHICAGO ::: LONDON THE OPEN COURT PUBLISHING COMPANY 1917 & XC? 4255 COPYRIGHT BY THE OPEN COURT PUBLISHING Co, 1901 PRINTED IN THE UNITED STATES OF AMERICA hn HATH EDITORS PREFACE. OUR attention was first attracted to Sundara Row s Geomet rical Exercises in Paper Folding by a reference in Klein s Vor- lesungen iiber ausgezucihlte Fragen der Elementargeometrie. An examination of the book, obtained after many vexatious delays, convinced us of its undoubted merits and of its probable value to American teachers and students of geometry. Accordingly we sought permission of the author to bring out an edition in this country, wnich permission was most generously granted. The purpose of the book is so fully set forth in the author s introduction that we need only to say that it is sure to prove of interest to every wide-awake teacher of geometry from the graded school to the college. The methods are so novel and the results so easily reached that they cannot fail to awaken enthusiasm. Our work as editors in this revision has been confined to some slight modifications of the proofs, some additions in the way of references, and the insertion of a considerable number of half-tone reproductions of actual photographs instead of the line-drawings of the original. W. W. -

Construction Surveying Curves
Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain. -

And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ. -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

Chapter 12, Lesson 1
i8o Chapter 12, Lesson 1 Chapter 12, Lesson 1 •14. They are perpendicular. 15. The longest chord is always a diameter; so Set I (pages 486-487) its length doesn't depend on the location of According to Matthys Levy and Mario Salvador! the point. The length of the shortest chord in their book titled \Nhy Buildings Fall Down depends on how far away from the center (Norton, 1992), the Romans built semicircular the point is; the greater the distance, the arches of the type illustrated in exercises 1 through shorter the chord. 5 that spanned as much as 100 feet. These arches Theorem 56. were used in the bridges of 50,000 miles of roads that the Romans built all the way from Baghdad 16. Perpendicular lines form right angles. to London! • 17. Two points determine a line. The conclusions of exercises 13 through 15 are supported by the fact that a diameter of a circle is •18. All radii of a circle are equal. its longest chord and by symmetry considerations. 19. Reflexive. As the second chord rotates away from the diameter in either direction about the point of 20. HL. intersection, it becomes progressively shorter. 21. Corresponding parts of congruent triangles are equal. Roman Arch. •22. If a line divides a line segment into two 1. Radii. equal parts, it bisects the segment. •2. Chords. Theorem 57. •3. A diameter. 23. If a line bisects a line segment, it divides the 4. Isosceles. Each has two equal sides because segment into two equal parts. the radii of a circle are equal. -

From the Theorem of the Broken Chord to the Beginning of the Trigonometry
From the Theorem of the Broken Chord to the Beginning of the Trigonometry MARIA DRAKAKI Advisor Professor:Michael Lambrou Department of Mathematics and Applied Mathematics University of Crete May 2020 1/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 1 / 18 Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. -
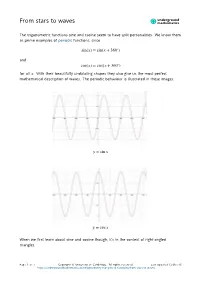
From Stars to Waves Mathematics
underground From stars to waves mathematics The trigonometric functions sine and cosine seem to have split personalities. We know them as prime examples of periodic functions, since sin(푥) = sin(푥 + 360∘) and cos(푥) = cos(푥 + 360∘) for all 푥. With their beautifully undulating shapes they also give us the most perfect mathematical description of waves. The periodic behaviour is illustrated in these images. 푦 = sin 푥 푦 = cos 푥 When we first learn about sine and cosine though, it’s in the context of right-angled triangles. Page 1 of 7 Copyright © University of Cambridge. All rights reserved. Last updated 12-Dec-16 https://undergroundmathematics.org/trigonometry-triangles-to-functions/from-stars-to-waves How do the two representations of these two functions fit together? Imagine looking up at the night sky and try to visualise the stars and planets all lying on a sphere that curves around us, with the Earth at its centre. This is called a celestial sphere. Around 2000 years ago, when early astronomers were trying to chart the night sky, doing astronomy meant doing geometry involving spheres—and that meant being able to do geometry involving circles. Looking at two stars on the celestial sphere, we can ask how far apart they are. We can formulate this as a problem about points on a circle. Given two points 퐴 and 퐵 on a cirle, what is the shortest distance between them, measured along the straight line that lies inside the circle? Such a straight line is called a chord of the circle. Page 2 of 7 Copyright © University of Cambridge. -

Constructibility
Appendix A Constructibility This book is dedicated to the synthetic (or axiomatic) approach to geometry, di- rectly inspired and motivated by the work of Greek geometers of antiquity. The Greek geometers achieved great work in geometry; but as we have seen, a few prob- lems resisted all their attempts (and all later attempts) at solution: circle squaring, trisecting the angle, duplicating the cube, constructing all regular polygons, to cite only the most popular ones. We conclude this book by proving why these various problems are insolvable via ruler and compass constructions. However, these proofs concerning ruler and compass constructions completely escape the scope of syn- thetic geometry which motivated them: the methods involved are highly algebraic and use theories such as that of fields and polynomials. This is why we these results are presented as appendices. Moreover, we shall freely use (with precise references) various algebraic results developed in [5], Trilogy II. We first review the theory of the minimal polynomial of an algebraic element in a field extension. Furthermore, since it will be essential for the applications, we prove the Eisenstein criterion for the irreducibility of (such) a (minimal) polynomial over the field of rational numbers. We then show how to associate a field with a given geometric configuration and we prove a formal criterion telling us—in terms of the associated fields—when one can pass from a given geometrical configuration to a more involved one, using only ruler and compass constructions. A.1 The Minimal Polynomial This section requires some familiarity with the theory of polynomials in one variable over a field K. -

Lesson 2: Circles, Chords, Diameters, and Their Relationships
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M5 GEOMETRY Lesson 2: Circles, Chords, Diameters, and Their Relationships Student Outcomes . Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct the perpendicular bisector of a line segment and draw conclusions about points on that bisector and the endpoints of the segment. They relate the construction to the theorem stating that any perpendicular bisector of a chord must pass through the center of the circle. Classwork Opening Exercise (4 minutes) Scaffolding: Post a diagram and display the steps to create a Opening Exercise perpendicular bisector used in Construct the perpendicular bisector of line segment below (as you did in Module 1). Lesson 4 of Module 1. ���� Label the endpoints of the segment and . Draw circle with center and radius . Draw another line that bisects but is not perpendicular to it. Draw circle with center ���� and radius . List one similarity and one difference���� between the two bisectors. . Label the points of Answers will vary. All points on the perpendicular bisector are equidistant from points and 46T . ���� Points on the other bisector are not equidistant from points A and B. The perpendicular bisector intersection as and . meets at right angles. The other bisector meets at angles that are not congruent. Draw . ���� ⃖����⃗ You may wish to recall for students the definition of equidistant: EQUIDISTANT:. A point is said to be equidistant from two different points and if = . Points and can be replaced in the definition above with other figures (lines, etc.) as long as the distance to those figures is given meaning first. -

11.4 Arcs and Chords
Page 1 of 5 11.4 Arcs and Chords Goal By finding the perpendicular bisectors of two Use properties of chords of chords, an archaeologist can recreate a whole circles. plate from just one piece. This approach relies on Theorem 11.5, and is Key Words shown in Example 2. • congruent arcs p. 602 • perpendicular bisector p. 274 THEOREM 11.4 B Words If a diameter of a circle is perpendicular to a chord, then the diameter bisects the F chord and its arc. E G Symbols If BG&* ∏ FD&* , then DE&* c EF&* and DGs c GFs. D EXAMPLE 1 Find the Length of a Chord In ᭪C the diameter AF&* is perpendicular to BD&* . D Use the diagram to find the length of BD&* . 5 F C Solution E A Because AF&* is a diameter that is perpendicular to BD&* , you can use Theorem 11.4 to conclude that AF&* bisects B BD&* . So, BE ϭ ED ϭ 5. BD ϭ BE ϩ ED Segment Addition Postulate ϭ 5 ϩ 5 Substitute 5 for BE and ED . ϭ 10 Simplify. ANSWER ᮣ The length of BD&* is 10. Find the Length of a Segment 1. Find the length of JM&* . 2. Find the length of SR&* . H P 12 K C S C M N G 15 P J R 608 Chapter 11 Circles Page 2 of 5 THEOREM 11.5 Words If one chord is a perpendicular bisector M of another chord, then the first chord is a diameter. J P K Symbols If JK&* ∏ ML&* and MP&** c PL&* , then JK&* is a diameter. -

Geometry, the Common Core, and Proof
Geometry, the Common Core, and Proof John T. Baldwin, Andreas Mueller Geometry, the Common Core, and Proof Overview From Geometry to Numbers John T. Baldwin, Andreas Mueller Proving the field axioms Interlude on Circles December 14, 2012 An Area function Side-splitter Pythagorean Theorem Irrational Numbers Outline Geometry, the Common Core, and Proof 1 Overview John T. Baldwin, 2 From Geometry to Numbers Andreas Mueller 3 Proving the field axioms Overview From Geometry to 4 Interlude on Circles Numbers Proving the 5 An Area function field axioms Interlude on Circles 6 Side-splitter An Area function 7 Pythagorean Theorem Side-splitter Pythagorean 8 Irrational Numbers Theorem Irrational Numbers Agenda Geometry, the Common Core, and Proof John T. Baldwin, Andreas 1 G-SRT4 { Context. Proving theorems about similarity Mueller 2 Proving that there is a field Overview 3 Areas of parallelograms and triangles From Geometry to Numbers 4 lunch/Discussion: Is it rational to fixate on the irrational? Proving the 5 Pythagoras, similarity and area field axioms Interlude on 6 reprise irrational numbers and Golden ratio Circles 7 resolving the worries about irrationals An Area function Side-splitter Pythagorean Theorem Irrational Numbers Logistics Geometry, the Common Core, and Proof John T. Baldwin, Andreas Mueller Overview From Geometry to Numbers Proving the field axioms Interlude on Circles An Area function Side-splitter Pythagorean Theorem Irrational Numbers Common Core Geometry, the Common Core, and Proof John T. Baldwin, G-SRT: Prove theorems involving similarity Andreas Mueller 4. Prove theorems about triangles. Theorems include: a line Overview parallel to one side of a triangle divides the other two From proportionally, and conversely; the Pythagorean Theorem Geometry to Numbers proved using triangle similarity.