DOCSLIB.ORG

11.4 Arcs and Chords

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
11.4 Arcs and Chords Page 1 of 5 11.4 Arcs and Chords Goal By finding the perpendicular bisectors of two Use properties of chords of chords, an archaeologist can recreate a whole circles. plate from just one piece. This approach relies on Theorem 11.5, and is Key Words shown in Example 2. • congruent arcs p. 602 • perpendicular bisector p. 274 THEOREM 11.4 B Words If a diameter of a circle is perpendicular to a chord, then the diameter bisects the F chord and its arc. E G Symbols If BG&* ∏ FD&* , then DE&* c EF&* and DGs c GFs. D EXAMPLE 1 Find the Length of a Chord In ᭪C the diameter AF&* is perpendicular to BD&* . D Use the diagram to find the length of BD&* . 5 F C Solution E A Because AF&* is a diameter that is perpendicular to BD&* , you can use Theorem 11.4 to conclude that AF&* bisects B BD&* . So, BE ϭ ED ϭ 5. BD ϭ BE ϩ ED Segment Addition Postulate ϭ 5 ϩ 5 Substitute 5 for BE and ED . ϭ 10 Simplify. ANSWER ᮣ The length of BD&* is 10. Find the Length of a Segment 1. Find the length of JM&* . 2. Find the length of SR&* . H P 12 K C S C M N G 15 P J R 608 Chapter 11 Circles Page 2 of 5 THEOREM 11.5 Words If one chord is a perpendicular bisector M of another chord, then the first chord is a diameter. J P K Symbols If JK&* ∏ ML&* and MP&** c PL&* , then JK&* is a diameter. L All diameters of a circle include the center of the circle. Therefore, the point where two diameters intersect is the center of the circle. Careers EXAMPLE 2 Find the Center of a Circle Suppose an archaeologist finds part of a circular plate. Show how to reconstruct the original shape of the plate. Solution ●1 Draw any two chords that are not parallel to each other. study ARCHAEOLOGISTS ●2 Draw the perpendicular bisector of and reconstruct artifacts each chord. These lines contain which provide information about past cultures. diameters. Career Links CLASSZONE.COM ●3 The diameters intersect at the circle’s center. Use a compass to draw the rest of the plate. THEOREM 11.6 Words In the same circle, or in congruent circles: • If two chords are congruent, then their corresponding minor arcs are congruent. A Student Help B • If two minor arcs are congruent, then their STUDY TIP D corresponding chords are congruent. If two central angles C are congruent then Symbols If AB&* c DC&* , then ABs c DCs. their corresponding arcs are congruent. If ABs c DCs, then AB&* c DC&* . 11.4 Arcs and Chords 609 Page 3 of 5 EXAMPLE 3 Find Measures of Angles and Chords Find the value of x. a. S b. 70 ؇ A B P R x ؇ 60 x؇ C C P 3 E D 70 ؇ Solution a. Because QP&* c RS&* , it follows that QPs c RSr. So, mQPs ϭ mRSr ϭ 60 Њ, and x ϭ 60. b. Because ABr c DEs, it follows that AB&* c DE&* . So, x ϭ DE ϭ 3. Find Measures of Angles and Chords Find the value of x. 3. 4.H 5. U V x ؉ 2 40 ؇ A E C W J G x 4 5 Y B D Z F (x ؉ 10) ؇ 11.411.4 Exercises Guided Practice Vocabulary Check 1. Identify a diameter. 2. Identify a pair of congruent arcs. C P B P A F C G D E S R Skill Check Find the value of x. 3.R 4.M 5. A x ؉ ؇ ( 5) D S 6 H N 8 T C B x C x ؊ 1 ؇ P P 50 E J K 610 Chapter 11 Circles Page 4 of 5 Practice and Applications Extra Practice Identifying Diameters Determine whether AB&* is a diameter of the See p. 695. circle. Explain your reasoning. 6. 7.A 8. C C A C E D 4 E 5 6 E A B ؇ 85 B 4 D B D Finding Chords and Central Angles Find the value of x. 9.A 10.A 11. A D x ؉ 7 B x C 35 ؇ 7 C C B D (x ؉ 6) ؇ B E E D 3x ؉ 1 Logical Reasoning Name any congruent arcs, chords, or angles. State a postulate or theorem that justifies your answer. 12.B 13.A 14. A ؇ C 90 B P P P C B D A C 90 ؇ D Finding Measures Find the measure of the red segment or arc. 15.B 16. 17. B B ؇ ؇ A E 110 D A 40 A C D 10 F E C E C ؇ 60 D Using Algebra Find the value of x. 18. 19. 20. B (2 x ؊ 10) ؇ A A A (x ؉ 45) ؇ x ؉ 6 C C C D E B D Homework Help 3x ؊ 8 4x؇ E (x ؉ 30) ؇ Example 1: Exs. 6–8, B D E 15–20 Example 2: Exs. 21–22 21. Example 3: Exs. 9–20 Visualize It! Draw a large circle and cut it out. Tear part of it off and ask another student to recreate your circle. 11.4 Arcs and Chords 611 Page 5 of 5 22. Avalanche Rescue Beacon An avalanche rescue beacon is a device used by backcountry skiers. It gives off a signal that is Careers detectable within a circle of a certain radius. In a practice drill, a ski patrol uses the following steps to locate a beacon buried in the snow. Explain how it works. 1 Walk in a straight line until the signal 2 Walk back to the halfway point, disappears. Turn around and walk and walk away from the line at a 90 Њ back until the signal disappears again. angle until the signal disappears. starting point EMTS Some Emergency Medical Technicians (EMTs) 3 Turn around and walk in a straight line 4 Walk back to the halfway point. train specifically for wilderness until the signal disappears again. You will be near the center of the emergencies. circle. The beacon is under you. Career Links CLASSZONE.COM hidden beacon Standardized Test 23. Multi-Step Problem Use the diagram below. ؇ Practice a. Explain why ADs c BEs. A 40 E b. x (15 x ؊ 40) ؇ (10 x ؉ 10) ؇ Find the value of . 5 5 c. Find mADs and mBEs. C D B d. Find mBDs. Mixed Review Measuring Arcs In the diagram below, AD&* and BE&* are diameters of ᭪F. Find the measure. (Lesson 11.3) E 24. mDEs 25. mBCs F A D mAEs 27. mBCDt 40 ؇ 65 ؇ .26 B 28. mABCs 29. mADEs C Algebra Skills Comparing Numbers Compare the two numbers. Write the answer (Skills Review, p. 662) .؍ using <, >, or 15 3 1 30. Ϫ26 and Ϫ29 31. ᎏᎏ and Ϫᎏᎏ 32. 0.2 and ᎏᎏ 20 4 5 612 Chapter 11 Circles.
Load more

Recommended publications
  • Proofs with Perpendicular Lines
    3.4 Proofs with Perpendicular Lines EEssentialssential QQuestionuestion What conjectures can you make about perpendicular lines? Writing Conjectures Work with a partner. Fold a piece of paper D in half twice. Label points on the two creases, as shown. a. Write a conjecture about AB— and CD — . Justify your conjecture. b. Write a conjecture about AO— and OB — . AOB Justify your conjecture. C Exploring a Segment Bisector Work with a partner. Fold and crease a piece A of paper, as shown. Label the ends of the crease as A and B. a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold. b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles? B Writing a Conjecture CONSTRUCTING Work with a partner. VIABLE a. Draw AB — , as shown. A ARGUMENTS b. Draw an arc with center A on each To be prof cient in math, side of AB — . Using the same compass you need to make setting, draw an arc with center B conjectures and build a on each side of AB— . Label the C O D logical progression of intersections of the arcs C and D. statements to explore the c. Draw CD — . Label its intersection truth of your conjectures. — with AB as O. Write a conjecture B about the resulting diagram. Justify your conjecture. CCommunicateommunicate YourYour AnswerAnswer 4. What conjectures can you make about perpendicular lines? 5. In Exploration 3, f nd AO and OB when AB = 4 units.
    [Show full text]
  • Construction Surveying Curves
    Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain.
    [Show full text]
  • And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
    9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ.
    [Show full text]
  • Chapter 1 – Symmetry of Molecules – P. 1
    Chapter 1 – Symmetry of Molecules – p. 1 - 1. Symmetry of Molecules 1.1 Symmetry Elements · Symmetry operation: Operation that transforms a molecule to an equivalent position and orientation, i.e. after the operation every point of the molecule is coincident with an equivalent point. · Symmetry element: Geometrical entity (line, plane or point) which respect to which one or more symmetry operations can be carried out. In molecules there are only four types of symmetry elements or operations: · Mirror planes: reflection with respect to plane; notation: s · Center of inversion: inversion of all atom positions with respect to inversion center, notation i · Proper axis: Rotation by 2p/n with respect to the axis, notation Cn · Improper axis: Rotation by 2p/n with respect to the axis, followed by reflection with respect to plane, perpendicular to axis, notation Sn Formally, this classification can be further simplified by expressing the inversion i as an improper rotation S2 and the reflection s as an improper rotation S1. Thus, the only symmetry elements in molecules are Cn and Sn. Important: Successive execution of two symmetry operation corresponds to another symmetry operation of the molecule. In order to make this statement a general rule, we require one more symmetry operation, the identity E. (1.1: Symmetry elements in CH4, successive execution of symmetry operations) 1.2. Systematic classification by symmetry groups According to their inherent symmetry elements, molecules can be classified systematically in so called symmetry groups. We use the so-called Schönfliess notation to name the groups, Chapter 1 – Symmetry of Molecules – p. 2 - which is the usual notation for molecules.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
  • From the Theorem of the Broken Chord to the Beginning of the Trigonometry
    From the Theorem of the Broken Chord to the Beginning of the Trigonometry MARIA DRAKAKI Advisor Professor:Michael Lambrou Department of Mathematics and Applied Mathematics University of Crete May 2020 1/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 1 / 18 Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction.
    [Show full text]
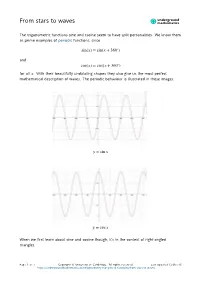
  • From Stars to Waves Mathematics
    underground From stars to waves mathematics The trigonometric functions sine and cosine seem to have split personalities. We know them as prime examples of periodic functions, since sin(푥) = sin(푥 + 360∘) and cos(푥) = cos(푥 + 360∘) for all 푥. With their beautifully undulating shapes they also give us the most perfect mathematical description of waves. The periodic behaviour is illustrated in these images. 푦 = sin 푥 푦 = cos 푥 When we first learn about sine and cosine though, it’s in the context of right-angled triangles. Page 1 of 7 Copyright © University of Cambridge. All rights reserved. Last updated 12-Dec-16 https://undergroundmathematics.org/trigonometry-triangles-to-functions/from-stars-to-waves How do the two representations of these two functions fit together? Imagine looking up at the night sky and try to visualise the stars and planets all lying on a sphere that curves around us, with the Earth at its centre. This is called a celestial sphere. Around 2000 years ago, when early astronomers were trying to chart the night sky, doing astronomy meant doing geometry involving spheres—and that meant being able to do geometry involving circles. Looking at two stars on the celestial sphere, we can ask how far apart they are. We can formulate this as a problem about points on a circle. Given two points 퐴 and 퐵 on a cirle, what is the shortest distance between them, measured along the straight line that lies inside the circle? Such a straight line is called a chord of the circle. Page 2 of 7 Copyright © University of Cambridge.
    [Show full text]
  • Symmetry in Chemistry - Group Theory
    Symmetry in Chemistry - Group Theory Group Theory is one of the most powerful mathematical tools used in Quantum Chemistry and Spectroscopy. It allows the user to predict, interpret, rationalize, and often simplify complex theory and data. At its heart is the fact that the Set of Operations associated with the Symmetry Elements of a molecule constitute a mathematical set called a Group. This allows the application of the mathematical theorems associated with such groups to the Symmetry Operations. All Symmetry Operations associated with isolated molecules can be characterized as Rotations: k (a) Proper Rotations: Cn ; k = 1,......, n k When k = n, Cn = E, the Identity Operation n indicates a rotation of 360/n where n = 1,.... k (b) Improper Rotations: Sn , k = 1,....., n k When k = 1, n = 1 Sn = , Reflection Operation k When k = 1, n = 2 Sn = i , Inversion Operation In general practice we distinguish Five types of operation: (i) E, Identity Operation k (ii) Cn , Proper Rotation about an axis (iii) , Reflection through a plane (iv) i, Inversion through a center k (v) Sn , Rotation about an an axis followed by reflection through a plane perpendicular to that axis. Each of these Symmetry Operations is associated with a Symmetry Element which is a point, a line, or a plane about which the operation is performed such that the molecule's orientation and position before and after the operation are indistinguishable. The Symmetry Elements associated with a molecule are: (i) A Proper Axis of Rotation: Cn where n = 1,.... This implies n-fold rotational symmetry about the axis.
    [Show full text]
  • CHAPTER 3 Parallel and Perpendicular Lines Chapter Outline
    www.ck12.org CHAPTER 3 Parallel and Perpendicular Lines Chapter Outline 3.1 LINES AND ANGLES 3.2 PROPERTIES OF PARALLEL LINES 3.3 PROVING LINES PARALLEL 3.4 PROPERTIES OF PERPENDICULAR LINES 3.5 PARALLEL AND PERPENDICULAR LINES IN THE COORDINATE PLANE 3.6 THE DISTANCE FORMULA 3.7 CHAPTER 3REVIEW In this chapter, you will explore the different relationships formed by parallel and perpendicular lines and planes. Different angle relationships will also be explored and what happens to these angles when lines are parallel. You will continue to use proofs, to prove that lines are parallel or perpendicular. There will also be a review of equations of lines and slopes and how we show algebraically that lines are parallel and perpendicular. 114 www.ck12.org Chapter 3. Parallel and Perpendicular Lines 3.1 Lines and Angles Learning Objectives • Identify parallel lines, skew lines, and parallel planes. • Use the Parallel Line Postulate and the Perpendicular Line Postulate. • Identify angles made by transversals. Review Queue 1. What is the equation of a line with slope -2 and passes through the point (0, 3)? 2. What is the equation of the line that passes through (3, 2) and (5, -6). 3. Change 4x − 3y = 12 into slope-intercept form. = 1 = − 4. Are y 3 x and y 3x perpendicular? How do you know? Know What? A partial map of Washington DC is shown. The streets are designed on a grid system, where lettered streets, A through Z run east to west and numbered streets 1st to 30th run north to south.
    [Show full text]
  • Lesson 2: Circles, Chords, Diameters, and Their Relationships
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M5 GEOMETRY Lesson 2: Circles, Chords, Diameters, and Their Relationships Student Outcomes . Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct the perpendicular bisector of a line segment and draw conclusions about points on that bisector and the endpoints of the segment. They relate the construction to the theorem stating that any perpendicular bisector of a chord must pass through the center of the circle. Classwork Opening Exercise (4 minutes) Scaffolding: Post a diagram and display the steps to create a Opening Exercise perpendicular bisector used in Construct the perpendicular bisector of line segment below (as you did in Module 1). Lesson 4 of Module 1. ���� Label the endpoints of the segment and . Draw circle with center and radius . Draw another line that bisects but is not perpendicular to it. Draw circle with center ���� and radius . List one similarity and one difference���� between the two bisectors. . Label the points of Answers will vary. All points on the perpendicular bisector are equidistant from points and 46T . ���� Points on the other bisector are not equidistant from points A and B. The perpendicular bisector intersection as and . meets at right angles. The other bisector meets at angles that are not congruent. Draw . ���� ⃖����⃗ You may wish to recall for students the definition of equidistant: EQUIDISTANT:. A point is said to be equidistant from two different points and if = . Points and can be replaced in the definition above with other figures (lines, etc.) as long as the distance to those figures is given meaning first.
    [Show full text]
  • Geometry Course Outline Learning Targets Unit 1: Proof, Parallel, And
    Geometry Course Outline Learning Targets Unit 1: Proof, Parallel, and Perpendicular Lines 1-1-1 Identify, describe, and name points, lines, line segments, rays and planes using correct notation. 1-1-2 Identify and name angles. 1-2-1 Describe angles and angle pairs. 1-2-2 Identify and name parts of a circle. 2-1-1 Make conjectures by applying inductive reasoning. 2-1-2 Recognize the limits of inductive reasoning. 2-2-1 Use deductive reasoning to prove that a conjecture is true. 2-2-2 Develop geometric and algebraic arguments based on deductive reasoning. 3-1-1 Distinguish between undefined and defined terms. 3-1-2 Use properties to complete algebraic two-column proofs. 3-2-1 Identify the hypothesis and conclusion of a conditional statement. 3-2-2 Give counterexamples for false conditional statements. 3-3-1 Write and determine the truth value of the converse, inverse, and contrapositive of a conditional statement. 3-3-2 Write and interpret biconditional statements. 4-1-1 Apply the Segment Addition Postulate to find lengths of segments. 4-1-2 Use the definition of midpoint to find lengths of segments. 4-2-1 Apply the Angle Addition Postulate to find angle measures. 4-2-2 Use the definition of angle bisector to find angle measures. 5-1-1 Derive the Distance Formula. 5-1-2 Use the Distance Formula to find the distance between two points on the coordinate plane. 5-2-1 Use inductive reasoning to determine the Midpoint Formula. 5-2-2 Use the Midpoint Formula to find the coordinates of the midpoint of a segment on the coordinate plane.
    [Show full text]