DOCSLIB.ORG

A Possible Solution of Trisection Problem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Possible Solution of Trisection Problem Applied Mathematics in Electrical and Computer Engineering A Possible Solution of Trisection Problem SIAVASH H. SOHRAB Robert McCormick School of Engineering and Applied Science Department of Mechanical Engineering Northwestern University, Evanston, Illinois 60208 [email protected] http://www.mech.northwestern.edu/web/people/faculty/sohrab.php Abstract: - A solution of the ancient Greek problem of trisection of an arbitrary angle employing only compass and straightedge and its algebraic proof are presented. It is shown that while Wantzel’s [1] theory of 1837 concerning irreducibility of the cubic x3 3x 1 0 is correct it does not imply impossibility of trisection of arbitrary angle since rather than a cubic equation the trisection problem is shown to depend on the quadratic equation y2 3 c 0 where c is a constant. The earlier formulation of the problem by Descartes the father of algebraic geometry is also discussed. If one assumes that the ruler and the compass employed in the geometric constructions are in fact Platonic ideal instruments then the trisection solution proposed herein should be exact. Key-Words: The trisection problem, angle trisection, Wantzel theory, regular polygons, heptagon. 1 Introduction The classical trisection problem requires trisecting the algebraic proof of its validity will be presented. an arbitrary angle employing only a compass and a Historically, it was proven by Wantzel [1] that the straightedge or unmarked ruler. The general rules trisection of an arbitrary angle by only compass and concerning the construction instruments and straightedge is impossible if such a construction acceptable solution of the problem are most requires the existence of rational roots of the cubic eloquently described by Dunham [2] equation Indeed, Greek geometers performed trisection (1) by introducing auxiliary curves like the quadratrix of Hippias or the spiral of As described by Dunham [2]: Archimedes, but these curves were not themselves constructible with compass and (a) If we can trisect the general angle with straightedge and thus violated the rules of the compass and straightedge, game. It is rather like reaching the top of o (b) Then we can surely trisect a 60 angle, Everest by helicopter: It achieves the end by an unacceptable means. For a legitimate trisection, (c) So, we can find a constructible solution of only compass and straightedge need apply. , The second rule is that the construction must require only a finite number of steps. (d) So, we can find a rational solution for There must be an end to it. An “infinite , construction,” even if it has trisection as a (e) And this rational solution must be either c/d = 1 limiting outcome, is no good. Construction that goes on forever may be the norm for interstate or c/d = 1. highways, but it is impermissible in geometry. Finally we must devise a procedure to when x is a rational number denoted by the ratio x = trisect any angle. Trisection a particular angle, c/d. Since by Wantzel’s [1] proof (1) is irreducible or even a thousand particular angles, is and (d) is not true then one must conclude that (a) insufficient. If our solution is not general, it is cannot be true. The algebraic equation (1) in not a solution.” Wantzel’s theory [1] originates from the trigonometric equation In this study an unexpectedly simple solution 3 of the ancient Greek trisection problem along with cos 4cos ( / 3) 3cos( / 3) (2) ISBN: 978-1-61804-064-0 277 Applied Mathematics in Electrical and Computer Engineering that when applied to the angle = /3 with similarity between (1) and (6) the failure of Wantzel x 2cos( / 3) results in (1). A cubic equation of [1] to reference the work of Descartes is unfortunate. the form Finally, if parallel to (5) instead of full angle in (2) one applies the trigonometric identity for half angle 3 x qx r 0 (3) 3 cos( / 2) = 4cos ( / 6) 3cos( / 6) (7) was also employed by Descartes [3] in connection and considers = 60 = 3 with one to the trisection problem [4] y2 cos( / 6) arrives at “Descartes dealt with the problem of angle trisection by reducing the problem to a third- y3 3y 3 0 (8) degree equation and constructing it via intersection of circle and parabola” that also does not possess any rational roots. It is interesting to note that cubic equation of the type Descartes proposed a solution of trisection problem by employment of a parabola, a non-constructible x3 b 2 x b 2 c (9) hence transcendental curve, as shown in Fig.1 reproduced from his book of geometry [3] that was first solved by Omar Khayyam using intersection of conics [5] also reduces to (1) and (6) when ( b i 3 , c = 1/3) and ( , c = 1/3), respectively. According to Wantzel’s theory of 1837 [1] only rational numbers x c / d that are roots of algebraic equations are acceptable solution to the trisection problem. This is because the criterion of geometric constructability based on Descartes’s analytic geometry only admits rational operations of addition, subtraction, multiplication, division, and extraction of square roots thus requiring existence of rational roots of polynomials of various degrees [1- 8]. Over three decades after Wantzel’s work Hermite Fig.1 Descartes solution of trisection of an arbitrary (1873) and then Lindemann (1882) respectively angle NOP employing a parabola GAF [3]. proved the existence of transcendental numbers e and [2]. It is known that concerns about basing By geometric construction based on the trisected geometric constructability only on the application of angle shown in Fig.1 Descartes arrived at the cubic geometrical (algebraic) curves and not mechanical equation [3] (transcendental) curves were raised by ancient Greek mathematicians as well as Newton [4]. Clearly, the z3 3z q 0 (4) question of rational versus transcendental numbers could be connected to the admissibility of algebraic where z = NQ and q = NP. It is now clear that for versus transcendental curves as means of geometric = 60 = 3 and a circle of unity radius NO = 1 construction just mentioned. Indeed, in view of the one has NP = q = NO = 1 and both (4) as well as fact that trisecting an angle involves and as was the trigonometric relation emphasized by Gauss transcendental numbers by far are more abundant than rational numbers, it is sin( / 2) = 3sin( / 6) 4sin3 ( / 6) (5) reasonable to anticipate that trisection problem may involve transcendental numbers that are not solutions with the definition z 2sin( / 6) lead to of polynomials with integer coefficients. Therefore Wantzel’s proof may not be applicable to the 3 z 3z 1 0 (6) resolution of trisection problem because this problem involves transcendental numbers and not rational that like (1) has no rational roots. One notes that numbers. In other words, the assumption that only the chord NQ in Fig.1 of Descartes becomes the rational numbers x = c/d should be allowed as unknown NQ = . In view of the acceptable constructible solutions made in steps (c)- ISBN: 978-1-61804-064-0 278 Applied Mathematics in Electrical and Computer Engineering (d) above may not be valid. Such a situation will 2 A Solution of Trisection Problem bex somewhat 2cos( / 3)similar to von Neumann’s proof of Before discussing the trisection problem however, let impossibility of hidden variables in quantum us first examine two different geometric mechanics [9] and the fact that it was later found to configurations that one encounters in the construction be inapplicable to quantum mechanics not because of regular polygons shown schematically in Figs.2a of an error in the theory but rather due to invalid and 2b that were helpful in arriving at the suggested assumptions made in its axiomatic foundation. resolution of trisection problem to be discussed in the Because of the overwhelming abundance of sequel. In Fig.2a the edges of an arbitrary angle AG transcendental numbers there is no reason to are located at points of tangency A and G of the require the root x = 1.879385242… of equation (1) small circles Ri with origins at the vertices of regular to be a rational number. polygons. On the other hand, in Fig.2b the edges of Another important observation concerning the angle GF are located at the position of origins of the classical proof (a)-(e) discussed above is that small circles at points G and F. the term cos on the left hand side of (2) is treated as a constant by substitution for cos( = /3) = ½ while on the right hand side of (2) is treated as the unknown variable that is to be determined. Clearly, such a practice disregards the fact that both the left as well as the right hand sides of the trigonometric equation (2) are in fact functions of the true independent variable of the problem that is the angle . To show how such a practice could influence judgments about constructability one expresses (7) as cos( / 2) (a) 4cos2 ( / 6) 3 (10) cos( / 6) If in the process of geometric construction the ratio on the left hand side of (10) becomes a constant cos( / 2) / cos( / 6) = c for a given angle then one arrives at c y2 3 (11) where y 2cos( / 6). Now, as opposed to the cubic equation (1) the quadratic equation (11) only (b) involves extraction of square root thus making trisection of angle constructible. In fact, once the Fig.2 Two configurations of dividing finite angles into ratio is determined through regular polygons: (a) Integral number of full circles construction the sine of the trisected angle can be (t-o-t-o-t-o-t) versus (b) Two half circles at the directly related to this ratio by noting that (7) could boundaries (o-t-o-t-o-t-o).
Load more

Recommended publications
  • Extending Euclidean Constructions with Dynamic Geometry Software
    Proceedings of the 20th Asian Technology Conference in Mathematics (Leshan, China, 2015) Extending Euclidean constructions with dynamic geometry software Alasdair McAndrew [email protected] College of Engineering and Science Victoria University PO Box 18821, Melbourne 8001 Australia Abstract In order to solve cubic equations by Euclidean means, the standard ruler and compass construction tools are insufficient, as was demonstrated by Pierre Wantzel in the 19th century. However, the ancient Greek mathematicians also used another construction method, the neusis, which was a straightedge with two marked points. We show in this article how a neusis construction can be implemented using dynamic geometry software, and give some examples of its use. 1 Introduction Standard Euclidean geometry, as codified by Euclid, permits of two constructions: drawing a straight line between two given points, and constructing a circle with center at one given point, and passing through another. It can be shown that the set of points constructible by these methods form the quadratic closure of the rationals: that is, the set of all points obtainable by any finite sequence of arithmetic operations and the taking of square roots. With the rise of Galois theory, and of field theory generally in the 19th century, it is now known that irreducible cubic equations cannot be solved by these Euclidean methods: so that the \doubling of the cube", and the \trisection of the angle" problems would need further constructions. Doubling the cube requires us to be able to solve the equation x3 − 2 = 0 and trisecting the angle, if it were possible, would enable us to trisect 60◦ (which is con- structible), to obtain 20◦.
    [Show full text]
  • Es, and (3) Toprovide -Specific Suggestions for Teaching Such Topics
    DOCUMENT RESUME ED 026 236 SE 004 576 Guidelines for Mathematics in the Secondary School South Carolina State Dept. of Education, Columbia. Pub Date 65 Note- I36p. EDRS Price MF-$0.7511C-$6.90 Deseriptors- Advanced Programs, Algebra, Analytic Geometry, Coucse Content, Curriculum,*Curriculum Guides, GeoMetry,Instruction,InstructionalMaterials," *Mathematics, *Number ConCepts,NumberSystems,- *Secondar.. School" Mathematies Identifiers-ISouth Carcilina- This guide containsan outline of topics to be included in individual subject areas in secondary school mathematics andsome specific. suggestions for teachin§ them.. Areas covered inclUde--(1) fundamentals of mathematicsincluded in seventh and eighth grades and general mathematicsin the high school, (2) algebra concepts for COurset one and two, (3) geometry, and (4) advancedmathematics. The guide was written With the following purposes jn mind--(1) to assist local .grOupsto have a basis on which to plan a rykathematics 'course of study,. (2) to give individual teachers an overview of a. particular course Or several cOur:-:es, and (3) toprovide -specific sUggestions for teaching such topics. (RP) Ilia alb 1 fa...4...w. M".7 ,noo d.1.1,64 III.1ai.s3X,i Ala k JS& # Aso sA1.6. It tilatt,41.,,,k a.. -----.-----:--.-:-:-:-:-:-:-:-:-.-. faidel1ae,4 icii MATHEMATICSIN THE SECONDARYSCHOOL Published by STATE DEPARTMENT OF EDUCATION JESSE T. ANDERSON,State Superintendent Columbia, S. C. 1965 Permission to Reprint Permission to reprint A Guide, Mathematics in Florida Second- ary Schools has been granted by the State Department of Edu- cation, Tallahassee, Flmida, Thomas D. Bailey, Superintendent. The South Carolina State Department of Education is in- debted to the Florida State DepartMent of Education and the aahors of A Guide, Mathematics in Florida Secondary Schools.
    [Show full text]
  • Construction Surveying Curves
    Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain.
    [Show full text]
  • And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
    9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ.
    [Show full text]
  • ANCIENT PROBLEMS VS. MODERN TECHNOLOGY 1. Geometric Constructions Some Problems, Such As the Search for a Construction That Woul
    ANCIENT PROBLEMS VS. MODERN TECHNOLOGY SˇARKA´ GERGELITSOVA´ AND TOMA´ Sˇ HOLAN Abstract. Geometric constructions using a ruler and a compass have been known for more than two thousand years. It has also been known for a long time that some problems cannot be solved using the ruler-and-compass method (squaring the circle, angle trisection); on the other hand, there are other prob- lems that are yet to be solved. Nowadays, the focus of researchers’ interest is different: the search for new geometric constructions has shifted to the field of recreational mathematics. In this article, we present the solutions of several construction problems which were discovered with the help of a computer. The aim of this article is to point out that computer availability and perfor- mance have increased to such an extent that, today, anyone can solve problems that have remained unsolved for centuries. 1. Geometric constructions Some problems, such as the search for a construction that would divide a given angle into three equal parts, the construction of a square having an area equal to the area of the given circle or doubling the cube, troubled mathematicians already hundreds and thousands of years ago. Today, we not only know that these problems have never been solved, but we are even able to prove that such constructions cannot exist at all [8], [10]. On the other hand, there is, for example, the problem of finding the center of a given circle with a compass alone. This is a problem that was admired by Napoleon Bonaparte [11] and one of the problems that we are able to solve today (Mascheroni found the answer long ago [9]).
    [Show full text]
  • Construction of Regular Polygons a Constructible Regular Polygon Is One That Can Be Constructed with Compass and (Unmarked) Straightedge
    DynamicsOfPolygons.org Construction of regular polygons A constructible regular polygon is one that can be constructed with compass and (unmarked) straightedge. For example the construction on the right below consists of two circles of equal radii. The center of the second circle at B is chosen to lie anywhere on the first circle, so the triangle ABC is equilateral – and hence equiangular. Compass and straightedge constructions date back to Euclid of Alexandria who was born in about 300 B.C. The Greeks developed methods for constructing the regular triangle, square and pentagon, but these were the only „prime‟ regular polygons that they could construct. They also knew how to double the sides of a given polygon or combine two polygons together – as long as the sides were relatively prime, so a regular pentagon could be drawn together with a regular triangle to get a regular 15-gon. Therefore the polygons they could construct were of the form N = 2m3k5j where m is a nonnegative integer and j and k are either 0 or 1. The constructible regular polygons were 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 32, 40, 48, ... but the only odd polygons in this list are 3,5 and 15. The triangle, pentagon and 15-gon are the only regular polygons with odd sides which the Greeks could construct. If n = p1p2 …pk where the pi are odd primes then n is constructible iff each pi is constructible, so a regular 21-gon can be constructed iff both the triangle and regular 7-gon can be constructed.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • Trisect Angle
    HOW TO TRISECT AN ANGLE (Using P-Geometry) (DRAFT: Liable to change) Aaron Sloman School of Computer Science, University of Birmingham (Philosopher in a Computer Science department) NOTE Added 30 Jan 2020 Remarks on angle-trisection without the neusis construction can be found in Freksa et al. (2019) NOTE Added 1 Mar 2015 The discussion of alternative geometries here contrasts with the discussion of the nature of descriptive metaphysics in "Meta-Descriptive Metaphysics: Extending P.F. Strawson’s ’Descriptive Metaphysics’" http://www.cs.bham.ac.uk/research/projects/cogaff/misc/meta-descriptive-metaphysics.html This document makes connections with the discussion of perception of affordances of various kinds, generalising Gibson’s ideas, in http://www.cs.bham.ac.uk/research/projects/cogaff/talks/#gibson Talk 93: What’s vision for, and how does it work? From Marr (and earlier) to Gibson and Beyond Some of the ideas are related to perception of impossible objects. http://www.cs.bham.ac.uk/research/projects/cogaff/misc/impossible.html JUMP TO CONTENTS Installed: 26 Feb 2015 Last updated: A very nice geogebra applet demonstrates the method described below: http://www.cut-the-knot.org/pythagoras/archi.shtml. Feb 2017: Added note about my 1962 DPhil thesis 25 Apr 2016: Fixed typo: ODB had been mistyped as ODE (Thanks to Michael Fourman) 29 Oct 2015: Added reference to discussion of perception of impossible objects. 4 Oct 2015: Added reference to article by O’Connor and Robertson. 25 Mar 2015: added (low quality) ’movie’ gif showing arrow rotating. 2 Mar 2015 Formatting problem fixed. 1 Mar 2015 Added draft Table of Contents.
    [Show full text]
  • From the Theorem of the Broken Chord to the Beginning of the Trigonometry
    From the Theorem of the Broken Chord to the Beginning of the Trigonometry MARIA DRAKAKI Advisor Professor:Michael Lambrou Department of Mathematics and Applied Mathematics University of Crete May 2020 1/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 1 / 18 Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction.
    [Show full text]
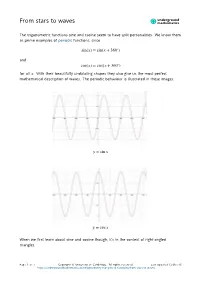
  • From Stars to Waves Mathematics
    underground From stars to waves mathematics The trigonometric functions sine and cosine seem to have split personalities. We know them as prime examples of periodic functions, since sin(푥) = sin(푥 + 360∘) and cos(푥) = cos(푥 + 360∘) for all 푥. With their beautifully undulating shapes they also give us the most perfect mathematical description of waves. The periodic behaviour is illustrated in these images. 푦 = sin 푥 푦 = cos 푥 When we first learn about sine and cosine though, it’s in the context of right-angled triangles. Page 1 of 7 Copyright © University of Cambridge. All rights reserved. Last updated 12-Dec-16 https://undergroundmathematics.org/trigonometry-triangles-to-functions/from-stars-to-waves How do the two representations of these two functions fit together? Imagine looking up at the night sky and try to visualise the stars and planets all lying on a sphere that curves around us, with the Earth at its centre. This is called a celestial sphere. Around 2000 years ago, when early astronomers were trying to chart the night sky, doing astronomy meant doing geometry involving spheres—and that meant being able to do geometry involving circles. Looking at two stars on the celestial sphere, we can ask how far apart they are. We can formulate this as a problem about points on a circle. Given two points 퐴 and 퐵 on a cirle, what is the shortest distance between them, measured along the straight line that lies inside the circle? Such a straight line is called a chord of the circle. Page 2 of 7 Copyright © University of Cambridge.
    [Show full text]
  • Lesson 2: Circles, Chords, Diameters, and Their Relationships
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M5 GEOMETRY Lesson 2: Circles, Chords, Diameters, and Their Relationships Student Outcomes . Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct the perpendicular bisector of a line segment and draw conclusions about points on that bisector and the endpoints of the segment. They relate the construction to the theorem stating that any perpendicular bisector of a chord must pass through the center of the circle. Classwork Opening Exercise (4 minutes) Scaffolding: Post a diagram and display the steps to create a Opening Exercise perpendicular bisector used in Construct the perpendicular bisector of line segment below (as you did in Module 1). Lesson 4 of Module 1. ���� Label the endpoints of the segment and . Draw circle with center and radius . Draw another line that bisects but is not perpendicular to it. Draw circle with center ���� and radius . List one similarity and one difference���� between the two bisectors. . Label the points of Answers will vary. All points on the perpendicular bisector are equidistant from points and 46T . ���� Points on the other bisector are not equidistant from points A and B. The perpendicular bisector intersection as and . meets at right angles. The other bisector meets at angles that are not congruent. Draw . ���� ⃖����⃗ You may wish to recall for students the definition of equidistant: EQUIDISTANT:. A point is said to be equidistant from two different points and if = . Points and can be replaced in the definition above with other figures (lines, etc.) as long as the distance to those figures is given meaning first.
    [Show full text]
  • 11.4 Arcs and Chords
    Page 1 of 5 11.4 Arcs and Chords Goal By finding the perpendicular bisectors of two Use properties of chords of chords, an archaeologist can recreate a whole circles. plate from just one piece. This approach relies on Theorem 11.5, and is Key Words shown in Example 2. • congruent arcs p. 602 • perpendicular bisector p. 274 THEOREM 11.4 B Words If a diameter of a circle is perpendicular to a chord, then the diameter bisects the F chord and its arc. E G Symbols If BG&* ∏ FD&* , then DE&* c EF&* and DGs c GFs. D EXAMPLE 1 Find the Length of a Chord In ᭪C the diameter AF&* is perpendicular to BD&* . D Use the diagram to find the length of BD&* . 5 F C Solution E A Because AF&* is a diameter that is perpendicular to BD&* , you can use Theorem 11.4 to conclude that AF&* bisects B BD&* . So, BE ϭ ED ϭ 5. BD ϭ BE ϩ ED Segment Addition Postulate ϭ 5 ϩ 5 Substitute 5 for BE and ED . ϭ 10 Simplify. ANSWER ᮣ The length of BD&* is 10. Find the Length of a Segment 1. Find the length of JM&* . 2. Find the length of SR&* . H P 12 K C S C M N G 15 P J R 608 Chapter 11 Circles Page 2 of 5 THEOREM 11.5 Words If one chord is a perpendicular bisector M of another chord, then the first chord is a diameter. J P K Symbols If JK&* ∏ ML&* and MP&** c PL&* , then JK&* is a diameter.
    [Show full text]