A New Method of Trisection Archimedes' Method
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Extending Euclidean Constructions with Dynamic Geometry Software
Proceedings of the 20th Asian Technology Conference in Mathematics (Leshan, China, 2015) Extending Euclidean constructions with dynamic geometry software Alasdair McAndrew [email protected] College of Engineering and Science Victoria University PO Box 18821, Melbourne 8001 Australia Abstract In order to solve cubic equations by Euclidean means, the standard ruler and compass construction tools are insufficient, as was demonstrated by Pierre Wantzel in the 19th century. However, the ancient Greek mathematicians also used another construction method, the neusis, which was a straightedge with two marked points. We show in this article how a neusis construction can be implemented using dynamic geometry software, and give some examples of its use. 1 Introduction Standard Euclidean geometry, as codified by Euclid, permits of two constructions: drawing a straight line between two given points, and constructing a circle with center at one given point, and passing through another. It can be shown that the set of points constructible by these methods form the quadratic closure of the rationals: that is, the set of all points obtainable by any finite sequence of arithmetic operations and the taking of square roots. With the rise of Galois theory, and of field theory generally in the 19th century, it is now known that irreducible cubic equations cannot be solved by these Euclidean methods: so that the \doubling of the cube", and the \trisection of the angle" problems would need further constructions. Doubling the cube requires us to be able to solve the equation x3 − 2 = 0 and trisecting the angle, if it were possible, would enable us to trisect 60◦ (which is con- structible), to obtain 20◦. -

Es, and (3) Toprovide -Specific Suggestions for Teaching Such Topics
DOCUMENT RESUME ED 026 236 SE 004 576 Guidelines for Mathematics in the Secondary School South Carolina State Dept. of Education, Columbia. Pub Date 65 Note- I36p. EDRS Price MF-$0.7511C-$6.90 Deseriptors- Advanced Programs, Algebra, Analytic Geometry, Coucse Content, Curriculum,*Curriculum Guides, GeoMetry,Instruction,InstructionalMaterials," *Mathematics, *Number ConCepts,NumberSystems,- *Secondar.. School" Mathematies Identifiers-ISouth Carcilina- This guide containsan outline of topics to be included in individual subject areas in secondary school mathematics andsome specific. suggestions for teachin§ them.. Areas covered inclUde--(1) fundamentals of mathematicsincluded in seventh and eighth grades and general mathematicsin the high school, (2) algebra concepts for COurset one and two, (3) geometry, and (4) advancedmathematics. The guide was written With the following purposes jn mind--(1) to assist local .grOupsto have a basis on which to plan a rykathematics 'course of study,. (2) to give individual teachers an overview of a. particular course Or several cOur:-:es, and (3) toprovide -specific sUggestions for teaching such topics. (RP) Ilia alb 1 fa...4...w. M".7 ,noo d.1.1,64 III.1ai.s3X,i Ala k JS& # Aso sA1.6. It tilatt,41.,,,k a.. -----.-----:--.-:-:-:-:-:-:-:-:-.-. faidel1ae,4 icii MATHEMATICSIN THE SECONDARYSCHOOL Published by STATE DEPARTMENT OF EDUCATION JESSE T. ANDERSON,State Superintendent Columbia, S. C. 1965 Permission to Reprint Permission to reprint A Guide, Mathematics in Florida Second- ary Schools has been granted by the State Department of Edu- cation, Tallahassee, Flmida, Thomas D. Bailey, Superintendent. The South Carolina State Department of Education is in- debted to the Florida State DepartMent of Education and the aahors of A Guide, Mathematics in Florida Secondary Schools. -
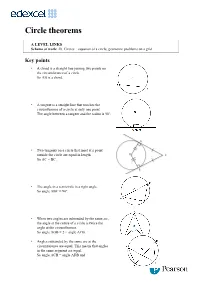
Circle Theorems
Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°. -

ANCIENT PROBLEMS VS. MODERN TECHNOLOGY 1. Geometric Constructions Some Problems, Such As the Search for a Construction That Woul
ANCIENT PROBLEMS VS. MODERN TECHNOLOGY SˇARKA´ GERGELITSOVA´ AND TOMA´ Sˇ HOLAN Abstract. Geometric constructions using a ruler and a compass have been known for more than two thousand years. It has also been known for a long time that some problems cannot be solved using the ruler-and-compass method (squaring the circle, angle trisection); on the other hand, there are other prob- lems that are yet to be solved. Nowadays, the focus of researchers’ interest is different: the search for new geometric constructions has shifted to the field of recreational mathematics. In this article, we present the solutions of several construction problems which were discovered with the help of a computer. The aim of this article is to point out that computer availability and perfor- mance have increased to such an extent that, today, anyone can solve problems that have remained unsolved for centuries. 1. Geometric constructions Some problems, such as the search for a construction that would divide a given angle into three equal parts, the construction of a square having an area equal to the area of the given circle or doubling the cube, troubled mathematicians already hundreds and thousands of years ago. Today, we not only know that these problems have never been solved, but we are even able to prove that such constructions cannot exist at all [8], [10]. On the other hand, there is, for example, the problem of finding the center of a given circle with a compass alone. This is a problem that was admired by Napoleon Bonaparte [11] and one of the problems that we are able to solve today (Mascheroni found the answer long ago [9]). -

Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis. -

Construction of Regular Polygons a Constructible Regular Polygon Is One That Can Be Constructed with Compass and (Unmarked) Straightedge
DynamicsOfPolygons.org Construction of regular polygons A constructible regular polygon is one that can be constructed with compass and (unmarked) straightedge. For example the construction on the right below consists of two circles of equal radii. The center of the second circle at B is chosen to lie anywhere on the first circle, so the triangle ABC is equilateral – and hence equiangular. Compass and straightedge constructions date back to Euclid of Alexandria who was born in about 300 B.C. The Greeks developed methods for constructing the regular triangle, square and pentagon, but these were the only „prime‟ regular polygons that they could construct. They also knew how to double the sides of a given polygon or combine two polygons together – as long as the sides were relatively prime, so a regular pentagon could be drawn together with a regular triangle to get a regular 15-gon. Therefore the polygons they could construct were of the form N = 2m3k5j where m is a nonnegative integer and j and k are either 0 or 1. The constructible regular polygons were 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 32, 40, 48, ... but the only odd polygons in this list are 3,5 and 15. The triangle, pentagon and 15-gon are the only regular polygons with odd sides which the Greeks could construct. If n = p1p2 …pk where the pi are odd primes then n is constructible iff each pi is constructible, so a regular 21-gon can be constructed iff both the triangle and regular 7-gon can be constructed. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Trisect Angle
HOW TO TRISECT AN ANGLE (Using P-Geometry) (DRAFT: Liable to change) Aaron Sloman School of Computer Science, University of Birmingham (Philosopher in a Computer Science department) NOTE Added 30 Jan 2020 Remarks on angle-trisection without the neusis construction can be found in Freksa et al. (2019) NOTE Added 1 Mar 2015 The discussion of alternative geometries here contrasts with the discussion of the nature of descriptive metaphysics in "Meta-Descriptive Metaphysics: Extending P.F. Strawson’s ’Descriptive Metaphysics’" http://www.cs.bham.ac.uk/research/projects/cogaff/misc/meta-descriptive-metaphysics.html This document makes connections with the discussion of perception of affordances of various kinds, generalising Gibson’s ideas, in http://www.cs.bham.ac.uk/research/projects/cogaff/talks/#gibson Talk 93: What’s vision for, and how does it work? From Marr (and earlier) to Gibson and Beyond Some of the ideas are related to perception of impossible objects. http://www.cs.bham.ac.uk/research/projects/cogaff/misc/impossible.html JUMP TO CONTENTS Installed: 26 Feb 2015 Last updated: A very nice geogebra applet demonstrates the method described below: http://www.cut-the-knot.org/pythagoras/archi.shtml. Feb 2017: Added note about my 1962 DPhil thesis 25 Apr 2016: Fixed typo: ODB had been mistyped as ODE (Thanks to Michael Fourman) 29 Oct 2015: Added reference to discussion of perception of impossible objects. 4 Oct 2015: Added reference to article by O’Connor and Robertson. 25 Mar 2015: added (low quality) ’movie’ gif showing arrow rotating. 2 Mar 2015 Formatting problem fixed. 1 Mar 2015 Added draft Table of Contents. -

Classify Each Triangle by Its Side Lengths and Angle Measurements
GRADE 4 | MODULE 4 | TOPIC D | LESSONS 12–16 KEY CONCEPT OVERVIEW In Lessons 12 through 16, students explore lines of symmetry and characteristics of triangles and quadrilaterals. You can expect to see homework that asks your child to do the following: ▪ Find and draw lines of symmetry. ▪ Given half of a figure and the line of symmetry, draw the other half of the figure. ▪ Classify triangles by side lengths (e.g., equilateral, isosceles, scalene) and by angle measurements (e.g., acute, right, obtuse). ▪ Draw triangles that fit different classifications (e.g., acute and scalene). ▪ Name quadrilaterals, identify attributes (i.e., characteristics) that define them, and construct them based on given attributes. SAMPLE PROBLEM (From Lesson 13) Classify each triangle by its side lengths and angle measurements. Circle the correct names. Additional sample problems with detailed answer steps are found in the Eureka Math Homework Helpers books. Learn more at GreatMinds.org. For more resources, visit » Eureka.support GRADE 4 | MODULE 4 | TOPIC D | LESSONS 12–16 HOW YOU CAN HELP AT HOME ▪ Ask your child to look around the house for objects that have lines of symmetry. Examples include the headboard of a bed, dressers, chairs, couches, and place mats. Ask him to show where the line of symmetry would be and what makes it a line of symmetry. Be careful of objects such as doors and windows. They could have a line of symmetry, but if there’s a knob or crank on just one side, then they are not symmetrical. ▪ Ask your child to name and draw all the quadrilaterals she can think of (e.g., square, rectangle, parallelogram, trapezoid, and rhombus). -

Trisecting an Angle and Doubling the Cube Using Origami Method
広 島 経 済 大 学 研 究 論 集 第38巻第 4 号 2016年 3 月 Note Trisecting an Angle and Doubling the Cube Using Origami Method Kenji Hiraoka* and Laura Kokot** meaning to fold, and kami meaning paper, refers 1. Introduction to the traditional art of making various attractive Laura Kokot, one of the authors, Mathematics and decorative figures using only one piece of and Computer Science teacher in the High school square sheet of paper. This art is very popular, of Mate Blažine Labin, Croatia came to Nagasaki, not only in Japan, but also in other countries all Japan in October 2014, for the teacher training over the world and everyone knows about the program at the Nagasaki University as a MEXT paper crane which became the international (Ministry of education, culture, sports, science symbol of peace. Origami as a form is continu- and technology) scholar. Her training program ously evolving and nowadays a lot of other was conducted at the Faculty of Education, possibilities and benefits of origami are being Nagasaki University in the field of Mathematics recognized. For example in education and other. Education under Professor Hiraoka Kenji. The goal of this paper is to research and For every teacher it is important that pupils learn more about geometric constructions by in his class understand and learn the material as using origami method and its properties as an easily as possible and he will try to find the best alternative approach to learning and teaching pedagogical approaches in his teaching. It is not high school geometry. -

ASIA-EUROPE CLASSROOM NETWORK (AEC-NET) Title: “Famous Mathematicians in Greece”
ASIA-EUROPE CLASSROOM NETWORK (AEC-NET) Title: “Famous Mathematicians in Greece” Participant students: Barbakou C., Dikaiakos X., Karali C., Karanikolas N., Katsouli J., Kefalas G., Mixailidis M., Xifaras N. Teacher coordinator: Efstathiou M. S. Avgoulea – Linardatou High school Some information about our School Our school was first established by Ms Stavroula Avgoulea-Linardatou in 1949, when she was still only 23, indeed at the end of an overwhelming and annihilating decade for Greece. Her vision was to create a school which would utilize novel and innovative teaching ways in order to promote the students’ learning and Nowadays, after over 60 years, our school has creative skills while at the same time become an educational organisation which covers all boost their self-esteem and education stages from nursery school to upper- confidence, thus leading towards the secondary school, with about 1.400 students and effortless acquisition of knowledge 260 employees. Since 1991 Mr. George Linardatos, and the building of a complete and the son of the school’s founder, has taken over the sound personality. management of the school, which, besides being a source of knowledge, also promotes cultural sensitisation and educational innovation. A. PROJECT DESCRIPTION/ SUMMARY We investigate, within Greece, what famous mathematicians there are and we describe their contribution to Mathematics. This power point will be further developed by students investigating mathematicians in another country, not participating in the project. The project will be finished off with a chat, where we take part in international teams and answer a quiz, by using G-mail and its chattforum. B. INTRODUCTION The ancient Greeks were very interested in scientific thought. -
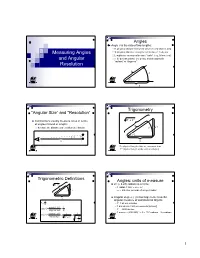
Measuring Angles and Angular Resolution
Angles Angle θ is the ratio of two lengths: R: physical distance between observer and objects [km] Measuring Angles S: physical distance along the arc between 2 objects Lengths are measured in same “units” (e.g., kilometers) and Angular θ is “dimensionless” (no units), and measured in “radians” or “degrees” Resolution R S θ R Trigonometry “Angular Size” and “Resolution” 22 Astronomers usually measure sizes in terms R +Y of angles instead of lengths R because the distances are seldom well known S Y θ θ S R R S = physical length of the arc, measured in m Y = physical length of the vertical side [m] Trigonometric Definitions Angles: units of measure R22+Y 2π (≈ 6.28) radians in a circle R 1 radian = 360˚ ÷ 2π≈57 ˚ S Y ⇒≈206,265 seconds of arc per radian θ Angular degree (˚) is too large to be a useful R S angular measure of astronomical objects θ ≡ R 1º = 60 arc minutes opposite side Y 1 arc minute = 60 arc seconds [arcsec] tan[]θ ≡= adjacent side R 1º = 3600 arcsec -1 -6 opposite sideY 1 1 arcsec ≈ (206,265) ≈ 5 × 10 radians = 5 µradians sin[]θ ≡== hypotenuse RY22+ R 2 1+ Y 2 1 Number of Degrees per Radian Trigonometry in Astronomy Y 2π radians per circle θ S R 360° Usually R >> S (particularly in astronomy), so Y ≈ S 1 radian = ≈ 57.296° 2π SY Y 1 θ ≡≈≈ ≈ ≈ 57° 17'45" RR RY22+ R 2 1+ Y 2 θ ≈≈tan[θθ] sin[ ] Relationship of Trigonometric sin[θ ] ≈ tan[θ ] ≈ θ for θ ≈ 0 Functions for Small Angles 1 sin(πx) Check it! tan(πx) 0.5 18˚ = 18˚ × (2π radians per circle) ÷ (360˚ per πx circle) = 0.1π radians ≈ 0.314 radians 0 Calculated Results