The Evolution of the Geometer's Sketchpad Daniel Scher
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture 3 1 Geometry of Linear Programs
ORIE 6300 Mathematical Programming I September 2, 2014 Lecture 3 Lecturer: David P. Williamson Scribe: Divya Singhvi Last time we discussed how to take dual of an LP in two different ways. Today we will talk about the geometry of linear programs. 1 Geometry of Linear Programs First we need some definitions. Definition 1 A set S ⊆ <n is convex if 8x; y 2 S, λx + (1 − λ)y 2 S, 8λ 2 [0; 1]. Figure 1: Examples of convex and non convex sets Given a set of inequalities we define the feasible region as P = fx 2 <n : Ax ≤ bg. We say that P is a polyhedron. Which points on this figure can have the optimal value? Our intuition from last time is that Figure 2: Example of a polyhedron. \Circled" corners are feasible and \squared" are non feasible optimal solutions to linear programming problems occur at \corners" of the feasible region. What we'd like to do now is to consider formal definitions of the \corners" of the feasible region. 3-1 One idea is that a point in the polyhedron is a corner if there is some objective function that is minimized there uniquely. Definition 2 x 2 P is a vertex of P if 9c 2 <n with cT x < cT y; 8y 6= x; y 2 P . Another idea is that a point x 2 P is a corner if there are no small perturbations of x that are in P . Definition 3 Let P be a convex set in <n. Then x 2 P is an extreme point of P if x cannot be written as λy + (1 − λ)z for y; z 2 P , y; z 6= x, 0 ≤ λ ≤ 1. -

Archimedean Solids
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat). -

Chapter 5 Dimensional Analysis and Similarity
Chapter 5 Dimensional Analysis and Similarity Motivation. In this chapter we discuss the planning, presentation, and interpretation of experimental data. We shall try to convince you that such data are best presented in dimensionless form. Experiments which might result in tables of output, or even mul- tiple volumes of tables, might be reduced to a single set of curves—or even a single curve—when suitably nondimensionalized. The technique for doing this is dimensional analysis. Chapter 3 presented gross control-volume balances of mass, momentum, and en- ergy which led to estimates of global parameters: mass flow, force, torque, total heat transfer. Chapter 4 presented infinitesimal balances which led to the basic partial dif- ferential equations of fluid flow and some particular solutions. These two chapters cov- ered analytical techniques, which are limited to fairly simple geometries and well- defined boundary conditions. Probably one-third of fluid-flow problems can be attacked in this analytical or theoretical manner. The other two-thirds of all fluid problems are too complex, both geometrically and physically, to be solved analytically. They must be tested by experiment. Their behav- ior is reported as experimental data. Such data are much more useful if they are ex- pressed in compact, economic form. Graphs are especially useful, since tabulated data cannot be absorbed, nor can the trends and rates of change be observed, by most en- gineering eyes. These are the motivations for dimensional analysis. The technique is traditional in fluid mechanics and is useful in all engineering and physical sciences, with notable uses also seen in the biological and social sciences. -
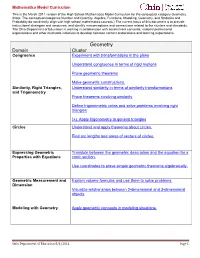
High School Geometry Model Curriculum Math.Pdf
Mathematics Model Curriculum This is the March 2011 version of the High School Mathematics Model Curriculum for the conceptual category Geometry. (Note: The conceptual categories Number and Quantity, Algebra, Functions, Modeling, Geometry, and Statistics and Probability do not directly align with high school mathematics courses.) The current focus of this document is to provide instructional strategies and resources, and identify misconceptions and connections related to the clusters and standards. The Ohio Department of Education is working in collaboration with assessment consortia, national professional organizations and other multistate initiatives to develop common content elaborations and learning expectations. Geometry Domain Cluster Congruence Experiment with transformations in the plane Understand congruence in terms of rigid motions Prove geometric theorems Make geometric constructions. Similarity, Right Triangles, Understand similarity in terms of similarity transformations and Trigonometry Prove theorems involving similarity Define trigonometric ratios and solve problems involving right triangles (+) Apply trigonometry to general triangles Circles Understand and apply theorems about circles. Find arc lengths and areas of sectors of circles. Expressing Geometric Translate between the geometric description and the equation for a Properties with Equations conic section. Use coordinates to prove simple geometric theorems algebraically. Geometric Measurement and Explain volume formulas and use them to solve problems. Dimension -
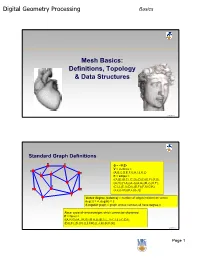
Digital Geometry Processing Mesh Basics
Digital Geometry Processing Basics Mesh Basics: Definitions, Topology & Data Structures 1 © Alla Sheffer Standard Graph Definitions G = <V,E> V = vertices = {A,B,C,D,E,F,G,H,I,J,K,L} E = edges = {(A,B),(B,C),(C,D),(D,E),(E,F),(F,G), (G,H),(H,A),(A,J),(A,G),(B,J),(K,F), (C,L),(C,I),(D,I),(D,F),(F,I),(G,K), (J,L),(J,K),(K,L),(L,I)} Vertex degree (valence) = number of edges incident on vertex deg(J) = 4, deg(H) = 2 k-regular graph = graph whose vertices all have degree k Face: cycle of vertices/edges which cannot be shortened F = faces = {(A,H,G),(A,J,K,G),(B,A,J),(B,C,L,J),(C,I,L),(C,D,I), (D,E,F),(D,I,F),(L,I,F,K),(L,J,K),(K,F,G)} © Alla Sheffer Page 1 Digital Geometry Processing Basics Connectivity Graph is connected if there is a path of edges connecting every two vertices Graph is k-connected if between every two vertices there are k edge-disjoint paths Graph G’=<V’,E’> is a subgraph of graph G=<V,E> if V’ is a subset of V and E’ is the subset of E incident on V’ Connected component of a graph: maximal connected subgraph Subset V’ of V is an independent set in G if the subgraph it induces does not contain any edges of E © Alla Sheffer Graph Embedding Graph is embedded in Rd if each vertex is assigned a position in Rd Embedding in R2 Embedding in R3 © Alla Sheffer Page 2 Digital Geometry Processing Basics Planar Graphs Planar Graph Plane Graph Planar graph: graph whose vertices and edges can Straight Line Plane Graph be embedded in R2 such that its edges do not intersect Every planar graph can be drawn as a straight-line plane graph © -

The Development of Thales Theorem Throughout History Slim Mrabet
The development of Thales theorem throughout history Slim Mrabet To cite this version: Slim Mrabet. The development of Thales theorem throughout history. Eleventh Congress of the European Society for Research in Mathematics Education, Utrecht University, Feb 2019, Utrecht, Netherlands. hal-02421913 HAL Id: hal-02421913 https://hal.archives-ouvertes.fr/hal-02421913 Submitted on 20 Dec 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The development of Thales theorem throughout history Slim MRABET Carthage University, Tunisia; [email protected] Keywords: Thales theorem, similar triangles, transformation. Thales theorem may have different functionalities when using distances, algebraic measurements, or vectors. In addition to that, the utilization of a figure formed of secant lines and parallels or a figure relating to two similar triangles. The aim of this work is to categorize different formulations of Thales theorem and explain why in teaching we must know the appropriate mathematical environment related to each Thales Theorem statement. The analysis of many geometry books in history makes it possible to distinguish two points of view according to different forms, demonstrations and applications of this concept. The Euclidean point of view The general statement of Thales theorem shows us the idea to move from one triangle to another, moreover, the link with similar triangles (immediately following it and generally with similar figures) is a characteristic of this point of view. -

Geometry Course Outline
GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid -

Similar Quadrilaterals Cui, Kadaveru, Lee, Maheshwari Page 1
Similar Quadrilaterals Cui, Kadaveru, Lee, Maheshwari Page 1 Similar Quadrilaterals Authors Guangqi Cui, Akshaj Kadaveru, Joshua Lee, Sagar Maheshwari Special thanks to Cosmin Pohoata and the AMSP Cornell 2014 Geometric Proofs Class B0 C0 B A A0 D0 C D Additional thanks to Justin Stevens and David Altizio for the LATEX Template Similar Quadrilaterals Cui, Kadaveru, Lee, Maheshwari Page 2 Contents 1 Introduction 3 2 Interesting Property 4 3 Example Problems 5 4 Practice Problems 11 Similar Quadrilaterals Cui, Kadaveru, Lee, Maheshwari Page 3 1 Introduction Similar quadrilaterals are a very useful but relatively unknown tool used to solve olympiad geometry problems. It usually goes unnoticed due to the confinement of geometric education to the geometry of the triangle and other conventional methods of problem solving. Also, it is only in very special cases where pairs of similar quadrilaterals exist, and proofs using these qualities usually shorten what would have otherwise been an unnecessarily long proof. The most common method of finding such quadrilaterals involves finding one pair of adjacent sides with identical ratios, and three pairs of congruent angles. We will call this SSAAA Similarity. 0 0 0 0 Example 1.1. (SSAAA Similarity) Two quadrilaterals ABCD and A B C D satisfy \A = AB BC A0, B = B0, C = C0, and = . Show that ABCD and A0B0C0D0 are similar. \ \ \ \ \ A0B0 B0C0 B0 C0 B A A0 D0 C D 0 0 0 0 0 0 Solution. Notice 4ABC and 4A B C are similar from SAS similarity. Therefore \C A D = 0 0 0 0 0 0 0 0 0 0 \A − \B A C = \A − \BAC = \CAD. -

∆ Congruence & Similarity
www.MathEducationPage.org Henri Picciotto Triangle Congruence and Similarity A Common-Core-Compatible Approach Henri Picciotto The Common Core State Standards for Mathematics (CCSSM) include a fundamental change in the geometry program in grades 8 to 10: geometric transformations, not congruence and similarity postulates, are to constitute the logical foundation of geometry at this level. This paper proposes an approach to triangle congruence and similarity that is compatible with this new vision. Transformational Geometry and the Common Core From the CCSSM1: The concepts of congruence, similarity, and symmetry can be understood from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combinations of these, all of which are here assumed to preserve distance and angles (and therefore shapes generally). Reflections and rotations each explain a particular type of symmetry, and the symmetries of an object offer insight into its attributes—as when the reflective symmetry of an isosceles triangle assures that its base angles are congruent. In the approach taken here, two geometric figures are defined to be congruent if there is a sequence of rigid motions that carries one onto the other. This is the principle of superposition. For triangles, congruence means the equality of all corresponding pairs of sides and all corresponding pairs of angles. During the middle grades, through experiences drawing triangles from given conditions, students notice ways to specify enough measures in a triangle to ensure that all triangles drawn with those measures are congruent. Once these triangle congruence criteria (ASA, SAS, and SSS) are established using rigid motions, they can be used to prove theorems about triangles, quadrilaterals, and other geometric figures. -

15 BASIC PROPERTIES of CONVEX POLYTOPES Martin Henk, J¨Urgenrichter-Gebert, and G¨Unterm
15 BASIC PROPERTIES OF CONVEX POLYTOPES Martin Henk, J¨urgenRichter-Gebert, and G¨unterM. Ziegler INTRODUCTION Convex polytopes are fundamental geometric objects that have been investigated since antiquity. The beauty of their theory is nowadays complemented by their im- portance for many other mathematical subjects, ranging from integration theory, algebraic topology, and algebraic geometry to linear and combinatorial optimiza- tion. In this chapter we try to give a short introduction, provide a sketch of \what polytopes look like" and \how they behave," with many explicit examples, and briefly state some main results (where further details are given in subsequent chap- ters of this Handbook). We concentrate on two main topics: • Combinatorial properties: faces (vertices, edges, . , facets) of polytopes and their relations, with special treatments of the classes of low-dimensional poly- topes and of polytopes \with few vertices;" • Geometric properties: volume and surface area, mixed volumes, and quer- massintegrals, including explicit formulas for the cases of the regular simplices, cubes, and cross-polytopes. We refer to Gr¨unbaum [Gr¨u67]for a comprehensive view of polytope theory, and to Ziegler [Zie95] respectively to Gruber [Gru07] and Schneider [Sch14] for detailed treatments of the combinatorial and of the convex geometric aspects of polytope theory. 15.1 COMBINATORIAL STRUCTURE GLOSSARY d V-polytope: The convex hull of a finite set X = fx1; : : : ; xng of points in R , n n X i X P = conv(X) := λix λ1; : : : ; λn ≥ 0; λi = 1 : i=1 i=1 H-polytope: The solution set of a finite system of linear inequalities, d T P = P (A; b) := x 2 R j ai x ≤ bi for 1 ≤ i ≤ m ; with the extra condition that the set of solutions is bounded, that is, such that m×d there is a constant N such that jjxjj ≤ N holds for all x 2 P . -

Frequently Asked Questions in Polyhedral Computation
Frequently Asked Questions in Polyhedral Computation http://www.ifor.math.ethz.ch/~fukuda/polyfaq/polyfaq.html Komei Fukuda Swiss Federal Institute of Technology Lausanne and Zurich, Switzerland [email protected] Version June 18, 2004 Contents 1 What is Polyhedral Computation FAQ? 2 2 Convex Polyhedron 3 2.1 What is convex polytope/polyhedron? . 3 2.2 What are the faces of a convex polytope/polyhedron? . 3 2.3 What is the face lattice of a convex polytope . 4 2.4 What is a dual of a convex polytope? . 4 2.5 What is simplex? . 4 2.6 What is cube/hypercube/cross polytope? . 5 2.7 What is simple/simplicial polytope? . 5 2.8 What is 0-1 polytope? . 5 2.9 What is the best upper bound of the numbers of k-dimensional faces of a d- polytope with n vertices? . 5 2.10 What is convex hull? What is the convex hull problem? . 6 2.11 What is the Minkowski-Weyl theorem for convex polyhedra? . 6 2.12 What is the vertex enumeration problem, and what is the facet enumeration problem? . 7 1 2.13 How can one enumerate all faces of a convex polyhedron? . 7 2.14 What computer models are appropriate for the polyhedral computation? . 8 2.15 How do we measure the complexity of a convex hull algorithm? . 8 2.16 How many facets does the average polytope with n vertices in Rd have? . 9 2.17 How many facets can a 0-1 polytope with n vertices in Rd have? . 10 2.18 How hard is it to verify that an H-polyhedron PH and a V-polyhedron PV are equal? . -

Points, Lines, and Planes a Point Is a Position in Space. a Point Has No Length Or Width Or Thickness
Points, Lines, and Planes A Point is a position in space. A point has no length or width or thickness. A point in geometry is represented by a dot. To name a point, we usually use a (capital) letter. A A (straight) line has length but no width or thickness. A line is understood to extend indefinitely to both sides. It does not have a beginning or end. A B C D A line consists of infinitely many points. The four points A, B, C, D are all on the same line. Postulate: Two points determine a line. We name a line by using any two points on the line, so the above line can be named as any of the following: ! ! ! ! ! AB BC AC AD CD Any three or more points that are on the same line are called colinear points. In the above, points A; B; C; D are all colinear. A Ray is part of a line that has a beginning point, and extends indefinitely to one direction. A B C D A ray is named by using its beginning point with another point it contains. −! −! −−! −−! In the above, ray AB is the same ray as AC or AD. But ray BD is not the same −−! ray as AD. A (line) segment is a finite part of a line between two points, called its end points. A segment has a finite length. A B C D B C In the above, segment AD is not the same as segment BC Segment Addition Postulate: In a line segment, if points A; B; C are colinear and point B is between point A and point C, then AB + BC = AC You may look at the plus sign, +, as adding the length of the segments as numbers.