Mathematical Writing by Donald E
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Trinity College Bulletin, March 1952
TRINITY COLLEGE BULLETIN ALUMNI NEWS ISSUE • MARCH, 1952 • HARTFORD, CONNECTICUT IN THIS ISSUE T. H. Bissonnette A M emorial Cooper and Downs on History ..... Alumni Notes by the Class Secretaries Best Sports Story of 1951 Hell Week Out Profiles of Professors Costello, Harrington Goralski Improves A T rinity student as caricatured by the Chapel architect on a misericord arm in the chancel. George Capen Says.· During the past few days, I have analyzed this year's Alumni Fund, now at 33,500. Frankly, while I am not disheartened, the results so far are not encouraging. When the National Alumni Association accepted on behal f of all the alumni a goal of $50,000, it was done because we knew that all alumni realize the importance to Trinity of an outstanding faculty. We knew, too, that a successful campaign would depend on these two factors: ( 1) Increased contributions from those alumni who have given in the past, and ( 2) contributions from the large number of alumni who had not contributed previously. The increases are just not coming through, and the rate of new contributors is very disappointing. However, a cheering trend is the fine showing of our younger alumni, those of the Classes of '49, '50, and '51. I know that Trinity alumni are interested in the faculty both because of the importance of good teaching at the college and also in recognition of their own personal appreciation of the men still at Trinity who taught them. But we are going to have to do a lot better in this Alumni Fund if the increases in faculty salaries given last Sep tember are to be covered. -

Donald Knuth Fletcher Jones Professor of Computer Science, Emeritus Curriculum Vitae Available Online
Donald Knuth Fletcher Jones Professor of Computer Science, Emeritus Curriculum Vitae available Online Bio BIO Donald Ervin Knuth is an American computer scientist, mathematician, and Professor Emeritus at Stanford University. He is the author of the multi-volume work The Art of Computer Programming and has been called the "father" of the analysis of algorithms. He contributed to the development of the rigorous analysis of the computational complexity of algorithms and systematized formal mathematical techniques for it. In the process he also popularized the asymptotic notation. In addition to fundamental contributions in several branches of theoretical computer science, Knuth is the creator of the TeX computer typesetting system, the related METAFONT font definition language and rendering system, and the Computer Modern family of typefaces. As a writer and scholar,[4] Knuth created the WEB and CWEB computer programming systems designed to encourage and facilitate literate programming, and designed the MIX/MMIX instruction set architectures. As a member of the academic and scientific community, Knuth is strongly opposed to the policy of granting software patents. He has expressed his disagreement directly to the patent offices of the United States and Europe. (via Wikipedia) ACADEMIC APPOINTMENTS • Professor Emeritus, Computer Science HONORS AND AWARDS • Grace Murray Hopper Award, ACM (1971) • Member, American Academy of Arts and Sciences (1973) • Turing Award, ACM (1974) • Lester R Ford Award, Mathematical Association of America (1975) • Member, National Academy of Sciences (1975) 5 OF 44 PROFESSIONAL EDUCATION • PhD, California Institute of Technology , Mathematics (1963) PATENTS • Donald Knuth, Stephen N Schiller. "United States Patent 5,305,118 Methods of controlling dot size in digital half toning with multi-cell threshold arrays", Adobe Systems, Apr 19, 1994 • Donald Knuth, LeRoy R Guck, Lawrence G Hanson. -
![Positional Notation Or Trigonometry [2, 13]](https://docslib.b-cdn.net/cover/6799/positional-notation-or-trigonometry-2-13-106799.webp)
Positional Notation Or Trigonometry [2, 13]
The Greatest Mathematical Discovery? David H. Bailey∗ Jonathan M. Borweiny April 24, 2011 1 Introduction Question: What mathematical discovery more than 1500 years ago: • Is one of the greatest, if not the greatest, single discovery in the field of mathematics? • Involved three subtle ideas that eluded the greatest minds of antiquity, even geniuses such as Archimedes? • Was fiercely resisted in Europe for hundreds of years after its discovery? • Even today, in historical treatments of mathematics, is often dismissed with scant mention, or else is ascribed to the wrong source? Answer: Our modern system of positional decimal notation with zero, to- gether with the basic arithmetic computational schemes, which were discov- ered in India prior to 500 CE. ∗Bailey: Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. Email: [email protected]. This work was supported by the Director, Office of Computational and Technology Research, Division of Mathematical, Information, and Computational Sciences of the U.S. Department of Energy, under contract number DE-AC02-05CH11231. yCentre for Computer Assisted Research Mathematics and its Applications (CARMA), University of Newcastle, Callaghan, NSW 2308, Australia. Email: [email protected]. 1 2 Why? As the 19th century mathematician Pierre-Simon Laplace explained: It is India that gave us the ingenious method of expressing all numbers by means of ten symbols, each symbol receiving a value of position as well as an absolute value; a profound and important idea which appears so simple to us now that we ignore its true merit. But its very sim- plicity and the great ease which it has lent to all computations put our arithmetic in the first rank of useful inventions; and we shall appre- ciate the grandeur of this achievement the more when we remember that it escaped the genius of Archimedes and Apollonius, two of the greatest men produced by antiquity. -

Knuthweb.Pdf
Literate Programming Donald E. Knuth Computer Science Department, Stanford University, Stanford, CA 94305, USA The author and his associates have been experimenting for the past several years with a program- ming language and documentation system called WEB. This paper presents WEB by example, and discusses why the new system appears to be an improvement over previous ones. I would ordinarily have assigned to student research A. INTRODUCTION assistants; and why? Because it seems to me that at last I’m able to write programs as they should be written. The past ten years have witnessed substantial improve- My programs are not only explained better than ever ments in programming methodology. This advance, before; they also are better programs, because the new carried out under the banner of “structured program- methodology encourages me to do a better job. For ming,” has led to programs that are more reliable and these reasons I am compelled to write this paper, in easier to comprehend; yet the results are not entirely hopes that my experiences will prove to be relevant to satisfactory. My purpose in the present paper is to others. propose another motto that may be appropriate for the I must confess that there may also be a bit of mal- next decade, as we attempt to make further progress ice in my choice of a title. During the 1970s I was in the state of the art. I believe that the time is ripe coerced like everybody else into adopting the ideas of for significantly better documentation of programs, and structured programming, because I couldn’t bear to be that we can best achieve this by considering programs found guilty of writing unstructured programs. -

On-The-Fly Garbage Collection: an Exercise in Cooperation
8. HoIn, B.K.P. Determining lightness from an image. Comptr. Graphics and Image Processing 3, 4(Dec. 1974), 277-299. 9. Huffman, D.A. Impossible objects as nonsense sentences. In Machine Intelligence 6, B. Meltzer and D. Michie, Eds., Edinburgh U. Press, Edinburgh, 1971, pp. 295-323. 10. Mackworth, A.K. Consistency in networks of relations. Artif. Intell. 8, 1(1977), 99-118. I1. Marr, D. Simple memory: A theory for archicortex. Philos. Trans. Operating R.S. Gaines Roy. Soc. B. 252 (1971), 23-81. Systems Editor 12. Marr, D., and Poggio, T. Cooperative computation of stereo disparity. A.I. Memo 364, A.I. Lab., M.I.T., Cambridge, Mass., 1976. On-the-Fly Garbage 13. Minsky, M., and Papert, S. Perceptrons. M.I.T. Press, Cambridge, Mass., 1968. Collection: An Exercise in 14. Montanari, U. Networks of constraints: Fundamental properties and applications to picture processing. Inform. Sci. 7, 2(April 1974), Cooperation 95-132. 15. Rosenfeld, A., Hummel, R., and Zucker, S.W. Scene labelling by relaxation operations. IEEE Trans. Systems, Man, and Cybernetics Edsger W. Dijkstra SMC-6, 6(June 1976), 420-433. Burroughs Corporation 16. Sussman, G.J., and McDermott, D.V. From PLANNER to CONNIVER--a genetic approach. Proc. AFIPS 1972 FJCC, Vol. 41, AFIPS Press, Montvale, N.J., pp. 1171-1179. Leslie Lamport 17. Sussman, G.J., and Stallman, R.M. Forward reasoning and SRI International dependency-directed backtracking in a system for computer-aided circuit analysis. A.I. Memo 380, A.I. Lab., M.I.T., Cambridge, Mass., 1976. A.J. Martin, C.S. -

Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J
Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J. Keely. All Rights Reserved. Mathematical expressions can be typed online in a number of ways including plain text, ASCII codes, HTML tags, or using an equation editor (see Writing Mathematical Notation Online for overview). If the application in which you are working does not have an equation editor built in, then a common option is to write expressions horizontally in plain text. In doing so you have to format the expressions very carefully using appropriately placed parentheses and accurate notation. This document provides examples and important cautions for writing mathematical expressions in plain text. Section 1. How to Write Exponents Just as on a graphing calculator, when writing in plain text the caret key ^ (above the 6 on a qwerty keyboard) means that an exponent follows. For example x2 would be written as x^2. Example 1a. 4xy23 would be written as 4 x^2 y^3 or with the multiplication mark as 4*x^2*y^3. Example 1b. With more than one item in the exponent you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x2n must be written as x^(2n) and NOT as x^2n. Writing x^2n means xn2 . Example 1c. When using the quotient rule of exponents you often have to perform subtraction within an exponent. In such cases you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x5 The middle step of ==xx52− 3 must be written as x^(5-2) and NOT as x^5-2 which means x5 − 2 . -
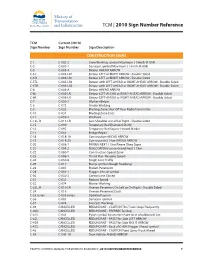
2010 Sign Number Reference for Traffic Control Manual
TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34 -
![Arxiv:1909.05204V3 [Cs.DC] 6 Feb 2020](https://docslib.b-cdn.net/cover/9182/arxiv-1909-05204v3-cs-dc-6-feb-2020-359182.webp)
Arxiv:1909.05204V3 [Cs.DC] 6 Feb 2020
Cogsworth: Byzantine View Synchronization Oded Naor, Technion and Calibra Mathieu Baudet, Calibra Dahlia Malkhi, Calibra Alexander Spiegelman, VMware Research Most methods for Byzantine fault tolerance (BFT) in the partial synchrony setting divide the local state of the nodes into views, and the transition from one view to the next dictates a leader change. In order to provide liveness, all honest nodes need to stay in the same view for a sufficiently long time. This requires view synchronization, a requisite of BFT that we extract and formally define here. Existing approaches for Byzantine view synchronization incur quadratic communication (in n, the number of parties). A cascade of O(n) view changes may thus result in O(n3) communication complexity. This paper presents a new Byzantine view synchronization algorithm named Cogsworth, that has optimistically linear communication complexity and constant latency. Faced with benign failures, Cogsworth has expected linear communication and constant latency. The result here serves as an important step towards reaching solutions that have overall quadratic communication, the known lower bound on Byzantine fault tolerant consensus. Cogsworth is particularly useful for a family of BFT protocols that already exhibit linear communication under various circumstances, but suffer quadratic overhead due to view synchro- nization. 1. INTRODUCTION Logical synchronization is a requisite for progress to be made in asynchronous state machine repli- cation (SMR). Previous Byzantine fault tolerant (BFT) synchronization mechanisms incur quadratic message complexities, frequently dominating over the linear cost of the consensus cores of BFT so- lutions. In this work, we define the view synchronization problem and provide the first solution in the Byzantine setting, whose latency is bounded and communication cost is linear, under a broad set of scenarios. -

Glossary of Linear Algebra Terms
INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w. -

Leading the Way in Scientific Computing. Addison-Wesley. I When Looking for the Best in Scientific Computing, You've Come to Rely on Addison-Wesley
Leading the way in scientific computing. Addison-Wesley. I When looking for the best in scientific computing, you've come to rely on Addison-Wesley. I Take a moment to see how we've made our list even stronger. The LATEX Companion sional programming languages. This book is the definitive user's Michael Goossens, Frank Mittelbach, and Alexander Samarin guide and reference manual for the CWEB system. This book is packed with information needed to use LATEX even 1994 (0-201 -57569-8) approx. 240 pp. Softcover more productively. It is a true companion to Leslie Lamport's users guide as well as a valuable complement to any LATEX introduction. Concrete Mathematics. Second Edition Describes the new LATEX standard. Ronald L. Graham, Donald E. Knuth, and Oren Patashnick 1994 (0-201 -54 199-8) 400 pp. Softcover With improvements to almost every page, the second edition of this classic text and reference introduces the mathematics that LATEX: A Document Preparation System, Second Edition supports advanced computer programming. Leslie Lamport 1994 (0-201 -55802-5) 672 pp. Hardcover The authoritative user's guide and reference manual has been revised to document features now available in the new standard Applied Mathematics@: Getting Started, Getting It Done software release-LATEX~E.The new edition features additional styles William T. Shaw and Jason Tigg and functions, improved font handling, and much more. This book shows how Mathematics@ can be used to solve problems in 1994 (0-201-52983-1) 256 pp. Softcover the applied sciences. Provides a wealth of practical tips and techniques. 1 994 (0-201 -542 1 7-X) 320 pp. -

Data Types & Arithmetic Expressions
Data Types & Arithmetic Expressions 1. Objective .............................................................. 2 2. Data Types ........................................................... 2 3. Integers ................................................................ 3 4. Real numbers ....................................................... 3 5. Characters and strings .......................................... 5 6. Basic Data Types Sizes: In Class ......................... 7 7. Constant Variables ............................................... 9 8. Questions/Practice ............................................. 11 9. Input Statement .................................................. 12 10. Arithmetic Expressions .................................... 16 11. Questions/Practice ........................................... 21 12. Shorthand operators ......................................... 22 13. Questions/Practice ........................................... 26 14. Type conversions ............................................. 28 Abdelghani Bellaachia, CSCI 1121 Page: 1 1. Objective To be able to list, describe, and use the C basic data types. To be able to create and use variables and constants. To be able to use simple input and output statements. Learn about type conversion. 2. Data Types A type defines by the following: o A set of values o A set of operations C offers three basic data types: o Integers defined with the keyword int o Characters defined with the keyword char o Real or floating point numbers defined with the keywords -

A Century of Mathematics in America, Peter Duren Et Ai., (Eds.), Vol
Garrett Birkhoff has had a lifelong connection with Harvard mathematics. He was an infant when his father, the famous mathematician G. D. Birkhoff, joined the Harvard faculty. He has had a long academic career at Harvard: A.B. in 1932, Society of Fellows in 1933-1936, and a faculty appointmentfrom 1936 until his retirement in 1981. His research has ranged widely through alge bra, lattice theory, hydrodynamics, differential equations, scientific computing, and history of mathematics. Among his many publications are books on lattice theory and hydrodynamics, and the pioneering textbook A Survey of Modern Algebra, written jointly with S. Mac Lane. He has served as president ofSIAM and is a member of the National Academy of Sciences. Mathematics at Harvard, 1836-1944 GARRETT BIRKHOFF O. OUTLINE As my contribution to the history of mathematics in America, I decided to write a connected account of mathematical activity at Harvard from 1836 (Harvard's bicentennial) to the present day. During that time, many mathe maticians at Harvard have tried to respond constructively to the challenges and opportunities confronting them in a rapidly changing world. This essay reviews what might be called the indigenous period, lasting through World War II, during which most members of the Harvard mathe matical faculty had also studied there. Indeed, as will be explained in §§ 1-3 below, mathematical activity at Harvard was dominated by Benjamin Peirce and his students in the first half of this period. Then, from 1890 until around 1920, while our country was becoming a great power economically, basic mathematical research of high quality, mostly in traditional areas of analysis and theoretical celestial mechanics, was carried on by several faculty members.