DOCSLIB.ORG

Math Symbol Tables

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Math Symbol Tables APPENDIX A I Math symbol tables A.I Hebrew letters Type: Print: Type: Print: \aleph ~ \beth :J \daleth l \gimel J All symbols but \aleph need the amssymb package. 346 Appendix A A.2 Greek characters Type: Print: Type: Print: Type: Print: \alpha a \beta f3 \gamma 'Y \digamma F \delta b \epsilon E \varepsilon E \zeta ( \eta 'f/ \theta () \vartheta {) \iota ~ \kappa ,.. \varkappa x \lambda ,\ \mu /-l \nu v \xi ~ \pi 7r \varpi tv \rho p \varrho (} \sigma (J \varsigma <; \tau T \upsilon v \phi ¢ \varphi 'P \chi X \psi 'ljJ \omega w \digamma and \ varkappa require the amssymb package. Type: Print: Type: Print: \Gamma r \varGamma r \Delta L\ \varDelta L.\ \Theta e \varTheta e \Lambda A \varLambda A \Xi ~ \varXi ~ \Pi II \varPi II \Sigma 2: \varSigma E \Upsilon T \varUpsilon Y \Phi <I> \varPhi t[> \Psi III \varPsi 1ft \Omega n \varOmega D All symbols whose name begins with var need the amsmath package. Math symbol tables 347 A.3 Y1EX binary relations Type: Print: Type: Print: \in E \ni \leq < \geq >'" \11 « \gg \prec \succ \preceq \succeq \sim \cong \simeq \approx \equiv \doteq \subset c \supset \subseteq c \supseteq \sqsubseteq c \sqsupseteq \smile \frown \perp 1- \models F \mid I \parallel II \vdash f- \dashv -1 \propto <X \asymp \bowtie [Xl \sqsubset \sqsupset \Join The latter three symbols need the latexsym package. 348 Appendix A A.4 AMS binary relations Type: Print: Type: Print: \leqs1ant :::::; \geqs1ant ): \eqs1ant1ess :< \eqs1antgtr :::> \lesssim < \gtrsim > '" '" < > \lessapprox ~ \gtrapprox \approxeq ~ \lessdot <:: \gtrdot Y \111 «< \ggg »> \lessgtr S \gtr1ess Z < >- \lesseqgtr > \gtreq1ess < > < \gtreqq1ess \lesseqqgtr > < ~ \doteqdot --;- \eqcirc = .2... '- \circeq - \fa11ingdotseq ---0 ~ A \risingdotseq ;- \triang1eq - \backsim '-" \thicksim '" \backsimeq '-"- \thickapprox ~ \preccur1yeq ~ \succcur1yeq ~ \cur1yeqprec =1:: \cur1yeqsucc ~ \precsim -< \succsim >- '" '" --< >- \precapprox ~ \succapprox ~ C :l \subseteqq - \supseteqq - \Subset IS \Supset 3! \vartriang1e1eft <l \vartriang1eright [> [> \triang1e1efteq <l- \triang1erighteq - \vDash 1= Wdash If- \Vvdash 1If- \sma11smile '--' \sma11frown r-. \shortmid I \shortpara11e1 II ~ \bumpeq ~ \Bumpeq ~ \between Q \pitchfork rh \varpropto ex \backepsilon ~ \b1acktriang1e1eft ... \b1acktriang1eright ~ \therefore . \because .. All symbols require the amssymb package. Math symbol tables 349 A.S AMS negated binary relations Type: Print: Type: Print: \ne =I- \notin rf- \nless 1- \ngtr f \nleq i \ngeq i \nleqslant 1, \ngeqslant 'I \nleqq ~ \ngeqq t \lneq :;; \gneq 2: \lneqq <7= \gneqq 7=> \lvertneqq ~ \gvertneqq >=1= \lnsim < ?- \gnsim ~ \lnapprox < r:j::, \gnapprox ~ \nprec -I< \nsucc ';f \npreceq ~ \nsucceq 'i \precneqq ~ \succneqq (:;; \precnsim -< ?- \succnsim ?->- \precnapprox -< >- ~ \succnapprox ~ \nsim "'" \ncong ~ \nshortmid { \nshortparallel 11 \nmid f \nparallel {t \nvdash J.L \nvDash ¥ \nVdash .w: \nVDash .l¥ \ntriangleleft 11 \ntriangleright ~ \ntrianglelefteq jl \ntrianglerighteq rt \nsubseteq ~ \nsupseteq 1J- \nsubseteqq ~ \nsupseteqq ;g \subsetneq ~ \supsetneq "2 \varsubsetneq ~ \varsupsetneq ;2 \subsetneqq C J 7= \supsetneqq 7= \varsubsetneqq ~ \varsupsetneqq ~ All symbols but \ne require the amssymb package. 350 Appendix A A.6 Binary operations Type: Print: Type: Print: \pm ± \mp =f \times x \cdot \circ 0 \bigcirc 0 \div \diamond <) \ast * \star * \cap n \cup U \sqcap n \sqcup U \wedge 1\ \vee V \triangleleft <J \triangleright I> \bigtriangleup /":, \bigtriangledown V \oplus EB \ominus e \otimes ® \oslash 0 \odot 8 \bullet • \dagger t \ddagger :j: \setminus \ \uplus I±I \wr I \amalg II \lhd <J \rhd (> (> \unlhd -<J \unrhd \dotplus + \centerdot \ltimes I>< \rtimes ~ \leftthreetimes A \rightthreetimes A \circleddash 8 \smallsetminus "- \barwedge /\ \doublebarwedge 1\ \curlywedge A \curlyvee y \veebar ":{ \intercal T \Cap Iii) \Cup l!!J \circledast ® \circledcirc @ \boxminus El \boxtimes ~ \boxdot c:J \boxplus B3 \divideontimes * I \And & This table is divided into four parts. The first part contains the binary operations in :£b.TEX. The second part requires the latexsym package. The third part contains the AMS additions; they require the amssymb package. The symbol \And requires the amsmath package. Math symbol tables 351 A.7 Arrows Type: Print: Type: Print: \leftarrow <- \rightarrow or \ to ---. \longleftarrow ~ \longrightarrow ---+ \Leftarrow ~ \Rightarrow :::} \Longleftarrow {== \Longrightarrow ==} \leftrightarrow f-+ \longleftrightarrow ~ \Leftrightarrow ¢:} \Longleftrightarrow ~ \uparrow i \downarrow 1 \Uparrow 11' \Downarrow JJ- \updownarrow 1 \Updownarrow ~ \nearrow / \searrow \swarrow ,/ \nwarrow "" \mapsto f-+ \longmapsto f-----+"" \hookleftarrow +--" \hookrightarrow ~ \leftharpoonup ~ \rightharpoonup ~ \leftharpoondown ~ \rightharpoondown ~ \rightleftharpoons ~ \leadsto "'* \leftleftarrows l= \rightrightarrows :4 \leftrightarrows =+ \rightleftarrows <= \Lleftarrow ~ \Rrightarrow ~ \twoheadleftarrow «--- \twoheadrightarrow -* \leftarrowtail r-< \rightarrowtail >---> \looparrowleft <--P \looparrowright '1-+ \upuparrows n \downdownarrows 11 \upharpoonleft 1 \upharpoonright r \downharpoonleft J \downharpoonright l \leftrightsquigarrow """" \rightsquigarrow """' \multimap -0 \nleftarrow +f- \nrightarrow -+> \nLeftarrow -#= \nRightarrow ~ \nleftrightarrow <++ \nLeftrightarrow {f;> This table is divided into three parts. The top part contains the symbols provided by Ib-TEX; the last command, \leadsto, requires the latexsym package. The middle table contains the AMS arrows; they all require the amssymb package. The bottom table lists the negated arrow symbols; they also require amssymb. 352 Appendix A A.8 Miscellaneous symbols Type: Print: Type: Print: \hbar Ii \ell C \imath z \jmath J \wp 8J \Re ~ \lm 'S \partial {) \infty 00 \prime I \emptyset 0 \backslash \ \forall 't/ \exists :3 \smallint J \triangle 6 \surd J \Vert II \top T \bot ..l \P ~ \8 § \dag t \ddag :j: \flat D \natural q \sharp ~ \angle L \clubsuit "- \diamondsuit <> \heartsuit 0 \spadesuit \neg -, • \Box 0 \Diamond <> \mho U \hslash Ii \complement C \backprime \ \vartriangle 6. \Bbbk Ik \varnothing 0 \diagup / \diagdown \blacktriangle A \blacktriangledown ""~ \triangledown \l \Game ~ \ square D \blacksquare \lozenge (; \blacklozenge • \measuredangle L \sphericalangle •<l: \circled8 ® \bigstar \Finv ..:J \eth *(3 \nexists ~ This table is divided into two parts. The top part contains the symbols provided by U\TEX; the last three commands require the latexsym package. The bottom table lists symbols from the AMS; they all require the amssymb package. Math symbol tables 353 A.9 Math spacing commands Short form: Full form: Size: Short form: Full form: \, \thinspace u \! \negthinspace \: \medspace u \negmedspace \; \thickspace u \negthickspace \quad LJ \qquad L--J The \medspace, \thickspace, \negmedspace, and \negthickspace commands require the amsmath package. A.iO Delimiters Name: Type: Print: Name: Type: Print: Left paren ( ( Right paren ) ) Left bracket [ [ Right bracket ] 1 Left brace \{ { Right brace \} } Reverse slash \backslash \ Forward slash / / Left angle \langle ( Right angle \rangle ) Vertical line 1 I Double vert. line \1 II Left floor \lfloor l Right floor \rfloor J Left ceiling \lceil I Right ceiling \rceil 1 Upper left corner \ulcorner r Upper right corner \urcorner I Lower left corner \llcorner L Lower right corner \lrcorner ...J The corners require the amsmath package. Name: Type: Print: Upward arrow \uparrow i Double upward arrow \Uparrow 1t' Downward arrow \downarrow ! Double downward arrow \Downarrow .lJ. Up-and-down arrow \updownarrow 1 Double up-and-down arrow \Updownarrow ~ 354 Appendix A A.ll Operators \arccos \arcsin \arctan \arg \cos \cosh \cot \coth \csc \dim \exp \hom \ker \lg \In \log \sec \sin \sinh \tan \tanh \varliminf \varlimsup \varinjlim \varprojlim The \var commands require the amsmath package. \det \gcd \inf \injlim \lim \liminf \limsup \max \min \projlim \Pr \sup The \injlim and \projlim commands require the amsmath package. Type: Inline Displayed Type: Inline Displayed n n \prod_{i=1Y{n} \coprod_{i=1}-{n} Un I1~=1 II i=1 II i=1 i=1 n n \bigcap_{i=1}-{n} \bigcup_{i=1}-{n} Un n~=1 n i=1 U i=1 i=1 n n \bigwedge_{i=1}-{n} \bigvee_{i=1}-{n} n 1\7=1 1\ V i=1 V i=1 i=l n n \bigsqcup_{i=1}-{n} U~=1 U \biguplus_{i=1}-{n} ltJ~=1 l±J i=1 i=1 n n \bigotimes_{i=1}-{n} Q9~1 ® \bigoplus_{i=1}-{n} EB~=1 EB i=1 i=1 n n \bigodot_{i=1}-{n} O~=1 0 \SUID_ {i=1Y{n} 2:~=1 L i=1 ;=1 Math symbol tables 355 A.12 Math accents \hat{a} a \Hat{a} a \widehat{a} a a\sphat a ~ \tilde{a} a \Tilde{a} a \widetilde{a} a a\sptilde a~ \acute{a} a \Acute{a} a \bar{a} a \Bar{a} a \breve{a} a \Breve{a} a a\spbreve aU \check{a} a \Check{a} a a\spcheck a V \dot{a} a \Dot{a} a a\spdot a' .. \ddot{a} ii \Ddot{a} a a\spddot a \dddot{a} a a\spdddot a ... \ddddot{a} a \grave{a} a \Grave{a} a \imath z \vec{a} a \Vec{a} a \jmath J The \dddot and \ddddot commands and all the capitalized commands require the amsmath package; the commands in the fourth column require the amsxtra package. A.13 Math font commands Type: Print: \mathbf{A} A \mathit{A} A \mathsf{A} A \mathrm{A} A \mathtt{A} A \mathnormal{A} A \mathbb{A} Pi,. \mathfrak{A} 2t \mathcal{A} A \boldsymbol{\alpha} Q The \mathbb, \mathfrak, and \mathcal commands require the amsfonts package. The \boldsymbol command requires the amsbsy package. APPENDIX B I Text symbol tables B.l Special text characters Type: Print: Type: Print: Type: Print: \# # \$ $ \% % - \& & \-n \- - , \-n \{ { \} } $1$ 1 @ @ $*$ * $\backslash$ \ Text symbol tables 357 B.2 Text accents
Load more

Recommended publications
  • Donald Knuth Fletcher Jones Professor of Computer Science, Emeritus Curriculum Vitae Available Online
    Donald Knuth Fletcher Jones Professor of Computer Science, Emeritus Curriculum Vitae available Online Bio BIO Donald Ervin Knuth is an American computer scientist, mathematician, and Professor Emeritus at Stanford University. He is the author of the multi-volume work The Art of Computer Programming and has been called the "father" of the analysis of algorithms. He contributed to the development of the rigorous analysis of the computational complexity of algorithms and systematized formal mathematical techniques for it. In the process he also popularized the asymptotic notation. In addition to fundamental contributions in several branches of theoretical computer science, Knuth is the creator of the TeX computer typesetting system, the related METAFONT font definition language and rendering system, and the Computer Modern family of typefaces. As a writer and scholar,[4] Knuth created the WEB and CWEB computer programming systems designed to encourage and facilitate literate programming, and designed the MIX/MMIX instruction set architectures. As a member of the academic and scientific community, Knuth is strongly opposed to the policy of granting software patents. He has expressed his disagreement directly to the patent offices of the United States and Europe. (via Wikipedia) ACADEMIC APPOINTMENTS • Professor Emeritus, Computer Science HONORS AND AWARDS • Grace Murray Hopper Award, ACM (1971) • Member, American Academy of Arts and Sciences (1973) • Turing Award, ACM (1974) • Lester R Ford Award, Mathematical Association of America (1975) • Member, National Academy of Sciences (1975) 5 OF 44 PROFESSIONAL EDUCATION • PhD, California Institute of Technology , Mathematics (1963) PATENTS • Donald Knuth, Stephen N Schiller. "United States Patent 5,305,118 Methods of controlling dot size in digital half toning with multi-cell threshold arrays", Adobe Systems, Apr 19, 1994 • Donald Knuth, LeRoy R Guck, Lawrence G Hanson.
    [Show full text]
  • Typeset MMIX Programs with TEX Udo Wermuth Abstract a TEX Macro
    TUGboat, Volume 35 (2014), No. 3 297 Typeset MMIX programs with TEX Example: In section 9 the lines \See also sec- tion 10." and \This code is used in section 24." are given. Udo Wermuth No such line appears in section 10 as it only ex- tends the replacement code of section 9. (Note that Abstract section 10 has in its headline the number 9.) In section 24 the reference to section 9 stands for all of ATEX macro package is presented as a literate pro- the eight code lines stated in sections 9 and 10. gram. It can be included in programs written in the If a section is not used in any other section then languages MMIX or MMIXAL without affecting the it is a root and during the extraction of the code a assembler. Such an instrumented file can be pro- file is created that has the name of the root. This file cessed by TEX to get nicely formatted output. Only collects all the code in the sequence of the referenced a new first line and a new last line must be entered. sections from the code part. The collection process And for each end-of-line comment a flag is set to for all root sections is called tangle. A second pro- indicate that the comment is written in TEX. cess is called weave. It outputs the documentation and the code parts as a TEX document. How to read the following program Example: The following program has only one The text that starts in the next chapter is a literate root that is defined in section 4 with the headline program [2, 1] written in a style similar to noweb [7].
    [Show full text]
  • The Nth Root of a Number Page 1
    Lecture Notes The nth Root of a Number page 1 Caution! Currently, square roots are dened differently in different textbooks. In conversations about mathematics, approach the concept with caution and rst make sure that everyone in the conversation uses the same denition of square roots. Denition: Let A be a non-negative number. Then the square root of A (notation: pA) is the non-negative number that, if squared, the result is A. If A is negative, then pA is undened. For example, consider p25. The square-root of 25 is a number, that, when we square, the result is 25. There are two such numbers, 5 and 5. The square root is dened to be the non-negative such number, and so p25 is 5. On the other hand, p 25 is undened, because there is no real number whose square, is negative. Example 1. Evaluate each of the given numerical expressions. a) p49 b) p49 c) p 49 d) p 49 Solution: a) p49 = 7 c) p 49 = unde ned b) p49 = 1 p49 = 1 7 = 7 d) p 49 = 1 p 49 = unde ned Square roots, when stretched over entire expressions, also function as grouping symbols. Example 2. Evaluate each of the following expressions. a) p25 p16 b) p25 16 c) p144 + 25 d) p144 + p25 Solution: a) p25 p16 = 5 4 = 1 c) p144 + 25 = p169 = 13 b) p25 16 = p9 = 3 d) p144 + p25 = 12 + 5 = 17 . Denition: Let A be any real number. Then the third root of A (notation: p3 A) is the number that, if raised to the third power, the result is A.
    [Show full text]
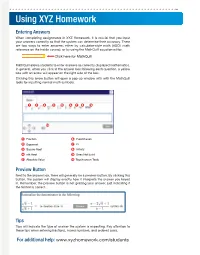
  • Using XYZ Homework
    Using XYZ Homework Entering Answers When completing assignments in XYZ Homework, it is crucial that you input your answers correctly so that the system can determine their accuracy. There are two ways to enter answers, either by calculator-style math (ASCII math reference on the inside covers), or by using the MathQuill equation editor. Click here for MathQuill MathQuill allows students to enter answers as correctly displayed mathematics. In general, when you click in the answer box following each question, a yellow box with an arrow will appear on the right side of the box. Clicking this arrow button will open a pop-up window with with the MathQuill tools for inputting normal math symbols. 1 2 3 4 5 6 7 8 9 10 1 Fraction 6 Parentheses 2 Exponent 7 Pi 3 Square Root 8 Infinity 4 nth Root 9 Does Not Exist 5 Absolute Value 10 Touchscreen Tools Preview Button Next to the answer box, there will generally be a preview button. By clicking this button, the system will display exactly how it interprets the answer you keyed in. Remember, the preview button is not grading your answer, just indicating if the format is correct. Tips Tips will indicate the type of answer the system is expecting. Pay attention to these tips when entering fractions, mixed numbers, and ordered pairs. For additional help: www.xyzhomework.com/students ASCII Math (Calculator Style) Entry Some question types require a mathematical expression or equation in the answer box. Because XYZ Homework follows order of operations, the use of proper grouping symbols is necessary.
    [Show full text]
  • Just-In-Time 22-25 Notes
    Just-In-Time 22-25 Notes Sections 22-25 1 JIT 22: Simplify Radical Expressions Definition of nth Roots p • If n is a natural number and yn = x, then n x = y. p • n x is read as \the nth root of x". p { 3 8 = 2 because 23 = 8. p { 4 81 = 3 because 34 = 81. p 2 • When n =p 2 we call it a \square root". However, instead of writing x, we drop the 2 and just write x. So, for example: p { 16 = 4 because 42 = 16. Domain of Radical Expressions • Howp do you find the even root of a negative number? For example, imagine the answer to 4 −16 is the number x. This means x4 = −16. The problem is, if we raise a number to the fourth power, we never get a negative answer: (2)4 = 2 · 2 · 2 · 2 = 16 (−2)4 = (−2)(−2)(−2)(−2) = 16 • Since there is no solution here for x, we say that the fourth root is undefined for negative numbers. • However, the same idea applies to any even root (square roots, fourth roots, sixth roots, etc) p If the expression contains n B where n is even, then B ≥ 0 . Properties of Roots/Radicals p • n xn = x if n is odd. p • n xn = jxj if n is even. p p p • n xy = n x n y (When n is even, x and y need to be nonnegative.) p q n x n x p • y = n y (When n is even, x and y need to be nonnegative.) p p m • n xm = ( n x) (When n is even, x needs to be nonnegative.) mp p p • n x = mn x 1 Examples p p 1.
    [Show full text]
  • Proving the Existence of the Nth Root by Induction
    Proving the existence of the nth root by induction. Alvaro Salas∗ Abstract In this paper we prove by induction on n that any positive real number has nth root. Key words and phrases: nth root, supremum, least upper bound axiom. 1 Auxiliary facts We define the set R of real numbers as a numeric ordered field in which the following axiom holds: Least Upper Bound Axiom : If = E R is a non empty set bounded from above, then there ∅ 6 ⊆ exists a least upper bound for E. The least upper bound of E is unique and it is denoted by sup E. If x = sup E, then : A. t x for any t E, that is, x is an upper bound for E. ≤ ∈ B. For any δ > 0 we may find t E such that x δ < t x. ∈ − ≤ Definition 1.1 Let n be a positive integer and a> 0. We say that x is a nth root of a if xn = a. It is easy to show that if a has an nth root, then this root is unique. This follows from the fact that if x and y are positive numbers for which xn = yn, then x = y. The nth root of a is denoted by √n a. Lemma 1.1 Suppose that a> 0 and n is a positive integer. The set n arXiv:0805.3303v1 [math.GM] 21 May 2008 E = t 0 t < a . { ≥ | } is not empty and bounded from above. Proof. E is not empty, because 0 E. On the other hand, it is easy to show by induction on n ∈ that (a + 1)n > a.
    [Show full text]
  • Implementation of a MIX Emulator: a Case Study of the Scala Programming Language Facilities
    ISSN 2255-8691 (online) Applied Computer Systems ISSN 2255-8683 (print) December 2017, vol. 22, pp. 47–53 doi: 10.1515/acss-2017-0017 https://www.degruyter.com/view/j/acss Implementation of a MIX Emulator: A Case Study of the Scala Programming Language Facilities Ruslan Batdalov1, Oksana Ņikiforova2 1, 2 Riga Technical University, Latvia Abstract – Implementation of an emulator of MIX, a mythical synchronous manner, possible errors in a program may remain computer invented by Donald Knuth, is used as a case study of unnoticed. In the authors’ opinion, these checks are useful in the features of the Scala programming language. The developed mastering how to write correct programs because similar emulator provides rich opportunities for program debugging, such as tracking intermediate steps of program execution, an errors often occur in a modern program despite all changes in opportunity to run a program in the binary or the decimal mode hardware and software technologies. Therefore, it would be of MIX, verification of correct synchronisation of input/output helpful if an emulator supported running programs in different operations. Such Scala features as cross-compilation, family modes and allowed checking that the execution result was the polymorphism and support for immutable data structures have same in all cases. proved to be useful for implementation of the emulator. The The programming language chosen by the authors for the authors of the paper also propose some improvements to these features: flexible definition of family-polymorphic types, implementation of an emulator supporting these features is integration of family polymorphism with generics, establishing Scala. This choice is arbitrary to some extent and rather full equivalence between mutating operations on mutable data dictated by the authors’ interest in the features of this types and copy-and-modify operations on immutable data types.
    [Show full text]
  • Powers of Complex Numbers in Polar Form (2+I)2 =
    Powers of Complex Numbers in Polar Form (2+i)2 = (2+i)12 = Powers of Complex Numbers in Polar Form Let z = r(cosθ +isinθ) z2 = r(cosθ +isinθ)r(cosθ +isinθ) = r2(cos2θ +isin2θ) z3 = r2(cos2θ +isin2θ)r(cosθ +isinθ) = r3(cos3θ +isin3θ) z4 = r3(cos3θ +isin3θ)r(cosθ +isinθ) = r4(cos4θ +isin4θ) The formula for the nth power of a complex number in polar form is known as DeMoivre's Theorem (in honor of the French mathematician Abraham DeMoivre (1667‐1754). DeMoivre's Theorem Let z = r(cosθ+isinθ) be a complex number in polar form. If n is a positive integer, z to the nth power, zn, is zn = [r(cosθ+isinθ)]n = rn[cos(nθ)+isin(nθ)] = rnCiS(nθ) Ex1. Try. Ex2. Try. Roots of a Complex Number in Polar Form Yesterday we saw that [2(cos20o +isin20o)]6 = 64(cos120o + isin120o) Thinking backwards we could note that: A sixth root of 64(cos120o + isin120o) is 2(cos20o +isin20o) It is one of SIX distinct 6th roots of 64cis120o. Nth Root of a Complex Number In general, if a complex number, z, satisfies the equation zn = w, then we can say that z is a complex nth root of w. Also, z is one of n complex nth roots of w. Given the fact that roots are actually powers (remember x1/2 = √x), DeMoivre's Theorem can also be applied to roots... DeMoivre's Theorem for Finding Complex Roots Let w = rcisθ be a complex number in polar form. If w ≠ 0, then w has n distinct complex nth roots given by the formula: (radians) or (degrees) where k = 0, 1, 2, ..., n‐1.
    [Show full text]
  • Complex Numbers and Polar Coordinates Complex Numbers
    CHAPTER 8 Complex Numbers and Polar Coordinates Copyright © Cengage Learning. All rights reserved. SECTION 8.4 Roots of a Complex Number Copyright © Cengage Learning. All rights reserved. Learning Objectives 1 Find both square roots of a complex number. 2 Find all nth roots of a complex number. 3 Graph the nth roots of a complex number. 4 Use roots to solve an equation. 3 Roots of a Complex Number Every real (or complex) number has exactly two square roots, three cube roots, and four fourth roots. In fact, every real (or complex) number has exactly n distinct nth roots, a surprising and attractive fact about numbers. The key to finding these roots is trigonometric form for complex numbers. 4 Roots of a Complex Number Suppose that z and w are complex numbers such that w is an nth root of z. That is, 5 Example 1 Find the four fourth roots of . Solution: According to the formula given in our theorem on roots, the four fourth roots will be 6 Example 1 – Solution cont’d Replacing k with 0, 1, 2, and 3, we have 7 Example 1 – Solution cont’d It is interesting to note the graphical relationship among these four roots, as illustrated in Figure 1. Figure 1 8 Example 1 – Solution cont’d Because the modulus for each root is 2, the terminal point of the vector used to represent each root lies on a circle of radius 2. The vector representing the first root makes an angle of /n = 15° with the positive x-axis, then each following root has a vector that is rotated an additional 360°/n = 90° in the counterclockwise direction from the previous root.
    [Show full text]
  • Literate Programming and Reproducible Research
    JSS Journal of Statistical Software January 2012, Volume 46, Issue 3. http://www.jstatsoft.org/ A Multi-Language Computing Environment for Literate Programming and Reproducible Research Eric Schulte Dan Davison University of New Mexico Counsyl Thomas Dye Carsten Dominik University of Hawai`i University of Amsterdam Abstract We present a new computing environment for authoring mixed natural and com- puter language documents. In this environment a single hierarchically-organized plain text source file may contain a variety of elements such as code in arbitrary program- ming languages, raw data, links to external resources, project management data, working notes, and text for publication. Code fragments may be executed in situ with graphical, numerical and textual output captured or linked in the file. Export to LATEX, HTML, LATEX beamer, DocBook and other formats permits working reports, presentations and manuscripts for publication to be generated from the file. In addition, functioning pure code files can be automatically extracted from the file. This environment is implemented as an extension to the Emacs text editor and provides a rich set of features for authoring both prose and code, as well as sophisticated project management capabilities. Keywords: literate programming, reproducible research, compendium, WEB, Emacs. 1. Introduction There are a variety of settings in which it is desirable to mix prose, code, data, and compu- tational results in a single document. Scientific research increasingly involves the use of computational tools.
    [Show full text]
  • Analysis of the Relationship Between the Nth Root Which Is a Whole Number and the N Consecutive Odd Numbers
    http://jct.sciedupress.com Journal of Curriculum and Teaching Vol. 4, No. 2; 2015 Analysis of the Relationship between the nth Root which is a Whole Number and the n Consecutive Odd Numbers Kwenge Erasmus1,*, Mwewa Peter2 & Mulenga H.M3 1Mpika Day Secondary School, P.O. Box 450004, Mpika, Zambia 2Department of Mathematics and Statistics, Mukuba University, P.O. Box 20382, Itimpi, Kitwe, Zambia 3Department of Mathematics, Copperbelt University, P.O. Box 21692, Kitwe, Zambia *Correspondence: Mpika Day Secondary School, P.O. Box 450004, Mpika, Zambia. Tel: 260-976-379-410. E-mail: [email protected] Received: April 22, 2015 Accepted: July 12, 2015 Online Published: August 7, 2015 doi:10.5430/jct.v4n2p35 URL: http://dx.doi.org/10.5430/jct.v4n2p35 Abstract The study was undertaken to establish the relationship between the roots of the perfect numbers and the n consecutive odd numbers. Odd numbers were arranged in such a way that their sums were either equal to the perfect square number or equal to a cube. The findings on the patterns and relationships of the numbers showed that there was a relationship between the roots of numbers and n consecutive odd numbers. From these relationships a general formula was derived which can be used to determine the number of consecutive odd numbers that can add up to get the given number and this relationship was used to define the other meaning of nth root of a given perfect number from consecutive n odd numbers point of view. If the square root of 4 is 2, then it means that there are 2 consecutive odd numbers that can add up to 4, if the cube root of 27 is 3, then there are 3 consecutive odd number that add up to 27, if the fifth root of 32 is 5, then it means that there are 5 consecutive odd numbers that add up to 32.
    [Show full text]
  • Analytic Solutions to Algebraic Equations
    Analytic Solutions to Algebraic Equations Mathematics Tomas Johansson LiTH{MAT{Ex{98{13 Supervisor: Bengt Ove Turesson Examiner: Bengt Ove Turesson LinkÄoping 1998-06-12 CONTENTS 1 Contents 1 Introduction 3 2 Quadratic, cubic, and quartic equations 5 2.1 History . 5 2.2 Solving third and fourth degree equations . 6 2.3 Tschirnhaus transformations . 9 3 Solvability of algebraic equations 13 3.1 History of the quintic . 13 3.2 Galois theory . 16 3.3 Solvable groups . 20 3.4 Solvability by radicals . 22 4 Elliptic functions 25 4.1 General theory . 25 4.2 The Weierstrass } function . 29 4.3 Solving the quintic . 32 4.4 Theta functions . 35 4.5 History of elliptic functions . 37 5 Hermite's and Gordan's solutions to the quintic 39 5.1 Hermite's solution to the quintic . 39 5.2 Gordan's solutions to the quintic . 40 6 Kiepert's algorithm for the quintic 43 6.1 An algorithm for solving the quintic . 43 6.2 Commentary about Kiepert's algorithm . 49 7 Conclusion 51 7.1 Conclusion . 51 A Groups 53 B Permutation groups 54 C Rings 54 D Polynomials 55 References 57 2 CONTENTS 3 1 Introduction In this report, we study how one solves general polynomial equations using only the coef- ¯cients of the polynomial. Almost everyone who has taken some course in algebra knows that Galois proved that it is impossible to solve algebraic equations of degree ¯ve or higher, using only radicals. What is not so generally known is that it is possible to solve such equa- tions in another way, namely using techniques from the theory of elliptic functions.
    [Show full text]