DOCSLIB.ORG

Analytic Solutions to Algebraic Equations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Analytic Solutions to Algebraic Equations Mathematics Tomas Johansson LiTH{MAT{Ex{98{13 Supervisor: Bengt Ove Turesson Examiner: Bengt Ove Turesson LinkÄoping 1998-06-12 CONTENTS 1 Contents 1 Introduction 3 2 Quadratic, cubic, and quartic equations 5 2.1 History . 5 2.2 Solving third and fourth degree equations . 6 2.3 Tschirnhaus transformations . 9 3 Solvability of algebraic equations 13 3.1 History of the quintic . 13 3.2 Galois theory . 16 3.3 Solvable groups . 20 3.4 Solvability by radicals . 22 4 Elliptic functions 25 4.1 General theory . 25 4.2 The Weierstrass } function . 29 4.3 Solving the quintic . 32 4.4 Theta functions . 35 4.5 History of elliptic functions . 37 5 Hermite's and Gordan's solutions to the quintic 39 5.1 Hermite's solution to the quintic . 39 5.2 Gordan's solutions to the quintic . 40 6 Kiepert's algorithm for the quintic 43 6.1 An algorithm for solving the quintic . 43 6.2 Commentary about Kiepert's algorithm . 49 7 Conclusion 51 7.1 Conclusion . 51 A Groups 53 B Permutation groups 54 C Rings 54 D Polynomials 55 References 57 2 CONTENTS 3 1 Introduction In this report, we study how one solves general polynomial equations using only the coef- ¯cients of the polynomial. Almost everyone who has taken some course in algebra knows that Galois proved that it is impossible to solve algebraic equations of degree ¯ve or higher, using only radicals. What is not so generally known is that it is possible to solve such equa- tions in another way, namely using techniques from the theory of elliptic functions. Galois theory and the theory of elliptic functions are both extensive and deep. But to understand and ¯nd a way of solving polynomial equations we do not need all this theory. The aim here is to pick out only the part of the theory which is necessary to understand why not all equations are solvable by radicals, and the alternative procedures by which we solve them. We will concentrate on ¯nding an algorithm for the quintic equation. In Chapter 2 we examine the history of polynomial equations. We also present the formulas for solutions to equations of degree less then ¯ve. A basic tool, the Tschirnhaus transformation, is introduced. These transformations are used to simplify the solution process by transforming a polynomial into another where some coe±cients are zero. In Chapter 3 we introduce some Galois theory. In Galois theory one examines the rela- tionship between the permutation group of the roots and a ¯eld containing the coe±cients of the polynomial. Here we present only as much theory as is necessary to understand why not all polynomial equations are solvable by radicals. The history of the quintic equation is also presented. In Chapter 4 we introduce the elliptic functions and examine their basic properties. We concentrate on one speci¯c elliptic function, namely the Weierstrass } function. We show that with the help of this function one can solve the quintic equation. However, this is just a theoretical possibility. To be able to get a practical algorithm, we need to know some facts about theta functions, with which we also deal in this chapter. The history of elliptic functions is included at the end of this chapter. Here we also present the general formula for solving any polynomial equation due to H. Umemura. This formula is also only of theoretical value, so we will look at other ways of solving the quintic. We present three such methods in the last chapter. The one that we will concentrate on is Kiepert's, because it uses both elliptic functions and Tschirnhaus transformations in a clear and straightforward way. In Chapter 5 we present two algorithms for solving the quintic, which are due to Hermite and Gordan. Hermite uses a more analytic method compared with Gordan's solution, which involves the use of the icosahedron. In Chapter 6 we present Kiepert's algorithm for the quintic. This lends itself to imple- mentation on a computer. This has in fact been done by B. King and R. Can¯eld, and at the end of the chapter we discuss their results. We conclude with an Appendix. Here one can ¯nd the most basic facts about groups, rings, and polynomials. Acknowledgment I would like to thank the following people: my supervisor Bengt Ove Turesson for helping me with this report and for teaching me LATEX 2" in which this report is written, Peter Hackman for helpfull hints about Galois theory, and Gunnar Fogelberg for historical background. I also thank Thomas Karlsson who told me that this examination work was available, and Bruce King for telling me about his work on the quintic. I also express my gratitude to John H. Conway, Keith Dennis, and William C. Waterhouse for giving me information about L. Kiepert. 4 1 INTRODUCTION 5 2 Quadratic, cubic, and quartic equations In this chapter we shall take a brief look at the history of equations of degree less than ¯ve. We will also study the techniques for solving these equations. One such technique, the Tschirnhaus transformation, will be examined in Section 2.3. 2.1 History Polynomial equations arise quite naturally in mathematics, when dealing with basic math- ematical problems, and so their study has a long history. The attempts to solve certain of these equations have lead to new and exciting theories in mathematics, with the result that polynomial equations has been an important cornerstone in the development to modern mathematics. It is known that in ancient Babylonia (2000 { 600 B.C.), one was able to solve the second order equation x2 + c x + c = 0; c R; 1 0 i 2 using the famous formula 2 c1 c1 x = c0: ¡ 2 § r 4 ¡ They could, of course, not deal with all of the roots, since they did not have access to the complex numbers. Archaeologists have found tablets with cuneiform signs, where problems concerning second order equations are dealt with. Starting with geometric problems, they were led to these equations by the Pythagorean theorem. The Babylonians also studied some special equations of third degree. The Greeks (600 B.C. { 300 A.D.) had a more geometric viewpoint of mathematics compared to the Babylonians, but they also considered second order equations. They made geometric solutions to the quadratic and constructed the segment x from known segments c0 and c1. Problems like trisecting an angle and doubling the volume of the cube led the Greeks to third degree equations which they tried to solve; but they had no general method to for solving such equations. The Hindus (600 B.C. { 1000 A.D.) invented the number zero, negative numbers, and the position system. Brahmagupta dealt with quadratic equations. The solutions were more algebraic than those of the Babylonians. The Arabs (500 B.C. { 1000 A.D.) enjoyed algebra. The famous al-Khwarizmi dealt with algebra in his book Al-jabr wa'l muqabala around 800 A.D. In this book, he exam- ined certain types of second order equations (and none of higher degree). Another Arab mathematician, Omar Khayyam (1048{1131) classi¯ed third degree equations and exam- ined their roots in some special cases. He also investigated equations of fourth degree. Fore more details about mathematics in these old cultures, see Boyer [2] and van der Waer- den [25]. Europe began to participate in the development of mathematics soon after the Arabs. The Italian Leonardo Fibonacci (1170{1250) wrote Liber Abacci, where he tried to solve quadratic equations in one or more variables. In Europe in the Middle Ages, competitions in mathematics were popular. This en- couraged the development of the art of solving equations. A new era began around the 6 2 QUADRATIC, CUBIC, AND QUARTIC EQUATIONS beginning of the ¯fteenth centuary in Italy, when Scipione del Ferro (1465{1526) succeeded in solving the equation 3 x + c1x + c0 = 0: In Section 2.3, we will show that every third degree equation can be transformed to the above form, which means that del Ferro had solved the general cubic equation. Before his death, del Ferro told his student Fior of his method for solving cubics. Fior challenged another Italian, Niccolo Tartaglia (1500{1557), to a mathematical duel. This forced Tartaglia, who knew that Fior could solve such equations, to ¯nd a general method for solving the cubic. Tartaglia succeded with this and thus won the competition. Tartaglia told Girolamo Cardano (1501{1576) about his method. Cardano published the method in his book Ars Magna (around 1540). Here he observed that, in certain cases, the method yields roots of negative numbers, and that these could be real numbers. This means that he was touching upon the complex numbers. Cardano made his student Lodovico Ferrari (1522{1565) solve the fourth degree equation, i.e., the quartic. Ferrari succeeded with this, and Cardano also published this method in Ars Magna. The case when Cardanos formulas lead to roots of negative numbers was studied by Rafael Bombelli (1526{1573) in his book Algebra in 1560. After the Italians, many famous mathematicians examined these equations, for example Francois Vi`ete (1540{1603) and Ehrenfried Walter von Tschirnhaus (1651{1708). It was ¯nally the German mathematician Gottfried von Leibniz (1646{1716) who, with- out any geometry, veri¯ed these formulas. More information about these Italians and the solutions to third and fourth degree equations can be found in Stillwell [24]. 2.2 Solving third and fourth degree equations Below we shall present the formulas for the solution of cubic and quartic equations.
Recommended publications
  • Arxiv:1406.1948V2 [Math.GM] 18 Dec 2014 Hr = ∆ Where H Ouino 1 Is (1) of Solution the 1

    Arxiv:1406.1948V2 [Math.GM] 18 Dec 2014 Hr = ∆ Where H Ouino 1 Is (1) of Solution the 1

    Solution of Polynomial Equations with Nested Radicals Nikos Bagis Stenimahou 5 Edessa Pellas 58200, Greece [email protected] Abstract In this article we present solutions of arbitrary polynomial equations in nested periodic radicals Keywords: Nested Radicals; Quintic; Sextic; Septic; Equations; Polynomi- als; Solutions; Higher functions; 1 A general type of equations Consider the following general type of equations ax2µ + bxµ + c = xν . (1) Then (1) can be written in the form b 2 ∆2 a xµ + = xν , (2) 2a − 4a where ∆ = √b2 4ac. Hence − 2 µ b ∆ 1 ν x = − + 2 + x (3) 2a r4a a Set now √d x = x1/d, d Q 0 , then ∈ + −{ } 2 µ b ∆ 1 x = − + + xν (4) s 2a 4a2 a arXiv:1406.1948v2 [math.GM] 18 Dec 2014 r hence µ/ν 2 ν b ∆ 1 ν x = − + 2 + x (5) s 2a r4a a Theorem 1. The solution of (1) is µ v 2 µ/ν 2 2 u b v ∆ 1 b ∆ 1 µ/ν b ∆ x = u− + u + v− + v + − + + ... (6) u 2a u4a2 a u 2a u4a2 a s 2a 4a2 u u u u r u u u t t t t 1 Proof. Use relation (4) and repeat it infinite times. Corollary 1. The equation ax6 + bx5 + cx4 + dx3 + ex2 + fx + g = 0 (7) is always solvable with nested radicals. Proof. We know (see [1]) that all sextic equations, of the most general form (7) are equivalent by means of a Tchirnhausen transform y = kx4 + lx3 + mx2 + nx + s (8) to the form 6 2 y + e1y + f1y + g1 = 0 (9) But the last equation is of the form (1) with µ = 1 and ν = 6 and have solution 2 1/6 2 2 f v ∆ 1 f ∆ 1 1/6 f ∆ y = 1 + u 1 v 1 + 1 1 + 1 + ..
  • ALGEBRAIC GEOMETRY (1) Compute the Points of Intersection

    ALGEBRAIC GEOMETRY (1) Compute the Points of Intersection

    ALGEBRAIC GEOMETRY HOMEWORK 5 (1) Compute the points of intersection of the circle x2 +y2 +x−y = 0 with the lemniscate (x2 +y2)2 = x2 −y2 using resultants (can you compute the affine points of intersections directly?), and compute the multiplicities. Explain which coordinate system you choose, how the equations look like, what the resultant is, and what its factors are. (2) Here you will learn how to solve cubics using resultants. Assume you want to solve the cubic equation x3 + ax2 + bx + c = 0. (a) Show that the substitution y = x + a/3 transforms the cubic into y3 + By + C = 0. (b) Now assume that we have to solve x3 + bx + c = 0. Using linear re- lations y = rx ∗ b will not make the linear term disappear (without bringing back the quadratic term). Thus we try to put y = x2 + cx + d and then eliminate x using resultants: type in p = polresultant(x^3+b*x+c,y-x^2-d*x-e,x) polcoeff(p,2,y) polcoeff(p,1,y) (you can find out what polcoeff is doing by typing ?polcoeff). Now we know that we can keep the quadratic term out of the equation by choosing e = 2b/3. With this value of e go back and recompute the resultant; this will now be a cubic in y without quadratic term. The coefficient of the linear term can be made to disappear by solving a quadratic equation (which is called the resolvent of the original cubic). (c) Thus you can solve the cubic by solving the resolvent, using the trans- formations above to turn the cubic into a pure cubic y3 + c, which in turn is easy to solve.
  • Algorithmic Factorization of Polynomials Over Number Fields

    Algorithmic Factorization of Polynomials Over Number Fields

    Rose-Hulman Institute of Technology Rose-Hulman Scholar Mathematical Sciences Technical Reports (MSTR) Mathematics 5-18-2017 Algorithmic Factorization of Polynomials over Number Fields Christian Schulz Rose-Hulman Institute of Technology Follow this and additional works at: https://scholar.rose-hulman.edu/math_mstr Part of the Number Theory Commons, and the Theory and Algorithms Commons Recommended Citation Schulz, Christian, "Algorithmic Factorization of Polynomials over Number Fields" (2017). Mathematical Sciences Technical Reports (MSTR). 163. https://scholar.rose-hulman.edu/math_mstr/163 This Dissertation is brought to you for free and open access by the Mathematics at Rose-Hulman Scholar. It has been accepted for inclusion in Mathematical Sciences Technical Reports (MSTR) by an authorized administrator of Rose-Hulman Scholar. For more information, please contact [email protected]. Algorithmic Factorization of Polynomials over Number Fields Christian Schulz May 18, 2017 Abstract The problem of exact polynomial factorization, in other words expressing a poly- nomial as a product of irreducible polynomials over some field, has applications in algebraic number theory. Although some algorithms for factorization over algebraic number fields are known, few are taught such general algorithms, as their use is mainly as part of the code of various computer algebra systems. This thesis provides a summary of one such algorithm, which the author has also fully implemented at https://github.com/Whirligig231/number-field-factorization, along with an analysis of the runtime of this algorithm. Let k be the product of the degrees of the adjoined elements used to form the algebraic number field in question, let s be the sum of the squares of these degrees, and let d be the degree of the polynomial to be factored; then the runtime of this algorithm is found to be O(d4sk2 + 2dd3).
  • Some Properties of the Discriminant Matrices of a Linear Associative Algebra*

    Some Properties of the Discriminant Matrices of a Linear Associative Algebra*

    570 R. F. RINEHART [August, SOME PROPERTIES OF THE DISCRIMINANT MATRICES OF A LINEAR ASSOCIATIVE ALGEBRA* BY R. F. RINEHART 1. Introduction. Let A be a linear associative algebra over an algebraic field. Let d, e2, • • • , en be a basis for A and let £»•/*., (hjik = l,2, • • • , n), be the constants of multiplication corre­ sponding to this basis. The first and second discriminant mat­ rices of A, relative to this basis, are defined by Ti(A) = \\h(eres[ CrsiCij i, j=l T2(A) = \\h{eres / ,J CrsiC j II i,j=l where ti(eres) and fa{erea) are the first and second traces, respec­ tively, of eres. The first forms in terms of the constants of multi­ plication arise from the isomorphism between the first and sec­ ond matrices of the elements of A and the elements themselves. The second forms result from direct calculation of the traces of R(er)R(es) and S(er)S(es), R{ei) and S(ei) denoting, respectively, the first and second matrices of ei. The last forms of the dis­ criminant matrices show that each is symmetric. E. Noetherf and C. C. MacDuffeeJ discovered some of the interesting properties of these matrices, and shed new light on the particular case of the discriminant matrix of an algebraic equation. It is the purpose of this paper to develop additional properties of these matrices, and to interpret them in some fa­ miliar instances. Let A be subjected to a transformation of basis, of matrix M, 7 J rH%j€j 1,2, *0).
  • The Nth Root of a Number Page 1

    The Nth Root of a Number Page 1

    Lecture Notes The nth Root of a Number page 1 Caution! Currently, square roots are dened differently in different textbooks. In conversations about mathematics, approach the concept with caution and rst make sure that everyone in the conversation uses the same denition of square roots. Denition: Let A be a non-negative number. Then the square root of A (notation: pA) is the non-negative number that, if squared, the result is A. If A is negative, then pA is undened. For example, consider p25. The square-root of 25 is a number, that, when we square, the result is 25. There are two such numbers, 5 and 5. The square root is dened to be the non-negative such number, and so p25 is 5. On the other hand, p 25 is undened, because there is no real number whose square, is negative. Example 1. Evaluate each of the given numerical expressions. a) p49 b) p49 c) p 49 d) p 49 Solution: a) p49 = 7 c) p 49 = unde ned b) p49 = 1 p49 = 1 7 = 7 d) p 49 = 1 p 49 = unde ned Square roots, when stretched over entire expressions, also function as grouping symbols. Example 2. Evaluate each of the following expressions. a) p25 p16 b) p25 16 c) p144 + 25 d) p144 + p25 Solution: a) p25 p16 = 5 4 = 1 c) p144 + 25 = p169 = 13 b) p25 16 = p9 = 3 d) p144 + p25 = 12 + 5 = 17 . Denition: Let A be any real number. Then the third root of A (notation: p3 A) is the number that, if raised to the third power, the result is A.
  • Math Symbol Tables

    Math Symbol Tables

    APPENDIX A I Math symbol tables A.I Hebrew letters Type: Print: Type: Print: \aleph ~ \beth :J \daleth l \gimel J All symbols but \aleph need the amssymb package. 346 Appendix A A.2 Greek characters Type: Print: Type: Print: Type: Print: \alpha a \beta f3 \gamma 'Y \digamma F \delta b \epsilon E \varepsilon E \zeta ( \eta 'f/ \theta () \vartheta {) \iota ~ \kappa ,.. \varkappa x \lambda ,\ \mu /-l \nu v \xi ~ \pi 7r \varpi tv \rho p \varrho (} \sigma (J \varsigma <; \tau T \upsilon v \phi ¢ \varphi 'P \chi X \psi 'ljJ \omega w \digamma and \ varkappa require the amssymb package. Type: Print: Type: Print: \Gamma r \varGamma r \Delta L\ \varDelta L.\ \Theta e \varTheta e \Lambda A \varLambda A \Xi ~ \varXi ~ \Pi II \varPi II \Sigma 2: \varSigma E \Upsilon T \varUpsilon Y \Phi <I> \varPhi t[> \Psi III \varPsi 1ft \Omega n \varOmega D All symbols whose name begins with var need the amsmath package. Math symbol tables 347 A.3 Y1EX binary relations Type: Print: Type: Print: \in E \ni \leq < \geq >'" \11 « \gg \prec \succ \preceq \succeq \sim \cong \simeq \approx \equiv \doteq \subset c \supset \subseteq c \supseteq \sqsubseteq c \sqsupseteq \smile \frown \perp 1- \models F \mid I \parallel II \vdash f- \dashv -1 \propto <X \asymp \bowtie [Xl \sqsubset \sqsupset \Join The latter three symbols need the latexsym package. 348 Appendix A A.4 AMS binary relations Type: Print: Type: Print: \leqs1ant :::::; \geqs1ant ): \eqs1ant1ess :< \eqs1antgtr :::> \lesssim < \gtrsim > '" '" < > \lessapprox ~ \gtrapprox \approxeq ~ \lessdot <:: \gtrdot Y \111 «< \ggg »> \lessgtr S \gtr1ess Z < >- \lesseqgtr > \gtreq1ess < > < \gtreqq1ess \lesseqqgtr > < ~ \doteqdot --;- \eqcirc = .2..
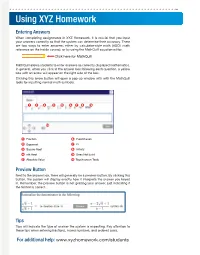
  • Using XYZ Homework

    Using XYZ Homework

    Using XYZ Homework Entering Answers When completing assignments in XYZ Homework, it is crucial that you input your answers correctly so that the system can determine their accuracy. There are two ways to enter answers, either by calculator-style math (ASCII math reference on the inside covers), or by using the MathQuill equation editor. Click here for MathQuill MathQuill allows students to enter answers as correctly displayed mathematics. In general, when you click in the answer box following each question, a yellow box with an arrow will appear on the right side of the box. Clicking this arrow button will open a pop-up window with with the MathQuill tools for inputting normal math symbols. 1 2 3 4 5 6 7 8 9 10 1 Fraction 6 Parentheses 2 Exponent 7 Pi 3 Square Root 8 Infinity 4 nth Root 9 Does Not Exist 5 Absolute Value 10 Touchscreen Tools Preview Button Next to the answer box, there will generally be a preview button. By clicking this button, the system will display exactly how it interprets the answer you keyed in. Remember, the preview button is not grading your answer, just indicating if the format is correct. Tips Tips will indicate the type of answer the system is expecting. Pay attention to these tips when entering fractions, mixed numbers, and ordered pairs. For additional help: www.xyzhomework.com/students ASCII Math (Calculator Style) Entry Some question types require a mathematical expression or equation in the answer box. Because XYZ Homework follows order of operations, the use of proper grouping symbols is necessary.
  • A Historical Survey of Methods of Solving Cubic Equations Minna Burgess Connor

    A Historical Survey of Methods of Solving Cubic Equations Minna Burgess Connor

    University of Richmond UR Scholarship Repository Master's Theses Student Research 7-1-1956 A historical survey of methods of solving cubic equations Minna Burgess Connor Follow this and additional works at: http://scholarship.richmond.edu/masters-theses Recommended Citation Connor, Minna Burgess, "A historical survey of methods of solving cubic equations" (1956). Master's Theses. Paper 114. This Thesis is brought to you for free and open access by the Student Research at UR Scholarship Repository. It has been accepted for inclusion in Master's Theses by an authorized administrator of UR Scholarship Repository. For more information, please contact [email protected]. A HISTORICAL SURVEY OF METHODS OF SOLVING CUBIC E<~UATIONS A Thesis Presented' to the Faculty or the Department of Mathematics University of Richmond In Partial Fulfillment ot the Requirements tor the Degree Master of Science by Minna Burgess Connor August 1956 LIBRARY UNIVERStTY OF RICHMOND VIRGlNIA 23173 - . TABLE Olf CONTENTS CHAPTER PAGE OUTLINE OF HISTORY INTRODUCTION' I. THE BABYLONIANS l) II. THE GREEKS 16 III. THE HINDUS 32 IV. THE CHINESE, lAPANESE AND 31 ARABS v. THE RENAISSANCE 47 VI. THE SEVEW.l'EEl'iTH AND S6 EIGHTEENTH CENTURIES VII. THE NINETEENTH AND 70 TWENTIETH C:BNTURIES VIII• CONCLUSION, BIBLIOGRAPHY 76 AND NOTES OUTLINE OF HISTORY OF SOLUTIONS I. The Babylonians (1800 B. c.) Solutions by use ot. :tables II. The Greeks·. cs·oo ·B.c,. - )00 A~D.) Hippocrates of Chios (~440) Hippias ot Elis (•420) (the quadratrix) Archytas (~400) _ .M~naeobmus J ""375) ,{,conic section~) Archimedes (-240) {conioisections) Nicomedea (-180) (the conchoid) Diophantus ot Alexander (75) (right-angled tr~angle) Pappus (300) · III.
  • 501 Algebra Questions 2Nd Edition

    501 Algebra Questions 2Nd Edition

    501 Algebra Questions 501 Algebra Questions 2nd Edition ® NEW YORK Copyright © 2006 LearningExpress, LLC. All rights reserved under International and Pan-American Copyright Conventions. Published in the United States by LearningExpress, LLC, New York. Library of Congress Cataloging-in-Publication Data: 501 algebra questions.—2nd ed. p. cm. Rev. ed. of: 501 algebra questions / [William Recco]. 1st ed. © 2002. ISBN 1-57685-552-X 1. Algebra—Problems, exercises, etc. I. Recco, William. 501 algebra questions. II. LearningExpress (Organization). III. Title: Five hundred one algebra questions. IV. Title: Five hundred and one algebra questions. QA157.A15 2006 512—dc22 2006040834 Printed in the United States of America 98765432 1 Second Edition ISBN 1-57685-552-X For more information or to place an order, contact LearningExpress at: 55 Broadway 8th Floor New York, NY 10006 Or visit us at: www.learnatest.com The LearningExpress Skill Builder in Focus Writing Team is comprised of experts in test preparation, as well as educators and teachers who specialize in language arts and math. LearningExpress Skill Builder in Focus Writing Team Brigit Dermott Freelance Writer English Tutor, New York Cares New York, New York Sandy Gade Project Editor LearningExpress New York, New York Kerry McLean Project Editor Math Tutor Shirley, New York William Recco Middle School Math Teacher, Grade 8 New York Shoreham/Wading River School District Math Tutor St. James, New York Colleen Schultz Middle School Math Teacher, Grade 8 Vestal Central School District Math Tutor
  • The Evolution of Equation-Solving: Linear, Quadratic, and Cubic

    The Evolution of Equation-Solving: Linear, Quadratic, and Cubic

    California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2006 The evolution of equation-solving: Linear, quadratic, and cubic Annabelle Louise Porter Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Mathematics Commons Recommended Citation Porter, Annabelle Louise, "The evolution of equation-solving: Linear, quadratic, and cubic" (2006). Theses Digitization Project. 3069. https://scholarworks.lib.csusb.edu/etd-project/3069 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. THE EVOLUTION OF EQUATION-SOLVING LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degre Master of Arts in Teaching: Mathematics by Annabelle Louise Porter June 2006 THE EVOLUTION OF EQUATION-SOLVING: LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino by Annabelle Louise Porter June 2006 Approved by: Shawnee McMurran, Committee Chair Date Laura Wallace, Committee Member , (Committee Member Peter Williams, Chair Davida Fischman Department of Mathematics MAT Coordinator Department of Mathematics ABSTRACT Algebra and algebraic thinking have been cornerstones of problem solving in many different cultures over time. Since ancient times, algebra has been used and developed in cultures around the world, and has undergone quite a bit of transformation. This paper is intended as a professional developmental tool to help secondary algebra teachers understand the concepts underlying the algorithms we use, how these algorithms developed, and why they work.
  • Just-In-Time 22-25 Notes

    Just-In-Time 22-25 Notes

    Just-In-Time 22-25 Notes Sections 22-25 1 JIT 22: Simplify Radical Expressions Definition of nth Roots p • If n is a natural number and yn = x, then n x = y. p • n x is read as \the nth root of x". p { 3 8 = 2 because 23 = 8. p { 4 81 = 3 because 34 = 81. p 2 • When n =p 2 we call it a \square root". However, instead of writing x, we drop the 2 and just write x. So, for example: p { 16 = 4 because 42 = 16. Domain of Radical Expressions • Howp do you find the even root of a negative number? For example, imagine the answer to 4 −16 is the number x. This means x4 = −16. The problem is, if we raise a number to the fourth power, we never get a negative answer: (2)4 = 2 · 2 · 2 · 2 = 16 (−2)4 = (−2)(−2)(−2)(−2) = 16 • Since there is no solution here for x, we say that the fourth root is undefined for negative numbers. • However, the same idea applies to any even root (square roots, fourth roots, sixth roots, etc) p If the expression contains n B where n is even, then B ≥ 0 . Properties of Roots/Radicals p • n xn = x if n is odd. p • n xn = jxj if n is even. p p p • n xy = n x n y (When n is even, x and y need to be nonnegative.) p q n x n x p • y = n y (When n is even, x and y need to be nonnegative.) p p m • n xm = ( n x) (When n is even, x needs to be nonnegative.) mp p p • n x = mn x 1 Examples p p 1.
  • Interactive Mathematics Program Curriculum Framework

    Interactive Mathematics Program Curriculum Framework

    Interactive Mathematics Program Curriculum Framework School: __Delaware STEM Academy________ Curricular Tool: _IMP________ Grade or Course _Year 1 (grade 9) Unit Concepts / Standards Alignment Essential Questions Assessments Big Ideas from IMP Unit One: Patterns Timeline: 6 weeks Interpret expressions that represent a quantity in terms of its Patterns emphasizes extended, open-ended Can students use variables and All assessments are context. CC.A-SSE.1 exploration and the search for patterns. algebraic expressions to listed at the end of the Important mathematics introduced or represent concrete situations, curriculum map. Understand that a function from one set (called the domain) reviewed in Patterns includes In-Out tables, generalize results, and describe to another set (called the range) assigns to each element of functions, variables, positive and negative functions? the domain exactly one element of the range. If f is a function numbers, and basic geometry concepts Can students use different and x is an element of its domain, then f(x) denotes the output related to polygons. Proof, another major representations of functions— of f corresponding to the input x. The graph of f is the graph theme, is developed as part of the larger symbolic, graphical, situational, of the equation y = f(x). CC.F-IF.1 theme of reasoning and explaining. and numerical—and Students’ ability to create and understand understanding the connections Recognize that sequences are functions, sometimes defined proofs will develop over their four years in between these representations? recursively, whose domain is a subset of the integers. For IMP; their work in this unit is an important example, the Fibonacci sequence is defined recursively by start.