1. Current Mirrors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Low Voltage Very High Impedance Current Mirror Circuit and Its Application
ISSN(Online): 2319-8753 ISSN (Print): 2347-6710 International Journal of Innovative Research in Science, Engineering and Technology (A High Impact Factor, Monthly, Peer Reviewed Journal) Visit: www.ijirset.com Vol. 8, Issue 2, February 2019 A Low Voltage Very High Impedance Current Mirror Circuit and Its Application Priya M.K.1, V.K.Vanitha Rugmoni2 M.Tech Scholar, Dept. of ECE, VJCET, Kerala, India1 Asst. Professor, Dept. of ECE, VJCET, Kerala, India2 ABSTRACT: Current mirror circuit has served as the basicbuilding block in analog circuit design since the introduction of integrated circuits. In this paper, “A Very high impedance current mirror, operating in reduced power supply which does not use any additional biasing circuit and its application” is proposed. The design uses a high swing super Wilson current mirror which has negative feedback. A feedback action is used to force the input and output currents to be equal. The output current is expected to be mirrored with a transfer error less than 1% when the input current is increased from 5μA to 40μ A. As an application, the current mirror circuit has been used in the design of a high gain, improved output swing differential amplifier. A telescopic differential amplifier is chosen for designing since it is used in low power application. A comparative study of different current mirror circuits and amplifier is also made. The output swing of the circuit is improved than what is expected. KEYWORDS: Current mirror, Wilson current mirror, Output Impedance, CMRR,Telescopic Differential Amplifier I. INTRODUCTION In the early 1980s many experts predicted the demise of analog circuits. -

Current Mirrors
Current mirrors Current mirrors are important blocks in electronics. They are widely used in several applications and chips, the operational amplifier being one of them. Current mirrors consist of two branches that are parallel to each other and create two approximately equal currents. This is why these circuits are called current mirrors. These currents are used to load other stages in circuits and they are designed in such a way so that current is constant and independent of loading. Current mirrors come in different varieties: Simple current mirror (BJT and MOSFET) Base current corrected simple current mirror Widlar current source Wilson current mirror (BJT and MOSFET) Cascoded current mirror (BJT and MOSFET) For best performance, transistors should be matched, temperature should be the same for all devices and collector-base/drain-gate voltages should also be matched. This will provide equal currents on both sides of the current mirror. All of the circuits have a compliance voltage which is the minimum output voltage required to maintain correct circuit operation: the BJT should be in the active/linear region and the MOSFET should be in the active/saturation region. 1 www.ice77.net Simple current mirror Two implementations exist for the simple current mirror: BJT and MOSFET. BJT The BJT implementation of the simple current mirror is used as a block in the operational amplifier. VCC Vo 3.600V 1.472mA R1 VCC Vo IREF Io I 2k 3.600V 650.0mV V1 V2 Q1 3.6Vdc 0.65Vdc 1.425mA Q2 1.425mA 1.425mA 1.472mA 0V 23.47uA 0V I 23.47uA 655.3mV -

EE 508 OTA Laboratory Experiment
EE 508 OTA Laboratory Experiment The Operational Transconductance Amplifier is widely used in integrated amplifier and filter applications. There are also some specific discrete applications where the device can be used. Irrespective whether used in integrated or discrete applications, issues surrounding design and performance are mostly common. There are several discrete OTAs on the market. The CA 3080 and 3092, introduced by RCA, were the first. More recent, the NE 5517 has become quite popular. It is a DUAL OTA with tail bias current control. Another useful OTA is the LM13700 manufactured by National Semiconductor. These devices are particularly useful in the design of voltage or current controlled applications. One of the particularly attractive applications of the OTA is in the design of voltage-controller or current-controlled amplifiers and filters where by a dc voltage or a dc current can be used to control or adjust key characteristics of a filter such as the band edges, the mid-band gain, or the bandwidth. An attached article written a number of years ago is useful at describing some of the signal conditioning strategies needed to used the OTA along with methods of building voltage controlled filters. Part 1 Design and test a voltage controlled amplifier. The gain of the amplifier should be adjustable from +1 to +10 as a control voltage is changed between 1V and 2V Part 2 Design and test a voltage controlled bandpass filter. The bandpass filter should have a Q of 5 and the resonant frequency should be adjustable between 1KHz and 20KHz as the dc control voltage changes between 1V and 2V. -

Electronically Tunable Multi-Terminal Floating Nullor and Its Applications
RADIOENGINEERING, VOL. 17, NO. 4, DECEMBER 2008 3 Electronically Tunable Multi-Terminal Floating Nullor and Its Applications Worapong TANGSRIRAT Faculty of Engineering , King Mongkut’s Institute of Technology Ladkrabang (KMITL), Chlongkrung Rd., Ladkrabang, Bangkok 10520, Thailand [email protected] Abstract. A realization scheme of an electronically tun- conventional operational amplifier (op-amp) and the com- able multi-terminal floating nullor (ET-MTFN) is de- mercial operational transconductance amplifier (OTA) as scribed in this paper. The proposed circuit mainly employs the major active component, these configurations are less a transconductance amplifier, an improved translinear appropriate for high-frequency applications and uneco- cell, two complementary current mirrors with variable nomical for applying to an IC fabrication. Recently, there current gain and improved Wilson current mirrors, which has been much effort to construct the FTFN with multi- provide an electronic tuning of the current gain. The va- output terminals [11]. In general, if the multi-output type lidity of the performance of the scheme is verified through active components are employed, the number of compo- PSPICE simulation results. Example applications nents that constitutes a configuration may be reduced and employing the proposed ET-MTFN as an active element the resulting circuit may be miniaturized [12]. demonstrate that the circuit properties can be varied by This paper describes an alternative realization scheme electronic means. for realizing a monolithically integrable multi-output FTFN or multi-terminal floating nullor (MTFN), which provides electronically variable current gain. The proposed circuit is Keywords based on the use of a transconductance amplifier, an im- proved translinear cell and some current mirrors. -

Widlar Current Mirror Design Using BJT-Memristor Circuits
1 Widlar Current Mirror Design Using BJT-Memristor Circuits Amanzhol Daribay and Irina Dolzhikova, Electrical and Computer Engineering Department, Nazarbayev University, Astana, Kazakhstan [email protected], [email protected] Abstract—This paper presents a description of basic current is calculated to be Rout = V=I = 100=1mA = 100kOhm. mirror (CM), Widlar current mirror, fourth circuit element It is known that Basic BJT CM is aimed to supply nearly (memristor) and an analysis of Widlar Configuration with integrated memristor. The analysis has been performed by comparing a modified configuration with a simple circuit of Widlar CM. The focus of analysis were a power dissipation, a Total Harmonic Distortion and a chip-surface. The results has shown that a presence of memristor in the Widlar CM decreases the chip-surface area and the deviation of the signal in the circuit from a fundamental frequency. Although the analysis of power dissipation has also been conducted, there is no definite conclusion about the power losses in the circuit because of the memristor model. Index Terms—current mirror, Widlar current source, bjt- memristor circuit, power analysis, noise analysis, total harmonic distortion. Figure 2. Basic BJT CM schematic I. INTRODUCTION constant current to a load over a wide range of load resistances. A. Basic Current Mirror Since in LTSpice it is more convenient to change some output over varying DC voltage with specified increment in Basically, current mirrors (CMs) are used to mirror a LTSpice, in order to observe mirrored current Ic(Q2) , it has reference current multiple times from one designated source been established different loading conditions by changing load into another consuming circuits. -

Section G2: Current Sources and Active Loads
Section G2: Current Sources and Active Loads The transistor biasing techniques introduced in earlier sections are not suitable for the design of IC amplifiers since, even for a relatively simple multistage amplification system, many resistors and large capacitors are required. This is problematic for a couple of reasons, most importantly the cost of chip “real-estate” and fabrication concerns. However, fabrication of simple transistors has become cheap and easy, as well as providing the ability to have a large number of transistors with matched characteristics. Therefore, biasing in integrated circuit (IC) design is based on the use of transistors configured to act as constant current sources. On a multistage amplifier IC chip, a constant dc current source is generated at one location and is then reproduced at different locations for biasing the various amplification stages. The major advantages to this approach include: ¾ the requirement for resistors, coupling capacitors and bypass capacitors is removed; and ¾ the biasing of the multiple stages track each other in case of parameter changes, such as voltage supply or temperature fluctuations. In this section, we will be looking at several methods of providing a constant dc current source for amplifier biasing using simple transistor configurations. Many of the circuits used to generate bias currents are also used for providing large resistances for IC applications. The active loads created in this manner, as well as the dc current sources, are small and easy to fabricate on IC chips. Diode Connected Transistors Before we get into current sources, let’s take a little bit to look at the details of the diode-connected transistor. -

Current Mirrors
Chapter 20 Current Mirrors In this chapter we turn our attention towards the design, layout, and simulation of current mirrors (a circuit that sources [or sinks] a constant current). As we observed back in Fig. 9.1, and the associated discussion, the ideal output resistance, r0, of a current source is infinite. Achieving high output resistance (meaning that the output current doesn't vary much with the voltage across the current source) will be the main focus of this chapter. It's very important that the reader first understand the material in Ch. 9 concerning the selection of biasing currents and device sizes and how they affect the gain/speed of the analog circuits. We'll use the parameters found in Tables 9.1 and 9.2 in many of the examples in this chapter. 20.1 The Basic Current Mirror The basic NMOS current mirror, made using Ml and M2, is seen in Fig. 20.1. Let's assume that Ml and M2 have the same width and length and note that VGSl = VDSI = VGS2. Because the MOSFETs have the same gate-source voltages, we expect (neglecting channel-length modulation) them to have the same drain current. If the two resistors in the drains of M1/M2 are equal, the drain of M2 will be at the same potential as the drain of Ml (this is important). By matching the size, Vcs , and ID of two transistors, we are assured that the two MOSFETs have the same drain-source voltage, (VGS\ = VDS\ = VGSI = VDSI)- VDD VDD S S Figure 20.1 A basic current mirror. -

Current Mirrors
Current mirrors An often-used circuit applying the bipolar junction transistor is the so-called current mirror, which serves as a simple current regulator, supplying nearly constant current to a load over a wide range of load resistances. We know that in a transistor operating in its active mode, collector current is equal to base current multiplied by the ratio β. We also know that the ratio between collector current and emitter current is called α. Because collector current is equal to base current multiplied by β, and emitter current is the sum of the base and collector currents, α should be mathematically derivable from β. If you do the algebra, you'll find that α = β/(β+1) for any transistor. We've seen already how maintaining a constant base current through an active transistor results in the regulation of collector current, according to the β ratio. Well, the α ratio works similarly: if emitter current is held constant, collector current will remain at a stable, regulated value so long as the transistor has enough collector-to-emitter voltage drop to maintain it in its active mode. Therefore, if we have a way of holding emitter current constant through a transistor, the transistor will work to regulate collector current at a constant value. Remember that the base-emitter junction of a BJT is nothing more than a PN junction, just like a diode, and that the “diode equation” specifies how much current will go through a PN junction given forward voltage drop and junction temperature: If both junction voltage and temperature are held constant, then the PN junction current will be constant. -

Current Mirror Circuit with Accurate Mirror Gain For
CURRENT MIRROR CIRCUIT WITH ACCURATE MIRROR GAIN FOR LOW β TRANSISTORS∗ Huiting Chen∗∗, Frank Whiteside∗∗∗, Randall Geiger∗∗ ∗∗Iowa State University *** Dallas Semiconductor Corp. Ames, IA 50011, USA Dallas, TX 75244, USA ABSTRACT across the base-emitter terminals of Q2. If Q1 and Q2 are matched, the emitter currents of Q1 and Q2 will be the same. If A new current mirror with accurate mirror gain for low β the base currents of Q1 and Q2 are negligibly small, it follows transistors is presented. The new current mirror employs a that the output current Iout will be the same as the input current. If cascoded output stage to provide high output impedance. High the base currents are not negligibly small, this current mirror has mirror gain accuracy is achieved by using a split-collector an output current Iout that is smaller than the input current transistor to compensate for base currents of the source-coupled because a current whose value is equal to the sum of base transistor pair. The split factor is dependent on the desired mirror currents of Q1 and Q2 is subtracted from the input current before gain and the nominal β value. it reaches the collector of Q1. Taking these two base currents into account and assuming Q1 and Q2 are perfectly matched, the 1. INTRODUCTION current mirror gain is given by I 1 (1) The current mirror is one of the most basic building blocks used A = out = I 2 in linear IC design. Although CMOS process have become in 1+ β dominant in applications requiring a large amount of digital circuitry on a chip, BJT circuits in either Bi-MOS or bipolar where β is the transistor current gain of Q1 and Q2. -

Operational Transconductance Amplifier
Operational transconductance amplifier Operational transconductance amplifier (OTA) is a monolithic direct coupled differential voltage controlled current source. They have a differential input and an output that is single-ended. OTA are described by transconductance gain gm instead of voltage-gain. They are very suitable for a broad variety of applications because they are similar to op-amp. As opposed to the operational amplifier, OTA has an ability to change gain which provides greater flexibility in design of analog circuits . The transconductance of an OTA can be linearly controlled by changing bias current (Ib) or voltage (Vb) through an extra control terminal. ANALOGNA ELEKTRONSKA KOLA Operational transconductance amplifier Differences between OTA and operational amplifier: OTA has an adjustable gain in contrast to the OP-amp. Network equations of the OTA circuits contain besides the values of passive elements, transconductance gm as an additional unknown. The output impedance of an OTA is very high in contrast to the operational amplifier . Consequently, OTA behaves as a current source at the output. As opposed to the linear OP-amp circuits, linear OTA circuits does not necessary use external negative feedback ANALOGNA ELEKTRONSKA KOLA Operational transconductance amplifier Characteristics of an ideal OTA Infinite input resistance Rin →∞ Infinite output resistance Ro→∞ Infinite frequency bandwidth ω0→∞ The amplifier is ideally balanced: I 0=0 when V1=V 2 Transconductance gm is finite and controllable with the bias current IB ANALOGNA ELEKTRONSKA KOLA Operational transconductance amplifier Characteristics of a real OTA Finite input resistance Rin Finite output resistance R O Offset voltage Amplifies common mode signal Finite bandwidth gm0 ⋅ωa gm (s) = s +ωa Open loop transconductance is constant at lower frequencies. -

Implementation and Applications of Current Sources and Current Receivers
®APPLICATION BULLETIN Mailing Address: PO Box 11400 • Tucson, AZ 85734 • Street Address: 6730 S. Tucson Blvd. • Tucson, AZ 85706 Tel: (602) 746-1111 • Twx: 910-952-111 • Telex: 066-6491 • FAX (602) 889-1510 • Immediate Product Info: (800) 548-6132 IMPLEMENTATION AND APPLICATIONS OF CURRENT SOURCES AND CURRENT RECEIVERS This application guide is intended as a source book for the This is not an exhaustive collection of circuits, but a com- design and application of: pendium of preferred ones. Where appropriate, suggested ● Current sources part numbers and component values are given. Where added ● Current sinks components may be needed for stability, they are shown. ● Floating current sources Experienced designers may elect to omit these components ● Voltage-to-current converters in some applications, but less seasoned practitioners will be (transconductance amplifiers) able to put together a working circuit free from the frustra- ● Current-to-current converters (current mirrors) tion of how to make it stable. ● Current-to-voltage converters The applications shown are intended to inspire the imagina- (transimpedance amplifiers) tion of designers who will move beyond the scope of this work. R. Mark Stitt (602) 746-7445 CONTENTS DEAD BAND CIRCUITS USING CURRENT REFERENCE ....... 14 DESIGN OF FIXED CURRENT SOURCES BIDIRECTIONAL CURRENT SOURCES .................................... 16 REF200 IC CURRENT SOURCE DESCRIPTION PIN STRAPPING REF200 FOR 50µA—400µA..2 LIMITING CIRCUITS USING RESISTOR PROGRAMMABLE CURRENT SOURCES BIDIRECTIONAL CURRENT SOURCES .................................... 16 AND SINKS USING REF200 AND ONE EXTERNAL OP AMP: PRECISION TRIANGLE WAVEFORM GENERATOR Current Source or Sink With Compliance to USING BIDIRECTIONAL CURRENT SOURCES ....................... 17 Power Supply Rail and Current Out >100µA .......................... 4 DUTY CYCLE MODULATOR USING Current Source or Sink With Any Current Out ..................... -
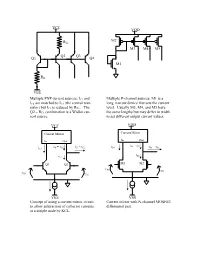
Multiple PNP Current Sources; IC3 and IC4 Are Matched To
VCC VDD R M2 E2 M3 M4 M5 Q2 Q3 Q1 Q4 M1 RB VEE Multiple PNP current sources; IC3 and Multiple P-channel sources: M1 is a IC4 are matched to IC1 (the control tran- long, narrow device that sets the current sistor) but IC2 is reduced by RE2 . The level. Usually M3, M4, and M5 have Q2 – RE2 combination is a Widlar cur- the same lengths but may differ in width rent source. to set different output current values. VCC VDD Current Mirror Current Mirror In Out In Out iM = iD1 iM = iC1 iC1 – iC2 iD1 iD1 – iD2 iC1 iD2 iC2 Q1 Q2 M1 M2 vIN1 vIN2 v IN1 vIN2 VEE VSS Concept of using a current mirror circuit Current mirror with N-channel MOSFET to allow subtraction of collector currents differential pair. at a simple node by KCL. VCC iOUT RBIAS Q1 iOUT Q2 iIN Q1 Q2 RE VEE VEE Widlar current source, for which The most basic current mirror with hi kT ⎛⎞IC1 FE IN I = ln . The collector cur- iOUT = and an output resistance C 2 ⎜⎟ h + 2 qREC⎝⎠I 2 FE rent of Q2 may be much lower than Q1 VVCE + A equal to rO2 = . with only a modest value for RE. IC VCC iIN i iIN i OUT OUT Q3 Q3 Q1 Q2 Q1 Q2 VEE VEE Current mirror using a common collector stage to balance input and output. Output Wilson current mirror –this has a much impedance is still rO2. The minimum higher output resistance from the output voltage is very low – VCESAT of cascoding effect of Q3.