DOCSLIB.ORG

Solutions: Environmental Chemistry - a Global Perspective 4Th Edition

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Solutions: Environmental Chemistry - a Global Perspective 4Th Edition Solutions: Environmental Chemistry - a global perspective 4th Edition Chapter 11 Gases in water PROBLEMS/SOLUTIONS 1. Lake Titicaca is situated at an altitude of 3810 m in the Bolivian Andes. Determine the atmospheric pressure and calculate the solubility of oxygen in the lake at a temperature of 5ºC. (The Henry’s law constant at 5ºC is 1.9 × 10–8 mol L–1 Pa–1) Solution Since we are given Henry's law constant, this suggests we need to calculate a partial pressure for oxygen, which will then allow for the calculation of the concentration of oxygen in mol L-1. But first we need a total pressure for the altitude given. Here we will assume the mixing ratio for oxygen remains constant (see Chapter 2, Equation 2.3) with increasing altitude. o M g h / R T a Ph P e The total pressure at 3810 m (Ph) is: -(0.029 x 9.81 x 3810) / (8.315 x 278) P3810 = 101 325 e P3810 = 63 394 Pa (1 atm = 101 325 Pa) or Ph = 0.626 atm Assume the mixing ratio of O2 is constant at 0.2095 (Chapter 2, Table 2.1a) At 5ºC the vapour pressure of water is approximately 870 Pa (Chapter 9, Table 9.3). 63 394 Pa - 870 Pa = 62 524 Pa (dry atmosphere) 62 524 Pa x 0.2095 = 13 099 Pa (partial pressure of O2) The partial pressure of oxygen is then 13 099 Pa at 3810 m. To calculate the oxygen concentration use Henry’s Law; [Gl] = KH x Pg -8 -1 -1 [O2] = 1.9 x 10 mol L Pa x 13 099 Pa -4 -1 -1 [O2] = 2.5 x 10 mol L (or 8.0 mg L ) The solubility of oxygen at 3810 m and 5ºC is 8.0 mg L-1. This compares to a value of 12.8 mg L-1 at sea level and 5ºC. 2. The solubility of oxygen in water at 25ºC is approximately 8.5 mg L–1. At Pº and the same temperature, what is the volume of oxygen gas occupied by 8.5 mg of oxygen? 95 Solutions: Environmental Chemistry - a global perspective 4th Edition Chapter 11 Gases in water Solution Use PV = nRT (at P, P = 1.00 atm, O2 mixing ratio is 20.95% giving an oxygen pressure of 0.2095 atm, T = 298 K, R = 0.08206 L atm mol-1 K-1). The mass of oxygen being considered is 8.5 mg, which is converted to moles. 8.5 mg 1000 mg g-1 = 0.0085 g -1 n = 0.0085 g 32.0 g mol = 0.000265625 mol O2 The volume of O2 can be calculated using the ideal gas law: V = nRT/P = 0.000265625 mol x 0.08206 L atm mol-1 K-1 x 298 K / 0.2095 atm V = 0.006496 L atm / 0.2095 atm -1 V = 0.0310 L (multiply by 1000 mL L to convert to mL) The volume of gas from 8.5 mg of O2 (g) at P and 25C is 31 mL. 3. At 30ºC, the solubility of oxygen in water is 7.5 mg L–1. Consider a water body at that temperature containing 7.0 mg L–1 oxygen. By photosynthesis, 1.5 mg of carbon (as carbon dioxide) is converted to organic biomass ({CH2O}) during a single hot day. Is the amount of oxygen produced at the same time sufficient to exceed its aqueous solubility? Solution The process under consideration is hν CO2 (g) + H2O (l) → {CH2O} + O2 (aq) 1.5 mg of C (as CO2) gives: -1 0.0015 g ÷ 12.011 g mol = 0.000125 mol C (or CO2, or O2) -1 0.000125 mol x 32 000 mg mol = 4.0 mg (O2) The amount of O2 produced from 1.5 mg of C is 4.0 mg. Starting from the original concentration of 7.0 mg -1 L O2, the quantity of oxygen produced would only require 8 L of water to reach saturation. Any larger volume would mean that the water would not be saturated. Therefore, the answer to the question requires knowledge of the volume of water under consideration. The amount of oxygen produced at the same time is not sufficient to exceed its aqueous solubility, assuming that the water body was larger than 8 L. 4. Thermal power plants, whether powered by fossil fuel or nuclear energy, discharge large quantities of cooling water to a lake or river. Discuss the meaning of thermal pollution in the context of this chapter. 96 Solutions: Environmental Chemistry - a global perspective 4th Edition Chapter 11 Gases in water Solution Increasing the temperature of the water (thermal pollution) by discharge of heat through cooling water will cause gases to be less soluble. We saw for oxygen that the range of temperatures from 5ºC to 30ºC caused its solubility to range from 12.4 mg L-1 to 7.5 mg L-1 (Section 11.1). At the higher temperature the decreased amount of oxygen could have an impact on the water quality in terms of supporting fish life. The heat added through the cooling water is thermal pollution that is causing the death of fish, the same way a chemical toxin added to water could also cause an immediate response by killing fish. 5. The estimated atmospheric carbon dioxide concentration in the Northern Hemisphere in 1950 was 310 ppmv. It may be predicted with some certainty that the concentration in 2020 will be 406 ppmv. Calculate the pH of pure rain that would be in equilibrium with the carbon dioxide in each of the 2 years cited, and comment on the contribution that carbon dioxide makes towards precipitation acidity. Solution Assume total pressure is Pº = 101 325 Pa and temperature is 298 K. The mixing ratios given (in units of ppmv) are also a mole fraction (x 106), and therefore, the partial pressure of carbon dioxide is given by: -6 310 ppmv CO2 = 310 x 10 x 101 325 Pa = 31.4 Pa -7 -1 -1 Henry’s Law constant for CO2 is 3.3 x 10 mol L Pa (Table 11.1) Using Henry’s Law : [G]l = KHPg -7 -1 -1 -5 -1 [CO2](aq) = 3.3 x 10 mol L Pa x 31.4 Pa = 1.04 x 10 mol L H2O (l) + CO2 (aq) → H2CO3 (aq) -7 Ka = 4.5 x 10 + - H2CO3 (aq) ↔ H (aq) + HCO3 (aq) - + [HCO3 ][H ] -7 Ka = ----------------- = 4.5 x 10 [CO2] -5 -1 - + Assume [CO2] = 1.04 x 10 mol L , and that [HCO3 ] = [H ] Solve for [H+], [H+] = 2.16 x 10-6 pH = 5.67 Repeat the calculation for 406 ppmv: result is pH = 5.61 The increase in CO2 concentration in the atmosphere from 310 ppmv to 406 ppmv over the seventy year period will cause a slight decrease (0.06 pH units) in the pH of pure rainfall. This decrease in pH (increase in acidity) is negligible compared to the pH changes experienced from nitrogen and sulphur oxides emitted from anthropogenic sources over this same time period, but the trend is concerning. 97 Solutions: Environmental Chemistry - a global perspective 4th Edition Chapter 11 Gases in water 6. One of the alternative expressions for Henry’s law when applied to oxygen is P K X O2 H O2 where P is the pressure of oxygen in the gas phase and X is its mole fraction in solution. O2 O2 Calculate the value of Henry’s law constant, KH , at 25ºC in units of MPa. Solution Assume both the air and water temperature are 25ºC and the total pressure is equal to 101 325 Pa. ’ PO2 = KH x XO2 At 25ºC there is 8.5 mg L-1 dissolved oxygen in water. -4 the number of moles of O2 in 1 L = 2.66 x 10 , (total moles in 1L ~ 55.5 mol) -4 -6 XO2 = 2.66 x 10 ÷ 55.5 = 4.79 x 10 The partial pressure of O2 is: 101 325 Pa - 3200 Pa (correction for moisture, using Figure 8.2 or Table 9.3) = 98 125 Pa PO2 = 98 125 x 0.2095 = 20 557 Pa -6 9 KH’ = 20 557 Pa ÷ 4.79 x 10 = 4.29 x 10 Pa 6 or KH’ = 4290 MPa (the prefix M = 1 x 10 , Appendix C.2) Henry's Law (for O2) becomes: PO2 = 4290 MPa x XO2 7. If sulfur dioxide (SO2) is bubbled through water, the following reactions take place If the SO2 is in a gas stream at a concentration of 10.9 ppbv, while the total gas pressure is 1 atm and the pH of the resulting solution is 4.89, what must the Henry’s law constant be for SO2 in water at this temperature? Solution -8 -3 10.9 ppbv = 1.09 x 10 x 101325 Pa = 1.1 x 10 Pa SO2 + -5 - + given [H ] = 1.29 x 10 = [HSO3 ], assuming only source of H is from H2SO3 98 Solutions: Environmental Chemistry - a global perspective 4th Edition Chapter 11 Gases in water -2 -5 2 1.23 x 10 = (1.29 x 10 ) / [H2SO3] -8 -1 [H2SO3] = 1.35 x 10 mol L -8 -1 Assume [H2SO3] = [SO2] = 1.35 x 10 mol L [SO2] = KH x PSO2 -8 -1 -3 KH = 1.35 x 10 mol L / 1.1 x 10 Pa -5 -1 -1 = 1.23 x 10 mol L Pa -5 -1 -1 The Henry’s law constant for SO2 in water at this temperature was found to be 1.23 x 10 mol L Pa 8.
Load more

Recommended publications
  • Development Team
    Paper No: 16 Environmental Chemistry Module: 01 Environmental Concentration Units Development Team Prof. R.K. Kohli Principal Investigator & Prof. V.K. Garg & Prof. Ashok Dhawan Co- Principal Investigator Central University of Punjab, Bathinda Prof. K.S. Gupta Paper Coordinator University of Rajasthan, Jaipur Prof. K.S. Gupta Content Writer University of Rajasthan, Jaipur Content Reviewer Dr. V.K. Garg Central University of Punjab, Bathinda Anchor Institute Central University of Punjab 1 Environmental Chemistry Environmental Environmental Concentration Units Sciences Description of Module Subject Name Environmental Sciences Paper Name Environmental Chemistry Module Name/Title Environmental Concentration Units Module Id EVS/EC-XVI/01 Pre-requisites A basic knowledge of concentration units 1. To define exponents, prefixes and symbols based on SI units 2. To define molarity and molality 3. To define number density and mixing ratio 4. To define parts –per notation by volume Objectives 5. To define parts-per notation by mass by mass 6. To define mass by volume unit for trace gases in air 7. To define mass by volume unit for aqueous media 8. To convert one unit into another Keywords Environmental concentrations, parts- per notations, ppm, ppb, ppt, partial pressure 2 Environmental Chemistry Environmental Environmental Concentration Units Sciences Module 1: Environmental Concentration Units Contents 1. Introduction 2. Exponents 3. Environmental Concentration Units 4. Molarity, mol/L 5. Molality, mol/kg 6. Number Density (n) 7. Mixing Ratio 8. Parts-Per Notation by Volume 9. ppmv, ppbv and pptv 10. Parts-Per Notation by Mass by Mass. 11. Mass by Volume Unit for Trace Gases in Air: Microgram per Cubic Meter, µg/m3 12.
    [Show full text]
  • The Vertical Distribution of Soluble Gases in the Troposphere
    UC Irvine UC Irvine Previously Published Works Title The vertical distribution of soluble gases in the troposphere Permalink https://escholarship.org/uc/item/7gc9g430 Journal Geophysical Research Letters, 2(8) ISSN 0094-8276 Authors Stedman, DH Chameides, WL Cicerone, RJ Publication Date 1975 DOI 10.1029/GL002i008p00333 License https://creativecommons.org/licenses/by/4.0/ 4.0 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Vol. 2 No. 8 GEOPHYSICAL RESEARCHLETTERS August 1975 THE VERTICAL DISTRIBUTION OF SOLUBLE GASES IN THE TROPOSPHERE D. H. Stedman, W. L. Chameides, and R. J. Cicerone Space Physics Research Laboratory Department of Atmospheric and Oceanic Science The University of Michigan, Ann Arbor, Michigan 48105 Abstrg.ct. The thermodynamic properties of sev- Their arg:uments were based on the existence of an eral water-soluble gases are reviewed to determine HC1-H20 d•mer, but we consider the conclusions in- the likely effect of the atmospheric water cycle dependeht of the existence of dimers. For in- on their vertical profiles. We find that gaseous stance, Chameides[1975] has argued that HNO3 HC1, HN03, and HBr are sufficiently soluble in should follow the water-vapor mixing ratio gradi- water to suggest that their vertical profiles in ent, based on the high solubility of the gas in the troposphere have a similar shape to that of liquid water. In this work, we generalize the water va•or. Thuswe predict that HC1,HN03, and moredetailed argumentsof Chameides[1975] and HBr exhibit a steep negative gradient with alti- suggest which species should exhibit this nega- tude roughly equal to the altitude gradient of tive gradient and which should not.
    [Show full text]
  • Package 'Marelac'
    Package ‘marelac’ February 20, 2020 Version 2.1.10 Title Tools for Aquatic Sciences Author Karline Soetaert [aut, cre], Thomas Petzoldt [aut], Filip Meysman [cph], Lorenz Meire [cph] Maintainer Karline Soetaert <[email protected]> Depends R (>= 3.2), shape Imports stats, seacarb Description Datasets, constants, conversion factors, and utilities for 'MArine', 'Riverine', 'Estuarine', 'LAcustrine' and 'Coastal' science. The package contains among others: (1) chemical and physical constants and datasets, e.g. atomic weights, gas constants, the earths bathymetry; (2) conversion factors (e.g. gram to mol to liter, barometric units, temperature, salinity); (3) physical functions, e.g. to estimate concentrations of conservative substances, gas transfer and diffusion coefficients, the Coriolis force and gravity; (4) thermophysical properties of the seawater, as from the UNESCO polynomial or from the more recent derivation based on a Gibbs function. License GPL (>= 2) LazyData yes Repository CRAN Repository/R-Forge/Project marelac Repository/R-Forge/Revision 205 Repository/R-Forge/DateTimeStamp 2020-02-11 22:10:45 Date/Publication 2020-02-20 18:50:04 UTC NeedsCompilation yes 1 2 R topics documented: R topics documented: marelac-package . .3 air_density . .5 air_spechum . .6 atmComp . .7 AtomicWeight . .8 Bathymetry . .9 Constants . 10 convert_p . 11 convert_RtoS . 11 convert_salinity . 13 convert_StoCl . 15 convert_StoR . 16 convert_T . 17 coriolis . 18 diffcoeff . 19 earth_surf . 21 gas_O2sat . 23 gas_satconc . 25 gas_schmidt . 27 gas_solubility . 28 gas_transfer . 31 gravity . 33 molvol . 34 molweight . 36 Oceans . 37 redfield . 38 ssd2rad . 39 sw_adtgrad . 40 sw_alpha . 41 sw_beta . 42 sw_comp . 43 sw_conserv . 44 sw_cp . 45 sw_dens . 47 sw_depth . 49 sw_enthalpy . 50 sw_entropy . 51 sw_gibbs . 52 sw_kappa .
    [Show full text]
  • Calculation Exercises with Answers and Solutions
    Atmospheric Chemistry and Physics Calculation Exercises Contents Exercise A, chapter 1 - 3 in Jacob …………………………………………………… 2 Exercise B, chapter 4, 6 in Jacob …………………………………………………… 6 Exercise C, chapter 7, 8 in Jacob, OH on aerosols and booklet by Heintzenberg … 11 Exercise D, chapter 9 in Jacob………………………………………………………. 16 Exercise E, chapter 10 in Jacob……………………………………………………… 20 Exercise F, chapter 11 - 13 in Jacob………………………………………………… 24 Answers and solutions …………………………………………………………………. 29 Note that approximately 40% of the written exam deals with calculations. The remainder is about understanding of the theory. Exercises marked with an asterisk (*) are for the most interested students. These exercises are more comprehensive and/or difficult than questions appearing in the written exam. 1 Atmospheric Chemistry and Physics – Exercise A, chap. 1 – 3 Recommended activity before exercise: Try to solve 1:1 – 1:5, 2:1 – 2:2 and 3:1 – 3:2. Summary: Concentration Example Advantage Number density No. molecules/m3, Useful for calculations of reaction kmol/m3 rates in the gas phase Partial pressure Useful measure on the amount of a substance that easily can be converted to mixing ratio Mixing ratio ppmv can mean e.g. Concentration relative to the mole/mole or partial concentration of air molecules. Very pressure/total pressure useful because air is compressible. Ideal gas law: PV = nRT Molar mass: M = m/n Density: ρ = m/V = PM/RT; (from the two equations above) Mixing ratio (vol): Cx = nx/na = Px/Pa ≠ mx/ma Number density: Cvol = nNav/V 26 -1 Avogadro’s
    [Show full text]
  • Lecture 3. the Basic Properties of the Natural Atmosphere 1. Composition
    Lecture 3. The basic properties of the natural atmosphere Objectives: 1. Composition of air. 2. Pressure. 3. Temperature. 4. Density. 5. Concentration. Mole. Mixing ratio. 6. Gas laws. 7. Dry air and moist air. Readings: Turco: p.11-27, 38-43, 366-367, 490-492; Brimblecombe: p. 1-5 1. Composition of air. The word atmosphere derives from the Greek atmo (vapor) and spherios (sphere). The Earth’s atmosphere is a mixture of gases that we call air. Air usually contains a number of small particles (atmospheric aerosols), clouds of condensed water, and ice cloud. NOTE : The atmosphere is a thin veil of gases; if our planet were the size of an apple, its atmosphere would be thick as the apple peel. Some 80% of the mass of the atmosphere is within 10 km of the surface of the Earth, which has a diameter of about 12,742 km. The Earth’s atmosphere as a mixture of gases is characterized by pressure, temperature, and density which vary with altitude (will be discussed in Lecture 4). The atmosphere below about 100 km is called Homosphere. This part of the atmosphere consists of uniform mixtures of gases as illustrated in Table 3.1. 1 Table 3.1. The composition of air. Gases Fraction of air Constant gases Nitrogen, N2 78.08% Oxygen, O2 20.95% Argon, Ar 0.93% Neon, Ne 0.0018% Helium, He 0.0005% Krypton, Kr 0.00011% Xenon, Xe 0.000009% Variable gases Water vapor, H2O 4.0% (maximum, in the tropics) 0.00001% (minimum, at the South Pole) Carbon dioxide, CO2 0.0365% (increasing ~0.4% per year) Methane, CH4 ~0.00018% (increases due to agriculture) Hydrogen, H2 ~0.00006% Nitrous oxide, N2O ~0.00003% Carbon monoxide, CO ~0.000009% Ozone, O3 ~0.000001% - 0.0004% Fluorocarbon 12, CF2Cl2 ~0.00000005% Other gases 1% Oxygen 21% Nitrogen 78% 2 • Some gases in Table 3.1 are called constant gases because the ratio of the number of molecules for each gas and the total number of molecules of air do not change substantially from time to time or place to place.
    [Show full text]
  • Interactions Between Polymers and Nanoparticles : Formation of « Supermicellar » Hybrid Aggregates
    1 Interactions between Polymers and Nanoparticles : Formation of « Supermicellar » Hybrid Aggregates J.-F. Berret@, K. Yokota* and M. Morvan, Complex Fluids Laboratory, UMR CNRS - Rhodia n°166, Cranbury Research Center Rhodia 259 Prospect Plains Road Cranbury NJ 08512 USA Abstract : When polyelectrolyte-neutral block copolymers are mixed in solutions to oppositely charged species (e.g. surfactant micelles, macromolecules, proteins etc…), there is the formation of stable “supermicellar” aggregates combining both components. The resulting colloidal complexes exhibit a core-shell structure and the mechanism yielding to their formation is electrostatic self-assembly. In this contribution, we report on the structural properties of “supermicellar” aggregates made from yttrium-based inorganic nanoparticles (radius 2 nm) and polyelectrolyte-neutral block copolymers in aqueous solutions. The yttrium hydroxyacetate particles were chosen as a model system for inorganic colloids, and also for their use in industrial applications as precursors for ceramic and opto-electronic materials. The copolymers placed under scrutiny are the water soluble and asymmetric poly(sodium acrylate)-b-poly(acrylamide) diblocks. Using static and dynamical light scattering experiments, we demonstrate the analogy between surfactant micelles and nanoparticles in the complexation phenomenon with oppositely charged polymers. We also determine the sizes and the aggregation numbers of the hybrid organic-inorganic 1 2 complexes. Several additional properties are discussed, such
    [Show full text]
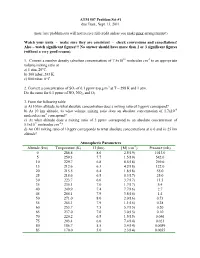
  • Problem Set #1 Due Tues., Sept
    ATM 507 Problem Set #1 due Tues., Sept. 13, 2011 (note: late problem sets will not receive full credit unless you make prior arrangements!) Watch your units - make sure they are consistent - check conversions and cancellations! Also – watch significant figures!!! No answer should have more than 2 or 3 significant figures (without a very good reason). 1. Convert a number density (absolute concentration) of 7.5x1012 molecules cm-3 to an appropriate volume mixing ratio at a) 1 atm, 20°C. b) 100 mbar, 243 K. c) 800 mbar, 0°C. -3 2. Convert a concentration of SO2 of 0.1 ppmv to μg m at T = 298 K and 1 atm. Do the same for 0.1 ppmv of NO, NO2, and O3. 3. From the following table a) At 10 km altitude, to what absolute concentration does a mixing ratio of 3 ppmv correspond? b) At 10 km altitude, to what volume mixing ratio does an absolute concentration of 1.7x1010 molecules cm-3 correspond? c) At what altitude does a mixing ratio of 3 ppmv correspond to an absolute concentration of 5.1x1011 molecules cm-3? d) An OH mixing ratio of 10 pptv corresponds to what absolute concentrations at i) 0 and ii) 25 km altitude? Atmospheric Parameters Altitude (km) Temperature (K) H (km) [M] (cm-3) Pressure (mb) 0 288.8 8.6 2.5(19) 1013.0 5 259.3 7.7 1.5(19) 542.0 10 229.7 6.8 8.5(18) 269.0 15 212.6 6.3 4.2(18) 122.0 20 215.5 6.4 1.8(18) 55.0 25 218.6 6.5 8.3(17) 25.0 30 223.7 6.6 3.7(17) 11.5 35 235.1 7.0 1.7(17) 5.4 40 249.9 7.4 7.7(16) 2.7 45 266.1 7.9 3.8(16) 1.4 50 271.0 8.0 2.0(16) 0.73 55 265.3 7.9 1.1(16) 0.38 60 253.7 7.5 5.7(15) 0.20 65 237.0 7.0 3.0(15) 0.10 70 220.2 6.5 1.5(15) 0.046 75 203.4 6.0 7.4(14) 0.021 80 186.7 5.5 3.4(14) 0.0089 85 170.0 5.0 2.3(14) 0.0055 4.
    [Show full text]
  • Redalyc.Calcite Dissolution by Mixing Waters: Geochemical Modeling And
    Geologica Acta: an international earth science journal ISSN: 1695-6133 [email protected] Universitat de Barcelona España SANZ, E.; AYORA, C.; CARRERA, J. Calcite dissolution by mixing waters: geochemical modeling and flow-through experiments Geologica Acta: an international earth science journal, vol. 9, núm. 1, marzo, 2011, pp. 67-77 Universitat de Barcelona Barcelona, España Available in: http://www.redalyc.org/articulo.oa?id=50522124007 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative Geologica Acta, Vol.9, Nº 1, March 2011, 67-77 DOI: 10.1344/105.000001652 Available online at www.geologica-acta.com Calcite dissolution by mixing waters: geochemical modeling and flow-through experiments 1 2 1 E. SANZ C. AYORA J. CARRERA 1 ExxonMobil Upstream Research Company Houston, Texas, USA E-mail: [email protected] 2 Institute of Enviromental Assessment and Water Research, IDAEA-ECSIC Barcelona, Spain ABSTRACT TABLE CAPTIONS Dissolution of carbonates has been commonly predicted by geochemical models to occur at the seawater-freshwater mixing zone of coastal aquifers along a geological time scale. However, field evidences are inconclusive:dissolution TABLE 1 Input end-member solutions used in the experiments and numerical simulations. Ω accounts for saturation, and I for ionic strength. vs. lack of dissolution. In this study we investigate the process of calcite dissolution by mixing waters of different salinities and pCO2, by means of geochemical modeling and laboratory experiments.
    [Show full text]
  • Mole Fraction - Wikipedia
    4/28/2020 Mole fraction - Wikipedia Mole fraction In chemistry, the mole fraction or molar fraction (xi) is defined as unit of the amount of a constituent (expressed in moles), ni divided by the total amount of all constituents in a mixture (also [1] expressed in moles), ntot: .These expression is given below:- The sum of all the mole fractions is equal to 1: The same concept expressed with a denominator of 100 is the mole percent or molar percentage or molar proportion (mol%). The mole fraction is also called the amount fraction.[1] It is identical to the number fraction, which is defined as the number of molecules of a constituent Ni divided by the total number of all molecules Ntot. The mole fraction is sometimes denoted by the lowercase Greek letter χ (chi) instead of a Roman x.[2][3] For mixtures of gases, IUPAC recommends the letter y.[1] The National Institute of Standards and Technology of the United States prefers the term amount-of- substance fraction over mole fraction because it does not contain the name of the unit mole.[4] Whereas mole fraction is a ratio of moles to moles, molar concentration is a quotient of moles to volume. The mole fraction is one way of expressing the composition of a mixture with a dimensionless quantity; mass fraction (percentage by weight, wt%) and volume fraction (percentage by volume, vol%) are others. Contents Properties Related quantities Mass fraction Molar mixing ratio Mixing binary mixtures with a common component to form ternary mixtures Mole percentage Mass concentration Molar concentration Mass and molar mass Spatial variation and gradient References https://en.wikipedia.org/wiki/Mole_fraction 1/5 4/28/2020 Mole fraction - Wikipedia Properties Mole fraction is used very frequently in the construction of phase diagrams.
    [Show full text]
  • 1 Atmospheric Sciences 501. Course Notes Autumn 1998. 1. Ideal Gas
    1 Atmospheric Sciences 501. Course Notes Autumn 1998. 1. Ideal Gas Law and Hydrostatics. 1.1 Ideal Gas Law. Basic thermodynamic variables are: Pressure, p (N m-2; 1 N m-2 = 1 pascal (Pa) = 0.01 millibar (mb) = 0.01hectoPascals (hPa). Density, r (kgm-3) Temperature, T (K) . If the energy due to intermolecular forces is small relative to molecular kinetic energy, the ideal gas law is an excellent approximation to the equation of state relating these variables: pRT=r (1.1) R* where R = = gas constant; R* = universal gas constant = 8314J kmol-1 K-1; M = molar M weight (kg/kg-mole) and R = specific gas constant for dry air = 287 J kg-1 K-1. 1.2 Molecules and the ideal gas law, Maxwell's kinetic interpretation. Note that r=nmÃà (1.2) where nà = number density (number of molecules per unit volume m-3), and mà = molecular mass (kg). Also MmA= à (1.3) where A = Avogadro's Number = 6.022x1026 molecules per mole; note that, since SI units are used, moles here are kilogram-moles, not gram-moles. Substituting (1.2) and (1.3) into (1.1): 2 æ R* ö p = ç ÷ nTÃÃ= knT (1.4) è A ø * æ R ö -23 -1 where k = ç ÷ = 1.381x10 J K is Boltzmann's Constant. è A ø Now consider the pressure exerted by molecules of gas on a surface perpendicular to the x- axis in a Cartesian reference frame. This is the force per unit area and is equivalent to the average flux in the x-direction of molecules with x-momentum mvà , mvÃà nv x ()xx× where () represents averaging over molecular velocities.
    [Show full text]
  • The Atmosphere
    The Atmosphere Atmospheric composition Measures of concentration Atmospheric pressure Barometric law Literature connected with today’s lecture: Jacob, chapter 1 - 2 Exercises: 1:1 – 1:6; 2:1 – 2:4 The Atmosphere The atmosphere –Thin “skin” of air surrounding the planet Description Role of natural atmosphere Effects of changed composition Atmospheric change Climate UV protection Acidification Health 1 Composition of the Atmosphere Dry atmosphere (excl. H2O): Gas Mixing ratio Dry atmosphere: (mole/mole) Dominated by nitrogen and oxygen Nitrogen (N2)0.78 Noble gases, in particular argon Oxygen (O2)0.21 Argon (Ar) 0.0093 Conc. (O2 + N2 + Ar) 1 mole/mole -6 Remaining components trace gases: E.g. Carbon dioxide (CO2) 365x10 Carbon dioxide, ozone, methane Neon (Ne) 18x10-6 -6 Ozone (O3) 0.01-10x10 Helium (He) 5.2x10-6 Humid atmosphere: -6 Water vapour: Varies, up to approx. 0.03 Methane (CH4) 1.7x10 moles/mole Krypton (Kr) 1.1x10-6 -9 Hydrogen (H2) 500x10 -9 Nitrous oxide (N2O) 320x10 Calculation Example: Calculate the density of dry air at T = 280 K and P = 1000 hPa! The atmosphere an ideal gas (in most cases): PV = nRT Density: = m/V = nM/V From the gas law: n/V = P/RT => =MP/RT Air is a mixture of gases – average molar mass: Ma = 29,0 kg/kmole Gas constant: R = 8314,3 J/(kmole K) Insert numbers: 3 = MaP/RT = 29,0*1000*100/(280*8314,3) = 1,25 kg/m 2 Atmospheric Concentration of Species Mixing ratio: Expressions atmospheric concentration: (No. moles of X)/(No. moles air molecules) Number concentration: Or: mass X/mass
    [Show full text]
  • Supplement of Tropospheric Sources and Sinks of Gas-Phase Acids in the Colorado Front Range
    Supplement of Atmos. Chem. Phys., 18, 12315–12327, 2018 https://doi.org/10.5194/acp-18-12315-2018-supplement © Author(s) 2018. This work is distributed under the Creative Commons Attribution 4.0 License. Supplement of Tropospheric sources and sinks of gas-phase acids in the Colorado Front Range James M. Mattila et al. Correspondence to: Delphine K. Farmer ([email protected]) The copyright of individual parts of the supplement might differ from the CC BY 4.0 License. Supplemental Figures Figure S1. Timeseries of tower elevator carriage altitude throughout the reported measurement period. Representative noon, night, and morning vertical profiles were measured at the periods denoted ‘A’, ‘B’, and ‘C’, respectively. Figure S2. Mixing ratio data timeseries for all detected gas-phase acids spanning the reported data acquisition period. All data were collected at 1 Hz acquisition rates. Figure S3. Vertical profiles of O3, NOx, CO, relative humidity, and air temperature at representative noon, night, and morning periods. Figure S4. Vertical profiles for all detected gas-phase acids at representative noon, night, and morning periods, showing mixing ratios as a function of altitude. Data are binned by altitude (10 m per bin). Data points are means of each bin. Error bars represent ± one standard deviation of binned values. Figure S5. Diel profile of NOx measured at the site throughout the reported measurement period. Data are binned by hour of day. Data points are binned means, and error bars are ± one standard deviation of binned data. Figure S6. Wind plot of ammonia measured at the BAO tower during the reported measurement period.
    [Show full text]