DOCSLIB.ORG

Transport and Scavenging of Soluble Gases in a Deep Convective Cloud

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Transport and Scavenging of Soluble Gases in a Deep Convective Cloud Transport and scavenging of soluble gases in a deep convective cloud The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Mari, Céline, Daniel J. Jacob, and Peter Bechtold. 2000. “Transport and Scavenging of Soluble Gases in a Deep Convective Cloud.” Journal of Geophysical Research 105 (D17): 22255. doi:10.1029/2000jd900211. Published Version doi:10.1029/2000JD900211 Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:14117823 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Other Posted Material, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#LAA JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 105, NO. D17, PAGES 22,255-22,267, SEPTEMBER 16, 2000 Transport and scavenging of soluble gases in a deep convective cloud Cdine Marl Laboratoired'A6rologie, UMR CNRS/Universit6Paul Sabatier,Toulouse, France Daniel J. Jacob Division of Engineeringand Applied Science,Harvard University, Cambridge, Massachusetts Peter Bechtold Laboratoire d'A6rologie,UMR CNRS/Universitd Paul Sabatier, Toulouse,France Abstract. A one-dimensionalentraining/detraining plume model is used to examine the transport and scavengingof soluble gasesin tropical deep convection. The model is applied to a continental system observedover Brazil during the Trace and AtmosphericChemistry Near the Equator-Atlantic (TRACE-A) TRACE-A aircraft campaign with outflows extending from 7 to 16 km altitude. Six gases are simulated: CO (inert tracer), CH3OOH, CH20, H202, HNO3 , and SO2. Observed(simulated) convective enhancement factors (CEF) at 7-12 km altitude, representingthe ratios of postconvectiveto preconvectivemixing ratios, are 2.4 (1.9) for CO, 11 (9.5) for CH3OOH, 2.9 (3.1) for CH20, 1.9 (1.2) for H202, and 0.8 (0.4) for HNO3. Simulated scavengingefficiencies in the convectivecolumn are 5% for CH3OOH, 23% for CH20, 66% for H202, 77% for HNO3, and 28% for SO2. The large CEF for CH3OOH reflects its low solubility and its boundary layer enrichment relative to the upper troposphere. The Henry's law constant for CH20 puts it at the threshold for etficient scavenging. Scavengingof SO2 is limited by the rate of aqueousphase reaction with H•O•, as H•O2 is itself efficiently scavengedby Henry's law equilibrium; efficient scavengingof SO2 requiresunusually high cloud water pH (pH > 6) to enablefast aqueousphase oxidation by Oa. Both HNO3 and HaOa are efficientlyscavenged in the lower (warm) part of the cloud, but H202 is released as the cloud freezes due to low retention efficiency during timing. Significant scavengingof H202 still takes place by cocondensationwith ice in the glaciated cloud but is less efficient than in the warm cloud. Inefficient scavengingof H202 in glaciated clouds may explain the observation,in TRACE-A and elsewhere, that HaO2 is enhanced in deep convective outflows while HNOa is depleted. Model results indicate little direct transfer of air from the boundary layer to the cloud anvil in the convective plume, because of low-level detrainment in the warm cloud and high-level entrainment in the glaciated cloud. We find instead a convectiveladder effect where midlevel outflow during the growing phase of the storm is teentrained into the convective plume as the storm matures. 1. Introduction thought due to the convectivetransport of radical pre- cursorssuch as acetone,peroxides and aldehydes[Sin#h Deep convection in the tropics is a critical mecha- et al., 1995; McKeen et al., 1997; Jae#l• et al., 1997; nisIn for transfer of air from the lower to the upper M•iller and Brasseur,1999]. Most of the NOx in the troposphere[Cotton et al., 1995]with many important upper troposphere is thought to originate from deep implicationsfor atmosphericchemistry [Prather and Ja- convective transport of NOx and nitrate reservoirs pro- cob,1997]. Recentstudies show that the upper tropo- ducedby surfacesources and lightning[Lamarque et al., sphere is more photochemically active than previously 1996; Jacob et al., 1996; Pickering et al., 1998; Jaegld et al., 19981. Deep convectivepumping of dimethyl- Copyright 2000 by the American GeophysicalUnion. sulfide and SO2 may drive efficient nucleation of sul- Paper number 2000JD900211. fate aerosolin convectiveoutflow [Chatfieldet Crutzen, 0148-0227/00/2000JD900211509.00 1984; Rodhe, 1999]. Considerableprecipitation takes 22,255 22,256 MARI ET AL.: TRANSPORT AND SCAVENGING OF SOLUBLE SPECIES place in associationwith deep convectionupdrafts, and an unresolved issue is the degree to which precipita- tion scavengingsuppresses the convectivecloud venting of water-solublegases [Andronache et al., 1999; Floss- mann and Wobrock,1996; Barth, 1994]. We present here an analysis of this issue. Our approachis based on a one-dimensional(l-D) entraining/detrainingplume model (P. Bechtoldet al., A mass flux convectionscheme for regional and global models, submitted to Quartely Journal of the Royal Meteorological Society, 2000; hereinafter Bechtold et al., submitted manuscript, 2000) that has been de- signedto providea deepconvective parameterization for mesoscaleand global-scalemodels. This model allows us to identify the key parameters controlling the ver- tical redistribution and scavengingof chemical species in a deep convectivecloud. We examine here the fate Grid cell of six different gasescovering a range of solubility in water: (1) CO as an insolubletracer of boundarylayer Figure 1. Schematicof the one-dimensionalconvec- pollution, (2) CH20, H20•, CH3OOH as precursorsfor tive cloud model with updraft and downdraft regions the HOx (HOx - OH + peroxy radicals)family in the (solidarrows), entrainment (open arrows with dashed uppertroposphere, (3) HNO3 as a reservoirfor NOx ? tails),detrainment (open arrows with dash-dottedtails) and (4) SO• as the precursorfor sulfateaerosols. and compensationallarge-scale subsidence (thick solid We focus our analysis on a tropical continental con- arrows) vective caseobserved during the Transport and Atmo- sphericChemistry Near the Equator-Atlantic(TRACE- A) aircraft experimentin September-October1992. dence and includes entrainment and detrainment pro- TRACE-A was designedto determine the role of biomass cesses(Figure 1). burning in causingthe large-scaleenhancement of tro- In the present application the model is initialized with posphericozone observed over the south Atlantic basin vertical profiles of temperature, water vapor and hori- in austral spring [Fishman et al., 1996]. Two flights zontal winds from the European Centre for Medium- over eastern Brazil examined the convective pumping Range Weather Forecasts(ECMWF) analysisat grid of biomass burning pollution to the upper troposphere. resolution 0.5 ø x 0.5ø. Convection is triggered by con- Of particular interest is flight 6, which provided vertical vective instability and large-scaleconvergence. The net profiles of gasesfor both preconvectiveand postconvec- convectiveavailable potential energy(CAPE) is usedto tive conditions[Pickering ct al., 1996]. We usethe data determine the updraft and downdraft air mass fluxes. from flight 6 to constrainand evaluate our simulationof At least 90% of the initial CAPE in the soundingmust convectivetransport and scavengingof chemicalspecies. be removed by the calculated convective fluxes. En- trainment and detrainment refer to mass exchangebe- tweenthe updraft and the environment(Figure 1). The 2. Model Description environment is defined as the grid scaleof the ECMWF 2.1. One-Dimensional Entraining/Detraining analysis and is also viewed here as the scale of the pre- convective aircraft observations. Plume Model Entrainment and detrainment rates are computed fol- A one-dimensional entraining/detraining plume lowingthe schemeof Kain and Fritsch[1990] as a func- model for wet convection(Bechtold et al., submitted tion of the buoyancy characteristicsof individual up- manuscript,2000) is usedfor this study. This modelhas draft subparcels. The mixing between clouds and their beendesigned to providea parameterizationof wet con- environments occurs very near the periphery of clouds vectionin the mesoscalemodel Meso-NH ILaroreet al., and generatessubparcels containing various proportions 1998].Subgrid-scale fluxes through convective updrafts of clear and cloudy air. Positively buoyant subparcels and mixing with the environmentthrough entrainment follow the cloudy updraft, entraining air from the en- and detrainment are diagnosedin terms of grid-scale vironment, while negatively buoyant subparcelsdetrain thermodynamicand dynamicvariables [Bechtold et al., to the environment. 2000;also Bechtold et al., submittedmanuscript, 2000]. At eachmodel level, the rate 5Mr (kgs-1), at which The formulation essentiallyfollows the schemeof Kain environmental air flows into the mixing region at the and Fritsch[1990] which is an advancedversion of the periphery of the updraft is expressedby Fritsch and Chappell[1980] scheme. The model pa- rameterizes a convectiveupdraft plume balanced by a convectivedowndraft plume and by large-scalesubsi- - 0.2 &, MARI ET AL.' TRANSPORT AND SCAVENGING OF SOLUBLE SPECIES 22,257 where R0 (1500 m) and Muo (kg s-•) are the updraft where C is the mixing ratio in the environmental air. radius and the massflux at cloud base, and 5z (m) is Entrainment is a critical process as it reduces the the vertical thickness of the level. The mass in this buoyancyof the cloudy air parcel and thus limits the mixing region
Load more

Recommended publications
  • Development Team
    Paper No: 16 Environmental Chemistry Module: 01 Environmental Concentration Units Development Team Prof. R.K. Kohli Principal Investigator & Prof. V.K. Garg & Prof. Ashok Dhawan Co- Principal Investigator Central University of Punjab, Bathinda Prof. K.S. Gupta Paper Coordinator University of Rajasthan, Jaipur Prof. K.S. Gupta Content Writer University of Rajasthan, Jaipur Content Reviewer Dr. V.K. Garg Central University of Punjab, Bathinda Anchor Institute Central University of Punjab 1 Environmental Chemistry Environmental Environmental Concentration Units Sciences Description of Module Subject Name Environmental Sciences Paper Name Environmental Chemistry Module Name/Title Environmental Concentration Units Module Id EVS/EC-XVI/01 Pre-requisites A basic knowledge of concentration units 1. To define exponents, prefixes and symbols based on SI units 2. To define molarity and molality 3. To define number density and mixing ratio 4. To define parts –per notation by volume Objectives 5. To define parts-per notation by mass by mass 6. To define mass by volume unit for trace gases in air 7. To define mass by volume unit for aqueous media 8. To convert one unit into another Keywords Environmental concentrations, parts- per notations, ppm, ppb, ppt, partial pressure 2 Environmental Chemistry Environmental Environmental Concentration Units Sciences Module 1: Environmental Concentration Units Contents 1. Introduction 2. Exponents 3. Environmental Concentration Units 4. Molarity, mol/L 5. Molality, mol/kg 6. Number Density (n) 7. Mixing Ratio 8. Parts-Per Notation by Volume 9. ppmv, ppbv and pptv 10. Parts-Per Notation by Mass by Mass. 11. Mass by Volume Unit for Trace Gases in Air: Microgram per Cubic Meter, µg/m3 12.
    [Show full text]
  • The Vertical Distribution of Soluble Gases in the Troposphere
    UC Irvine UC Irvine Previously Published Works Title The vertical distribution of soluble gases in the troposphere Permalink https://escholarship.org/uc/item/7gc9g430 Journal Geophysical Research Letters, 2(8) ISSN 0094-8276 Authors Stedman, DH Chameides, WL Cicerone, RJ Publication Date 1975 DOI 10.1029/GL002i008p00333 License https://creativecommons.org/licenses/by/4.0/ 4.0 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Vol. 2 No. 8 GEOPHYSICAL RESEARCHLETTERS August 1975 THE VERTICAL DISTRIBUTION OF SOLUBLE GASES IN THE TROPOSPHERE D. H. Stedman, W. L. Chameides, and R. J. Cicerone Space Physics Research Laboratory Department of Atmospheric and Oceanic Science The University of Michigan, Ann Arbor, Michigan 48105 Abstrg.ct. The thermodynamic properties of sev- Their arg:uments were based on the existence of an eral water-soluble gases are reviewed to determine HC1-H20 d•mer, but we consider the conclusions in- the likely effect of the atmospheric water cycle dependeht of the existence of dimers. For in- on their vertical profiles. We find that gaseous stance, Chameides[1975] has argued that HNO3 HC1, HN03, and HBr are sufficiently soluble in should follow the water-vapor mixing ratio gradi- water to suggest that their vertical profiles in ent, based on the high solubility of the gas in the troposphere have a similar shape to that of liquid water. In this work, we generalize the water va•or. Thuswe predict that HC1,HN03, and moredetailed argumentsof Chameides[1975] and HBr exhibit a steep negative gradient with alti- suggest which species should exhibit this nega- tude roughly equal to the altitude gradient of tive gradient and which should not.
    [Show full text]
  • Package 'Marelac'
    Package ‘marelac’ February 20, 2020 Version 2.1.10 Title Tools for Aquatic Sciences Author Karline Soetaert [aut, cre], Thomas Petzoldt [aut], Filip Meysman [cph], Lorenz Meire [cph] Maintainer Karline Soetaert <[email protected]> Depends R (>= 3.2), shape Imports stats, seacarb Description Datasets, constants, conversion factors, and utilities for 'MArine', 'Riverine', 'Estuarine', 'LAcustrine' and 'Coastal' science. The package contains among others: (1) chemical and physical constants and datasets, e.g. atomic weights, gas constants, the earths bathymetry; (2) conversion factors (e.g. gram to mol to liter, barometric units, temperature, salinity); (3) physical functions, e.g. to estimate concentrations of conservative substances, gas transfer and diffusion coefficients, the Coriolis force and gravity; (4) thermophysical properties of the seawater, as from the UNESCO polynomial or from the more recent derivation based on a Gibbs function. License GPL (>= 2) LazyData yes Repository CRAN Repository/R-Forge/Project marelac Repository/R-Forge/Revision 205 Repository/R-Forge/DateTimeStamp 2020-02-11 22:10:45 Date/Publication 2020-02-20 18:50:04 UTC NeedsCompilation yes 1 2 R topics documented: R topics documented: marelac-package . .3 air_density . .5 air_spechum . .6 atmComp . .7 AtomicWeight . .8 Bathymetry . .9 Constants . 10 convert_p . 11 convert_RtoS . 11 convert_salinity . 13 convert_StoCl . 15 convert_StoR . 16 convert_T . 17 coriolis . 18 diffcoeff . 19 earth_surf . 21 gas_O2sat . 23 gas_satconc . 25 gas_schmidt . 27 gas_solubility . 28 gas_transfer . 31 gravity . 33 molvol . 34 molweight . 36 Oceans . 37 redfield . 38 ssd2rad . 39 sw_adtgrad . 40 sw_alpha . 41 sw_beta . 42 sw_comp . 43 sw_conserv . 44 sw_cp . 45 sw_dens . 47 sw_depth . 49 sw_enthalpy . 50 sw_entropy . 51 sw_gibbs . 52 sw_kappa .
    [Show full text]
  • Calculation Exercises with Answers and Solutions
    Atmospheric Chemistry and Physics Calculation Exercises Contents Exercise A, chapter 1 - 3 in Jacob …………………………………………………… 2 Exercise B, chapter 4, 6 in Jacob …………………………………………………… 6 Exercise C, chapter 7, 8 in Jacob, OH on aerosols and booklet by Heintzenberg … 11 Exercise D, chapter 9 in Jacob………………………………………………………. 16 Exercise E, chapter 10 in Jacob……………………………………………………… 20 Exercise F, chapter 11 - 13 in Jacob………………………………………………… 24 Answers and solutions …………………………………………………………………. 29 Note that approximately 40% of the written exam deals with calculations. The remainder is about understanding of the theory. Exercises marked with an asterisk (*) are for the most interested students. These exercises are more comprehensive and/or difficult than questions appearing in the written exam. 1 Atmospheric Chemistry and Physics – Exercise A, chap. 1 – 3 Recommended activity before exercise: Try to solve 1:1 – 1:5, 2:1 – 2:2 and 3:1 – 3:2. Summary: Concentration Example Advantage Number density No. molecules/m3, Useful for calculations of reaction kmol/m3 rates in the gas phase Partial pressure Useful measure on the amount of a substance that easily can be converted to mixing ratio Mixing ratio ppmv can mean e.g. Concentration relative to the mole/mole or partial concentration of air molecules. Very pressure/total pressure useful because air is compressible. Ideal gas law: PV = nRT Molar mass: M = m/n Density: ρ = m/V = PM/RT; (from the two equations above) Mixing ratio (vol): Cx = nx/na = Px/Pa ≠ mx/ma Number density: Cvol = nNav/V 26 -1 Avogadro’s
    [Show full text]
  • Lecture 3. the Basic Properties of the Natural Atmosphere 1. Composition
    Lecture 3. The basic properties of the natural atmosphere Objectives: 1. Composition of air. 2. Pressure. 3. Temperature. 4. Density. 5. Concentration. Mole. Mixing ratio. 6. Gas laws. 7. Dry air and moist air. Readings: Turco: p.11-27, 38-43, 366-367, 490-492; Brimblecombe: p. 1-5 1. Composition of air. The word atmosphere derives from the Greek atmo (vapor) and spherios (sphere). The Earth’s atmosphere is a mixture of gases that we call air. Air usually contains a number of small particles (atmospheric aerosols), clouds of condensed water, and ice cloud. NOTE : The atmosphere is a thin veil of gases; if our planet were the size of an apple, its atmosphere would be thick as the apple peel. Some 80% of the mass of the atmosphere is within 10 km of the surface of the Earth, which has a diameter of about 12,742 km. The Earth’s atmosphere as a mixture of gases is characterized by pressure, temperature, and density which vary with altitude (will be discussed in Lecture 4). The atmosphere below about 100 km is called Homosphere. This part of the atmosphere consists of uniform mixtures of gases as illustrated in Table 3.1. 1 Table 3.1. The composition of air. Gases Fraction of air Constant gases Nitrogen, N2 78.08% Oxygen, O2 20.95% Argon, Ar 0.93% Neon, Ne 0.0018% Helium, He 0.0005% Krypton, Kr 0.00011% Xenon, Xe 0.000009% Variable gases Water vapor, H2O 4.0% (maximum, in the tropics) 0.00001% (minimum, at the South Pole) Carbon dioxide, CO2 0.0365% (increasing ~0.4% per year) Methane, CH4 ~0.00018% (increases due to agriculture) Hydrogen, H2 ~0.00006% Nitrous oxide, N2O ~0.00003% Carbon monoxide, CO ~0.000009% Ozone, O3 ~0.000001% - 0.0004% Fluorocarbon 12, CF2Cl2 ~0.00000005% Other gases 1% Oxygen 21% Nitrogen 78% 2 • Some gases in Table 3.1 are called constant gases because the ratio of the number of molecules for each gas and the total number of molecules of air do not change substantially from time to time or place to place.
    [Show full text]
  • Interactions Between Polymers and Nanoparticles : Formation of « Supermicellar » Hybrid Aggregates
    1 Interactions between Polymers and Nanoparticles : Formation of « Supermicellar » Hybrid Aggregates J.-F. Berret@, K. Yokota* and M. Morvan, Complex Fluids Laboratory, UMR CNRS - Rhodia n°166, Cranbury Research Center Rhodia 259 Prospect Plains Road Cranbury NJ 08512 USA Abstract : When polyelectrolyte-neutral block copolymers are mixed in solutions to oppositely charged species (e.g. surfactant micelles, macromolecules, proteins etc…), there is the formation of stable “supermicellar” aggregates combining both components. The resulting colloidal complexes exhibit a core-shell structure and the mechanism yielding to their formation is electrostatic self-assembly. In this contribution, we report on the structural properties of “supermicellar” aggregates made from yttrium-based inorganic nanoparticles (radius 2 nm) and polyelectrolyte-neutral block copolymers in aqueous solutions. The yttrium hydroxyacetate particles were chosen as a model system for inorganic colloids, and also for their use in industrial applications as precursors for ceramic and opto-electronic materials. The copolymers placed under scrutiny are the water soluble and asymmetric poly(sodium acrylate)-b-poly(acrylamide) diblocks. Using static and dynamical light scattering experiments, we demonstrate the analogy between surfactant micelles and nanoparticles in the complexation phenomenon with oppositely charged polymers. We also determine the sizes and the aggregation numbers of the hybrid organic-inorganic 1 2 complexes. Several additional properties are discussed, such
    [Show full text]
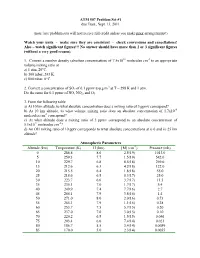
  • Problem Set #1 Due Tues., Sept
    ATM 507 Problem Set #1 due Tues., Sept. 13, 2011 (note: late problem sets will not receive full credit unless you make prior arrangements!) Watch your units - make sure they are consistent - check conversions and cancellations! Also – watch significant figures!!! No answer should have more than 2 or 3 significant figures (without a very good reason). 1. Convert a number density (absolute concentration) of 7.5x1012 molecules cm-3 to an appropriate volume mixing ratio at a) 1 atm, 20°C. b) 100 mbar, 243 K. c) 800 mbar, 0°C. -3 2. Convert a concentration of SO2 of 0.1 ppmv to μg m at T = 298 K and 1 atm. Do the same for 0.1 ppmv of NO, NO2, and O3. 3. From the following table a) At 10 km altitude, to what absolute concentration does a mixing ratio of 3 ppmv correspond? b) At 10 km altitude, to what volume mixing ratio does an absolute concentration of 1.7x1010 molecules cm-3 correspond? c) At what altitude does a mixing ratio of 3 ppmv correspond to an absolute concentration of 5.1x1011 molecules cm-3? d) An OH mixing ratio of 10 pptv corresponds to what absolute concentrations at i) 0 and ii) 25 km altitude? Atmospheric Parameters Altitude (km) Temperature (K) H (km) [M] (cm-3) Pressure (mb) 0 288.8 8.6 2.5(19) 1013.0 5 259.3 7.7 1.5(19) 542.0 10 229.7 6.8 8.5(18) 269.0 15 212.6 6.3 4.2(18) 122.0 20 215.5 6.4 1.8(18) 55.0 25 218.6 6.5 8.3(17) 25.0 30 223.7 6.6 3.7(17) 11.5 35 235.1 7.0 1.7(17) 5.4 40 249.9 7.4 7.7(16) 2.7 45 266.1 7.9 3.8(16) 1.4 50 271.0 8.0 2.0(16) 0.73 55 265.3 7.9 1.1(16) 0.38 60 253.7 7.5 5.7(15) 0.20 65 237.0 7.0 3.0(15) 0.10 70 220.2 6.5 1.5(15) 0.046 75 203.4 6.0 7.4(14) 0.021 80 186.7 5.5 3.4(14) 0.0089 85 170.0 5.0 2.3(14) 0.0055 4.
    [Show full text]
  • Redalyc.Calcite Dissolution by Mixing Waters: Geochemical Modeling And
    Geologica Acta: an international earth science journal ISSN: 1695-6133 [email protected] Universitat de Barcelona España SANZ, E.; AYORA, C.; CARRERA, J. Calcite dissolution by mixing waters: geochemical modeling and flow-through experiments Geologica Acta: an international earth science journal, vol. 9, núm. 1, marzo, 2011, pp. 67-77 Universitat de Barcelona Barcelona, España Available in: http://www.redalyc.org/articulo.oa?id=50522124007 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative Geologica Acta, Vol.9, Nº 1, March 2011, 67-77 DOI: 10.1344/105.000001652 Available online at www.geologica-acta.com Calcite dissolution by mixing waters: geochemical modeling and flow-through experiments 1 2 1 E. SANZ C. AYORA J. CARRERA 1 ExxonMobil Upstream Research Company Houston, Texas, USA E-mail: [email protected] 2 Institute of Enviromental Assessment and Water Research, IDAEA-ECSIC Barcelona, Spain ABSTRACT TABLE CAPTIONS Dissolution of carbonates has been commonly predicted by geochemical models to occur at the seawater-freshwater mixing zone of coastal aquifers along a geological time scale. However, field evidences are inconclusive:dissolution TABLE 1 Input end-member solutions used in the experiments and numerical simulations. Ω accounts for saturation, and I for ionic strength. vs. lack of dissolution. In this study we investigate the process of calcite dissolution by mixing waters of different salinities and pCO2, by means of geochemical modeling and laboratory experiments.
    [Show full text]
  • Mole Fraction - Wikipedia
    4/28/2020 Mole fraction - Wikipedia Mole fraction In chemistry, the mole fraction or molar fraction (xi) is defined as unit of the amount of a constituent (expressed in moles), ni divided by the total amount of all constituents in a mixture (also [1] expressed in moles), ntot: .These expression is given below:- The sum of all the mole fractions is equal to 1: The same concept expressed with a denominator of 100 is the mole percent or molar percentage or molar proportion (mol%). The mole fraction is also called the amount fraction.[1] It is identical to the number fraction, which is defined as the number of molecules of a constituent Ni divided by the total number of all molecules Ntot. The mole fraction is sometimes denoted by the lowercase Greek letter χ (chi) instead of a Roman x.[2][3] For mixtures of gases, IUPAC recommends the letter y.[1] The National Institute of Standards and Technology of the United States prefers the term amount-of- substance fraction over mole fraction because it does not contain the name of the unit mole.[4] Whereas mole fraction is a ratio of moles to moles, molar concentration is a quotient of moles to volume. The mole fraction is one way of expressing the composition of a mixture with a dimensionless quantity; mass fraction (percentage by weight, wt%) and volume fraction (percentage by volume, vol%) are others. Contents Properties Related quantities Mass fraction Molar mixing ratio Mixing binary mixtures with a common component to form ternary mixtures Mole percentage Mass concentration Molar concentration Mass and molar mass Spatial variation and gradient References https://en.wikipedia.org/wiki/Mole_fraction 1/5 4/28/2020 Mole fraction - Wikipedia Properties Mole fraction is used very frequently in the construction of phase diagrams.
    [Show full text]
  • 1 Atmospheric Sciences 501. Course Notes Autumn 1998. 1. Ideal Gas
    1 Atmospheric Sciences 501. Course Notes Autumn 1998. 1. Ideal Gas Law and Hydrostatics. 1.1 Ideal Gas Law. Basic thermodynamic variables are: Pressure, p (N m-2; 1 N m-2 = 1 pascal (Pa) = 0.01 millibar (mb) = 0.01hectoPascals (hPa). Density, r (kgm-3) Temperature, T (K) . If the energy due to intermolecular forces is small relative to molecular kinetic energy, the ideal gas law is an excellent approximation to the equation of state relating these variables: pRT=r (1.1) R* where R = = gas constant; R* = universal gas constant = 8314J kmol-1 K-1; M = molar M weight (kg/kg-mole) and R = specific gas constant for dry air = 287 J kg-1 K-1. 1.2 Molecules and the ideal gas law, Maxwell's kinetic interpretation. Note that r=nmÃà (1.2) where nà = number density (number of molecules per unit volume m-3), and mà = molecular mass (kg). Also MmA= à (1.3) where A = Avogadro's Number = 6.022x1026 molecules per mole; note that, since SI units are used, moles here are kilogram-moles, not gram-moles. Substituting (1.2) and (1.3) into (1.1): 2 æ R* ö p = ç ÷ nTÃÃ= knT (1.4) è A ø * æ R ö -23 -1 where k = ç ÷ = 1.381x10 J K is Boltzmann's Constant. è A ø Now consider the pressure exerted by molecules of gas on a surface perpendicular to the x- axis in a Cartesian reference frame. This is the force per unit area and is equivalent to the average flux in the x-direction of molecules with x-momentum mvà , mvÃà nv x ()xx× where () represents averaging over molecular velocities.
    [Show full text]
  • The Atmosphere
    The Atmosphere Atmospheric composition Measures of concentration Atmospheric pressure Barometric law Literature connected with today’s lecture: Jacob, chapter 1 - 2 Exercises: 1:1 – 1:6; 2:1 – 2:4 The Atmosphere The atmosphere –Thin “skin” of air surrounding the planet Description Role of natural atmosphere Effects of changed composition Atmospheric change Climate UV protection Acidification Health 1 Composition of the Atmosphere Dry atmosphere (excl. H2O): Gas Mixing ratio Dry atmosphere: (mole/mole) Dominated by nitrogen and oxygen Nitrogen (N2)0.78 Noble gases, in particular argon Oxygen (O2)0.21 Argon (Ar) 0.0093 Conc. (O2 + N2 + Ar) 1 mole/mole -6 Remaining components trace gases: E.g. Carbon dioxide (CO2) 365x10 Carbon dioxide, ozone, methane Neon (Ne) 18x10-6 -6 Ozone (O3) 0.01-10x10 Helium (He) 5.2x10-6 Humid atmosphere: -6 Water vapour: Varies, up to approx. 0.03 Methane (CH4) 1.7x10 moles/mole Krypton (Kr) 1.1x10-6 -9 Hydrogen (H2) 500x10 -9 Nitrous oxide (N2O) 320x10 Calculation Example: Calculate the density of dry air at T = 280 K and P = 1000 hPa! The atmosphere an ideal gas (in most cases): PV = nRT Density: = m/V = nM/V From the gas law: n/V = P/RT => =MP/RT Air is a mixture of gases – average molar mass: Ma = 29,0 kg/kmole Gas constant: R = 8314,3 J/(kmole K) Insert numbers: 3 = MaP/RT = 29,0*1000*100/(280*8314,3) = 1,25 kg/m 2 Atmospheric Concentration of Species Mixing ratio: Expressions atmospheric concentration: (No. moles of X)/(No. moles air molecules) Number concentration: Or: mass X/mass
    [Show full text]
  • Supplement of Tropospheric Sources and Sinks of Gas-Phase Acids in the Colorado Front Range
    Supplement of Atmos. Chem. Phys., 18, 12315–12327, 2018 https://doi.org/10.5194/acp-18-12315-2018-supplement © Author(s) 2018. This work is distributed under the Creative Commons Attribution 4.0 License. Supplement of Tropospheric sources and sinks of gas-phase acids in the Colorado Front Range James M. Mattila et al. Correspondence to: Delphine K. Farmer ([email protected]) The copyright of individual parts of the supplement might differ from the CC BY 4.0 License. Supplemental Figures Figure S1. Timeseries of tower elevator carriage altitude throughout the reported measurement period. Representative noon, night, and morning vertical profiles were measured at the periods denoted ‘A’, ‘B’, and ‘C’, respectively. Figure S2. Mixing ratio data timeseries for all detected gas-phase acids spanning the reported data acquisition period. All data were collected at 1 Hz acquisition rates. Figure S3. Vertical profiles of O3, NOx, CO, relative humidity, and air temperature at representative noon, night, and morning periods. Figure S4. Vertical profiles for all detected gas-phase acids at representative noon, night, and morning periods, showing mixing ratios as a function of altitude. Data are binned by altitude (10 m per bin). Data points are means of each bin. Error bars represent ± one standard deviation of binned values. Figure S5. Diel profile of NOx measured at the site throughout the reported measurement period. Data are binned by hour of day. Data points are binned means, and error bars are ± one standard deviation of binned data. Figure S6. Wind plot of ammonia measured at the BAO tower during the reported measurement period.
    [Show full text]