DOCSLIB.ORG

Development Team

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Development Team Paper No: 16 Environmental Chemistry Module: 01 Environmental Concentration Units Development Team Prof. R.K. Kohli Principal Investigator & Prof. V.K. Garg & Prof. Ashok Dhawan Co- Principal Investigator Central University of Punjab, Bathinda Prof. K.S. Gupta Paper Coordinator University of Rajasthan, Jaipur Prof. K.S. Gupta Content Writer University of Rajasthan, Jaipur Content Reviewer Dr. V.K. Garg Central University of Punjab, Bathinda Anchor Institute Central University of Punjab 1 Environmental Chemistry Environmental Environmental Concentration Units Sciences Description of Module Subject Name Environmental Sciences Paper Name Environmental Chemistry Module Name/Title Environmental Concentration Units Module Id EVS/EC-XVI/01 Pre-requisites A basic knowledge of concentration units 1. To define exponents, prefixes and symbols based on SI units 2. To define molarity and molality 3. To define number density and mixing ratio 4. To define parts –per notation by volume Objectives 5. To define parts-per notation by mass by mass 6. To define mass by volume unit for trace gases in air 7. To define mass by volume unit for aqueous media 8. To convert one unit into another Keywords Environmental concentrations, parts- per notations, ppm, ppb, ppt, partial pressure 2 Environmental Chemistry Environmental Environmental Concentration Units Sciences Module 1: Environmental Concentration Units Contents 1. Introduction 2. Exponents 3. Environmental Concentration Units 4. Molarity, mol/L 5. Molality, mol/kg 6. Number Density (n) 7. Mixing Ratio 8. Parts-Per Notation by Volume 9. ppmv, ppbv and pptv 10. Parts-Per Notation by Mass by Mass. 11. Mass by Volume Unit for Trace Gases in Air: Microgram per Cubic Meter, µg/m3 12. Conversion from µg m-3 to ppbv 13. Mass by Volume Unit for Aqueous Media: mg per liter or ppm 14. Conversion from One Unit to Another 15. Pressure, Partial Pressure and Units 16. Suggesting Reading Introduction A large number of chemical species are found in the environment. To express their amounts, it is necessary to specify the unit of measurement. In general, SI units (Système international d'unités) are used, although some other units may also be found occasionally. SI unit for length is meter, m, for mass is kilogram, kg, and for time is second, s. These basic units are utilized to obtain derived units for 3 Environmental Chemistry Environmental Environmental Concentration Units Sciences physical parameters. It must be pointed out that environmental chemistry is concerned mainly with air and aquatic chemistry and therefore the discussion on units is concerned mainly with these systems. Exponents The amounts of different substances present in environment differ by several orders of magnitude, say from 0.00000001 to 1,00,00,00,000, i. e., from 1x10-8 to 1x 108. For the sake of brevity, ease in writing and to avoid writing several zeros, the exponents, as given in Table 1, are used. One may come across the use of billion, million etc., hence following equalities may be remembered: tera = trillion; giga = billion; mega = million; kilo = thousand, hecto = hundred and deca = ten. Environmental chemistry deals mainly with trace amounts of contaminants and pollutants in air and aqueous systems, therefore, the entire discussion is based on this... Table 1. Exponents, prefixes and symbols based on SI units. Multiple Prefix Symbol Multiple Prefix Symbol 1012 tera T 10-2 centi c 109 giga G 10-3 milli m 106 mega M 10-6 micro µ 103 kilo k 10-9 nano n 102 hecto h 10-12 pico p 10 deca da 10-15 femto f 10-1 deci d 10-18 atto a 4 Environmental Chemistry Environmental Environmental Concentration Units Sciences Environmental Concentration Units The concentrations of the gaseous substances can be expressed using absolute and relative scales. An example of the former are molarity, molality and number density and of the latter are mixing ratio and mole fraction. Molarity, mol/L The most preferred unit of expressing concentrations of the substances in chemistry is molarity. It is defined as the number of moles of a solute dissolved in one liter of the solution. Its unit is mol/L or mol L-1. It is defined by Eq. 1. molarity = mass of solute in g/(M. W. of solute × volume of solution in L) (1) Problem 1.. A 100 mL solution was prepared by dissolving 0.5845 g NaCl (M. W. = 58.45 g/mol) in water. Calculate molarity of NaCl. Solution. Convert volume100 mL in to 0.1 L and then the molarity of NaCl using Eq. 1. is: molarity of NaCl = 0.5845 g/58.45 g mol-1x 100 mL = 0.5845 g/ 58.45 g mol-1x 0.1L = 0.1 mol L-1. Molality, mol/kg It is defined as the number of moles of a solute dissolved in one kg of the solvent. Its unit is mol/kg as in Eq 2. molality = mass of solute in g/(M. W. x mass of solvent in kg) (2) It does not depend on temperature. 5 Environmental Chemistry Environmental Environmental Concentration Units Sciences Problem 2. For preparing 0.01 molal solution of NaCl, how many grams of NaCl should be dissolved in 500 g of water? Solution. After converting 500 g of water in to 0.5 kg, use Eq. 2 as follows: 0.01 mol kg-1= mass of NaCl in g /(58.45 g mol-1 x 0.5 kg) mass of NaCl = 0.01 mol kg-1x 58.45 g mol -1x 0.5 kg = 0.29225 g Number Density (n) The number density, n, is defined as the number of molecules per unit volume as in Eq. 1. nx = total number of molecules of X / total volume of air (3) where nx is the number density of gaseous substance X. The unit of number density is molecules /cm3 or molecules cm-3. Number density is widely used in measuring reaction rates and optical properties of atmosphere. While reporting number density, it is necessary to report environmental conditions such as temperature and pressure because the value of volume depends on these parameters and so the number density will also depend on these parameters. -6 6 Problem 3. Then number of CO2 molecules in 4 x 10 L air is 2x10 . Calculate the number density of CO2. Solution. The number density, nCO2, can be calculated as follows: 6 Environmental Chemistry Environmental Environmental Concentration Units Sciences nCO2 = total number of molecules of CO2/Total volume of air. 6 -6 nCO2 = 2x10 / 4 x 10 11 3 nCO2 = 5 x10 molecules/ cm Mixing Ratio Mixing ratio, Cx, is equal to the number of moles per mole of air as in Eq. 2. Cx = total number of moles of X/ total number of moles of air (4) The mixing ratio is a dimensionless quantity because the amounts of X and air are in the same unit of mole, which cancels out. The environmental science, in general, deals with trace amounts of pollutants in gas phase and with trace impurities in aqueous systems. It is, therefore, preferred to express the concentrations of trace substances in the form of parts-per notation, which can be expressed as volume by volume (V/V) or mass by mass (m/m). ppm, ppb and ppt are calculated in volume-per-volume ratio and so the correct representation is ppmv, ppbv and pptv. In an environment if the amount CO be 1 ppmv, it means 1mL of CO is present in 1 million mL of air. Parts-Per Notation by Volume The concentrations of gaseous substances in air determined as volume by volume ratio should be expressed as parts per million by volume (ppmv), parts per billion by volume (ppbv) and parts per trillion by volume (pptv). Unfortunately, most often ‘v’ is dropped and the values are written as ppm, ppb and ppt. 7 Environmental Chemistry Environmental Environmental Concentration Units Sciences ppmv, ppbv and pptv One ppm means one unit volume of the trace substance to be present in one million volume. For example if in air reported CO be 2 ppmv, it means 2mL CO is present in one million mL of air, or 2mL CO is present in one m3 of air. ppbv and pptv have similar meaning. According to parts-per notation the values of ppmv, ppbv and pptv can be expressed as in Eqs.5-7. 푛푢푚푏푒푟 표푓 푝푎푟푡푠 표푓 푎 표푛푠푡푡푢푒푛푡 푝푝푚푣 = ×106 (5) 푡표푡푎푙 푛푢푚푏푒푟 표푓 푝푎푟푡푠 표푓 푎푙푙 푡ℎ푒 푐표푛푠푡푡푢푒푛푡푠 푛푢푚푏푒푟 표푓 푝푎푟푡푠 표푓 푎 푐표푛푠푡푡푢푒푛푡 푝푝푏푣 = ×109 (6) 푡표푡푎푙 푛푢푚푏푒푟 표푓 푝푎푟푡푠 표푓 푎푙푙푡ℎ푒 푐표푛푠푡푡푢푒푛푡푠 푛푢푚푏푒푟 표푓 푝푎푟푡푠 표푓 푎 푐표푛푠푡푡푢푒푛푡 푝푝푡푣 = ×1012 (7) 푡표푡푎푙 푛푢푚푏푒푟 표푓 푝푎푟푡푠 표푓 푎푙푙 푡ℎ푒 푐표푛푠푡푡푢푒푛푡푠 The quantities in numerator and denominator must be in the same unit and hence values of ppmv, ppbv and pptv are dimensionless. The amounts of the components are expressed in several units, which all are proportional to number of moles, for example: number of moles of a gaseous constituent are proportional to its volume, number of molecules of a gaseous constituent are proportional to number of its moles and number of moles of a gaseous constituent are proportional to its partial pressure Based on these considerations, the formulas in Eq. 5 become: 8 Environmental Chemistry Environmental Environmental Concentration Units Sciences 푛푢푚푏푒푟 표푓 푚표푙푒푠 표푓 푎 푐표푛푠푡푡푢푒푛푡 푝푝푚푣 = ×106 (8) 푡표푡푎푙 푛푢푚푏푒푟 표푓 푚표푙푒푠 표푓 푎푙푙 푡ℎ푒 푐표푛푠푡푡푢푒푛푡푠 푣표푙푢푚푒 표푓 푎 푐표푛푠푡푡푢푒푛푡 푝푝푚푣 = ×106 (9) 푡표푡푎푙 푣표푙푢푚푒 표푓 푝푎푟푡푠 표푓 푎푙푙 푡ℎ푒 푐표푛푠푡푡푢푒푛푡푠 푛푢푚푏푒푟 표푓 푚표푙푒푐푢푙푒푠 표푓 푎 푐표푛푠푡푡푢푒푛푡 푝푝푚푣 = ×106 (10) 푡표푡푎푙 푛푢푚푏푒푟 표푓 푚표푙푒푐푢푙푒푠 표푓 푎푙푙 푡ℎ푒 푐표푛푠푡푡푢푒푛푡푠 푝푎푟푡푎푙 푝푟푒푠푠푢푟푒 표푓 푎 푐표푛푠푡푡푢푒푛푡 푝푝푚푣 = ×106 (11) 푡표푡푎푙 푝푟푒푠푠푢푟푒 표푓 푝푎푟푡푠 표푓 푎푙푙 푡ℎ푒 푐표푛푠푡푡푢푒푛푡푠 Likewise, the equations for ppbv and pptv can be written based on Eqs.
Load more

Recommended publications
  • Supplement Of
    Supplement of Effects of Liquid–Liquid Phase Separation and Relative Humidity on the Heterogeneous OH Oxidation of Inorganic-Organic Aerosols: Insights from Methylglutaric Acid/Ammonium Sulfate Particles Hoi Ki Lam1, Rongshuang Xu1, Jack Choczynski2, James F. Davies2, Dongwan Ham3, Mijung Song3, Andreas Zuend4, Wentao Li5, Ying-Lung Steve Tse5, Man Nin Chan 1,6 1Earth System Science Programme, Faculty of Science, The Chinese University of Hong Kong, Hong Kong, China 2Department of Chemistry, University of California Riverside, Riverside, CA, USA 3Department of Earth and Environmental Sciences, Jeonbuk National University, Jeollabuk-do, Republic of Korea 4Department of Atmospheric and Oceanic Sciences, McGill University, Montreal, Québec, Canada 5Departemnt of Chemistry, The Chinese University of Hong Kong, Hong Kong, China’ 6The Institute of Environment, Energy and Sustainability, The Chinese University of Hong Kong, Hong Kong, China Corresponding author: [email protected] Table S1. Composition, viscosity, diffusion coefficient and mixing time scale of aqueous droplets containing 3-MGA and ammonium sulfate (AS) in an organic- to-inorganic dry mass ratio (OIR) = 1 at different RH predicted by the AIOMFAC-LLE. RH (%) 55 60 65 70 75 80 85 88 Salt-rich phase (Phase α) Mass fraction of 3-MGA 0.00132 0.00372 0.00904 0.0202 / / Mass fraction of AS 0.658 0.616 0.569 0.514 / / Mass fraction of H2O 0.341 0.380 0.422 0.466 / / Organic-rich phase (Phase β) Mass fraction of 3-MGA 0.612 0.596 0.574 0.546 / / Mass fraction of AS 0.218 0.209 0.199 0.190
    [Show full text]
  • Colloidal Suspensions
    Chapter 9 Colloidal suspensions 9.1 Introduction So far we have discussed the motion of one single Brownian particle in a surrounding fluid and eventually in an extaernal potential. There are many practical applications of colloidal suspensions where several interacting Brownian particles are dissolved in a fluid. Colloid science has a long history startying with the observations by Robert Brown in 1828. The colloidal state was identified by Thomas Graham in 1861. In the first decade of last century studies of colloids played a central role in the development of statistical physics. The experiments of Perrin 1910, combined with Einstein's theory of Brownian motion from 1905, not only provided a determination of Avogadro's number but also laid to rest remaining doubts about the molecular composition of matter. An important event in the development of a quantitative description of colloidal systems was the derivation of effective pair potentials of charged colloidal particles. Much subsequent work, largely in the domain of chemistry, dealt with the stability of charged colloids and their aggregation under the influence of van der Waals attractions when the Coulombic repulsion is screened strongly by the addition of electrolyte. Synthetic colloidal spheres were first made in the 1940's. In the last twenty years the availability of several such reasonably well characterised "model" colloidal systems has attracted physicists to the field once more. The study, both theoretical and experimental, of the structure and dynamics of colloidal suspensions is now a vigorous and growing subject which spans chemistry, chemical engineering and physics. A colloidal dispersion is a heterogeneous system in which particles of solid or droplets of liquid are dispersed in a liquid medium.
    [Show full text]
  • The Vertical Distribution of Soluble Gases in the Troposphere
    UC Irvine UC Irvine Previously Published Works Title The vertical distribution of soluble gases in the troposphere Permalink https://escholarship.org/uc/item/7gc9g430 Journal Geophysical Research Letters, 2(8) ISSN 0094-8276 Authors Stedman, DH Chameides, WL Cicerone, RJ Publication Date 1975 DOI 10.1029/GL002i008p00333 License https://creativecommons.org/licenses/by/4.0/ 4.0 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Vol. 2 No. 8 GEOPHYSICAL RESEARCHLETTERS August 1975 THE VERTICAL DISTRIBUTION OF SOLUBLE GASES IN THE TROPOSPHERE D. H. Stedman, W. L. Chameides, and R. J. Cicerone Space Physics Research Laboratory Department of Atmospheric and Oceanic Science The University of Michigan, Ann Arbor, Michigan 48105 Abstrg.ct. The thermodynamic properties of sev- Their arg:uments were based on the existence of an eral water-soluble gases are reviewed to determine HC1-H20 d•mer, but we consider the conclusions in- the likely effect of the atmospheric water cycle dependeht of the existence of dimers. For in- on their vertical profiles. We find that gaseous stance, Chameides[1975] has argued that HNO3 HC1, HN03, and HBr are sufficiently soluble in should follow the water-vapor mixing ratio gradi- water to suggest that their vertical profiles in ent, based on the high solubility of the gas in the troposphere have a similar shape to that of liquid water. In this work, we generalize the water va•or. Thuswe predict that HC1,HN03, and moredetailed argumentsof Chameides[1975] and HBr exhibit a steep negative gradient with alti- suggest which species should exhibit this nega- tude roughly equal to the altitude gradient of tive gradient and which should not.
    [Show full text]
  • Package 'Marelac'
    Package ‘marelac’ February 20, 2020 Version 2.1.10 Title Tools for Aquatic Sciences Author Karline Soetaert [aut, cre], Thomas Petzoldt [aut], Filip Meysman [cph], Lorenz Meire [cph] Maintainer Karline Soetaert <[email protected]> Depends R (>= 3.2), shape Imports stats, seacarb Description Datasets, constants, conversion factors, and utilities for 'MArine', 'Riverine', 'Estuarine', 'LAcustrine' and 'Coastal' science. The package contains among others: (1) chemical and physical constants and datasets, e.g. atomic weights, gas constants, the earths bathymetry; (2) conversion factors (e.g. gram to mol to liter, barometric units, temperature, salinity); (3) physical functions, e.g. to estimate concentrations of conservative substances, gas transfer and diffusion coefficients, the Coriolis force and gravity; (4) thermophysical properties of the seawater, as from the UNESCO polynomial or from the more recent derivation based on a Gibbs function. License GPL (>= 2) LazyData yes Repository CRAN Repository/R-Forge/Project marelac Repository/R-Forge/Revision 205 Repository/R-Forge/DateTimeStamp 2020-02-11 22:10:45 Date/Publication 2020-02-20 18:50:04 UTC NeedsCompilation yes 1 2 R topics documented: R topics documented: marelac-package . .3 air_density . .5 air_spechum . .6 atmComp . .7 AtomicWeight . .8 Bathymetry . .9 Constants . 10 convert_p . 11 convert_RtoS . 11 convert_salinity . 13 convert_StoCl . 15 convert_StoR . 16 convert_T . 17 coriolis . 18 diffcoeff . 19 earth_surf . 21 gas_O2sat . 23 gas_satconc . 25 gas_schmidt . 27 gas_solubility . 28 gas_transfer . 31 gravity . 33 molvol . 34 molweight . 36 Oceans . 37 redfield . 38 ssd2rad . 39 sw_adtgrad . 40 sw_alpha . 41 sw_beta . 42 sw_comp . 43 sw_conserv . 44 sw_cp . 45 sw_dens . 47 sw_depth . 49 sw_enthalpy . 50 sw_entropy . 51 sw_gibbs . 52 sw_kappa .
    [Show full text]
  • Calculation Exercises with Answers and Solutions
    Atmospheric Chemistry and Physics Calculation Exercises Contents Exercise A, chapter 1 - 3 in Jacob …………………………………………………… 2 Exercise B, chapter 4, 6 in Jacob …………………………………………………… 6 Exercise C, chapter 7, 8 in Jacob, OH on aerosols and booklet by Heintzenberg … 11 Exercise D, chapter 9 in Jacob………………………………………………………. 16 Exercise E, chapter 10 in Jacob……………………………………………………… 20 Exercise F, chapter 11 - 13 in Jacob………………………………………………… 24 Answers and solutions …………………………………………………………………. 29 Note that approximately 40% of the written exam deals with calculations. The remainder is about understanding of the theory. Exercises marked with an asterisk (*) are for the most interested students. These exercises are more comprehensive and/or difficult than questions appearing in the written exam. 1 Atmospheric Chemistry and Physics – Exercise A, chap. 1 – 3 Recommended activity before exercise: Try to solve 1:1 – 1:5, 2:1 – 2:2 and 3:1 – 3:2. Summary: Concentration Example Advantage Number density No. molecules/m3, Useful for calculations of reaction kmol/m3 rates in the gas phase Partial pressure Useful measure on the amount of a substance that easily can be converted to mixing ratio Mixing ratio ppmv can mean e.g. Concentration relative to the mole/mole or partial concentration of air molecules. Very pressure/total pressure useful because air is compressible. Ideal gas law: PV = nRT Molar mass: M = m/n Density: ρ = m/V = PM/RT; (from the two equations above) Mixing ratio (vol): Cx = nx/na = Px/Pa ≠ mx/ma Number density: Cvol = nNav/V 26 -1 Avogadro’s
    [Show full text]
  • Lecture 3. the Basic Properties of the Natural Atmosphere 1. Composition
    Lecture 3. The basic properties of the natural atmosphere Objectives: 1. Composition of air. 2. Pressure. 3. Temperature. 4. Density. 5. Concentration. Mole. Mixing ratio. 6. Gas laws. 7. Dry air and moist air. Readings: Turco: p.11-27, 38-43, 366-367, 490-492; Brimblecombe: p. 1-5 1. Composition of air. The word atmosphere derives from the Greek atmo (vapor) and spherios (sphere). The Earth’s atmosphere is a mixture of gases that we call air. Air usually contains a number of small particles (atmospheric aerosols), clouds of condensed water, and ice cloud. NOTE : The atmosphere is a thin veil of gases; if our planet were the size of an apple, its atmosphere would be thick as the apple peel. Some 80% of the mass of the atmosphere is within 10 km of the surface of the Earth, which has a diameter of about 12,742 km. The Earth’s atmosphere as a mixture of gases is characterized by pressure, temperature, and density which vary with altitude (will be discussed in Lecture 4). The atmosphere below about 100 km is called Homosphere. This part of the atmosphere consists of uniform mixtures of gases as illustrated in Table 3.1. 1 Table 3.1. The composition of air. Gases Fraction of air Constant gases Nitrogen, N2 78.08% Oxygen, O2 20.95% Argon, Ar 0.93% Neon, Ne 0.0018% Helium, He 0.0005% Krypton, Kr 0.00011% Xenon, Xe 0.000009% Variable gases Water vapor, H2O 4.0% (maximum, in the tropics) 0.00001% (minimum, at the South Pole) Carbon dioxide, CO2 0.0365% (increasing ~0.4% per year) Methane, CH4 ~0.00018% (increases due to agriculture) Hydrogen, H2 ~0.00006% Nitrous oxide, N2O ~0.00003% Carbon monoxide, CO ~0.000009% Ozone, O3 ~0.000001% - 0.0004% Fluorocarbon 12, CF2Cl2 ~0.00000005% Other gases 1% Oxygen 21% Nitrogen 78% 2 • Some gases in Table 3.1 are called constant gases because the ratio of the number of molecules for each gas and the total number of molecules of air do not change substantially from time to time or place to place.
    [Show full text]
  • Interactions Between Polymers and Nanoparticles : Formation of « Supermicellar » Hybrid Aggregates
    1 Interactions between Polymers and Nanoparticles : Formation of « Supermicellar » Hybrid Aggregates J.-F. Berret@, K. Yokota* and M. Morvan, Complex Fluids Laboratory, UMR CNRS - Rhodia n°166, Cranbury Research Center Rhodia 259 Prospect Plains Road Cranbury NJ 08512 USA Abstract : When polyelectrolyte-neutral block copolymers are mixed in solutions to oppositely charged species (e.g. surfactant micelles, macromolecules, proteins etc…), there is the formation of stable “supermicellar” aggregates combining both components. The resulting colloidal complexes exhibit a core-shell structure and the mechanism yielding to their formation is electrostatic self-assembly. In this contribution, we report on the structural properties of “supermicellar” aggregates made from yttrium-based inorganic nanoparticles (radius 2 nm) and polyelectrolyte-neutral block copolymers in aqueous solutions. The yttrium hydroxyacetate particles were chosen as a model system for inorganic colloids, and also for their use in industrial applications as precursors for ceramic and opto-electronic materials. The copolymers placed under scrutiny are the water soluble and asymmetric poly(sodium acrylate)-b-poly(acrylamide) diblocks. Using static and dynamical light scattering experiments, we demonstrate the analogy between surfactant micelles and nanoparticles in the complexation phenomenon with oppositely charged polymers. We also determine the sizes and the aggregation numbers of the hybrid organic-inorganic 1 2 complexes. Several additional properties are discussed, such
    [Show full text]
  • Alkali Metal Vapor Pressures & Number Densities for Hybrid Spin Exchange Optical Pumping
    Alkali Metal Vapor Pressures & Number Densities for Hybrid Spin Exchange Optical Pumping Jaideep Singh, Peter A. M. Dolph, & William A. Tobias University of Virginia Version 1.95 April 23, 2008 Abstract Vapor pressure curves and number density formulas for the alkali metals are listed and compared from the 1995 CRC, Nesmeyanov, and Killian. Formulas to obtain the temperature, the dimer to monomer density ratio, and the pure vapor ratio given an alkali density are derived. Considerations and formulas for making a prescribed hybrid vapor ratio of alkali to Rb at a prescribed alkali density are presented. Contents 1 Vapor Pressure Curves 2 1.1TheClausius-ClapeyronEquation................................. 2 1.2NumberDensityFormulas...................................... 2 1.3Comparisonwithotherstandardformulas............................. 3 1.4AlkaliDimers............................................. 3 2 Creating Hybrid Mixes 11 2.1Predictingthehybridvaporratio.................................. 11 2.2Findingthedesiredmolefraction.................................. 11 2.3GloveboxMethod........................................... 12 2.4ReactionMethod........................................... 14 1 1 Vapor Pressure Curves 1.1 The Clausius-Clapeyron Equation The saturated vapor pressure above a liquid (solid) is described by the Clausius-Clapeyron equation. It is a consequence of the equality between the chemical potentials of the vapor and liquid (solid). The derivation can be found in any undergraduate text on thermodynamics (e.g. Kittel & Kroemer [1]): Δv · ∂P = L · ∂T/T (1) where P is the pressure, T is the temperature, L is the latent heat of vaporization (sublimation) per particle, and Δv is given by: Vv Vl(s) Δv = vv − vl(s) = − (2) Nv Nl(s) where V is the volume occupied by the particles, N is the number of particles, and the subscripts v & l(s) refer to the vapor & liquid (solid) respectively.
    [Show full text]
  • Receive! Osti
    DOE/MC/30175-5033 (DE96000569) RECEIVE! NOV 2 11995 OSTI Portable Sensor for Hazardous Waste Topical Report October 1993 - September 1994 Dr. Lawrence G. Piper October 1994 Work Performed Under Contract No.: DE-AC21-93MC30175 For U.S. Department of Energy U.S. Department of Energy Office of Environmental Management Office of Fossil Energy Office of Technology Development Morgantown Energy Technology Center Washington, DC Morgantown, West Virginia By Physical Sciences Inc. Andover, Massachusetts IAS DISTRIBUTION DP TMi.Q nnpiiycwr » I !MI IS UTT-n, S\c^ DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manu• facturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. This report has been reproduced directly from the best available copy. Available to DOE and DOE contractors from the Office of Scientific and Technical Information, 175 Oak Ridge Turnpike, Oak Ridge, TN 37831; prices available at (615) 576-8401. Available to the public from the National Technical Information Service, U.S.
    [Show full text]
  • Enter Or Copy the Title of the Article Here
    This is the author’s final, peer-reviewed manuscript as accepted for publication. The publisher-formatted version may be available through the publisher’s web site or your institution’s library. Kirkwood–Buff integrals for ideal solutions Elizabeth A. Ploetz, Nikolaos Bentenitis, Paul E. Smith. How to cite this manuscript If you make reference to this version of the manuscript, use the following information: Ploetz, E.A., Bentenitis, N., & Smith, P.E. (2010). Kirkwood–Buff integrals for ideal solutions. Retrieved from http://krex.ksu.edu Published Version Information Citation: Ploetz, E.A., Bentenitis, N., & Smith, P.E. (2010). Kirkwood–Buff integrals for ideal solutions. The journal of chemical physics, 132(16), 9. Copyright: © 2010 American Institute of Physics. Digital Object Identifier (DOI): doi:10.1063/1.3398466 Publisher’s Link: http://jcp.aip.org/resource/1/jcpsa6/v132/i16/p164501_s1 This item was retrieved from the K-State Research Exchange (K-REx), the institutional repository of Kansas State University. K-REx is available at http://krex.ksu.edu THE JOURNAL OF CHEMICAL PHYSICS 132, 164501 ͑2010͒ Kirkwood–Buff integrals for ideal solutions ͒ Elizabeth A. Ploetz,1 Nikolaos Bentenitis,2 and Paul E. Smith1,a 1Department of Chemistry, Kansas State University, Manhattan, Kansas 66506, USA 2Department of Chemistry and Biochemistry, Southwestern University, Georgetown, Texas 78626, USA ͑Received 20 May 2009; accepted 29 March 2010; published online 22 April 2010͒ The Kirkwood–Buff ͑KB͒ theory of solutions is a rigorous theory of solution mixtures which relates the molecular distributions between the solution components to the thermodynamic properties of the mixture. Ideal solutions represent a useful reference for understanding the properties of real solutions.
    [Show full text]
  • Density Lab B Test
    Northern Regional: January 19th, 2019 Density Lab B Test Name(s): _______________________________________________________________________ Team Name: ________________________________________ School Name: ________________________________________ Rank: ___________ Team Number: ___________ Score: ___________ Written Test 1) All of the below are types of densities except (5 points) a) Mass Density b) Number Density c) Area Density d) Volume Density 2) Which of the following exhibits Boyle’s Law? (5 points) a) P1V1= P2V2 b) P1/T1=P2/T2 c) PV= nRT d) V1/T1=V2/T2 3) How many atoms are in 3 moles of a substance? (5 points) 23 a) 24.023*10 atoms​ ​ 24 b) 1.81*10 ​ atoms ​ c) 23 atoms 23 d) 6.02310 atoms​ ​ 4) If the temperature of a container doubled, what would have happened to the pressure of the gas inside the container? (5 points) a) Halved b) Doubled c) Quadrupled d) Nothing 5) What factors affect density? (5 points) a) Pressure b) Temperature c) Both A and B d) None of the above 6) Water is more dense as a solid. (5 points) a) True b) False 7) Pascal is the SI Unit for pressure. (5 points) a) True b) False 8) The acceleration due to gravity on Earth is 9.8 m/s. (5 points) a) True b) False 9) Salt water is more dense than deionized water. (5 points) a) True b) False 10) By Archimedes' principle, the buoyant force is equal to the weight of fluid displaced. (5 points) a) True b) False 11) What is the Archimedes Principle? (5 points) 12) What is the molarity of a solution containing 18.9 grams of RuCl3 in enough water to ​ ​ make 1.00 L of solution?
    [Show full text]
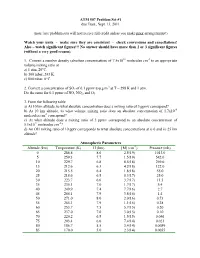
  • Problem Set #1 Due Tues., Sept
    ATM 507 Problem Set #1 due Tues., Sept. 13, 2011 (note: late problem sets will not receive full credit unless you make prior arrangements!) Watch your units - make sure they are consistent - check conversions and cancellations! Also – watch significant figures!!! No answer should have more than 2 or 3 significant figures (without a very good reason). 1. Convert a number density (absolute concentration) of 7.5x1012 molecules cm-3 to an appropriate volume mixing ratio at a) 1 atm, 20°C. b) 100 mbar, 243 K. c) 800 mbar, 0°C. -3 2. Convert a concentration of SO2 of 0.1 ppmv to μg m at T = 298 K and 1 atm. Do the same for 0.1 ppmv of NO, NO2, and O3. 3. From the following table a) At 10 km altitude, to what absolute concentration does a mixing ratio of 3 ppmv correspond? b) At 10 km altitude, to what volume mixing ratio does an absolute concentration of 1.7x1010 molecules cm-3 correspond? c) At what altitude does a mixing ratio of 3 ppmv correspond to an absolute concentration of 5.1x1011 molecules cm-3? d) An OH mixing ratio of 10 pptv corresponds to what absolute concentrations at i) 0 and ii) 25 km altitude? Atmospheric Parameters Altitude (km) Temperature (K) H (km) [M] (cm-3) Pressure (mb) 0 288.8 8.6 2.5(19) 1013.0 5 259.3 7.7 1.5(19) 542.0 10 229.7 6.8 8.5(18) 269.0 15 212.6 6.3 4.2(18) 122.0 20 215.5 6.4 1.8(18) 55.0 25 218.6 6.5 8.3(17) 25.0 30 223.7 6.6 3.7(17) 11.5 35 235.1 7.0 1.7(17) 5.4 40 249.9 7.4 7.7(16) 2.7 45 266.1 7.9 3.8(16) 1.4 50 271.0 8.0 2.0(16) 0.73 55 265.3 7.9 1.1(16) 0.38 60 253.7 7.5 5.7(15) 0.20 65 237.0 7.0 3.0(15) 0.10 70 220.2 6.5 1.5(15) 0.046 75 203.4 6.0 7.4(14) 0.021 80 186.7 5.5 3.4(14) 0.0089 85 170.0 5.0 2.3(14) 0.0055 4.
    [Show full text]