DOCSLIB.ORG

Learning Better Lossless Compression Using Lossy Compression

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Learning Better Lossless Compression Using Lossy Compression Learning Better Lossless Compression Using Lossy Compression Fabian Mentzer Luc Van Gool Michael Tschannen ETH Zurich ETH Zurich Google Research, Brain Team [email protected] [email protected] [email protected] Abstract xl x <latexit sha1_base64="FCgE+SeO51rbUyQCgOO9cG+tGjw=">AAAB6nicbVDJSgNBEK2JW4xbXG5eGoPgKcxEQU8S8OIxolkgGUJPpyZp0tMzdPeIYcgnePGgiFe/yJt/Y2c5aOKDgsd7VVTVCxLBtXHdbye3srq2vpHfLGxt7+zuFfcPGjpOFcM6i0WsWgHVKLjEuuFGYCtRSKNAYDMY3kz85iMqzWP5YEYJ+hHtSx5yRo2V7p+6olssuWV3CrJMvDkpVY9gilq3+NXpxSyNUBomqNZtz02Mn1FlOBM4LnRSjQllQ9rHtqWSRqj9bHrqmJxapUfCWNmShkzV3xMZjbQeRYHtjKgZ6EVvIv7ntVMTXvkZl0lqULLZojAVxMRk8jfpcYXMiJEllClubyVsQBVlxqZTsCF4iy8vk0al7J2XK3cXper1LA3IwzGcwBl4cAlVuIUa1IFBH57hFd4c4bw4787HrDXnzGcO4Q+czx/XUo4v</latexit> l BPG <latexit sha1_base64="SY0uayGBkROUrzaICLpYrvJshQs=">AAACv3icbVFda9swFFW8ry77Sre97UUsDNoRgp0NNhgZGXvZYwdLW7BNuJavExFJNpLc1DP+HXvZ6/af9m8mOy20TS8Ijs7RvUf33qQQ3Fjf/9fz7ty9d//B3sP+o8dPnj4b7D8/NnmpGc5ZLnJ9moBBwRXOLbcCTwuNIBOBJ8n6a6ufnKE2PFc/bFVgLGGpeMYZWEctBoOoq1EvNVQNPV+IxWDoj/0u6C4ILsBw9pJ0cbTY7/2K0pyVEpVlAowJA7+wcQ3aciaw6UelwQLYGpYYOqhAoonrzrahbxyT0izX7ihLO/ZqRg3SmEom7qUEuzI3tZa8VTu/NNiVEnkbHZY2+xjXXBWlRcW2X8tKQW1O28nRlGtkVlQOANPcdUfZCjQw6+Z7zcDy9U/Xt8INy6UElb6NGNduGGkYxHXUyuHl0qYHbZFxez2M6z69EpHKUwzNCgqcbvNHGRdiullxi6NUw2bElUJNnfN04mZOu1qHtB4GzaemcasMbi5uFxxPxsG78eT7++Hs83anZI+8Iq/JAQnIBzIj38gRmRNGzshv8of89b54S095xfap17vIeUGuhVf9B7+92bM=</latexit> We leverage the powerful lossy image compression al- gorithm BPG to build a lossless image compression sys- QC RC RC tem. Specifically, the original image is first decomposed + <latexit sha1_base64="VYjfhLw3lH1NsTscrWXm90QWm30=">AAACu3icbVFda9swFFW8ry776sfe9iIWBu0Iwc4GGxSXwF722MHSFmyvXMvXiRZJNpK8NDP+Hdvr9q/2byY7LbRNLwiOztG9R/fetBTcWN//1/Pu3X/w8NHW4/6Tp8+ev9je2T0xRaUZTlkhCn2WgkHBFU4ttwLPSo0gU4Gn6eJTq5/+QG14ob7aVYmJhJniOWdgHfUt7irUMw2rhl6cbw/8kd8F3QTBJRhMXpIujs93er/irGCVRGWZAGOiwC9tUoO2nAls+nFlsAS2gBlGDiqQaJK6M23oG8dkNC+0O8rSjr2eUYM0ZiVT91KCnZvbWkveqV1cGWxKqbyLjiqbf0xqrsrKomLrr+WVoLag7dRoxjUyK1YOANPcdUfZHDQw62Z7w8DyxU/Xt8IlK6QElb2NGdduGFkUJHXcytHVwsL9tsiovR4kdZ9ei1gVGUZmDiWG6/xhzoUIl3NucZhpWA65Uqipcw7Hbua0q3VA60HQHDaNW2Vwe3Gb4GQ8Ct6Nxl/eDyZH652SLfKKvCb7JCAfyIR8JsdkShjR5Df5Q/56oce8755YP/V6lzl75EZ41X8Hvtij</latexit> x into the lossy reconstruction obtained after compressing it <latexit sha1_base64="1kNcN2IiPamqSzlJt9OuLPtgnQo=">AAAB6HicbVDLTgJBEOzFF+ILHzcvE4mJJ7KLJnoyJF48QiJIAhsyO/TCyOzsZmbWSAhf4MWDxnj1k7z5Nw4LBwUr6aRS1Z3uriARXBvX/XZyK6tr6xv5zcLW9s7uXnH/oKnjVDFssFjEqhVQjYJLbBhuBLYShTQKBN4Hw5upf/+ISvNY3plRgn5E+5KHnFFjpfpTt1hyy24Gsky8OSlVjyBDrVv86vRilkYoDRNU67bnJsYfU2U4EzgpdFKNCWVD2se2pZJGqP1xduiEnFqlR8JY2ZKGZOrviTGNtB5Fge2MqBnoRW8q/ue1UxNe+WMuk9SgZLNFYSqIicn0a9LjCpkRI0soU9zeStiAKsqMzaZgQ/AWX14mzUrZOy9X6hel6vUsDcjDMZzAGXhwCVW4hRo0gAHCM7zCm/PgvDjvzsesNefMZw7hD5zPH1h+jVA=</latexit> x <latexit sha1_base64="T2anKYaMGRZ5lXVzxQUOz1CFtFo=">AAAC03icbVFNb9MwGHbD1yhfHRy5WLRDG1RVUg6bQEWVuHAcEt0mJVHlOG9bq7YT2Q5dsXJBnJB25j/sxBX+BUf+DU66Stu6V7L0+Hne7zfJOdPG9/81vFu379y9t3W/+eDho8dPWttPj3RWKAojmvFMnSREA2cSRoYZDie5AiISDsfJ/EOlH38BpVkmP5tlDrEgU8kmjBLjqHGrExk4NXUeO1VkWdqIMkU5pLYTJcK+LjtlOW61/Z5fG94EwQVoD3fOz9/+PXt5ON5u/IzSjBYCpKGcaB0Gfm5iS5RhLnfZjAoNOaFzMoXQQUkE6NjWbZR4xzEpnmTKPWlwzV6OsERovRSJ8xTEzPR1rSJv1E7XBTalRNxEh4WZHMSWybwwIOmqtUnBsclwtU2cMgXU8KUDhCrmpsN0RhShxu38SgHD5l/d3BIWNBOCyPTVetFhENuoksP1IQe7VZJe9d2LbRNfskhmKYR6RnIYrOK7E8b5YDFjBrqpIosukxIUdpUHfbdzXOfaw7YdlO/qUwbXD7cJjvq94E2v/yloD9+jlW2h5+gF2kUB2kdD9BEdohGi6Af6hX6jP97Is9437/vK1WtcxDxDV8w7+w+96eW1</latexit> <latexit sha1_base64="Z96E99LFNgyTtBLMezyLVQfMhCE=">AAAC1HicbVFdb9MwFHXDx0b56gZvvFh0kzZUqqR7YBIqqsQLj0Oi3aQkqhznZrVqO5Ht0BWTJ8QTEq/8Dl7hl/BvcNJV2tZdKdLxOb73xOcmBWfa+P6/lnfn7r37W9sP2g8fPX7ytLOzO9F5qSiMac5zdZYQDZxJGBtmOJwVCohIOJwm8/e1fvoZlGa5/GSWBcSCnEuWMUqMo6ad/YgyRTmkNjJwYZqBNuGEziu7FyXCvq72qmra6fp9vym8CYJL0B09R02dTHdav6I0p6UAaSgnWoeBX5jYEmWYc6vaUamhcC7kHEIHJRGgY9vYV3jfMSnOcuU+aXDDXu2wRGi9FIm7KYiZ6ZtaTd6qXawNNqVE3EaHpcmOY8tkURqQdPVrWcmxyXEdJ06ZAmr40gFCFXOvw3RGFKHGhX7NwLD5F/duCQuaC0Fk+modfRjELn0nh+tNDg/qIf36eBjbNr5SkcxTCPWMFDBc9fcyxvlwMWMGeqkiix6TEhR2zsOByxw3sw6x7QbV22aVwc3FbYLJoB8c9Qcfg+7o3WqnaBu9QC/RAQrQGzRCH9AJGiOKfqDf6A/66028r9437/vqqte67HmGrpX38z/27uLo</latexit> − with BPG and the corresponding residual. We then model p(r xl) p(r xl) the distribution of the residual with a convolutional neu- <latexit sha1_base64="9q+K4qK6hF6bq4VkdAfWgFffsfE=">AAAB73icbVDLSgNBEOz1GeMrPm5eBoMQL2E3CnqSgBePEcwDkiXMTmaTIbOz48ysGNb8hBcPinj1d7z5N042OWhiQUNR1U13VyA508Z1v52l5ZXVtfXcRn5za3tnt7C339Bxogitk5jHqhVgTTkTtG6Y4bQlFcVRwGkzGF5P/OYDVZrF4s6MJPUj3BcsZAQbK7VkST09dvlpt1B0y24GtEi8GSlWDyFDrVv46vRikkRUGMKx1m3PlcZPsTKMcDrOdxJNJSZD3KdtSwWOqPbT7N4xOrFKD4WxsiUMytTfEymOtB5Fge2MsBnoeW8i/ue1ExNe+ikTMjFUkOmiMOHIxGjyPOoxRYnhI0swUczeisgAK0yMjShvQ/DmX14kjUrZOytXbs+L1atpGpCDIziGEnhwAVW4gRrUgQCHZ3iFN+feeXHenY9p65IzmzmAP3A+fwAm05AQ</latexit> | <latexit sha1_base64="kdKRmLR3/WeLs/x2QLngL0+K1sw=">AAACxHicbVFda9swFFXcfXTZV7qPp72IhUEyQrDTQgcjIzAYe+xgaQu2CbJ8nYhIspHkpqnm/Y0973X7Rfs3k50W2qYXBEfn6N6je29ScKaN7/9reTv37j94uPuo/fjJ02fPO3svjnVeKgpTmvNcnSZEA2cSpoYZDqeFAiISDifJ8nOtn5yB0iyX3826gFiQuWQZo8Q4atZ5HTU17FyRdYWLnvpxPuP9WafrD/0m8DYILkF38go1cTTba/2K0pyWAqShnGgdBn5hYkuUYZRD1Y5KDQWhSzKH0EFJBOjYNt4VfueYFGe5ckca3LDXMywRWq9F4l4KYhb6tlaTd2rnVwbbUiLuosPSZB9iy2RRGpB087Ws5NjkuB4fTpkCavjaAUIVc91huiCKUOOGfMPAsOWF61vCiuZCEJm+jyhTbhhpGMQ2quXwanPjXl1kWF/7sW3jaxHJPIVQL0gB403+IGOcj1cLZmCQKrIaMClBYec8HrmZ46ZWH9tuUH2sKrfK4PbitsHxaBjsD0ffDrqTT5udol30Br1FPRSgQzRBX9ERmiKKLPqN/qC/3hePe9orN0+91mXOS3QjvJ//AXwA25Q=</latexit> | ral network-based probabilistic model that is conditioned AC ACAC on the BPG reconstruction, and combine it with entropy r r coding to losslessly encode the residual. Finally, the im- Figure 1. Overview of the proposed learned lossless compression age is stored using the concatenation of the bitstreams pro- approach. To encode an input image x, we feed it into the Q- duced by BPG and the learned residual coder. The resulting Classifier (QC) CNN to obtain an appropriate quantization param- compression system achieves state-of-the-art performance eter Q, which is used to compress x with BPG. The resulting lossy in learned lossless full-resolution image compression, out- reconstruction xl is fed into the Residual Compressor (RC) CNN, performing previous learned approaches as well as PNG, which predicts the probability distribution of the residual, p(rjxl), WebP, and JPEG2000. conditionally on xl. An arithmetic coder (AC) encodes the resid- ual r to a bitstream, given p(rjxl). In gray we visualize how to reconstruct x from the bistream. Learned components are shown in violet. 1. Introduction The need to efficiently store the ever growing amounts of overhead incurred by using an imprecise model of the data data generated continuously on mobile devices has spurred distribution. One beautiful result is that maximizing the a lot of research on compression algorithms. Algorithms likelihood of a parametric probabilistic model is equivalent like JPEG [51] for images and H.264 [53] for videos are to minimizing the bitrate obtained when using that model used by billions of people daily. for lossless compression with an entropy coder (see, e.g., After the breakthrough results achieved with deep neu- [29]). Learning parametric probabilistic models by likeli- ral networks in image classification [27], and the subse- hood maximization has been studied to a great extent in the quent rise of deep-learning based methods, learned lossy generative modeling literature (e.g. [50, 49, 39, 34, 25]). arXiv:2003.10184v1 [cs.CV] 23 Mar 2020 image compression has emerged as an active area of re- Recent works have linked these results to learned lossless search (e.g. [6, 45, 46, 37,2,4, 30, 28, 48]). In lossy compression [29, 18, 47, 24]. compression, the goal is to achieve small bitrates R given Even though recent learned lossy image compression a certain allowed distortion D in the reconstruction, i.e., methods achieve state-of-the-art results on various data the rate-distortion trade-off R + λD is optimized. In con- sets, the results obtained by the non-learned H.265-based trast, in lossless compression, no distortion is allowed, and BPG [43,7] are still highly competitive, without requir- we aim to reconstruct the input perfectly by transmitting ing sophisticated hardware accelerators such as GPUs to as few bits as possible. To this end, a probabilistic model run. While BPG was outperformed by learning-based ap- of the data can be used together with entropy coding tech- proaches across the bitrate spectrum in terms of PSNR [30] niques to encode and transmit data via a bitstream. The and visual quality [4], it still excels particularly at high- theoretical foundation for this idea is given in Shannon’s PSNR lossy reconstructions. landmark paper [40], which proves a lower bound for the In this paper, we propose a learned lossless compres- bitrate achievable by such a probabilistic model, and the sion system by leveraging the power of the lossy BPG, as 1 illustrated in Fig.1. Specifically, we decompose the in- boom et al.[18] propose Integer Discrete Flows (IDFs), put image x into the lossy reconstruction xl produced by defining an invertible transformation for discrete data. In BPG and the corresponding residual r. We then learn a contrast to L3C, the latter works focus on smaller data sets probabilistic model p(r x ) of the residual, conditionally such as MNIST, CIFAR-10, ImageNet32, and ImageNet64, j l on the lossy reconstruction xl. This probabilistic model is where they achieve state-of-the-art results. fully convolutional and can be evaluated using a single for- ward
Load more

Recommended publications
  • Free Lossless Image Format
    FREE LOSSLESS IMAGE FORMAT Jon Sneyers and Pieter Wuille [email protected] [email protected] Cloudinary Blockstream ICIP 2016, September 26th DON’T WE HAVE ENOUGH IMAGE FORMATS ALREADY? • JPEG, PNG, GIF, WebP, JPEG 2000, JPEG XR, JPEG-LS, JBIG(2), APNG, MNG, BPG, TIFF, BMP, TGA, PCX, PBM/PGM/PPM, PAM, … • Obligatory XKCD comic: YES, BUT… • There are many kinds of images: photographs, medical images, diagrams, plots, maps, line art, paintings, comics, logos, game graphics, textures, rendered scenes, scanned documents, screenshots, … EVERYTHING SUCKS AT SOMETHING • None of the existing formats works well on all kinds of images. • JPEG / JP2 / JXR is great for photographs, but… • PNG / GIF is great for line art, but… • WebP: basically two totally different formats • Lossy WebP: somewhat better than (moz)JPEG • Lossless WebP: somewhat better than PNG • They are both .webp, but you still have to pick the format GOAL: ONE FORMAT THAT COMPRESSES ALL IMAGES WELL EXPERIMENTAL RESULTS Corpus Lossless formats JPEG* (bit depth) FLIF FLIF* WebP BPG PNG PNG* JP2* JXR JLS 100% 90% interlaced PNGs, we used OptiPNG [21]. For BPG we used [4] 8 1.002 1.000 1.234 1.318 1.480 2.108 1.253 1.676 1.242 1.054 0.302 the options -m 9 -e jctvc; for WebP we used -m 6 -q [4] 16 1.017 1.000 / / 1.414 1.502 1.012 2.011 1.111 / / 100. For the other formats we used default lossless options. [5] 8 1.032 1.000 1.099 1.163 1.429 1.664 1.097 1.248 1.500 1.017 0.302� [6] 8 1.003 1.000 1.040 1.081 1.282 1.441 1.074 1.168 1.225 0.980 0.263 Figure 4 shows the results; see [22] for more details.
    [Show full text]
  • How to Exploit the Transferability of Learned Image Compression to Conventional Codecs
    How to Exploit the Transferability of Learned Image Compression to Conventional Codecs Jan P. Klopp Keng-Chi Liu National Taiwan University Taiwan AI Labs [email protected] [email protected] Liang-Gee Chen Shao-Yi Chien National Taiwan University [email protected] [email protected] Abstract Lossy compression optimises the objective Lossy image compression is often limited by the sim- L = R + λD (1) plicity of the chosen loss measure. Recent research sug- gests that generative adversarial networks have the ability where R and D stand for rate and distortion, respectively, to overcome this limitation and serve as a multi-modal loss, and λ controls their weight relative to each other. In prac- especially for textures. Together with learned image com- tice, computational efficiency is another constraint as at pression, these two techniques can be used to great effect least the decoder needs to process high resolutions in real- when relaxing the commonly employed tight measures of time under a limited power envelope, typically necessitating distortion. However, convolutional neural network-based dedicated hardware implementations. Requirements for the algorithms have a large computational footprint. Ideally, encoder are more relaxed, often allowing even offline en- an existing conventional codec should stay in place, ensur- coding without demanding real-time capability. ing faster adoption and adherence to a balanced computa- Recent research has developed along two lines: evolu- tional envelope. tion of exiting coding technologies, such as H264 [41] or As a possible avenue to this goal, we propose and investi- H265 [35], culminating in the most recent AV1 codec, on gate how learned image coding can be used as a surrogate the one hand.
    [Show full text]
  • Download This PDF File
    Sindh Univ. Res. Jour. (Sci. Ser.) Vol.47 (3) 531-534 (2015) I NDH NIVERSITY ESEARCH OURNAL ( CIENCE ERIES) S U R J S S Performance Analysis of Image Compression Standards with Reference to JPEG 2000 N. MINALLAH++, A. KHALIL, M. YOUNAS, M. FURQAN, M. M. BOKHARI Department of Computer Systems Engineering, University of Engineering and Technology, Peshawar Received 12thJune 2014 and Revised 8th September 2015 Abstract: JPEG 2000 is the most widely used standard for still image coding. Some other well-known image coding techniques include JPEG, JPEG XR and WEBP. This paper provides performance evaluation of JPEG 2000 with reference to other image coding standards, such as JPEG, JPEG XR and WEBP. For the performance evaluation of JPEG 2000 with reference to JPEG, JPEG XR and WebP, we considered divers image coding scenarios such as continuous tome images, grey scale images, High Definition (HD) images, true color images and web images. Each of the considered algorithms are briefly explained followed by their performance evaluation using different quality metrics, such as Peak Signal to Noise Ratio (PSNR), Mean Square Error (MSE), Structure Similarity Index (SSIM), Bits Per Pixel (BPP), Compression Ratio (CR) and Encoding/ Decoding Complexity. The results obtained showed that choice of the each algorithm depends upon the imaging scenario and it was found that JPEG 2000 supports the widest set of features among the evaluated standards and better performance. Keywords: Analysis, Standards JPEG 2000. performance analysis, followed by Section 6 with 1. INTRODUCTION There are different standards of image compression explanation of the considered performance analysis and decompression.
    [Show full text]
  • Neural Multi-Scale Image Compression
    Neural Multi-scale Image Compression Ken Nakanishi 1 Shin-ichi Maeda 2 Takeru Miyato 2 Daisuke Okanohara 2 Abstract 1.00 This study presents a new lossy image compres- sion method that utilizes the multi-scale features 0.98 of natural images. Our model consists of two networks: multi-scale lossy autoencoder and par- 0.96 allel multi-scale lossless coder. The multi-scale Proposed 0.94 JPEG lossy autoencoder extracts the multi-scale image MS-SSIM WebP features to quantized variables and the parallel BPG 0.92 multi-scale lossless coder enables rapid and ac- Johnston et al. Rippel & Bourdev curate lossless coding of the quantized variables 0.90 via encoding/decoding the variables in parallel. 0.0 0.2 0.4 0.6 0.8 1.0 Our proposed model achieves comparable perfor- Bits per pixel mance to the state-of-the-art model on Kodak and RAISE-1k dataset images, and it encodes a PNG image of size 768 × 512 in 70 ms with a single Figure 1. Rate-distortion trade off curves with different methods GPU and a single CPU process and decodes it on Kodak dataset. The horizontal axis represents bits-per-pixel into a high-fidelity image in approximately 200 (bpp) and the vertical axis represents multi-scale structural similar- ms. ity (MS-SSIM). Our model achieves better or comparable bpp with respect to the state-of-the-art results (Rippel & Bourdev, 2017). 1. Introduction K Data compression for video and image data is a crucial tech- via ML algorithm is not new. The -means algorithm was nique for reducing communication traffic and saving data used for vector quantization (Gersho & Gray, 2012), and storage.
    [Show full text]
  • Arxiv:2002.01657V1 [Eess.IV] 5 Feb 2020 Port Lossless Model to Compress Images Lossless
    LEARNED LOSSLESS IMAGE COMPRESSION WITH A HYPERPRIOR AND DISCRETIZED GAUSSIAN MIXTURE LIKELIHOODS Zhengxue Cheng, Heming Sun, Masaru Takeuchi, Jiro Katto Department of Computer Science and Communications Engineering, Waseda University, Tokyo, Japan. ABSTRACT effectively in [12, 13, 14]. Some methods decorrelate each Lossless image compression is an important task in the field channel of latent codes and apply deep residual learning to of multimedia communication. Traditional image codecs improve the performance as [15, 16, 17]. However, deep typically support lossless mode, such as WebP, JPEG2000, learning based lossless compression has rarely discussed. FLIF. Recently, deep learning based approaches have started One related work is L3C [18] to propose a hierarchical archi- to show the potential at this point. HyperPrior is an effective tecture with 3 scales to compress images lossless. technique proposed for lossy image compression. This paper In this paper, we propose a learned lossless image com- generalizes the hyperprior from lossy model to lossless com- pression using a hyperprior and discretized Gaussian mixture pression, and proposes a L2-norm term into the loss function likelihoods. Our contributions mainly consist of two aspects. to speed up training procedure. Besides, this paper also in- First, we generalize the hyperprior from lossy model to loss- vestigated different parameterized models for latent codes, less compression model, and propose a loss function with L2- and propose to use Gaussian mixture likelihoods to achieve norm for lossless compression to speed up training. Second, adaptive and flexible context models. Experimental results we investigate four parameterized distributions and propose validate our method can outperform existing deep learning to use Gaussian mixture likelihoods for the context model.
    [Show full text]
  • Image Formats
    Image Formats Ioannis Rekleitis Many different file formats • JPEG/JFIF • Exif • JPEG 2000 • BMP • GIF • WebP • PNG • HDR raster formats • TIFF • HEIF • PPM, PGM, PBM, • BAT and PNM • BPG CSCE 590: Introduction to Image Processing https://en.wikipedia.org/wiki/Image_file_formats 2 Many different file formats • JPEG/JFIF (Joint Photographic Experts Group) is a lossy compression method; JPEG- compressed images are usually stored in the JFIF (JPEG File Interchange Format) >ile format. The JPEG/JFIF >ilename extension is JPG or JPEG. Nearly every digital camera can save images in the JPEG/JFIF format, which supports eight-bit grayscale images and 24-bit color images (eight bits each for red, green, and blue). JPEG applies lossy compression to images, which can result in a signi>icant reduction of the >ile size. Applications can determine the degree of compression to apply, and the amount of compression affects the visual quality of the result. When not too great, the compression does not noticeably affect or detract from the image's quality, but JPEG iles suffer generational degradation when repeatedly edited and saved. (JPEG also provides lossless image storage, but the lossless version is not widely supported.) • JPEG 2000 is a compression standard enabling both lossless and lossy storage. The compression methods used are different from the ones in standard JFIF/JPEG; they improve quality and compression ratios, but also require more computational power to process. JPEG 2000 also adds features that are missing in JPEG. It is not nearly as common as JPEG, but it is used currently in professional movie editing and distribution (some digital cinemas, for example, use JPEG 2000 for individual movie frames).
    [Show full text]
  • Comparison of JPEG's Competitors for Document Images
    Comparison of JPEG’s competitors for document images Mostafa Darwiche1, The-Anh Pham1 and Mathieu Delalandre1 1 Laboratoire d’Informatique, 64 Avenue Jean Portalis, 37200 Tours, France e-mail: fi[email protected] Abstract— In this work, we carry out a study on the per- in [6] concerns assessing quality of common image formats formance of potential JPEG’s competitors when applied to (e.g., JPEG, TIFF, and PNG) that relies on optical charac- document images. Many novel codecs, such as BPG, Mozjpeg, ter recognition (OCR) errors and peak signal to noise ratio WebP and JPEG-XR, have been recently introduced in order to substitute the standard JPEG. Nonetheless, there is a lack of (PSNR) metric. The authors in [3] compare the performance performance evaluation of these codecs, especially for a particular of different coding methods (JPEG, JPEG 2000, MRC) using category of document images. Therefore, this work makes an traditional PSNR metric applied to several document samples. attempt to provide a detailed and thorough analysis of the Since our target is to provide a study on document images, aforementioned JPEG’s competitors. To this aim, we first provide we then use a large dataset with different image resolutions, a review of the most famous codecs that have been considered as being JPEG replacements. Next, some experiments are performed compress them at very low bit-rate and after that evaluate the to study the behavior of these coding schemes. Finally, we extract output images using OCR accuracy. We also take into account main remarks and conclusions characterizing the performance the PSNR measure to serve as an additional quality metric.
    [Show full text]
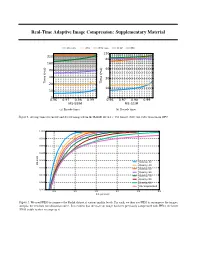
  • Real-Time Adaptive Image Compression: Supplementary Material
    Real-Time Adaptive Image Compression: Supplementary Material WaveOne JPEG JPEG 2000 WebP BPG 120 320 80 160 80 40 40 20 Time (ms) 20 Time (ms) 10 10 5 5 0.96 0.97 0.98 0.99 0.96 0.97 0.98 0.99 MS-SSIM MS-SSIM (a) Encode times. (b) Decode times. Figure 1. Average times to encode and decode images from the RAISE-1k 512 × 768 dataset. Note our codec was run on GPU. 1.000 0.995 0.990 0.985 0.980 Quality 30 MS-SSIM Quality 40 0.975 Quality 50 Quality 60 0.970 Quality 70 Quality 80 0.965 Quality 90 Uncompressed 0.960 0.5 1.0 1.5 2.0 2.5 3.0 Bits per pixel Figure 2. We used JPEG to compress the Kodak dataset at various quality levels. For each, we then use JPEG to recompress the images, and plot the resultant rate-distortion curve. It is evident that the more an image has been previously compressed with JPEG, the better JPEG is able to then recompress it. information across different scales. In SectionWe 4 average of these the to main attain textreconstruction. we the We discuss accumulate final the scalar value motivation outputs for along providedtargets these branches to and architectural constructed the choices along the the in reconstructions. objective processing more sigmoid pipeline, The detail. Figure function. branched goal 3. out of at This the different multiscale depths. discriminator architecture is allows to aggregating infer which of the two inputs is then the real target, and which is its Target The architecture of the discriminator used in our adversarial training procedure.
    [Show full text]
  • An Improved Objective Metric to Predict Image Quality Using Deep Neural Networks
    https://doi.org/10.2352/ISSN.2470-1173.2019.12.HVEI-214 © 2019, Society for Imaging Science and Technology An Improved Objective Metric to Predict Image Quality using Deep Neural Networks Pinar Akyazi and Touradj Ebrahimi; Multimedia Signal Processing Group (MMSPG); Ecole Polytechnique Fed´ erale´ de Lausanne; CH 1015, Lausanne, Switzerland Abstract ages in a full reference (FR) framework, i.e. when the reference Objective quality assessment of compressed images is very image is available, is a difference-based metric called the peak useful in many applications. In this paper we present an objec- signal to noise ratio (PSNR). PSNR and its derivatives do not tive quality metric that is better tuned to evaluate the quality of consider models based on the human visual system (HVS) and images distorted by compression artifacts. A deep convolutional therefore often result in low correlations with subjective quality neural networks is used to extract features from a reference im- ratings. [1]. Metrics such as structural similarity index (SSIM) age and its distorted version. Selected features have both spatial [2], multi-scale structural similarity index (MS-SSIM) [3], feature and spectral characteristics providing substantial information on similarity index (FSIM) [4] and visual information fidelity (VIF) perceived quality. These features are extracted from numerous [5] use models motivated by HVS and natural scenes statistics, randomly selected patches from images and overall image qual- resulting in better correlations with viewers’ opinion. ity is computed as a weighted sum of patch scores, where weights Numerous machine learning based objective quality metrics are learned during training. The model parameters are initialized have been reported in the literature.
    [Show full text]
  • JPEG 2000 and Google Books
    JPEG2000 and Google Books Jeff Breidenbach Google's mission is to organize the world's information and make it universally accessible and useful. Mass digitization • broad coverage • iteratively improve quality (reprocess, rescan) • more than XXM books out of XXXM since 2004 • XXX nominal pages per book • billions of images, petabytes of data JPEG2000 • pre-processed images • processed illustrations and color images • library return format • illustrations inside PDF files Jhove (Rel. 1.4, 2009-07-30) XTSize: 1165 Date: 2011-05-03 20:06:36 PDT YTSize: 2037 RepresentationInformation: 00000001.jp2 XTOSize: 0 ReportingModule: JPEG2000-hul, Rel. 1.3 (2007-01-08) YTOSize: 0 LastModified: 2006-09-22 11:01:00 PDT CSize: 3 Jhove Size: 231249 SSize: 7, 1, 1 Format: JPEG 2000 XRSize: 7, 1, 1 Status: Well-Formed and valid YRSize: 7, 1, 1 SignatureMatches: CodingStyleDefault: JPEG2000-hul CodingStyle: 0 MIMEtype: image/jp2 ProgressionOrder: 0 Profile: JP2 NumberOfLayers: 1 JPEG2000Metadata: MultipleComponentTransformation: 1 Brand: jp2 NumberDecompositionLevels: 5 MinorVersion: 0 CodeBlockWidth: 4 Compatibility: jp2 CodeBlockHeight: 4 ColorspaceUnknown: true CodeBlockStyle: 0 ColorSpecs: Transformation: 0 ColorSpec: QuantizationDefault: Method: Enumerated Colorspace QuantizationStyle: 34 Precedence: 0 StepValue: 30494, 30442, 30442, 30396, 28416, 28416, 28386, Approx: 0 26444, 26444, 26468, 20483, 20483, 20549, 22482, 22482, 22369 EnumCS: sRGB NisoImageMetadata: UUIDs: MIMEType: image/jp2 UUIDBox: ByteOrder: big-endian UUID: -66, 122, -49, [...] CompressionScheme:
    [Show full text]
  • An Optimization of JPEG-LS Using an Efficient and Low-Complexity
    Received April 26th, 2021. Revised June 27th, 2021. Accepted July 23th, 2021. Digital Object Identifier 10.1109/ACCESS.2021.3100747 LOCO-ANS: An Optimization of JPEG-LS Using an Efficient and Low-Complexity Coder Based on ANS TOBÍAS ALONSO , GUSTAVO SUTTER , AND JORGE E. LÓPEZ DE VERGARA High Performance Computing and Networking Research Group, Escuela Politécnica Superior, Universidad Autónoma de Madrid, Spain. {tobias.alonso, gustavo.sutter, jorge.lopez_vergara}@uam.es This work was supported in part by the Spanish Research Agency under the project AgileMon (AEI PID2019-104451RB-C21). ABSTRACT Near-lossless compression is a generalization of lossless compression, where the codec user is able to set the maximum absolute difference (the error tolerance) between the values of an original pixel and the decoded one. This enables higher compression ratios, while still allowing the control of the bounds of the quantization errors in the space domain. This feature makes them attractive for applications where a high degree of certainty is required. The JPEG-LS lossless and near-lossless image compression standard combines a good compression ratio with a low computational complexity, which makes it very suitable for scenarios with strong restrictions, common in embedded systems. However, our analysis shows great coding efficiency improvement potential, especially for lower entropy distributions, more common in near-lossless. In this work, we propose enhancements to the JPEG-LS standard, aimed at improving its coding efficiency at a low computational overhead, particularly for hardware implementations. The main contribution is a low complexity and efficient coder, based on Tabled Asymmetric Numeral Systems (tANS), well suited for a wide range of entropy sources and with simple hardware implementation.
    [Show full text]
  • Webp - Faster Web with Smaller Images
    WebP - Faster Web with smaller images Pascal Massimino Google Confidential and Proprietary WebP New image format - Why? ● Average page size: 350KB ● Images: ~65% of Internet traffic Current image formats ● JPEG: 80% of image bytes ● PNG: mainly for alpha, lossless not always wanted ● GIF: used for animations (avatars, smileys) WebP: more efficient unified solution + extra goodies Targets Web images, not at replacing photo formats. Google Confidential and Proprietary WebP ● Unified format ○ Supports both lossy and lossless compression, with transparency ○ all-in-one replacement for JPEG, PNG and GIF ● Target: ~30% smaller images ● low-overhead container (RIFF + chunks) Google Confidential and Proprietary WebP-lossy with alpha Appealing replacement for unneeded lossless use of PNG: sprites for games, logos, page decorations ● YUV: VP8 intra-frame ● Alpha channel: WebP lossless format ● Optional pre-filtering (~10% extra compression) ● Optional quantization --> near-lossless alpha ● Compression gain: 3x compared to lossless Google Confidential and Proprietary WebP - Lossless Techniques ■ More advanced spatial predictors ■ Local palette look up ■ Cross-color de-correlation ■ Separate entropy models for R, G, B, A channels ■ Image data and metadata both are Huffman-coded Still is a very simple format, fast to decode. Google Confidential and Proprietary WebP vs PNG source: published study on developers.google.com/speed/webp Average: 25% smaller size (corpus: 1000 PNG images crawled from the web, optimized with pngcrush) Google Confidential and Proprietary Speed number (takeaway) Encoding ● Lossy (VP8): 5x slower than JPEG ● Lossless: from 2x faster to 10x slower than libpng Decoding ● Lossy (VP8): 2x-3x slower than JPEG ● Lossless: ~1.5x faster than libpng Decoder's goodies: ● Incremental ● Per-row output (very low memory footprint) ● on-the-fly rescaling and cropping (e.g.
    [Show full text]