How to Exploit the Transferability of Learned Image Compression to Conventional Codecs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Free Lossless Image Format
FREE LOSSLESS IMAGE FORMAT Jon Sneyers and Pieter Wuille [email protected] [email protected] Cloudinary Blockstream ICIP 2016, September 26th DON’T WE HAVE ENOUGH IMAGE FORMATS ALREADY? • JPEG, PNG, GIF, WebP, JPEG 2000, JPEG XR, JPEG-LS, JBIG(2), APNG, MNG, BPG, TIFF, BMP, TGA, PCX, PBM/PGM/PPM, PAM, … • Obligatory XKCD comic: YES, BUT… • There are many kinds of images: photographs, medical images, diagrams, plots, maps, line art, paintings, comics, logos, game graphics, textures, rendered scenes, scanned documents, screenshots, … EVERYTHING SUCKS AT SOMETHING • None of the existing formats works well on all kinds of images. • JPEG / JP2 / JXR is great for photographs, but… • PNG / GIF is great for line art, but… • WebP: basically two totally different formats • Lossy WebP: somewhat better than (moz)JPEG • Lossless WebP: somewhat better than PNG • They are both .webp, but you still have to pick the format GOAL: ONE FORMAT THAT COMPRESSES ALL IMAGES WELL EXPERIMENTAL RESULTS Corpus Lossless formats JPEG* (bit depth) FLIF FLIF* WebP BPG PNG PNG* JP2* JXR JLS 100% 90% interlaced PNGs, we used OptiPNG [21]. For BPG we used [4] 8 1.002 1.000 1.234 1.318 1.480 2.108 1.253 1.676 1.242 1.054 0.302 the options -m 9 -e jctvc; for WebP we used -m 6 -q [4] 16 1.017 1.000 / / 1.414 1.502 1.012 2.011 1.111 / / 100. For the other formats we used default lossless options. [5] 8 1.032 1.000 1.099 1.163 1.429 1.664 1.097 1.248 1.500 1.017 0.302� [6] 8 1.003 1.000 1.040 1.081 1.282 1.441 1.074 1.168 1.225 0.980 0.263 Figure 4 shows the results; see [22] for more details. -

Chapter 9 Image Compression Standards
Fundamentals of Multimedia, Chapter 9 Chapter 9 Image Compression Standards 9.1 The JPEG Standard 9.2 The JPEG2000 Standard 9.3 The JPEG-LS Standard 9.4 Bi-level Image Compression Standards 9.5 Further Exploration 1 Li & Drew c Prentice Hall 2003 ! Fundamentals of Multimedia, Chapter 9 9.1 The JPEG Standard JPEG is an image compression standard that was developed • by the “Joint Photographic Experts Group”. JPEG was for- mally accepted as an international standard in 1992. JPEG is a lossy image compression method. It employs a • transform coding method using the DCT (Discrete Cosine Transform). An image is a function of i and j (or conventionally x and y) • in the spatial domain. The 2D DCT is used as one step in JPEG in order to yield a frequency response which is a function F (u, v) in the spatial frequency domain, indexed by two integers u and v. 2 Li & Drew c Prentice Hall 2003 ! Fundamentals of Multimedia, Chapter 9 Observations for JPEG Image Compression The effectiveness of the DCT transform coding method in • JPEG relies on 3 major observations: Observation 1: Useful image contents change relatively slowly across the image, i.e., it is unusual for intensity values to vary widely several times in a small area, for example, within an 8 8 × image block. much of the information in an image is repeated, hence “spa- • tial redundancy”. 3 Li & Drew c Prentice Hall 2003 ! Fundamentals of Multimedia, Chapter 9 Observations for JPEG Image Compression (cont’d) Observation 2: Psychophysical experiments suggest that hu- mans are much less likely to notice the loss of very high spatial frequency components than the loss of lower frequency compo- nents. -

Download This PDF File
Sindh Univ. Res. Jour. (Sci. Ser.) Vol.47 (3) 531-534 (2015) I NDH NIVERSITY ESEARCH OURNAL ( CIENCE ERIES) S U R J S S Performance Analysis of Image Compression Standards with Reference to JPEG 2000 N. MINALLAH++, A. KHALIL, M. YOUNAS, M. FURQAN, M. M. BOKHARI Department of Computer Systems Engineering, University of Engineering and Technology, Peshawar Received 12thJune 2014 and Revised 8th September 2015 Abstract: JPEG 2000 is the most widely used standard for still image coding. Some other well-known image coding techniques include JPEG, JPEG XR and WEBP. This paper provides performance evaluation of JPEG 2000 with reference to other image coding standards, such as JPEG, JPEG XR and WEBP. For the performance evaluation of JPEG 2000 with reference to JPEG, JPEG XR and WebP, we considered divers image coding scenarios such as continuous tome images, grey scale images, High Definition (HD) images, true color images and web images. Each of the considered algorithms are briefly explained followed by their performance evaluation using different quality metrics, such as Peak Signal to Noise Ratio (PSNR), Mean Square Error (MSE), Structure Similarity Index (SSIM), Bits Per Pixel (BPP), Compression Ratio (CR) and Encoding/ Decoding Complexity. The results obtained showed that choice of the each algorithm depends upon the imaging scenario and it was found that JPEG 2000 supports the widest set of features among the evaluated standards and better performance. Keywords: Analysis, Standards JPEG 2000. performance analysis, followed by Section 6 with 1. INTRODUCTION There are different standards of image compression explanation of the considered performance analysis and decompression. -

Image Compression Using Discrete Cosine Transform Method
Qusay Kanaan Kadhim, International Journal of Computer Science and Mobile Computing, Vol.5 Issue.9, September- 2016, pg. 186-192 Available Online at www.ijcsmc.com International Journal of Computer Science and Mobile Computing A Monthly Journal of Computer Science and Information Technology ISSN 2320–088X IMPACT FACTOR: 5.258 IJCSMC, Vol. 5, Issue. 9, September 2016, pg.186 – 192 Image Compression Using Discrete Cosine Transform Method Qusay Kanaan Kadhim Al-Yarmook University College / Computer Science Department, Iraq [email protected] ABSTRACT: The processing of digital images took a wide importance in the knowledge field in the last decades ago due to the rapid development in the communication techniques and the need to find and develop methods assist in enhancing and exploiting the image information. The field of digital images compression becomes an important field of digital images processing fields due to the need to exploit the available storage space as much as possible and reduce the time required to transmit the image. Baseline JPEG Standard technique is used in compression of images with 8-bit color depth. Basically, this scheme consists of seven operations which are the sampling, the partitioning, the transform, the quantization, the entropy coding and Huffman coding. First, the sampling process is used to reduce the size of the image and the number bits required to represent it. Next, the partitioning process is applied to the image to get (8×8) image block. Then, the discrete cosine transform is used to transform the image block data from spatial domain to frequency domain to make the data easy to process. -

Neural Multi-Scale Image Compression
Neural Multi-scale Image Compression Ken Nakanishi 1 Shin-ichi Maeda 2 Takeru Miyato 2 Daisuke Okanohara 2 Abstract 1.00 This study presents a new lossy image compres- sion method that utilizes the multi-scale features 0.98 of natural images. Our model consists of two networks: multi-scale lossy autoencoder and par- 0.96 allel multi-scale lossless coder. The multi-scale Proposed 0.94 JPEG lossy autoencoder extracts the multi-scale image MS-SSIM WebP features to quantized variables and the parallel BPG 0.92 multi-scale lossless coder enables rapid and ac- Johnston et al. Rippel & Bourdev curate lossless coding of the quantized variables 0.90 via encoding/decoding the variables in parallel. 0.0 0.2 0.4 0.6 0.8 1.0 Our proposed model achieves comparable perfor- Bits per pixel mance to the state-of-the-art model on Kodak and RAISE-1k dataset images, and it encodes a PNG image of size 768 × 512 in 70 ms with a single Figure 1. Rate-distortion trade off curves with different methods GPU and a single CPU process and decodes it on Kodak dataset. The horizontal axis represents bits-per-pixel into a high-fidelity image in approximately 200 (bpp) and the vertical axis represents multi-scale structural similar- ms. ity (MS-SSIM). Our model achieves better or comparable bpp with respect to the state-of-the-art results (Rippel & Bourdev, 2017). 1. Introduction K Data compression for video and image data is a crucial tech- via ML algorithm is not new. The -means algorithm was nique for reducing communication traffic and saving data used for vector quantization (Gersho & Gray, 2012), and storage. -

Task-Aware Quantization Network for JPEG Image Compression
Task-Aware Quantization Network for JPEG Image Compression Jinyoung Choi1 and Bohyung Han1 Dept. of ECE & ASRI, Seoul National University, Korea fjin0.choi,[email protected] Abstract. We propose to learn a deep neural network for JPEG im- age compression, which predicts image-specific optimized quantization tables fully compatible with the standard JPEG encoder and decoder. Moreover, our approach provides the capability to learn task-specific quantization tables in a principled way by adjusting the objective func- tion of the network. The main challenge to realize this idea is that there exist non-differentiable components in the encoder such as run-length encoding and Huffman coding and it is not straightforward to predict the probability distribution of the quantized image representations. We address these issues by learning a differentiable loss function that approx- imates bitrates using simple network blocks|two MLPs and an LSTM. We evaluate the proposed algorithm using multiple task-specific losses| two for semantic image understanding and another two for conventional image compression|and demonstrate the effectiveness of our approach to the individual tasks. Keywords: JPEG image compression, adaptive quantization, bitrate approximation. 1 Introduction Image compression is a classical task to reduce the file size of an input image while minimizing the loss of visual quality. This task has two categories|lossy and lossless compression. Lossless compression algorithms preserve the contents of input images perfectly even after compression, but their compression rates are typically low. On the other hand, lossy compression techniques allow the degra- dation of the original images by quantization and reduce the file size significantly compared to lossless counterparts. -
![Arxiv:2002.01657V1 [Eess.IV] 5 Feb 2020 Port Lossless Model to Compress Images Lossless](https://docslib.b-cdn.net/cover/2332/arxiv-2002-01657v1-eess-iv-5-feb-2020-port-lossless-model-to-compress-images-lossless-882332.webp)
Arxiv:2002.01657V1 [Eess.IV] 5 Feb 2020 Port Lossless Model to Compress Images Lossless
LEARNED LOSSLESS IMAGE COMPRESSION WITH A HYPERPRIOR AND DISCRETIZED GAUSSIAN MIXTURE LIKELIHOODS Zhengxue Cheng, Heming Sun, Masaru Takeuchi, Jiro Katto Department of Computer Science and Communications Engineering, Waseda University, Tokyo, Japan. ABSTRACT effectively in [12, 13, 14]. Some methods decorrelate each Lossless image compression is an important task in the field channel of latent codes and apply deep residual learning to of multimedia communication. Traditional image codecs improve the performance as [15, 16, 17]. However, deep typically support lossless mode, such as WebP, JPEG2000, learning based lossless compression has rarely discussed. FLIF. Recently, deep learning based approaches have started One related work is L3C [18] to propose a hierarchical archi- to show the potential at this point. HyperPrior is an effective tecture with 3 scales to compress images lossless. technique proposed for lossy image compression. This paper In this paper, we propose a learned lossless image com- generalizes the hyperprior from lossy model to lossless com- pression using a hyperprior and discretized Gaussian mixture pression, and proposes a L2-norm term into the loss function likelihoods. Our contributions mainly consist of two aspects. to speed up training procedure. Besides, this paper also in- First, we generalize the hyperprior from lossy model to loss- vestigated different parameterized models for latent codes, less compression model, and propose a loss function with L2- and propose to use Gaussian mixture likelihoods to achieve norm for lossless compression to speed up training. Second, adaptive and flexible context models. Experimental results we investigate four parameterized distributions and propose validate our method can outperform existing deep learning to use Gaussian mixture likelihoods for the context model. -

Image Formats
Image Formats Ioannis Rekleitis Many different file formats • JPEG/JFIF • Exif • JPEG 2000 • BMP • GIF • WebP • PNG • HDR raster formats • TIFF • HEIF • PPM, PGM, PBM, • BAT and PNM • BPG CSCE 590: Introduction to Image Processing https://en.wikipedia.org/wiki/Image_file_formats 2 Many different file formats • JPEG/JFIF (Joint Photographic Experts Group) is a lossy compression method; JPEG- compressed images are usually stored in the JFIF (JPEG File Interchange Format) >ile format. The JPEG/JFIF >ilename extension is JPG or JPEG. Nearly every digital camera can save images in the JPEG/JFIF format, which supports eight-bit grayscale images and 24-bit color images (eight bits each for red, green, and blue). JPEG applies lossy compression to images, which can result in a signi>icant reduction of the >ile size. Applications can determine the degree of compression to apply, and the amount of compression affects the visual quality of the result. When not too great, the compression does not noticeably affect or detract from the image's quality, but JPEG iles suffer generational degradation when repeatedly edited and saved. (JPEG also provides lossless image storage, but the lossless version is not widely supported.) • JPEG 2000 is a compression standard enabling both lossless and lossy storage. The compression methods used are different from the ones in standard JFIF/JPEG; they improve quality and compression ratios, but also require more computational power to process. JPEG 2000 also adds features that are missing in JPEG. It is not nearly as common as JPEG, but it is used currently in professional movie editing and distribution (some digital cinemas, for example, use JPEG 2000 for individual movie frames). -

Why Compression Matters
Computational thinking for digital technologies: Snapshot 2 PROGRESS OUTCOME 6 Why compression matters Context Sarah has been investigating the concept of compression coding, by looking at the different ways images can be compressed and the trade-offs of using different methods of compression in relation to the size and quality of images. She researches the topic by doing several web searches and produces a report with her findings. Insight 1: Reasons for compressing files I realised that data compression is extremely useful as it reduces the amount of space needed to store files. Computers and storage devices have limited space, so using smaller files allows you to store more files. Compressed files also download more quickly, which saves time – and money, because you pay less for electricity and bandwidth. Compression is also important in terms of HCI (human-computer interaction), because if images or videos are not compressed they take longer to download and, rather than waiting, many users will move on to another website. Insight 2: Representing images in an uncompressed form Most people don’t realise that a computer image is made up of tiny dots of colour, called pixels (short for “picture elements”). Each pixel has components of red, green and blue light and is represented by a binary number. The more bits used to represent each component, the greater the depth of colour in your image. For example, if red is represented by 8 bits, green by 8 bits and blue by 8 bits, 16,777,216 different colours can be represented, as shown below: 8 bits corresponds to 256 possible numbers in binary red x green x blue = 256 x 256 x 256 = 16,777,216 possible colour combinations 1 Insight 3: Lossy compression and human perception There are many different formats for file compression such as JPEG (image compression), MP3 (audio compression) and MPEG (audio and video compression). -

Comparison of JPEG's Competitors for Document Images
Comparison of JPEG’s competitors for document images Mostafa Darwiche1, The-Anh Pham1 and Mathieu Delalandre1 1 Laboratoire d’Informatique, 64 Avenue Jean Portalis, 37200 Tours, France e-mail: fi[email protected] Abstract— In this work, we carry out a study on the per- in [6] concerns assessing quality of common image formats formance of potential JPEG’s competitors when applied to (e.g., JPEG, TIFF, and PNG) that relies on optical charac- document images. Many novel codecs, such as BPG, Mozjpeg, ter recognition (OCR) errors and peak signal to noise ratio WebP and JPEG-XR, have been recently introduced in order to substitute the standard JPEG. Nonetheless, there is a lack of (PSNR) metric. The authors in [3] compare the performance performance evaluation of these codecs, especially for a particular of different coding methods (JPEG, JPEG 2000, MRC) using category of document images. Therefore, this work makes an traditional PSNR metric applied to several document samples. attempt to provide a detailed and thorough analysis of the Since our target is to provide a study on document images, aforementioned JPEG’s competitors. To this aim, we first provide we then use a large dataset with different image resolutions, a review of the most famous codecs that have been considered as being JPEG replacements. Next, some experiments are performed compress them at very low bit-rate and after that evaluate the to study the behavior of these coding schemes. Finally, we extract output images using OCR accuracy. We also take into account main remarks and conclusions characterizing the performance the PSNR measure to serve as an additional quality metric. -

Video Compression and Communications: from Basics to H.261, H.263, H.264, MPEG2, MPEG4 for DVB and HSDPA-Style Adaptive Turbo-Transceivers
Video Compression and Communications: From Basics to H.261, H.263, H.264, MPEG2, MPEG4 for DVB and HSDPA-Style Adaptive Turbo-Transceivers by c L. Hanzo, P.J. Cherriman, J. Streit Department of Electronics and Computer Science, University of Southampton, UK About the Authors Lajos Hanzo (http://www-mobile.ecs.soton.ac.uk) FREng, FIEEE, FIET, DSc received his degree in electronics in 1976 and his doctorate in 1983. During his 30-year career in telecommunications he has held various research and academic posts in Hungary, Germany and the UK. Since 1986 he has been with the School of Electronics and Computer Science, University of Southampton, UK, where he holds the chair in telecom- munications. He has co-authored 15 books on mobile radio communica- tions totalling in excess of 10 000, published about 700 research papers, acted as TPC Chair of IEEE conferences, presented keynote lectures and been awarded a number of distinctions. Currently he is directing an academic research team, working on a range of research projects in the field of wireless multimedia communications sponsored by industry, the Engineering and Physical Sciences Research Council (EPSRC) UK, the European IST Programme and the Mobile Virtual Centre of Excellence (VCE), UK. He is an enthusiastic supporter of industrial and academic liaison and he offers a range of industrial courses. He is also an IEEE Distinguished Lecturer of both the Communications Society and the Vehicular Technology Society (VTS). Since 2005 he has been a Governer of the VTS. For further information on research in progress and associated publications please refer to http://www-mobile.ecs.soton.ac.uk Peter J. -
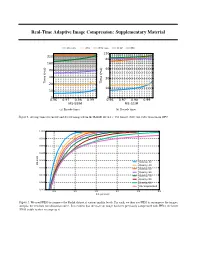
Real-Time Adaptive Image Compression: Supplementary Material
Real-Time Adaptive Image Compression: Supplementary Material WaveOne JPEG JPEG 2000 WebP BPG 120 320 80 160 80 40 40 20 Time (ms) 20 Time (ms) 10 10 5 5 0.96 0.97 0.98 0.99 0.96 0.97 0.98 0.99 MS-SSIM MS-SSIM (a) Encode times. (b) Decode times. Figure 1. Average times to encode and decode images from the RAISE-1k 512 × 768 dataset. Note our codec was run on GPU. 1.000 0.995 0.990 0.985 0.980 Quality 30 MS-SSIM Quality 40 0.975 Quality 50 Quality 60 0.970 Quality 70 Quality 80 0.965 Quality 90 Uncompressed 0.960 0.5 1.0 1.5 2.0 2.5 3.0 Bits per pixel Figure 2. We used JPEG to compress the Kodak dataset at various quality levels. For each, we then use JPEG to recompress the images, and plot the resultant rate-distortion curve. It is evident that the more an image has been previously compressed with JPEG, the better JPEG is able to then recompress it. information across different scales. In SectionWe 4 average of these the to main attain textreconstruction. we the We discuss accumulate final the scalar value motivation outputs for along providedtargets these branches to and architectural constructed the choices along the the in reconstructions. objective processing more sigmoid pipeline, The detail. Figure function. branched goal 3. out of at This the different multiscale depths. discriminator architecture is allows to aggregating infer which of the two inputs is then the real target, and which is its Target The architecture of the discriminator used in our adversarial training procedure.