New Stellar Encounters Discovered in the Second Gaia Data Release C.A.L
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Naming the Extrasolar Planets
Naming the extrasolar planets W. Lyra Max Planck Institute for Astronomy, K¨onigstuhl 17, 69177, Heidelberg, Germany [email protected] Abstract and OGLE-TR-182 b, which does not help educators convey the message that these planets are quite similar to Jupiter. Extrasolar planets are not named and are referred to only In stark contrast, the sentence“planet Apollo is a gas giant by their assigned scientific designation. The reason given like Jupiter” is heavily - yet invisibly - coated with Coper- by the IAU to not name the planets is that it is consid- nicanism. ered impractical as planets are expected to be common. I One reason given by the IAU for not considering naming advance some reasons as to why this logic is flawed, and sug- the extrasolar planets is that it is a task deemed impractical. gest names for the 403 extrasolar planet candidates known One source is quoted as having said “if planets are found to as of Oct 2009. The names follow a scheme of association occur very frequently in the Universe, a system of individual with the constellation that the host star pertains to, and names for planets might well rapidly be found equally im- therefore are mostly drawn from Roman-Greek mythology. practicable as it is for stars, as planet discoveries progress.” Other mythologies may also be used given that a suitable 1. This leads to a second argument. It is indeed impractical association is established. to name all stars. But some stars are named nonetheless. In fact, all other classes of astronomical bodies are named. -

19 6 6Apj. . .14 6. .743D the VARIABILITY of RHO PUPPIS* I. J
.743D 6. .14 THE VARIABILITY OF RHO PUPPIS* . I. J. Danziger and L. V. Kumf 6ApJ. Mount Wilson and Palomar Observatories 6 19 Carnegie Institution of Washington, California Institute of Technology Received April 30, 1966 ABSTRACT The results of simultaneous spectrophotometric and spectral observations of the short-period variable star, p Puppis, are reported. The amplitudes of radial-velocity, light, and temperature variations are 11 km/sec, 0.15 mag., and 280° K, respectively. The relative phases differ from those observed in cluster- type c variables. Estimates of the absolute luminosity and mass from the observed gravity and the Py/(p/po) — Q relationship indicate that either p Puppis is pulsating in a higher-order harmonic mode than the first or the theory of its pulsation is not understood. I. INTRODUCTION The bright star p Puppis, classified in the MKK system as type F6II, was first shown to be variable in light (period 0.141 days) by Eggen (1956) who measured a total ampli- tude of 0.15 mag. Struve, Sahade, and Zebergs (1956) showed that there is an associated variation in radial velocity with a total amplitude of 10 km/sec and that maximum brightness occurs approximately 0.02 days later than minimum radial velocity. Bappu (1959) reported that two-color measurements indicate a variation in temperature of 300° K. An intrinsic luminosity of p Puppis, MPg = +2.4, was obtained by Kinman (1959). He assumed it fitted the observed period-luminosity relation of cluster-type c variables in order to use an observed period-luminosity relation. Strömgren’s c-l sys- tem indices were measured by McNamara and Augason (1962) to derive Mpg = +1.7 and a mass 9J£ = 3.2 $)îo from the period-density law with the pulsation constant Q ~ 0-041* It is of interest to note that, although p Puppis has been classified as a ô Scuti star, none of the multiple-period characteristics associated with such stars has been found to apply to it. -
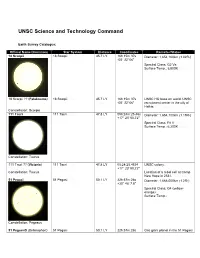
UNSC Science and Technology Command
UNSC Science and Technology Command Earth Survey Catalogue: Official Name/(Common) Star System Distance Coordinates Remarks/Status 18 Scorpii {TCP:p351} 18 Scorpii {Fact} 45.7 LY 16h 15m 37s Diameter: 1,654,100km (1.02R*) {Fact} -08° 22' 06" {Fact} Spectral Class: G2 Va {Fact} Surface Temp.: 5,800K {Fact} 18 Scorpii ?? (Falaknuma) 18 Scorpii {Fact} 45.7 LY 16h 15m 37s UNSC HQ base on world. UNSC {TCP:p351} {Fact} -08° 22' 06" recruitment center in the city of Halkia. {TCP:p355} Constellation: Scorpio 111 Tauri 111 Tauri {Fact} 47.8 LY 05h:24m:25.46s Diameter: 1,654,100km (1.19R*) {Fact} +17° 23' 00.72" {Fact} Spectral Class: F8 V {Fact} Surface Temp.: 6,200K {Fact} Constellation: Taurus 111 Tauri ?? (Victoria) 111 Tauri {Fact} 47.8 LY 05:24:25.4634 UNSC colony. {GoO:p31} {Fact} +17° 23' 00.72" Constellation: Taurus Location of a rebel cell at Camp New Hope in 2531. {GoO:p31} 51 Pegasi {Fact} 51 Pegasi {Fact} 50.1 LY 22h:57m:28s Diameter: 1,668,000km (1.2R*) {Fact} +20° 46' 7.8" {Fact} Spectral Class: G4 (yellow- orange) {Fact} Surface Temp.: Constellation: Pegasus 51 Pegasi-B (Bellerophon) 51 Pegasi 50.1 LY 22h:57m:28s Gas giant planet in the 51 Pegasi {Fact} +20° 46' 7.8" system informally named Bellerophon. Diameter: 196,000km. {Fact} Located on the edge of UNSC territory. {GoO:p15} Its moon, Pegasi Delta, contained a Covenant deuterium/tritium refinery destroyed by covert UNSC forces in 2545. {GoO:p13} Constellation: Pegasus 51 Pegasi-B-1 (Pegasi 51 Pegasi 50.1 LY 22h:57m:28s Moon of the gas giant planet 51 Delta) {GoO:p13} +20° 46' 7.8" Pegasi-B in the 51 Pegasi star Constellation: Pegasus system; a Covenant stronghold on the edge of UNSC territory. -

The Electric Sun Hypothesis
Basics of astrophysics revisited. II. Mass- luminosity- rotation relation for F, A, B, O and WR class stars Edgars Alksnis [email protected] Small volume statistics show, that luminosity of bright stars is proportional to their angular momentums of rotation when certain relation between stellar mass and stellar rotation speed is reached. Cause should be outside of standard stellar model. Concept allows strengthen hypotheses of 1) fast rotation of Wolf-Rayet stars and 2) low mass central black hole of the Milky Way. Keywords: mass-luminosity relation, stellar rotation, Wolf-Rayet stars, stellar angular momentum, Sagittarius A* mass, Sagittarius A* luminosity. In previous work (Alksnis, 2017) we have shown, that in slow rotating stars stellar luminosity is proportional to spin angular momentum of the star. This allows us to see, that there in fact are no stars outside of “main sequence” within stellar classes G, K and M. METHOD We have analyzed possible connection between stellar luminosity and stellar angular momentum in samples of most known F, A, B, O and WR class stars (tables 1-5). Stellar equatorial rotation speed (vsini) was used as main parameter of stellar rotation when possible. Several diverse data for one star were averaged. Zero stellar rotation speed was considered as an error and corresponding star has been not included in sample. RESULTS 2 F class star Relative Relative Luminosity, Relative M*R *eq mass, M radius, L rotation, L R eq HATP-6 1.29 1.46 3.55 2.950 2.28 α UMi B 1.39 1.38 3.90 38.573 26.18 Alpha Fornacis 1.33 -
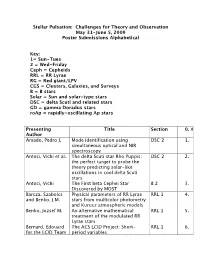
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical Key: 1= Sun-Tues 2 = Wed-Friday Ceph = Cepheids RRL = RR Lyrae RG = Red giant/LPV CGS = Clusters, Galaxies, and Surveys B = B stars Solar = Sun and solar-type stars DSC = delta Scuti and related stars GD = gamma Doradus stars roAp = rapidly-oscillating Ap stars Presenting Title Section 0. # Author Amado, Pedro J. Mode identification using DSC 2 1. simultaneous optical and NIR spectroscopy Antoci, Vichi et al. The delta Scuti star Rho Puppis: DSC 2 2. the perfect target to probe the theory predicting solar-like oscillations in cool delta Scuti stars Antoci, Vichi The First beta Cephei Star B 2 3. Discovered by MOST Barcza, Szabolcs Physical parameters of RR Lyrae RRL 1 4. and Benko, J.M. stars from multicolor photometry and Kurucz atmospheric models Benko, Jozsef M. An alternative mathematical RRL 1 5. treatment of the modulated RR Lyrae stars Bernard, Edouard The ACS LCID Project: Short- RRL 1 6. for the LCID Team period variables Bersier, David et A large-scale survey for variable CGS 1 7. al. stars in M33 Bouabid, Mehdi- Frequency analysis of the SISMO GD 2 8. Pierre $\gamma$Doradus star HD 49434 Bouabid, Mehdi- Hybrid GD 2 9. Pierre $\gamma$Doradus/$\delta$Scuti stars: theory versus observations Breger, M., Lenz, Is 44 Tau in the post-MS DS 2 10. Patrick, and contraction phase? Pamyatnykh, A. Cameron, Chris et Asteroseismic tuning of the roAp 2 11. al. magnetic field of the roAp star HR 1217 Cameron, Chris et Near-critical rotation offers the B 2 12. -

The Astrology of Space
The Astrology of Space 1 The Astrology of Space The Astrology Of Space By Michael Erlewine 2 The Astrology of Space An ebook from Startypes.com 315 Marion Avenue Big Rapids, Michigan 49307 Fist published 2006 © 2006 Michael Erlewine/StarTypes.com ISBN 978-0-9794970-8-7 All rights reserved. No part of the publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of the publisher. Graphics designed by Michael Erlewine Some graphic elements © 2007JupiterImages Corp. Some Photos Courtesy of NASA/JPL-Caltech 3 The Astrology of Space This book is dedicated to Charles A. Jayne And also to: Dr. Theodor Landscheidt John D. Kraus 4 The Astrology of Space Table of Contents Table of Contents ..................................................... 5 Chapter 1: Introduction .......................................... 15 Astrophysics for Astrologers .................................. 17 Astrophysics for Astrologers .................................. 22 Interpreting Deep Space Points ............................. 25 Part II: The Radio Sky ............................................ 34 The Earth's Aura .................................................... 38 The Kinds of Celestial Light ................................... 39 The Types of Light ................................................. 41 Radio Frequencies ................................................. 43 Higher Frequencies ............................................... -

Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Presenting Author Title 0. # Amado, Pedro J. Mode identification using 1. simultaneous optical and NIR spectroscopy Ando, Hiroyasu et Detection of Solar-like Oscillations 2. al. in 4 G-giants by precise radial velocity measurement and their characteristics Antoci, Vichi et al. The delta Scuti star Rho Puppis: 3. the perfect target to probe the theory predicting solar-like oscillations in cool delta Scuti stars Barcza, Szabolcs and Physical parameters of RR Lyrae 4. Benko, J.M. stars from multicolor photometry and Kurucz atmospheric models Benko, Jozsef M. An alternative mathematical 5. treatment of the modulated RR Lyrae stars Bernard, Edouard for The ACS LCID Project: Short- 6. the LCID Team period variables Bouabid, Mehdi- Frequency analysis of the SISMO 7. Pierre $\gamma$Doradus star HD 49434 Bouabid, Mehdi- Hybrid 8. Pierre $\gamma$Doradus/$\delta$Scuti stars: theory versus observations Cameron, Chris et Asteroseismic tuning of the 9. al. magnetic field of the roAp star HR 1217 Cameron, Chris et Near-critical rotation offers the 10. al. MOST asteroseismic potential Cash, Jennifer et al. A Long Term Photometric and 11. Spectroscopic Study of RV Tauri stars Chadid, Merieme et First light curves from Antarctica: 12. al. PAIX monitoring of the Blazhko stars Chavez, Joy M. et al. A Cepheid Distance to the 13. Antennae De Cat, Peter et al. Is HD147787 a double-lined 14. binary with two pulsating components? De Cat, Peter et al. Towards asteroseismology of 15. main-sequence g-mode pulsators: spectroscopic multi- site campaigns for slowly pulsating B stars and gamma Doradus stars. -

Curriculum Vitae Date: 4/03/2013 Initials
Curriculum Vitae Date: 4/03/2013 Initials: Gordon Arthur Hunter WALKER Born: 30 January 1936 Married: Sigrid Helene Fischer, April 1962 Children: Nicholas and Eric Languages: English, French, and German. POST-SECONDARY EDUCATION University of Edinburgh Hon.B.Sc. Natural Philosophy 1958 University of Cambridge (Caius) Ph.D. Astrophysics 1962 PROFESSIONAL EMPLOYMENT Radcliffe Observatory, Pretoria Research Assistant 1960-61 DAO, Victoria NRC Fellow 1962-63 DAO, Victoria Scientific Officer 3 1963-69 University of Texas Visiting Lecturer 1965 (Spring) University of Victoria Visiting Lecturer 1966 (Spring) UBC Associate Professor April 1, 1969 Director, Institute 1972-78 Astronomy and Space Science Professor July 1, 1974-97 Professor Emeritus July 1 1997 { HIA/NRC Guest-worker 1998 { UVic Adjunct Professor April 23 2004 { INTERNATIONAL PROJECTS Scientific Advisory Committee of the CFHT 1972-79 Project Scientist for `Starlab' an Australian, Canadian, NASA, space telescope proposal until Canada withdrew in 1984 CFHT Board of Directors 1986-91 Canadian Project Scientist (1989-90): EUVITA - far ultraviolet astronomical satellite experiment joint with USSR, Switzerland, USA. Canadian Project Scientist (1990{97): Gemini - twin 8 metre optical telescopes (1 in Hawaii, 1 in Chile) joint with USA, U.K., Chile, Australia, Argentina, Brazil. Gemini Scientific Advisory Committee 1991{97 Gemini Board of Directors 1991{97 1 MOST Science team (1997{2009): a Canadian satellite launched in 2003 for ultra-precise photom- etry of bright stars, with collaboration from Austria. Gemini/NSF Visiting Committee 2004 AURA Source Selection Board for future Gemini Instrumentation 2004 TMT - chair HROS Review Panel 2005 chair Gemini Source Selection Board for HRNIRS 2005 chair Gemini Source Selection Board for PRVS 2006 member SPIRou Preliminary Design Revue Committee 2012 - a high resolution visible/infrared spectropolarimeter proposed for CFHT RESEARCH CAREER My fascination with astronomy began at age 7 when my father explained that stars were very distant suns. -

The Universe Contents 3 HD 149026 B
History . 64 Antarctica . 136 Utopia Planitia . 209 Umbriel . 286 Comets . 338 In Popular Culture . 66 Great Barrier Reef . 138 Vastitas Borealis . 210 Oberon . 287 Borrelly . 340 The Amazon Rainforest . 140 Titania . 288 C/1861 G1 Thatcher . 341 Universe Mercury . 68 Ngorongoro Conservation Jupiter . 212 Shepherd Moons . 289 Churyamov- Orientation . 72 Area . 142 Orientation . 216 Gerasimenko . 342 Contents Magnetosphere . 73 Great Wall of China . 144 Atmosphere . .217 Neptune . 290 Hale-Bopp . 343 History . 74 History . 218 Orientation . 294 y Halle . 344 BepiColombo Mission . 76 The Moon . 146 Great Red Spot . 222 Magnetosphere . 295 Hartley 2 . 345 In Popular Culture . 77 Orientation . 150 Ring System . 224 History . 296 ONIS . 346 Caloris Planitia . 79 History . 152 Surface . 225 In Popular Culture . 299 ’Oumuamua . 347 In Popular Culture . 156 Shoemaker-Levy 9 . 348 Foreword . 6 Pantheon Fossae . 80 Clouds . 226 Surface/Atmosphere 301 Raditladi Basin . 81 Apollo 11 . 158 Oceans . 227 s Ring . 302 Swift-Tuttle . 349 Orbital Gateway . 160 Tempel 1 . 350 Introduction to the Rachmaninoff Crater . 82 Magnetosphere . 228 Proteus . 303 Universe . 8 Caloris Montes . 83 Lunar Eclipses . .161 Juno Mission . 230 Triton . 304 Tempel-Tuttle . 351 Scale of the Universe . 10 Sea of Tranquility . 163 Io . 232 Nereid . 306 Wild 2 . 352 Modern Observing Venus . 84 South Pole-Aitken Europa . 234 Other Moons . 308 Crater . 164 Methods . .12 Orientation . 88 Ganymede . 236 Oort Cloud . 353 Copernicus Crater . 165 Today’s Telescopes . 14. Atmosphere . 90 Callisto . 238 Non-Planetary Solar System Montes Apenninus . 166 How to Use This Book 16 History . 91 Objects . 310 Exoplanets . 354 Oceanus Procellarum .167 Naming Conventions . 18 In Popular Culture . -

New Stellar Encounters Discovered in the Second Gaia Data Release?
A&A 616, A37 (2018) https://doi.org/10.1051/0004-6361/201833456 Astronomy c ESO 2018 & Astrophysics New stellar encounters discovered in the second Gaia data release? C. A. L. Bailer-Jones, J. Rybizki, R. Andrae, and M. Fouesneau Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany e-mail: [email protected] Received 19 May 2018 / Accepted 19 June 2018 ABSTRACT Passing stars may play an important role in the evolution of our solar system. We search for close stellar encounters to the Sun among all 7.2 million stars in Gaia DR2 that have six-dimensional phase space data. We characterize encounters by integrating their orbits through a Galactic potential and propagating the correlated uncertainties via a Monte Carlo resampling. After filtering to remove spurious data, we find 694 stars that have median (over uncertainties) closest encounter distances within 5 pc, all occurring within 15 Myr from now. 26 of these have at least a 50% chance of coming closer than 1 pc (and 7 within 0.5 pc), all but one of which are newly discovered here. We confirm some and refute several other previously-identified encounters, confirming suspicions about their data. The closest encounter in the sample is Gl 710, which has a 95% probability of coming closer than 0.08 pc (17 000 AU). Taking mass estimates obtained from Gaia astrometry and multiband photometry for essentially all encounters, we find that Gl 710 also has the largest impulse on the Oort cloud. Using a Galaxy model, we compute the completeness of the Gaia DR2 encountering sample as a function of perihelion time and distance. -

STARS2016: Understanding the Roles of Rotation, Pulsation and Chemical Peculiarities in the Upper Main Sequence
i “STARS2016˙abstbook˙a4” — 2016/9/11 — 23:40 — page i — #1 i i i STARS2016: Understanding the roles of rotation, pulsation and chemical peculiarities in the upper main sequence 11 – 16 September 2016 Low Wood Bay Hotel, Lake District, UK i i i i i “STARS2016˙abstbook˙a4” — 2016/9/11 — 23:40 — page 1 — #2 i i i 11 – 16 September 2016, Low Wood Bay Hotel Contents Introduction 3 Delegate List 13 Timetable 19 Talks 27 Monday: 12th September . 29 Tuesday: 13th September . 43 Wednesday: 14th September . 55 Thursday: 15th September . 63 Friday: 16th September . 79 Posters 85 Poster abstracts: . 89 Notes 101 1 i i i i STARS2016 2 i “STARS2016˙abstbook˙a4” — 2016/9/11 — 23:40 — page 3 — #3 i i i 11 – 16 September 2016, Low Wood Bay Hotel STARS2016: Understanding the roles of rotation, pulsation and chemical peculiarities in the upper main sequence Introduction 3 i i i i STARS2016 4 i “STARS2016˙abstbook˙a4” — 2016/9/11 — 23:40 — page 5 — #4 i i i 11 – 16 September 2016, Low Wood Bay Hotel Scientific Rationale A complex relationship exists between rotation, binarity, pulsation, magnetism and chemical peculiarity in upper main sequence stars. In the region of the HR diagram where the classical instability strip crosses the main sequence, one finds the delta Scuti and gamma Doradus stars, alongside the strongly magnetic roAp stars. Pulsational variability is also observed in evolved stars such as the RR Lyrae and Cepheid stars, as well as the subdwarf and white dwarf stars. Beyond the classical instability strip lie also the slowly pulsating B stars and the beta Cephei variables. -
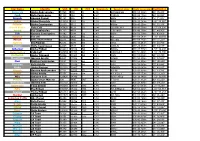
Star Name Identity SAO HD FK5 Magnitude Spectral Class Right Ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B
Star Name Identity SAO HD FK5 Magnitude Spectral class Right ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B8IVpMnHg 00h 08,388m 29° 05,433' Caph Beta Cassiopeiae 21133 432 2 2,27 F2III-IV 00h 09,178m 59° 08,983' Algenib Gamma Pegasi 91781 886 7 2,83 B2IV 00h 13,237m 15° 11,017' Ankaa Alpha Phoenicis 215093 2261 12 2,39 K0III 00h 26,283m - 42° 18,367' Schedar Alpha Cassiopeiae 21609 3712 21 2,23 K0IIIa 00h 40,508m 56° 32,233' Deneb Kaitos Beta Ceti 147420 4128 22 2,04 G9.5IIICH-1 00h 43,590m - 17° 59,200' Achird Eta Cassiopeiae 21732 4614 3,44 F9V+dM0 00h 49,100m 57° 48,950' Tsih Gamma Cassiopeiae 11482 5394 32 2,47 B0IVe 00h 56,708m 60° 43,000' Haratan Eta ceti 147632 6805 40 3,45 K1 01h 08,583m - 10° 10,933' Mirach Beta Andromedae 54471 6860 42 2,06 M0+IIIa 01h 09,732m 35° 37,233' Alpherg Eta Piscium 92484 9270 50 3,62 G8III 01h 13,483m 15° 20,750' Rukbah Delta Cassiopeiae 22268 8538 48 2,66 A5III-IV 01h 25,817m 60° 14,117' Achernar Alpha Eridani 232481 10144 54 0,46 B3Vpe 01h 37,715m - 57° 14,200' Baten Kaitos Zeta Ceti 148059 11353 62 3,74 K0IIIBa0.1 01h 51,460m - 10° 20,100' Mothallah Alpha Trianguli 74996 11443 64 3,41 F6IV 01h 53,082m 29° 34,733' Mesarthim Gamma Arietis 92681 11502 3,88 A1pSi 01h 53,530m 19° 17,617' Navi Epsilon Cassiopeiae 12031 11415 63 3,38 B3III 01h 54,395m 63° 40,200' Sheratan Beta Arietis 75012 11636 66 2,64 A5V 01h 54,640m 20° 48,483' Risha Alpha Piscium 110291 12447 3,79 A0pSiSr 02h 02,047m 02° 45,817' Almach Gamma Andromedae 37734 12533 73 2,26 K3-IIb 02h 03,900m 42° 19,783' Hamal Alpha