DOCSLIB.ORG

Stiffness Matrix for a Bar Element

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Stiffness Matrix for a Bar Element CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 1/44 Chapter 3b – Development of Truss Equations Learning Objectives • To derive the stiffness matrix for a bar element. • To illustrate how to solve a bar assemblage by the direct stiffness method. • To introduce guidelines for selecting displacement functions. • To describe the concept of transformation of vectors in two different coordinate systems in the plane. • To derive the stiffness matrix for a bar arbitrarily oriented in the plane. • To demonstrate how to compute stress for a bar in the plane. • To show how to solve a plane truss problem. • To develop the transformation matrix in three- dimensional space and show how to use it to derive the stiffness matrix for a bar arbitrarily oriented in space. • To demonstrate the solution of space trusses. Stiffness Matrix for a Bar Element Inclined, or Skewed Supports If a support is inclined, or skewed, at some angle for the global x axis, as shown below, the boundary conditions on the displacements are not in the global x-y directions but in the x’-y’ directions. CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 2/44 Stiffness Matrix for a Bar Element Inclined, or Skewed, Supports We must transform the local boundary condition of v’3 = 0 (in local coordinates) into the global x-y system. Stiffness Matrix for a Bar Element Inclined, or Skewed, Supports Therefore, the relationship between of the components of the displacement in the local and the global coordinate systems at node 3 is: uu'33cos sin vv'33sin cos We can rewrite the above expression as: cos sin t dtd'[]333 3 sin cos We can apply this sort of transformation to the entire displacement vector as: T dTdordTd'[] 11 []' CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 3/44 Stiffness Matrix for a Bar Element Inclined, or Skewed, Supports T Where the matrix [T1] is: []I [0] [0] []TIT [0][][0] 1 [0] [0] [t3 ] Both the identity matrix [I] and the matrix [t3] are 2 x 2 matrices. The force vector can be transformed by using the same transformation. fTf'[] 1 In global coordinates, the force-displacement equations are: fKd [] Stiffness Matrix for a Bar Element Inclined, or Skewed, Supports Applying the skewed support transformation to both sides of the equation gives: fKd [] []Tf11 [][] TKd By using the relationship between the local and the global displacements, the force-displacement equations become: T T dTd []1 ' fTKTd'[][][]' 11 Therefore the global equations become: F1x u1 F v 1y 1 F2x T u2 [][][]TKT11 F 2y v2 F '3x u ' 3 F ' 3y v '3 CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 4/44 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem Consider the plane truss shown below. Assume E = 210 GPa, A = 6 x 10-4 m2 for element 1 and 2, and A = 2 (6 x 10-4)m2 for element 3. Determine the stiffness matrix for each element. CC22CS CS 22 AE CSSS CS k LCSCSCC22 22 CSSS CS Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem The global elemental stiffness matrix for element 1 is: CC22CS CS 22 AE CSSS CS k LCSCSCC22 22 CSSS CS cos (1) 0 sin (1) 1 uvuv1122 0000 62 42 (210 10kN / m )(6 10 m ) 0101 k(1) 1 m 0000 0101 CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 5/44 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem The global elemental stiffness matrix for element 2 is: CC22CS CS 22 AE CSSS CS k LCSCSCC22 22 CSSS CS cos (2) 1 sin (2) 0 uv22 u 3 v 3 10 10 62 42 (210 10kN / m )(6 10 m ) 00 00 k(2) 1 m 10 10 00 00 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem The global elemental stiffness matrix for element 3 is: CC22CS CS 22 AE CSSS CS k LCSCSCC22 22 CSSS CS 2 2 cos (3) sin (3) 2 2 uv11 uv 3 3 1 111 62 42 (210 10kN / m )(6 2 10m ) 1 111 k(3) 22m 1111 1111 CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 6/44 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem Using the direct stiffness method, the global stiffness matrix is: 5.0 5.0 0 0 5.0 5.0 5.0 5.1 0 1 5.0 5.0 0 0 1 0 1 0 K 10260,1 5 N m 0 1 0 1 0 0 5.0 5.0 1 0 5.1 5.0 5.0 5.0 0 0 5.0 5.0 We must transform the global displacements into local coordinates. Therefore the transformation [T1] is: 1000 0 0 0100 0 0 []I [0] [0] 00 10 0 0 []TI1 [0][][0] 000 1 0 0 [0] [0] [t ] 3 22 0000 22 22 0000 22 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem The first step in the matrix transformation to find the product of [T1][K]. T1 K 1000 0 0 0.5 0.5 0 0 0.5 0.5 0100 0 00.5 1.5 0 1 0.5 0.5 00 10 0 0 00 1010 TK1, 260 105 N 1 m 010100 000 1 0 0 220.707 0.707 0.707 0 1.414 0.707 0000 22 220 0 0.707 0 0.707 0 0000 22 0.5 0.5 0 0 0.5 0.5 0.5 1.5 0 1 0.5 0.5 5 N 00 1010 TK1 1,260 10 m 010100 0.707 0.707 0.707 0 1.414 0.707 0 0 0.707 0 0.707 0 CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 7/44 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem The next step in the matrix transformation to find the product of T [T1][K][T1] . T TK1 T1 10 0 0 0 0 0.5 0.5 0 0 0.5 0.5 0.5 1.5 0 1 0.5 0.5 0100 0 0 T 00 1010 00 10 0 0 TKT 1, 2 6 0 1 0 5 N 1 1 m 010100 000 1 0 0 0.707 0.707 0.707 0 1.414 0.707 22 0000 22 0 0 0.707 0 0.707 0 22 0000 22 0.5 0.5 0 0 0.707 0 0.5 1.5 0 1 0.707 0 T 5 N 0 0 1 0 0.707 0.707 TK1 T 1,260 10 1 m 010100 0.707 0.707 0.707 0 1.5 0.5 0 0 0.707 0 0.5 0.5 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem The displacement boundary conditions are: uvv112 v'0 3 u F1x 0.5 0.5 0 0 0.707 0 1 v F1y 0.5 1.5 0 1 0.707 0 1 F 0 0 1 0 0.707 0.707 u2 2x 1, 2 6 0 1 0 5 N F m v 2y 010100 2 F ' 0.707 0.707 0.707 0 1.5 0.5 u' 3x 3 F ' 0 0 0.707 0 0.5 0.5 3y v '3 CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 8/44 Stiffness Matrix for a Bar Element Example 9 – Space Truss Problem By applying the boundary conditions the global force- displacement equations are: 1 0.707 u FkN 1,000 1,260 105 N 2 2x m 0.707 1.5 u '3 F '03x Solving the equation gives: umm2 11.91 umm'5.613 Stiffness Matrix for a Bar Element F Example 9 – Space Truss Problem 1x u1 F v 1y 1 F2x T u2 [][][]TKT F 11 2y v2 The global nodal forces are calculated as: F ' u ' 3x 3 F ' 3y v '3 F1x F 0.5 0.5 0 0 0.707 0 0 1y 0.5 1.5 0 1 0.707 0 0 F 2x 2 N 0 0 1 0 0.707 0.707 11.91 1, 2 6 0 1 0 mm F 0101000 2y F ' 0.707 0.707 0.707 0 1.5 0.5 5.61 3x 0 0 0.707 0 0.5 0.5 0 F '3y Therefore: FkNFkN11xy500 500 FFk23yy0'707N CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 9/44 Stiffness Matrix for a Bar Element Potential Energy Approach to Derive Bar Element Equations Let’s derive the equations for a bar element using the principle of minimum potential energy. The total potential energy, p, is defined as the sum of the internal strain energy U and the potential energy of the external forces : p U The differential internal work (strain energy) dU in a one- dimensional bar element is: dU xx()()() y z x d Stiffness Matrix for a Bar Element Potential Energy Approach to Derive Bar Element Equations If we let the volume of the element approach zero, then: dU xx d dV Summing the differential energy over the whole bar gives: x x 1 2 UddV Ed dV EdV xx xx 2 x V 0 V 0 V For a linear-elastic material (Hooke’s law) as shown below: 1 E UdV xx xx V 2 CIVL 7/8117 Chapter 3 - Truss Equations - Part 2 10/44 Stiffness Matrix for a Bar Element Potential Energy Approach to Derive Bar Element Equations The internal strain energy statement becomes 1 UdV xx 2 V The potential energy of the external forces is: M XudV Tu dS fu bxs ixi VSi1 where Xb is the body force (force per unit volume), Tx is the traction (force per unit area), and fix is the nodal concentrated force.
Load more

Recommended publications
  • How Can We Create Environments Where Hate Cannot Flourish?
    How can we create environments where hate cannot flourish? Saturday, February 1 9:30 a.m. – 10:00 a.m. Check-In and Registration Location: Field Museum West Entrance 10:00 a.m. – 10:30 a.m. Introductions and Program Kick-Off JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 10:30 a.m. – 11:30 a.m. Watch “The Path to Nazi Genocide” and Reflections JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 11:30 a.m. – 11:45 a.m. Break and walk to State of Deception 11:45 a.m. – 12:30 p.m. Visit State of Deception Interpretation by Holocaust Survivor Volunteers from the Illinois Holocaust Museum Location: Upper level 12:30 p.m. – 1:00 p.m. Breakout Session: Reflections on Exhibit Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B Saturday, February 2 (continued) 1:00 p.m. – 1:45 p.m. Lunch 1:45 p.m. – 2:45 p.m. A Survivor’s Personal Story Bob Behr, USHMM Survivor Volunteer Interviewed by: Ann Weber, USHMM Program Coordinator Location: Lecture Hall 1 2:45 p.m. – 3:00 p.m. Break 3:00 p.m. – 3:45 p.m. Student Panel: Beyond Indifference Location: Lecture Hall 1 Moderator: Emma Pettit, Sustained Dialogue Campus Network Student/Alumni Panelists: Jazzy Johnson, Northwestern University Mary Giardina, The Ohio State University Nory Kaplan-Kelly, University of Chicago 3:45 p.m. – 4:30 p.m. Breakout Session: Sharing Personal Reflections Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B 4:30 p.m.
    [Show full text]
  • ENIGMA X Aka SPARKLE Enclosure Manual Ver 7 012017
    ENIGMA-X / SPARKLE* ENCLOSURE SHOWER ENCLOSURE INSTALLATION INSTRUCTIONS IMPORTANT DreamLine® reserves the right to alter, modify or redesign products at any time without prior notice. For the latest up-to-date technical drawings, manuals, warranty information or additional details please refer to your model’s web page on DreamLine.com MODEL #s MODEL #s SHEN-6134480-## SHEN-6134720-## SHEN-6134600-## ##=finish *The SPARKLE model name designates an option with MirrorMax patterned glass. 07- Brushed Stainless Steel The installation is identical to the Enigma-X. 08- Polished Stainless Steel Right Hand Return panel installation shown 18- Tuxedo For more information about DreamLine® Shower Doors & Tub Doors please visit DreamLine.com ENIGMA-X / SPARKLE Enclosure manual Ver 7 01/2017 This model is treated with DreamLine’s exclusive ClearMaxTM Glass technology. This is a specially formulated coating that prevents the build up of soap and water spots. Install the surface with the ClearMaxTM label towards the inside of the shower. Please note that depending on the model, the glass may be coated on either one or both surfaces. For best results, squeegee the glass after each use and dry with a soft cloth. ENIGMA-X / SPARKLE Enclosure manual Ver 7 01/2017 2 B B A A C ! E IMPORTANT INFORMATION REGARDING THE INSTALLATION OF THIS SHOWER DOOR D PANEL DOOR F Right hand door installation shown as an example A Guide Rail Brackets must be firmly D Roller Guards must be postioned and attached to the wall. Installation into a secured within 1/16” of Upper Guide Rail. stud is strongly recommended.
    [Show full text]
  • Form 1095-B Health Coverage Department of the Treasury ▶ Do Not Attach to Your Tax Return
    560118 VOID OMB No. 1545-2252 Form 1095-B Health Coverage Department of the Treasury ▶ Do not attach to your tax return. Keep for your records. CORRECTED 2020 Internal Revenue Service ▶ Go to www.irs.gov/Form1095B for instructions and the latest information. Part I Responsible Individual 1 Name of responsible individual–First name, middle name, last name 2 Social security number (SSN) or other TIN 3 Date of birth (if SSN or other TIN is not available) 4 Street address (including apartment no.) 5 City or town 6 State or province 7 Country and ZIP or foreign postal code 9 Reserved 8 Enter letter identifying Origin of the Health Coverage (see instructions for codes): . ▶ Part II Information About Certain Employer-Sponsored Coverage (see instructions) 10 Employer name 11 Employer identification number (EIN) 12 Street address (including room or suite no.) 13 City or town 14 State or province 15 Country and ZIP or foreign postal code Part III Issuer or Other Coverage Provider (see instructions) 16 Name 17 Employer identification number (EIN) 18 Contact telephone number 19 Street address (including room or suite no.) 20 City or town 21 State or province 22 Country and ZIP or foreign postal code Part IV Covered Individuals (Enter the information for each covered individual.) (a) Name of covered individual(s) (b) SSN or other TIN (c) DOB (if SSN or other (d) Covered (e) Months of coverage First name, middle initial, last name TIN is not available) all 12 months Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 23 24 25 26 27 28 For Privacy Act and Paperwork Reduction Act Notice, see separate instructions.
    [Show full text]
  • State of New Physics in B->S Transitions
    New physics in b ! s transitions after LHC run 1 Wolfgang Altmannshofera and David M. Straubb a Perimeter Institute for Theoretical Physics, 31 Caroline St. N, Waterloo, Ontario, Canada N2L 2Y5 b Excellence Cluster Universe, TUM, Boltzmannstr. 2, 85748 Garching, Germany E-mail: [email protected], [email protected] We present results of global fits of all relevant experimental data on rare b s decays. We observe significant tensions between the Standard Model predictions! and the data. After critically reviewing the possible sources of theoretical uncer- tainties, we find that within the Standard Model, the tensions could be explained if there are unaccounted hadronic effects much larger than our estimates. Assuming hadronic uncertainties are estimated in a sufficiently conservative way, we discuss the implications of the experimental results on new physics, both model indepen- dently as well as in the context of the minimal supersymmetric standard model and models with flavour-changing Z0 bosons. We discuss in detail the violation of lepton flavour universality as hinted by the current data and make predictions for additional lepton flavour universality tests that can be performed in the future. We find that the ratio of the forward-backward asymmetries in B K∗µ+µ− and B K∗e+e− at low dilepton invariant mass is a particularly sensitive! probe of lepton! flavour universality and allows to distinguish between different new physics scenarios that give the best description of the current data. Contents 1. Introduction2 2. Observables and uncertainties3 2.1. Effective Hamiltonian . .4 2.2. B Kµ+µ− .....................................4 2.3. B ! K∗µ+µ− and B K∗γ ............................6 ! + − ! 2.4.
    [Show full text]
  • Percent R, X and Z Based on Transformer KVA
    SHORT CIRCUIT FAULT CALCULATIONS Short circuit fault calculations as required to be performed on all electrical service entrances by National Electrical Code 110-9, 110-10. These calculations are made to assure that the service equipment will clear a fault in case of short circuit. To perform the fault calculations the following information must be obtained: 1. Available Power Company Short circuit KVA at transformer primary : Contact Power Company, may also be given in terms of R + jX. 2. Length of service drop from transformer to building, Type and size of conductor, ie., 250 MCM, aluminum. 3. Impedance of transformer, KVA size. A. %R = Percent Resistance B. %X = Percent Reactance C. %Z = Percent Impedance D. KVA = Kilovoltamp size of transformer. ( Obtain for each transformer if in Bank of 2 or 3) 4. If service entrance consists of several different sizes of conductors, each must be adjusted by (Ohms for 1 conductor) (Number of conductors) This must be done for R and X Three Phase Systems Wye Systems: 120/208V 3∅, 4 wire 277/480V 3∅ 4 wire Delta Systems: 120/240V 3∅, 4 wire 240V 3∅, 3 wire 480 V 3∅, 3 wire Single Phase Systems: Voltage 120/240V 1∅, 3 wire. Separate line to line and line to neutral calculations must be done for single phase systems. Voltage in equations (KV) is the secondary transformer voltage, line to line. Base KVA is 10,000 in all examples. Only those components actually in the system have to be included, each component must have an X and an R value. Neutral size is assumed to be the same size as the phase conductors.
    [Show full text]
  • A Quotient Rule Integration by Parts Formula Jennifer Switkes ([email protected]), California State Polytechnic Univer- Sity, Pomona, CA 91768
    A Quotient Rule Integration by Parts Formula Jennifer Switkes ([email protected]), California State Polytechnic Univer- sity, Pomona, CA 91768 In a recent calculus course, I introduced the technique of Integration by Parts as an integration rule corresponding to the Product Rule for differentiation. I showed my students the standard derivation of the Integration by Parts formula as presented in [1]: By the Product Rule, if f (x) and g(x) are differentiable functions, then d f (x)g(x) = f (x)g(x) + g(x) f (x). dx Integrating on both sides of this equation, f (x)g(x) + g(x) f (x) dx = f (x)g(x), which may be rearranged to obtain f (x)g(x) dx = f (x)g(x) − g(x) f (x) dx. Letting U = f (x) and V = g(x) and observing that dU = f (x) dx and dV = g(x) dx, we obtain the familiar Integration by Parts formula UdV= UV − VdU. (1) My student Victor asked if we could do a similar thing with the Quotient Rule. While the other students thought this was a crazy idea, I was intrigued. Below, I derive a Quotient Rule Integration by Parts formula, apply the resulting integration formula to an example, and discuss reasons why this formula does not appear in calculus texts. By the Quotient Rule, if f (x) and g(x) are differentiable functions, then ( ) ( ) ( ) − ( ) ( ) d f x = g x f x f x g x . dx g(x) [g(x)]2 Integrating both sides of this equation, we get f (x) g(x) f (x) − f (x)g(x) = dx.
    [Show full text]
  • CONSONANT DIGRAPH- /Ch/ at the Beginning of Words
    MINISTRY OF EDUCATION PRIMARY ENGAGEMENT PROGRAMME GRADE FOUR (4) WORKSHEET-TERM 3 SUBJECT: LITERACY WEEK 5: LESSON 1 Name: _______________________________ Date: __________________________ READING: CONSONANT DIGRAPH- /ch/ at the beginning of words FACTS/TIPS A consonant digraph is formed when two consonants work together to make one sound. Consonant digraph ch has three(3) different sounds. 1. /ch/ as in chair, chalk 2. /sh/ as in chef, 3. /k/ as in chaos Let us read these words. Listen to the beginning sound. 1. chalk 2. cheese 3. chip 4. champagne 2. chorus 5. Charmin 6. child 7. chew Read the text below Ms. Charmin and Mr. Philbert work at NAREI. Philbert is a driver and Charmin a clerk. One day our class teacher, Ms. Phillips took us on a field trip where we visited CARICOM, GUYSUCO AND NAREI. Our time spent at NAREI was awesome. We were shown the different departments. One brave pupil, Charlie, asked Ms. Charmin about the meaning of the word 78 NAREI. She told us that the word NAREI is an acronym that means National Agricultural Research and Extension Institute. Ms. Charmin then went on to explain to us the products that are made there. After our tour around the compound, she gave us huge packages of some of the products. We were so excited that we jumped for joy. We took a photograph with her, thanked her and then bid her farewell. On our way back to school we spoke of our day out. We all agreed that it was very informative. ON YOUR OWN Say the words below and listen to the beginning sound.
    [Show full text]
  • Grading System the Grades of A, B, C, D and P Are Passing Grades
    Grading System The grades of A, B, C, D and P are passing grades. Grades of F and U are failing grades. R and I are interim grades. Grades of W and X are final grades carrying no credit. Individual instructors determine criteria for letter grade assignments described in individual course syllabi. Explanation of Grades The quality of performance in any academic course is reported by a letter grade, assigned by the instructor. These grades denote the character of study and are assigned quality points as follows: A Excellent 4 grade points per credit B Good 3 grade points per credit C Average 2 grade points per credit D Poor 1 grade point per credit F Failure 0 grade points per credit I Incomplete No credit, used for verifiable, unavoidable reasons. Requirements for satisfactory completion are established through student/faculty consultation. Courses for which the grade of I (incomplete) is awarded must be completed by the end of the subsequent semester or another grade (A, B, C, D, F, W, P, R, S and U) is awarded by the instructor based upon completed course work. In the case of I grades earned at the end of the spring semester, students have through the end of the following fall semester to complete the requirements. In exceptional cases, extensions of time needed to complete course work for I grades may be granted beyond the subsequent semester, with the written approval of the vice president of learning. An I grade can change to a W grade only under documented mitigating circumstances. The vice president of learning must approve the grade change.
    [Show full text]
  • Band Radar Models FR-2115-B/2125-B/2155-B*/2135S-B
    R BlackBox type (with custom monitor) X/S – band Radar Models FR-2115-B/2125-B/2155-B*/2135S-B I 12, 25 and 50* kW T/R up X-band, 30 kW I Dual-radar/full function remote S-band inter-switching I SXGA PC monitor either CRT or color I New powerful processor with LCD high-speed, high-density gate array and I Optional ARP-26 Automatic Radar sophisticated software Plotting Aid (ARPA) on 40 targets I New cast aluminum scanner gearbox I Furuno's exclusive chart/radar overlay and new series of streamlined radiators technique by optional RP-26 VideoPlotter I Shared monitor utilization of Radar and I Easy to create radar maps PC systems with custom PC monitor switching system The BlackBox radar system FR-2115-B, FR-2125-B, FR-2155-B* and FR-2135S-B are custom configured by adding a user’s favorite display to the blackbox radar package. The package is based on a Furuno standard radar used in the FR-21x5-B series with (FURUNO) monitor which is designed to comply with IMO Res MSC.64(67) Annex 4 for shipborne radar and A.823 (19) for ARPA performance. The display unit may be selected from virtually any size of multi-sync PC monitor, either a CRT screen or flat panel LCD display. The blackbox radar system is suitable for various ships which require no specific type approval as a SOLAS compliant radar. The radar is available in a variety of configurations: 12, 25, 30 and 50* kW output, short or long antenna radiator, 24 or 42 rpm scanner, with standard Electronic Plotting Aid (EPA) and optional Automatic Radar Plotting Aid (ARPA).
    [Show full text]
  • ON the THEORY of KERNELS of SCHWARTZ1 (Lf)(X) = J S(X,Y)
    ON THE THEORY OF KERNELS OF SCHWARTZ1 LEON EHRENPREIS Let 3Ddenote the space of indefinitely differentiable functions of compact carrier on Euclidean space R of dimension p, and denote by 3D'the dual of 3D,that is, 30' is the space of distributions on R; we give 3Dand 3D' their usual topologies (see [2]). By 23D,23D' we denote re- spectively the spaces corresponding to 3Dand 3D'on AXA. Let L be any continuous linear map of 3D—»3D';then L. Schwartz has shown (see [3 ] for a summary of Schwartz' results, the details will appear in a series of articles in the Journal D'Analyse (Jerusalem)) that L can be represented by a kernel, i.e. there exists a distribution S on AXA so that we may write (symbolically) (Lf)(x) = j S(x,y)f(y)dy for any /G 3D. The purpose of this paper is to give a simple proof of this fact and to prove the following result: Let us give the space of continuous linear mappings of 3D—»3D'the compact-open topology (see [l]); then this topology is the same as that of the space 23D'. We shall also obtain an explicit expression for the topology of the space 2DXof continuous linear maps of 3D' into 3Dwith the compact- open topology. The elements of 3DXare those of jSD,but the topology of 23Dis stronger than that of 3DX.It is possible to extend the above methods and results to other spaces, e.g. the space S of Schwartz. Moreover, the methods and results can be easily extended to in- definitely differentiable manifolds and double coset spaces of Lie groups (cf.
    [Show full text]
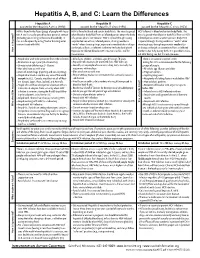
  • Hepatitis A, B, and C: Learn the Differences
    Hepatitis A, B, and C: Learn the Differences Hepatitis A Hepatitis B Hepatitis C caused by the hepatitis A virus (HAV) caused by the hepatitis B virus (HBV) caused by the hepatitis C virus (HCV) HAV is found in the feces (poop) of people with hepa- HBV is found in blood and certain body fluids. The virus is spread HCV is found in blood and certain body fluids. The titis A and is usually spread by close personal contact when blood or body fluid from an infected person enters the body virus is spread when blood or body fluid from an HCV- (including sex or living in the same household). It of a person who is not immune. HBV is spread through having infected person enters another person’s body. HCV can also be spread by eating food or drinking water unprotected sex with an infected person, sharing needles or is spread through sharing needles or “works” when contaminated with HAV. “works” when shooting drugs, exposure to needlesticks or sharps shooting drugs, through exposure to needlesticks on the job, or from an infected mother to her baby during birth. or sharps on the job, or sometimes from an infected How is it spread? Exposure to infected blood in ANY situation can be a risk for mother to her baby during birth. It is possible to trans- transmission. mit HCV during sex, but it is not common. • People who wish to be protected from HAV infection • All infants, children, and teens ages 0 through 18 years There is no vaccine to prevent HCV.
    [Show full text]
  • November 1960 Table of Contents
    AMERICAN MATHEMATICAL SOCIETY VOLUME 7, NUMBER 6 ISSUE NO. 49 NOVEMBER 1960 AMERICAN MATHEMATICAL SOCIETY Nottces Edited by GORDON L. WALKER Contents MEETINGS Calendar of Meetings ••••••••••.••••••••••••.••• 660 Program of the November Meeting in Nashville, Tennessee . 661 Abstracts for Meeting on Pages 721-732 Program of the November Meeting in Pasadena, California • 666 Abstracts for Meeting on Pages 733-746 Program of the November Meeting in Evanston, Illinois . • • 672 Abstracts for Meeting on Pages 747-760 PRELIMINARY ANNOUNCEMENT OF MEETINGS •.•.••••• 677 NEWS AND COMMENT FROM THE CONFERENCE BOARD OF THE MATHEMATICAL SCIENCES ••••••••••••.••• 680 FROM THE AMS SECRETARY •...•••.••••••••.•••.• 682 NEWS ITEMS AND ANNOUNCEMENTS .•••••.•••••••••• 683 FEATURE ARTICLES The Sino-American Conference on Intellectual Cooperation .• 689 National Academy of Sciences -National Research Council .• 693 International Congress of Applied Mechanics ..••••••••. 700 PERSONAL ITEMS ••.•.••.•••••••••••••••••••••• 702 LETTERS TO THE EDITOR.. • • • • • • • . • . • . 710 MEMORANDA TO MEMBERS The Employment Register . • . • • . • • • • • . • • • • 712 Employment of Retired Mathematicians ••••••.••••..• 712 Abstracts of Papers by Title • • . • . • • • . • . • • . • . • • . • 713 Reciprocity Agreement with the Societe Mathematique de Belgique .••.•••.••.••.•.•••••..•••••.•. 713 NEW PUBLICATIONS ..•..•••••••••.•••.•••••••••• 714 ABSTRACTS OF CONTRIBUTED PAPERS •.•••••••.••..• 715 RESERVATION FORM .•...•.•.•••••.••••..•••...• 767 MEETINGS CALENDAR OF MEETINGS Note: This Calendar lists all of the meetings which have been approved by the Council up to the date at which this issue of the NOTICES was sent to press. The summer and annual meetings are joint meetings of the Mathematical Asso­ ciation of America and the American Mathematical Society. The meeting dates which fall rather far in the future are subject to change. This is particularly true of the meetings to which no numbers have yet been assigned. Meet­ Deadline ing Date Place for No.
    [Show full text]