State of New Physics in B->S Transitions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

How Can We Create Environments Where Hate Cannot Flourish?
How can we create environments where hate cannot flourish? Saturday, February 1 9:30 a.m. – 10:00 a.m. Check-In and Registration Location: Field Museum West Entrance 10:00 a.m. – 10:30 a.m. Introductions and Program Kick-Off JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 10:30 a.m. – 11:30 a.m. Watch “The Path to Nazi Genocide” and Reflections JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 11:30 a.m. – 11:45 a.m. Break and walk to State of Deception 11:45 a.m. – 12:30 p.m. Visit State of Deception Interpretation by Holocaust Survivor Volunteers from the Illinois Holocaust Museum Location: Upper level 12:30 p.m. – 1:00 p.m. Breakout Session: Reflections on Exhibit Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B Saturday, February 2 (continued) 1:00 p.m. – 1:45 p.m. Lunch 1:45 p.m. – 2:45 p.m. A Survivor’s Personal Story Bob Behr, USHMM Survivor Volunteer Interviewed by: Ann Weber, USHMM Program Coordinator Location: Lecture Hall 1 2:45 p.m. – 3:00 p.m. Break 3:00 p.m. – 3:45 p.m. Student Panel: Beyond Indifference Location: Lecture Hall 1 Moderator: Emma Pettit, Sustained Dialogue Campus Network Student/Alumni Panelists: Jazzy Johnson, Northwestern University Mary Giardina, The Ohio State University Nory Kaplan-Kelly, University of Chicago 3:45 p.m. – 4:30 p.m. Breakout Session: Sharing Personal Reflections Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B 4:30 p.m. -

Form 1095-B Health Coverage Department of the Treasury ▶ Do Not Attach to Your Tax Return
560118 VOID OMB No. 1545-2252 Form 1095-B Health Coverage Department of the Treasury ▶ Do not attach to your tax return. Keep for your records. CORRECTED 2020 Internal Revenue Service ▶ Go to www.irs.gov/Form1095B for instructions and the latest information. Part I Responsible Individual 1 Name of responsible individual–First name, middle name, last name 2 Social security number (SSN) or other TIN 3 Date of birth (if SSN or other TIN is not available) 4 Street address (including apartment no.) 5 City or town 6 State or province 7 Country and ZIP or foreign postal code 9 Reserved 8 Enter letter identifying Origin of the Health Coverage (see instructions for codes): . ▶ Part II Information About Certain Employer-Sponsored Coverage (see instructions) 10 Employer name 11 Employer identification number (EIN) 12 Street address (including room or suite no.) 13 City or town 14 State or province 15 Country and ZIP or foreign postal code Part III Issuer or Other Coverage Provider (see instructions) 16 Name 17 Employer identification number (EIN) 18 Contact telephone number 19 Street address (including room or suite no.) 20 City or town 21 State or province 22 Country and ZIP or foreign postal code Part IV Covered Individuals (Enter the information for each covered individual.) (a) Name of covered individual(s) (b) SSN or other TIN (c) DOB (if SSN or other (d) Covered (e) Months of coverage First name, middle initial, last name TIN is not available) all 12 months Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 23 24 25 26 27 28 For Privacy Act and Paperwork Reduction Act Notice, see separate instructions. -

Grading System the Grades of A, B, C, D and P Are Passing Grades
Grading System The grades of A, B, C, D and P are passing grades. Grades of F and U are failing grades. R and I are interim grades. Grades of W and X are final grades carrying no credit. Individual instructors determine criteria for letter grade assignments described in individual course syllabi. Explanation of Grades The quality of performance in any academic course is reported by a letter grade, assigned by the instructor. These grades denote the character of study and are assigned quality points as follows: A Excellent 4 grade points per credit B Good 3 grade points per credit C Average 2 grade points per credit D Poor 1 grade point per credit F Failure 0 grade points per credit I Incomplete No credit, used for verifiable, unavoidable reasons. Requirements for satisfactory completion are established through student/faculty consultation. Courses for which the grade of I (incomplete) is awarded must be completed by the end of the subsequent semester or another grade (A, B, C, D, F, W, P, R, S and U) is awarded by the instructor based upon completed course work. In the case of I grades earned at the end of the spring semester, students have through the end of the following fall semester to complete the requirements. In exceptional cases, extensions of time needed to complete course work for I grades may be granted beyond the subsequent semester, with the written approval of the vice president of learning. An I grade can change to a W grade only under documented mitigating circumstances. The vice president of learning must approve the grade change. -
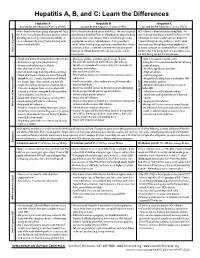
Hepatitis A, B, and C: Learn the Differences
Hepatitis A, B, and C: Learn the Differences Hepatitis A Hepatitis B Hepatitis C caused by the hepatitis A virus (HAV) caused by the hepatitis B virus (HBV) caused by the hepatitis C virus (HCV) HAV is found in the feces (poop) of people with hepa- HBV is found in blood and certain body fluids. The virus is spread HCV is found in blood and certain body fluids. The titis A and is usually spread by close personal contact when blood or body fluid from an infected person enters the body virus is spread when blood or body fluid from an HCV- (including sex or living in the same household). It of a person who is not immune. HBV is spread through having infected person enters another person’s body. HCV can also be spread by eating food or drinking water unprotected sex with an infected person, sharing needles or is spread through sharing needles or “works” when contaminated with HAV. “works” when shooting drugs, exposure to needlesticks or sharps shooting drugs, through exposure to needlesticks on the job, or from an infected mother to her baby during birth. or sharps on the job, or sometimes from an infected How is it spread? Exposure to infected blood in ANY situation can be a risk for mother to her baby during birth. It is possible to trans- transmission. mit HCV during sex, but it is not common. • People who wish to be protected from HAV infection • All infants, children, and teens ages 0 through 18 years There is no vaccine to prevent HCV. -

I/B/E/S DETAIL HISTORY a Guide to the Analyst-By-Analyst Historical Earnings Estimate Database
I/B/E/S DETAIL HISTORY A guide to the analyst-by-analyst historical earnings estimate database U.S. Edition CONTENTS page Overview..................................................................................................................................................................................................................1 File Explanations ..............................................................................................................................................................................................2 Detail File ..................................................................................................................................................................................................2 Identifier File..........................................................................................................................................................................................3 Adjustments File..................................................................................................................................................................................3 Excluded Estimates File ...............................................................................................................................................................3 Broker Translations...........................................................................................................................................................................4 S/I/G Codes..............................................................................................................................................................................................4 -

Alphabets, Letters and Diacritics in European Languages (As They Appear in Geography)
1 Vigleik Leira (Norway): [email protected] Alphabets, Letters and Diacritics in European Languages (as they appear in Geography) To the best of my knowledge English seems to be the only language which makes use of a "clean" Latin alphabet, i.d. there is no use of diacritics or special letters of any kind. All the other languages based on Latin letters employ, to a larger or lesser degree, some diacritics and/or some special letters. The survey below is purely literal. It has nothing to say on the pronunciation of the different letters. Information on the phonetic/phonemic values of the graphic entities must be sought elsewhere, in language specific descriptions. The 26 letters a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z may be considered the standard European alphabet. In this article the word diacritic is used with this meaning: any sign placed above, through or below a standard letter (among the 26 given above); disregarding the cases where the resulting letter (e.g. å in Norwegian) is considered an ordinary letter in the alphabet of the language where it is used. Albanian The alphabet (36 letters): a, b, c, ç, d, dh, e, ë, f, g, gj, h, i, j, k, l, ll, m, n, nj, o, p, q, r, rr, s, sh, t, th, u, v, x, xh, y, z, zh. Missing standard letter: w. Letters with diacritics: ç, ë. Sequences treated as one letter: dh, gj, ll, rr, sh, th, xh, zh. -
![Building the B[R]And: Understanding How Social Media Drives Consumer Engagement and Sales](https://docslib.b-cdn.net/cover/1301/building-the-b-r-and-understanding-how-social-media-drives-consumer-engagement-and-sales-801301.webp)
Building the B[R]And: Understanding How Social Media Drives Consumer Engagement and Sales
Marketing Science Institute Working Paper Series 2013 Report No. 13-113 Building the B[r]and: Understanding How Social Media Drives Consumer Engagement and Sales Yogesh V. Joshi , Liye Ma, William M. Rand, and Louiqa Raschid “Building the B[r]and: Understanding How Social Media Drives Consumer Engagement and Sales” © 2013 Yogesh V. Joshi , Liye Ma, William M. Rand, and Louiqa Raschid; Report Summary © 2013 Marketing Science Institute MSI working papers are distributed for the benefit of MSI corporate and academic members and the general public. Reports are not to be reproduced or published in any form or by any means, electronic or mechanical, without written permission. Report Summary Yogesh Joshi , Liye Ma, William Rand, and Louiqa Raschid investigate how activity in digital social media, by new and established brands, relates to engagement with consumers, and eventually, sales. Their dataset includes two years of Twitter activity and offline concerts for several musical bands, and the corresponding social media activity of the bands’ followers. In addition to measuring volume (that is, number of tweets sent per unit of time), the authors use machine learning methods to analyze message sentiment and informational content. They also collect A.C. Nielsen sales data for all albums released by these bands. They investigate the characteristics and evolution of consumers' engagement (propensity to tweet in response to a band’s tweets as well as propensity to send informational or emotional tweets) using a hidden Markov model. They relate engagement to sales via a generalized diffusion model. Findings Overall, the authors find that band actions in social media generate interest and change in engagement levels of their followers, and these engagement levels have a positive association with sales. -

Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone
Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Table of Contents 1. General Information 2 1.1 Use of Latin Script characters in domain names 3 1.2 Target Script for the Proposed Generation Panel 4 1.2.1 Diacritics 5 1.3 Countries with significant user communities using Latin script 6 2. Proposed Initial Composition of the Panel and Relationship with Past Work or Working Groups 7 3. Work Plan 13 3.1 Suggested Timeline with Significant Milestones 13 3.2 Sources for funding travel and logistics 16 3.3 Need for ICANN provided advisors 17 4. References 17 1 Generation Panel for Latin Script Label Generation Ruleset for the Root Zone 1. General Information The Latin script1 or Roman script is a major writing system of the world today, and the most widely used in terms of number of languages and number of speakers, with circa 70% of the world’s readers and writers making use of this script2 (Wikipedia). Historically, it is derived from the Greek alphabet, as is the Cyrillic script. The Greek alphabet is in turn derived from the Phoenician alphabet which dates to the mid-11th century BC and is itself based on older scripts. This explains why Latin, Cyrillic and Greek share some letters, which may become relevant to the ruleset in the form of cross-script variants. The Latin alphabet itself originated in Italy in the 7th Century BC. The original alphabet contained 21 upper case only letters: A, B, C, D, E, F, Z, H, I, K, L, M, N, O, P, Q, R, S, T, V and X. -

Early On: Differences in Part C & Part B Services
Booklet #2 Differences in Part C (Birth to 3) & Part B (3 to 5 Years) Services Early On… Guiding parents of infants and toddlers with special needs through the steps of early intervention supports and services in Wyoming Parent Information Center 500 W. Lott St, Suite A, Buffalo, WY 82834 (307) 684-2277 www.wpic.org -- 1 - Funding for this publication was provided, in part, by the Wyoming Department of Health, Early Intervention and Education Program. “Early On...” is a publication of the Parent Information Center, a project of Parents Helping Parents of WY, Inc., funded by the US Department of Education, Office of Special Education and Rehabilitative Services. Views expressed in this publication are not necessarily those of the US Department of Education. - 2 - What are the Parts? The Individuals with Disabilities Education Act (IDEA) is the federal law that governs special education services…and there’s a lot to it! In fact, there are four different parts to IDEA: Part A, Part B, Part C, and Part D. Part A lays out the basic foundation and covers general provisions and Part D covers national activities to improve education of children with disabilities. Parts B and C govern the provision of services for children with disabilities. The differences between Parts B and C is what this booklet will address. Part C applies specifically to infants and toddlers, ages birth through age 2, while Part B is for children ages 3 to 21 years of age. If your family is receiving early intervention services through infant and toddler programs under Part C, planning for the transition to Part B will happen before your child’s 3rd birthday. -

1 Symbols (2286)
1 Symbols (2286) USV Symbol Macro(s) Description 0009 \textHT <control> 000A \textLF <control> 000D \textCR <control> 0022 ” \textquotedbl QUOTATION MARK 0023 # \texthash NUMBER SIGN \textnumbersign 0024 $ \textdollar DOLLAR SIGN 0025 % \textpercent PERCENT SIGN 0026 & \textampersand AMPERSAND 0027 ’ \textquotesingle APOSTROPHE 0028 ( \textparenleft LEFT PARENTHESIS 0029 ) \textparenright RIGHT PARENTHESIS 002A * \textasteriskcentered ASTERISK 002B + \textMVPlus PLUS SIGN 002C , \textMVComma COMMA 002D - \textMVMinus HYPHEN-MINUS 002E . \textMVPeriod FULL STOP 002F / \textMVDivision SOLIDUS 0030 0 \textMVZero DIGIT ZERO 0031 1 \textMVOne DIGIT ONE 0032 2 \textMVTwo DIGIT TWO 0033 3 \textMVThree DIGIT THREE 0034 4 \textMVFour DIGIT FOUR 0035 5 \textMVFive DIGIT FIVE 0036 6 \textMVSix DIGIT SIX 0037 7 \textMVSeven DIGIT SEVEN 0038 8 \textMVEight DIGIT EIGHT 0039 9 \textMVNine DIGIT NINE 003C < \textless LESS-THAN SIGN 003D = \textequals EQUALS SIGN 003E > \textgreater GREATER-THAN SIGN 0040 @ \textMVAt COMMERCIAL AT 005C \ \textbackslash REVERSE SOLIDUS 005E ^ \textasciicircum CIRCUMFLEX ACCENT 005F _ \textunderscore LOW LINE 0060 ‘ \textasciigrave GRAVE ACCENT 0067 g \textg LATIN SMALL LETTER G 007B { \textbraceleft LEFT CURLY BRACKET 007C | \textbar VERTICAL LINE 007D } \textbraceright RIGHT CURLY BRACKET 007E ~ \textasciitilde TILDE 00A0 \nobreakspace NO-BREAK SPACE 00A1 ¡ \textexclamdown INVERTED EXCLAMATION MARK 00A2 ¢ \textcent CENT SIGN 00A3 £ \textsterling POUND SIGN 00A4 ¤ \textcurrency CURRENCY SIGN 00A5 ¥ \textyen YEN SIGN 00A6 -

Richard B. O'keeffe, Jr
Richard B. O'Keeffe, Jr. Partner − � 202.719.7396 � [email protected] Rick has more than 24 years of experience handling all aspects of Practice Areas the federal procurement matters. He is an expert in all stages of − federal contract law and litigation, including terminations, disputes, Construction protests, procurement integrity, post-Government employment, and Government Contracts National Security suspensions and debarments. Representative Matters Credentials − − Education ● Handles matters before the Armed Services Board of Contract LL.M., The George Washington University Law School Appeals (ASBCA), the Civilian Board of Contract Appeals LL.M., The Judge Advocate General's Legal (CBCA), the Small Business Administration (SBA), the Office of Center and School Hearings and Appeals (OHA), the U.S. Government J.D., William & Mary Law School B.A., with honors, University of Virginia Accountability Office (GAO), and the agency Suspension and Debarment Officials, along with internal investigations related Bar and Court Memberships District of Columbia Bar to fraud/false claims matters. Virginia Bar (Associate) ● Experienced in controversial, high-visibility cases, including U.S. Court of Appeals for the Federal Circuit complex litigation and more than 300 adversarial proceedings. U.S. Court of Federal Claims Notable cases include: ● Protest of Fluor Federal Solutions, LLC, B-410486, January 11, 2018 (Lead Counsel in four successive GAO bid protests relating to the Navy’s cost realism evaluation leading to, ultimately, a reversal of the award decision in Fluor’s favor which survived GAO protest). ● Protest of CAE USA, Inc., B-414259.6, December 18, 2017 (Lead Counsel in four successive GAO bid protests relating to the Army’s cost realism evaluation leading to, ultimately, a reversal of the award decision in client’s favor which survived GAO protest). -

How to Flourish in Social Work Infographic Transcript
How to Flourish in Social Work Preserving personal longevity and happiness, relationships, and your career Common Ailments “A feeling of depletion leads to dysfunction…a [Social Work] practitioner becomes increasingly ‘inoperative’.” Burnout Compassion Fatigue Secondary Traumatic Stress Steps to Self-Care Self-care refers to selected actions that restore balance in our personal and professional lives. Not just an add-on activity, self-care is also a state of mind through development of self- awareness, self-regulation, and self-efficacy. Exercise Light exercise 3 days a week improves happiness by 10-20% and increases work productivity by 15% Meditate 50% reduction in overall psychiatric symptoms 70% decrease in anxiety 44% reduction in common medical symptoms Read A new trend in treatment of mental illness; boosts creativity and activates sensory areas of the brain Greenspace Having over 30% of green space in your surroundings is recommended for healthy cortisol levels Laugh Laughter strengthens the immune system, boosts energy and diminishes pain. Children laugh over 300 times per day. The typical adult chuckles 15 times per day. Time Off 30% of employees use their vacation time, which leads to better quality sleep, decreased stress and improved mood. Eat Well Omega-3 fatty acids improve learning and memory and fight mental disorders. Carbohydrates aid in the release of endorphins Sleep The CDC currently classifies insufficient sleep as a public health epidemic. Sleep restores cognitive functions. For a self-care starter kit, please visit www.socialwork.buffalo.edu/students/self-care Sources: Adams, R. E., Figly, C. R., & Boscarino, J. A. (2008). The compassion fatigue scale: Its use with social workers following urban disaster.