DOCSLIB.ORG

Lect. 2: Nervous System I - Resting Potential

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lect. 2: Nervous System I - Resting Potential Organismal Lec 2 01/20/00 Lect. 2: Nervous System I - Resting Potential ASST.: READ CH. 5 and Ch 6 pp.163-174 I. Nervous System provided rapid communication throughout body and interaction with environment A. For rapid homeostatic control B. For conscious behavior II. Behavior is dictated by Nervous system A. Everything that is an animal’s behavior is determined by neural activity B. Basic unit is Nerve Cell 1. Pattern of connections with other nerve cells provides 2. Information processing 3. Patterns of activity for Behavior 4. Modulation of those connections Æ Modified behavior C. To understand how nervous system does all this must understand electrical properties of cells and their connections III. First some definitions A. Current (I) 1. Flow of electrical charge 2. Can be electrons (neg. current) 3. Can be positive ions (pos. current) 4. Although physicists generally refer to negative current flow, physiologists prefer to talk about positive ions 5. In analogy to flow of water through a hose, this is the water. B. Resistance (Ohms) 1. Resistance of current 2. In analogy to water, this is diameter of hose; i.e. how much hose restricts flow of water C. Voltage (V) 1. Force which drives current through a resistor 2. Force drops off as current goes through the resistor (IR drop) 3. Sometimes referred to as POTENTIAL DIFFERENCE; i.e. the potential force to Page 1 Organismal Lec 2 01/20/00 move current 4. In water analogy, this is difference in pressure between two points, can be due to difference in elevation between two points or pressure due to a pump a) Difference is low in gentle stream 5. Difference is very high at water fall 6. In voltage source there is charge separation as in a battery D. Conductor: Structure that allows current to flow easily E. Resistor: Element that reduces current flow F. Insulator: Element that prevents current flow (infinite resistance) G. Capacitor 1. Element that stores charge for current flow 2. In water analogy this is a weak spot in the wall of a hose 3. When pressure is increased all of it is not translated to end of hose 4. Some goes to bulge out wall 5. This stores pressure which can be used when pump is turned off to maintain pressure for short time H. Ohms law 1. Relationship of Current, Resistance and Voltage 2. V = IR IV. Nerve cells use Electrical signals for information A. Electrical potential already present across cell membrane of all cells 1. signals very fast 2. with amplification stations, can go long distances 3. various wave shapes can transport all kinds of information B. Source of MEMBRANE POTENTIAL 1. KCl placed in solution will eventually diffuse to uniform concentration a) Diffusion (1) Molecules are in constant motion (2) this is thermal energy; i.e. heat (3) In a concentration gradient (a) motion in both directions (b) more molecules to move down conc. grad. than up (c) so there is flux in both directions (d) however Net Flux is down conc. grad. Page 2 Organismal Lec 2 01/20/00 (e) Ultimately molecules will be uniformly distributed in equilibrium K K Net Flux (4) Rate of Diffusion (a) Fick's Law describes factors that affect diffusion rate (1) C1 - C2 (2) (A) = Cross-Sect. Area (3) Distance (L) (4) Temperature (5) Particle Size (D) Describe factors involved in Fick's law (i) Magnitude of conc. grad. (ii) Cross-sectional area through which molecules diffuse (iii) Distance over which diffusion takes place (iv) Rate of thermal motion - HEAT (v) Size of molecules - smaller particles move more rapidly than larger ones (vi) Net Flux = D A (C - C )/L 1 2 Page 3 Organismal Lec 2 01/20/00 (a) D = Diffusion coefficient (rate of thermal motion of a solute at standard temperature (b) A = Area available for diffusion (c) (C - C ) = Concentration gradient 1 2 (d) L = Distance diffusing particles must travel (e) Later in systems these factors will become very important 2. Divide into two chambers with MEMBRANE Membrane a) Lipid Bilayer b) Phospolipids associate in thermodynamically efficient way (1) Polar region out toward H2O (2) Non-polar regions tucked inside membrane c) Membrane has some selective effects on passage of different substances d) Permeability coefficient describes ease with which substance passes membrane (1) Non-polar molecules pass easily Page 4 Organismal Lec 2 01/20/00 (2) Polar molecules and ions not permeable (3) Oddly H2O goes right through membrane (a) small polar molecule (b) high kinetic energy (c) shoots through like a bullet going between phospholipid molecules e) In order to get ions or proteins through use Channels Channel (1) Protein pores (2) Imbedded in membrane (3) Acts as water tunnel through membrane (4) May have Selectivity filter (a) determines which substances can pass (b) e.g. K+ but not Na+ f) Can change permeability - Gated Channel (1) Voltage gated (2) Ligand gated 3. Channels in our membrane allow K through but NOT Cl 4. Equal amounts of KCl on both sides → NO VOLTAGE 5. Increase KCl on one side by 10x Page 5 Organismal Lec 2 01/20/00 10 K 1 K 10 Cl 1 Cl a) K wants to flow down concentration gradient but Cl cannot move b) For K to move down concentration gradient it would violate LAW OF ELECTRONEURTRALITY c) Chambers MUST remain ELECTRICALLY NEUTRAL (1) Positive charges = Negative charges 6. But because membrane is very thin, it can separate small amount of charge (SLIGHT violation of neutrality) a) A FEW K ions flow down concentration gradient b) But they are held against membrane by remaining Cl ions in left chamber + = - + = - + = - - - + + + - - - + + - + + + + - + - + - - - + - - + + + + - + - - + - - + + - - - + - + 7. Charge separation creates a voltage as in a battery Page 6 Organismal Lec 2 01/20/00 K Voltage 8. This voltage acts against further movement of K down gradient 9. When VOLTAGE = FORCE of K CHEMICAL GRADIENT system is in ELECTROCHEMICAL EQUILIBRIUM a) Stability requires that Voltage remains across membrane b) This is MEMBRANE POTENTIAL 10. Actually such a small amount of K ions move across membrane that CONCENTRATIONS are VIRTUALLY UNCHANGED a) So DON't try to ADD and SUBTRACT pos. and neg. CHARGES on either side to Æ voltage b) It will ALWAYS = ZERO 11. NOTE that since membrane potential OPPOSES chemical gradient, increasing K in left chamber makes left chamber MORE NEGATIVE with respect to right chamber 12. Can calculate membrane voltage with NERNST EQUATION: RT X E =×ln 1 X Fz X 2 R = gas constant z = valance of ion T = Absolute temp. ln = natural log F = Faraday's constant Ex = pot. side II - side I coulombs/g-equivalent charge) o a) At 18 C for MONOVALANT positive ion b) Equation reduces to Ex = 0.058 V log [x]1/[x]2 c) For NEGATIVE ion z = -1, so must switch to [x]2/[x]1 13. Membrane voltage for an ion at equilibrium is referred to as its Equilibrium + potential (EK is Equilibrium Potential for K ) Page 7 Organismal Lec 2 01/20/00 14. EK in most cells is ~ -90 mV a) This is because K is concentrated on inside of cell 15. ENA in most cells is ~+60 mV a) This is because Na is concentrated on outside of cell 16. Change concentration Æ predictable change in membrane potential 17. At equilibrium pot. no driving force for that ion 18. If membrane potential is displaced from the equilibrium pot., a driving force exists for that ion a) driving force is: (Memb. Pot. - EX) THIS IS IMPORTANT!!!!!!!!!!! Membrane Pot. Equilibrium Pot. for Ion X V = Driving Force on ion X Voltage → Driving Potential on Ion X Potential energy of (Memb. Pot. - EX) 19. In reality: a) Not just one ion permeable and b) Ions are not either 100% permeable or 100% impermeable c) The more permeable an ion is, the more it can move down its concentration gradient and the more dominant it is in membrane pot. 20. In a neuron: a) main permeable ions are: (1) K+ (2) Na+ (3) Cl- b) Resting pot. defined by extension of Nernst equation (1) Goldman equation: ++− RT PK[]++ P [ Na ] PCl [ ] E =×lnK out Na out Cl in m F PK[]++−++ P [ Na ] PCl [ ] K in Na in Cl out (2) Conc. differences maintained by Na-K pump (a) metabolic pump Page 8 Organismal Lec 2 01/20/00 (b) exchanges 3 Na+ for 2 K+ (c) Keeps ext. Na high and internal K high (d) Maintains Equilibrium potentials - (3) In most cells Cl moves passively so that ECl = Vm (4) Also permeability of Na+ ~ 0.01 x Perm of K+ (5) So Goldman equation reduces to: ++ RT PK[]+ 001. [ Na ] E =×ln K out out m F PK[]+++ 001. [ Na ] K in in + c) So RESTING POT. should approx. K equilibrium potential (EK) d) Hodgkin and Horowitz measured membrane pot. of frog muscle vs. Ext. K+ conc. 0 -20 Observed -40 -60 Calculated from Voltage -80 Nernst Equation -100 [K] o e) At lower end Vm deviates from EK because: (1) [K]o very low (2) [Na]o always high (3) So in this range 0.01 [Na]o starts to approach [K]o (4) So [Na] has some influence on membrane potential 21. Note that according to Goldman equation, membrane pot. Can be changed two ways a) Change CONCENTRATION of ions – this can be done experimentally but rarely occurs in animal because of homeostatic control of ion concentration b) Change in PERMEABILITY of ions – this is controlled by ion channels C. In most neurons at rest Vm ~ Ek ~ -60 to -90 mV Page 9 Organismal Lec 2 01/20/00 Penetrate Cell 0 mV -60 mV Ground + D.
Load more

Recommended publications
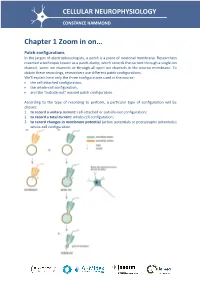
  • Chapter 1 Zoom in On… Patch Configurations in the Jargon of Electrophysiologists, a Patch Is a Piece of Neuronal Membrane
    CELLULAR NEUROPHYSIOLOGY CONSTANCE HAMMOND Chapter 1 Zoom in on… Patch configurations In the jargon of electrophysiologists, a patch is a piece of neuronal membrane. Researchers invented a technique known as a patch-clamp, which records the current through a single ion channel, some ion channels or through all open ion channels in the neuron membrane. To obtain these recordings, researchers use different patch configurations. We'll explain here only the three configurations used in the course: the cell-attached configuration, the whole-cell configuration, and the "outside-out" excised patch configuration. According to the type of recording to perform, a particular type of configuration will be chosen: 1. to record a unitary current: cell-attached or outside-out configuration; 2. to record a total current: whole-cell configuration; 3. to record changes in membrane potential (action potentials or postsynaptic potentials): whole-cell configuration. The cell-attached configuration (attached to the pipette - Figure a) First, the pipette is filled with an extracellular fluid. Positive pressure is applied in the electrode by means of a syringe connected to the electrode, so that the intrapipette fluid tends to leave the pipette. The electrode is then brought near to the soma of a neuron. When the electrode touches the membrane, the positive pressure is withdrawn to draw the membrane toward the mouth of the pipette. We wait without moving the pipette; a seal is made between the walls of the pipette and the soma membrane. This seal strength can be measured by applying a low level of amplitude current in the pipette. Since V = RI, one can measure the resistance of the seal.
    [Show full text]
  • A Thermodynamic Description for Physiological Transmembrane Transport
    A thermodynamic description for physiological transmembrane transport Marco Arieli Herrera-Valdez 1 1 Facultad de Ciencias, Universidad Nacional Autónoma de México marcoh@ciencias:unam:mx April 16, 2018 Abstract Physiological mechanisms for passive and active transmembrane transport have been theoretically described using many different approaches. A generic formulation for both passive and active transmem- brane transport, is derived from basic thermodynamical principles taking into account macroscopic forward and backward molecular fluxes, relative to a source compartment, respectively. Electrogenic fluxes also depend on the transmembrane potential and can be readily converted into currents. Interestingly, the conductance-based formulation for current is the linear approximation of the generic formulation for current, around the reversal potential. Also, other known formulas for current based on electrodiffusion turn out to be particular examples of the generic formulation. The applicability of the generic formulations is illustrated with models of transmembrane potential dynamics for cardiocytes and neurons. The generic formulations presented here provide a common ground for the biophysical study of physiological phenomena that depend on transmembrane transport. 1 Introduction One of the most important physiological mechanisms underlying communication within and between cells is the transport of molecules across membranes. Molecules can cross membranes either passively (Stein and Litman, 2014), or via active transport (Bennett, 1956). Passive transmembrane transport occurs through pores that may be spontaneously formed within the lipid bilayer (Blicher and Heimburg, 2013), or within transmembrane proteins called channels (Hille, 1992; Stein and Litman, 2014) that may be selective for particular ion types (Almers and McCleskey, 1984; Doyle et al., 1998; Favre et al., 1996).
    [Show full text]
  • Nernst Potentials and Membrane Potential Changes
    UNDERSTANDING MEMBRANE POTENTIAL CHANGES IN TERMS OF NERNST POTENTIALS: For seeing how a change in conductance to ions affects the membrane potential, follow these steps: 1. Make a graph with membrane potential on the vertical axis (-100 to +55) and time on the horizontal axis. 2. Draw dashed lines indicating the standard Nernst potential (equilibrium potential) for each ion: Na+ = +55 mV, K+ = -90mV, Cl- = -65 mV. 3. Draw lines below the horizontal axis showing the increased conductance to individual ions. 4. Start plotting the membrane potential on the left. Most graphs will start at resting potential (-70 mV) 5. When current injection (Stim) is present, move the membrane potential upward to Firing threshold. 6. For the time during which membrane conductance to a particular ion increases, move the membrane potential toward the Nernst potential for that ion. 7. During the time when conductance to a particular ion decreases, move the membrane potential away from the Nernst potential of that ion, toward a position which averages the conductances of the other ions. 8. When conductances return to their original value, membrane potential will go to its starting value. +55mV ACTION POTENTIAL SYNAPTIC POTENTIALS 0mV Membrane potential Firing threshold Firing threshold -65mV -90mV Time Time Na+ K+ Conductances Stim CHANGES IN MEMBRANE POTENTIAL ALLOW NEURONS TO COMMUNICATE The membrane potential of a neuron can be measured with an intracellular electrode. This 1 provides a measurement of the voltage difference between the inside of the cell and the outside. When there is no external input, the membrane potential will usually remain at a value called the resting potential.
    [Show full text]
  • Effect of Hyperkalemia on Membrane Potential: Depolarization
    ❖ CASE 3 A 6-year-old boy is brought to the family physician after his parents noticed that he had difficulty moving his arms and legs after a soccer game. About 10 minutes after leaving the field, the boy became so weak that he could not stand for about 30 minutes. Questioning revealed that he had complained of weakness after eating bananas, had frequent muscle spasms, and occasionally had myotonia, which was expressed as difficulty in releasing his grip or diffi- culty opening his eyes after squinting into the sun. After a thorough physical examination, the boy was diagnosed with hyperkalemic periodic paralysis. The family was advised to feed the boy carbohydrate-rich, low-potassium foods, give him glucose-containing drinks during attacks, and have him avoid strenuous exercise and fasting. ◆ What is the effect of hyperkalemia on cell membrane potential? ◆ What is responsible for the repolarizing phase of an action potential? ◆ What is the effect of prolonged depolarization on the skeletal muscle Na+ channel? 32 CASE FILES: PHYSIOLOGY ANSWERS TO CASE 3: ACTION POTENTIAL Summary: A 6-year-old boy who experiences profound weakness after exer- cise is diagnosed with hyperkalemic periodic paralysis. ◆ Effect of hyperkalemia on membrane potential: Depolarization. ◆ Repolarization mechanisms: Activation of voltage-gated K+ conductance and inactivation of Na+ conductance. ◆ Effect of prolonged depolarization: Inactivation of Na+ channels. CLINICAL CORRELATION Hyperkalemic periodic paralysis (HyperPP) is a dominant inherited trait caused by a mutation in the α subunit of the skeletal muscle Na+ channel. It occurs in approximately 1 in 100,000 people and is more common and more severe in males.
    [Show full text]
  • Electrical Activity of the Heart: Action Potential, Automaticity, and Conduction 1 & 2 Clive M
    Electrical Activity of the Heart: Action Potential, Automaticity, and Conduction 1 & 2 Clive M. Baumgarten, Ph.D. OBJECTIVES: 1. Describe the basic characteristics of cardiac electrical activity and the spread of the action potential through the heart 2. Compare the characteristics of action potentials in different parts of the heart 3. Describe how serum K modulates resting potential 4. Describe the ionic basis for the cardiac action potential and changes in ion currents during each phase of the action potential 5. Identify differences in electrical activity across the tissues of the heart 6. Describe the basis for normal automaticity 7. Describe the basis for excitability 8. Describe the basis for conduction of the cardiac action potential 9. Describe how the responsiveness relationship and the Na+ channel cycle modulate cardiac electrical activity I. BASIC ELECTROPHYSIOLOGIC CHARACTERISTICS OF CARDIAC MUSCLE A. Electrical activity is myogenic, i.e., it originates in the heart. The heart is an electrical syncitium (i.e., behaves as if one cell). The action potential spreads from cell-to-cell initiating contraction. Cardiac electrical activity is modulated by the autonomic nervous system. B. Cardiac cells are electrically coupled by low resistance conducting pathways gap junctions located at the intercalated disc, at the ends of cells, and at nexus, points of side-to-side contact. The low resistance pathways (wide channels) are formed by connexins. Connexins permit the flow of current and the spread of the action potential from cell-to-cell. C. Action potentials are much longer in duration in cardiac muscle (up to 400 msec) than in nerve or skeletal muscle (~5 msec).
    [Show full text]
  • 9.01 Introduction to Neuroscience Fall 2007
    MIT OpenCourseWare http://ocw.mit.edu 9.01 Introduction to Neuroscience Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 9.01 Recitation (R02) RECITATION #2: Tuesday, September 18th Review of Lectures: 3, 4 Reading: Chapters 3, 4 or Neuroscience: Exploring the Brain (3rd edition) Outline of Recitation: I. Previous Recitation: a. Questions on practice exam questions from last recitation? II. Review of Material: a. Exploiting Axoplasmic Transport b. Types of Glia c. THE RESTING MEMBRANE POTENTIAL d. THE ACTION POTENTIAL III. Practice Exam Questions IV. Questions on Pset? Exploiting Axoplasmic Transport: Maps connections of the brain Rates of transport: - slow: - fast: Examples: Uses anterograde transport: - Uses retrograde transport: - - - Types of Glia: - Microglia: - Astrocytes: - Myelinating Glia: 1 THE RESTING MEMBRANE POTENTIAL: The Cast of Chemicals: The Movement of Ions: ­ Influences by two factors: (1) Diffusion: (2) Electricity: Ohm’s Law: I = gV Ionic Equilibrium Potentials (EION): + Example: ENs * diffusional and electrical forces are equal 2 Nernst Equation: EION = 2.303 RT/zF log [ion]0/[ion]i Calculates equilibrium potential for a SINGLE ion. Inside Outside EION (at 37°C) + [K ] + [Na ] 2+ [Ca ] ­ [Cl ] *Pumps maintain concentration gradients (ex. sodium­potassium pump; calcium pump) Resting Membrane Potential (VM at rest): Measured resting membrane potential: ­ 65 mV Goldman Equation: + + + + VM = 61.54 mV log (PK[K ]o + PNa[Na ]o)/ (PK[K ]I + PNa[Na ]i) + + Calculates membrane potential when permeable to both Na and K . Remember: at REST, gK >>> gNa therefore, VM is closer to EK THE ACTION POTENTIAL (Nerve Impulse): Phases of an Action Potential: Vm (mV) ENa 0 EK Time 3 Conductance of Ion Channels during AP: Remember: Changes in conductance, or permeability of the membrane to a specific ion, changes the membrane potential.
    [Show full text]
  • The Action Potential
    See discussions, stats, and author profiles for this publication at: http://www.researchgate.net/publication/6316219 The action potential ARTICLE in PRACTICAL NEUROLOGY · JULY 2007 Source: PubMed CITATIONS READS 16 64 2 AUTHORS, INCLUDING: Mark W Barnett The University of Edinburgh 21 PUBLICATIONS 661 CITATIONS SEE PROFILE Available from: Mark W Barnett Retrieved on: 24 October 2015 192 Practical Neurology HOW TO UNDERSTAND IT Pract Neurol 2007; 7: 192–197 The action potential Mark W Barnett, Philip M Larkman t is over 60 years since Hodgkin and called ion channels that form the permeation Huxley1 made the first direct recording of pathways across the neuronal membrane. the electrical changes across the neuro- Although the first electrophysiological nal membrane that mediate the action recordings from individual ion channels were I 2 potential. Using an electrode placed inside a not made until the mid 1970s, Hodgkin and squid giant axon they were able to measure a Huxley predicted many of the properties now transmembrane potential of around 260 mV known to be key components of their inside relative to outside, under resting function: ion selectivity, the electrical basis conditions (this is called the resting mem- of voltage-sensitivity and, importantly, a brane potential). The action potential is a mechanism for quickly closing down the transient (,1 millisecond) reversal in the permeability pathways to ensure that the polarity of this transmembrane potential action potential only moves along the axon in which then moves from its point
    [Show full text]
  • Nernst Equation - Wikipedia 1 of 10
    Nernst equation - Wikipedia 1 of 10 Nernst equation In electrochemistry, the Nernst equation is an equation that relates the reduction potential of an electrochemical reaction (half-cell or full cell reaction) to the standard electrode potential, temperature, and activities (often approximated by concentrations) of the chemical species undergoing reduction and oxidation. It was named after Walther Nernst, a German physical chemist who formulated the equation.[1][2] Contents Expression Nernst potential Derivation Using Boltzmann factor Using thermodynamics (chemical potential) Relation to equilibrium Limitations Time dependence of the potential Significance to related scientific domains See also References External links Expression A quantitative relationship between cell potential and concentration of the ions Ox + z e− → Red standard thermodynamics says that the actual free energy change ΔG is related to the free o energy change under standard state ΔG by the relationship: where Qr is the reaction quotient. The cell potential E associated with the electrochemical reaction is defined as the decrease in Gibbs free energy per coulomb of charge transferred, which leads to the relationship . The constant F (the Faraday constant) is a unit conversion factor F = NAq, where NA is Avogadro's number and q is the fundamental https://en.wikipedia.org/wiki/Nernst_equation Nernst equation - Wikipedia 2 of 10 electron charge. This immediately leads to the Nernst equation, which for an electrochemical half-cell is . For a complete electrochemical reaction
    [Show full text]
  • Membrane Potentials As Signals
    Membrane Potentials as Signals The membrane potential allows a cell to function as a battery, providing electrical power to activities within the cell and between cells. KEY POINTS A membrane potential is the difference in electrical potential between the interior and the exterior of a biological cell. In electrically excitable cells, changes in membrane potential are used for transmitting signals within the cell. The opening and closing of ion channels can induce changes from the resting potential. Depolarization is when the interior voltage becomes more positive and hyperpolarization when it becomes more negative. TERMS Graded potentials Graded potentials vary in size and arise from the summation of the individual actions of ligand- gated ion channel proteins, and decrease over time and space. Depolarization Depolarization is a change in a cell's membrane potential, making it more positive, or less negative, and may result in generation of an action potential. Action potential A short term change in the electrical potential that travels along a cell such as a nerve or muscle fiber. EXAMPLE In neurons, a sufficiently large depolarization can evoke an action potential in which the membrane potential changes rapidly. Give us feedback on this content: Membrane potential (also transmembrane potential or membrane voltage) is the difference in electrical potential between the interior and the exterior of a biological cell. All animal cells are surrounded by a plasma membrane composed of a lipid bilayer with a variety of types of proteins embedded in it. The membrane serves as both an insulator and a diffusion barrier to the movement of ions.
    [Show full text]
  • 1 Probing the Membrane Potential of Living Cells by Dielectric
    Probing the membrane potential of living cells by dielectric spectroscopy Corina Bot and Camelia Prodan Dept. of Physics, New Jersey Inst. of Techn, Newark, NJ Abstract. In this paper we demonstrate a quantitative way to measure the membrane potential of live cells by dielectric spectroscopy. We also show that the values of the membrane potential obtained using our technique are in good agreement with those obtained using traditional methods-voltage sensitive dyes. The membrane potential is determined by fitting the experimental dielectric dispersion curves with the dispersion curves obtain from a theoretical model. Variations in the membrane potential were induced by modifying the concentration of potassium chloride in the solution of the cell suspension in the presence of valinomycin. For exemplification of the method, E. coli were chosen for our experiments. Introduction The resting membrane potential is one of the most important living cell parameters. By monitoring a cell’s membrane potential, one can get important information about its state. Changes in the membrane potential have been linked to different diseases, including Parkinson’s, epilepsy and Bartter’s syndrome [1]. A decrease in the plasma membrane potential has been seen in tumor cells with increased expression of multi-drug resistance (MDR) protein, also known as P-glycoprotein [2]. It was also shown that the membrane potential plays a critical role in the antibiotic uptake by cells and in bactericidal action [3]. Thus measuring or monitoring the membrane potential is of great importance. The existing “gold” or standard methods to measure or monitor the membrane potential are patch clamping and voltage sensitive dyes.
    [Show full text]
  • Chapter 7 Transport of Ions in Solution and Across Membranes
    Chapter 7 Transport of ions in solution and across membranes 7-1. Introduction 7-2. Ionic fluxes in solutions 7-2.1. Fluxes due to an electrical field in a solution 7-2.2. Flux due to an electrochemical potential gradient 7-3. Transmembrane potentials 7-3.1. The Nernst potential, the single ion case where the flux is zero 7-3.2. Current-voltage relationships of ionic channels 7-3.3. The constant field approximation 7-3.4. The case of a neutral particle 7-4. The resting transmembrane potential, ER 7-4.1. Goldman-Hodgkin-Katz expression for the resting potential 7-4.2. Gibbs-Donnan equilibrium and the Donnan potential 7-4.3. Electrodiffusion 7-5. Patch clamp studies of single-channel kinetics 7-6. The action potential in excitable cells 7-6.1. Neuronal currents 7-6.2. The Hodgkin-Huxley nerve action potential 7-6.3. The voltage clamp methods for measuring transmembrane currents 7-6.4. Functional behavior of the nerve axon action potential 7-6.5. Cardiac and other action potentials 7-7. Propagation of the action potential 7-7.1. The cable equations 7-7.2. The velocity of propagation 7-8. Maintaining ionic balance: Pumps and exchangers 7-9. Volume changes with ionic fluxes 7-10. Summary 7-11. Further reading 7-12. Problems 7-13. References 7-13.1. References from previous reference list not appearing in current text or references This chapter lacks the following: Tables and programs. Completion of later parts on the pumps. Complete cross referencing. Improvements in Figures.
    [Show full text]
  • Resting Potential and Chloride Channels
    Neurobiology – resting potential and chloride channels Rudolf Cardinal, 4 Feb 99 • Ionic concentrations are determined and maintained by the activity of ionic pumps, including the Na+–K+ ATPase (pumping 3 + + + – + – + + Na out and 2 K in), the K /Cl cotransporter (using the K gradient to extrude Cl ), the active Ca pump (extruding Ca and us- ing ATP) and the Na+/Ca2+ exchanger (using the Na+ gradient to extrude Ca+, 3 Na+ in to 1 Ca2+ out). Action potentials involve the transfer of too few ions to affect the ionic concentration significantly (a drop in the ocean) so we can ignore their effects. • Actual ionic concentrations in mammalian neurons: Ion Internal concentration External concentration Valence (z) Equilibrium potential Na+ 15 mM 150 mM +1 +62 mV K+ 150 mM 5.5 mM +1 –89 mV Cl– 9 mM 125 mM –1 –71 mV Ca2+ 10–4 mM 1 mM +2 +124 mV • Equilibrium potential for each ion is determined solely by the concentration gradient and valence, by the Nernst equation: E = –1 –1 (RT/zF) ln(concout/concin). R is the gas constant (8.314 J deg mol ); T is the absolute temperature (37°C = 310 K); z is the va- lence for the ion; F is Faraday’s constant (96500 C mol–1); E is in volts. • Remember that an ion will not flow across a membrane if the potential gradient equals that ion’s equilibrium potential (by defi- nition). • The resting potential is determined by the equilibrium potentials for every ion to which the membrane is permeable, weighted + + – + + by the permeability (p), via th Goldman equation: E = (RT/F) ln[ (pK[K ]out + pNa[Na ]out + pCl[Cl ]in) / (pK[K ]in + pNa[Na ]in + – pCl[Cl ]out)].
    [Show full text]