DOCSLIB.ORG

University of Zimbabwe Faculty of Science

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
University of Zimbabwe Faculty of Science University of Zimbabwe Faculty of Science Atmospheric aerosol particles and transport: a climatological perspective for Zimbabwe by Daniel NYANGANYURA The thesis is submitted in partial fulfilment of the requirements for the Doctor of Philosophy Degree 2006 To my wife Maybe and to our two boys Pedro and Danilo who always give me the will to go on, and to my parents who although they lived in a different epoch, have contributed to what I became. Abstract Atmospheric aerosol particles were collected in the coarse (2-10 µm diameter) and fine (< 2 µm diameter) size fractions at Rukomechi research station, (16.1 °S, 29.4 °E, 500 m a.s.l.), northern Zimbabwe from September 1994 to January 2000. The collected samples were analysed for particulate mass (PM), black carbon and 47 elements at the Gent Institute for Nuclear Sciences. The main sources of coarse and fine aerosols were found to be crustal matter, sea salt and biomass burning for both wet and dry seasons. However, additional sources for copper and biogenic aerosols were detected during the wet and dry seasons, respectively, while anthropogenic influences were only found in the fine aerosols. The Absolute Principal Component Analysis (APCA) attributed 29% of the total wet season coarse particulate mass to the mixed biogenic/biomass burning component, while the major contribution (32%) was attributed to biomass burning during the dry season. The biomass burning component also provided the major contribution to the total fine particulate mass, accounting for 44% and 79% in the wet and dry seasons, respectively. The climatology of air mass transport to northern Zimbabwe was examined through an analysis of 5-day kinematic back trajectories arriving daily at Rukomechi at ~ 850 hPa for the period of 1994 to 1999. Classification of trajectories into different flow regimes was done using a non-hierarchical cluster algorithm. The dominant transport features include the eastern corridor, the south-east corridor, southern and north north-westerly flows, as well as regionally re-circulated air. The eastern corridor is comprised of fast and slow air masses that contribute 35% of the total number of trajectories. The air masses in these corridors bring late dry season to wet season air masses driven by an anticyclone that wraps around the subcontinent and stretches into the Mozambique Channel. The south-east corridor is also composed of fast and slow winds that contribute late wet season to dry season air masses and account for 44% of the total number of trajectories. These winds are associated with the Atlantic Ocean anticyclone and the Indian Ocean tropical depression. The fast dry season southern flow contributes 8% of the total number of trajectories and is driven by a continental anticyclone over South Africa coupled to an Atlantic Ocean anticyclone. The north north-westerly flow contributes least to the total number of trajectories (6%) and is associated with Inter- Tropical Convergence Zone while the regionally re-circulated air, as a result of differential heating at the surface, is the slowest. Of the seven air flows, only four were found carrying air significantly loaded with aerosols to northern Zimbabwe. These are namely: the fast easterly that carries aerosols mainly from biomass burning related sources; the slow south easterly that is associated with aerosols from various sources; the southerly containing mineral dust, sea salt and anthropogenic aerosols; and the regional flows that contain aerosols of anthropogenic origin. The potential sources of biomass burning aerosols were found to be due to fire activities from northern Zimbabwe and central Mozambique. The other pathways carry anthropogenic aerosols, especially copper (from areas around the Copper-belt regions), sulphur (from South African industrial areas), and lead (from the major Southern African road network). i Acknowledgements I am grateful for the contributions of several institutions and individuals who made this PhD thesis possible. I am grateful to the University of Zimbabwe, Department of Physics, for giving me the opportunity to do my PhD study. I am gratefully indebted to the German Academic Exchange Service (DAAD) and the Max Planck Society (partially through the Max Planck International Research School of Atmospheric Chemistry and Physics) for the financial support provided during the course of this research and to the Belgian Federal Science Policy Office for the financial support for the aerosol chemical analysis. I regard myself very privileged to have the opportunity to carry out this research under the guidance of my supervisors Dr A. Makarau, Dr M. Mathuthu and Prof F. X. Meixner. I’m particularly indebted to Prof F. X. Meixner whose commitment to my work is unmatched, and I appreciate his guidance, wisdom, and attention to detail. Big thanks also go to the Max Planck Institute for Chemistry, Biogeochemistry department group members, my office colleague Dr Ivonne Trebs and particularly to Dr. Günter Helas, for their unwavering support and for providing me with an excellent research environment. I am also indebted to Prof Meinrat O. Andreae who supported my studies and also provided logistical support. My gratitude also goes to Prof. W. Maenhaut (Institute of Nuclear Sciences, University of Gent, Belgium) for his assistance with data analysis, his valuable advice and support. I am also grateful to Prof. H. Wernli (Institute of Atmospheric Sciences, University of Mainz, Germany) for his valuable help and advice, and the European Centre for Medium Range Weather Forecasting for providing data for plotting the surface pressure maps and Dr G. Kirkman whose assistance in developing the fire plot procedure was very valuable and Dr A Lupu for developing the potential source contribution function procedure that was used in this study. I also thank M.-T. Fernández-Jiménez, I. Rajta, S. Dubtsov, D.J.A. De Ridder and N. Raes from Ghent University for the chemical analyses of the samples. I am also grateful to P. Chimanga, M. Chiranda and J. Mlambo from the Tsetse Control Branch, Harare, Zimbabwe, for collecting the aerosol samples at the Rukomechi site. I also thank Dr. Steve Torr (Natural Resources Institute, Chatham/U.K.) for providing the 1992-1999 data set of the automated meteorological station at Rukomechi. Finally, I would like to express my heart-felt gratitude to my wife, Maybe and our three boys Pedro, Danilo and Daniel Junior (a family that made a difference) for tolerating years of my absence from the family. ii Table of contents Abstract ......................................................................................................................... i Acknowledgements............................................................................................................... ii List of tables ....................................................................................................................... vi List of figures ...................................................................................................................... vii Chapter 1 Introduction.................................................................................................. 1 1.1 Background .......................................................................................................................... 1 1.2 Motivation for the research................................................................................................. 2 1.3 Objectives of the research ................................................................................................... 3 1.4 Layout of the chapters......................................................................................................... 4 Chapter 2 Theory .......................................................................................................... 5 2.1 Aerosols................................................................................................................................. 5 2.2 Sources of aerosols ............................................................................................................... 7 2.2.1 Mineral dust aerosols .......................................................................................................................8 2.2.2 Biogenic aerosols .............................................................................................................................8 2.2.3 Anthropogenic aerosols....................................................................................................................9 2.2.4 Marine aerosols ................................................................................................................................9 2.2.5 Biomass burning.............................................................................................................................10 2.3 Effects of aerosols............................................................................................................... 11 2.3.1 Direct and indirect effect on climate..............................................................................................11 2.3.2 Aerosol effects on human health and environment .......................................................................13 2.4 Aerosol sampling................................................................................................................13 2.5 Physical and elemental analysis of aerosols..................................................................... 16 2.5.1
Load more

Recommended publications
  • An Assessment of Source Water Quality in Karoi, Mashonaland West Province, Zimbabwe
    An Assessment of Source Water Quality in Karoi, Mashonaland West Province, Zimbabwe Gondo Reniko1 and W. Chingombe2 1Okavango Research Institute, University of Botswana, Maun, Botswana; 2University of Mpumalanga, School of Biology and Environmental Science, Mbombela, Republic of South Africa. Abstract The aim of this study was to assess the quality of source water used for domestic purposes in the town of Karoi. The objectives were: to determine the quality of surface water in the study area; and to characterize point and non-point sources of pollution. The study examined physical and chemical surface water quality parameters that may indicate pollution and so help to identify surface water pollution. The results showed that most of the measured parameters in surface water examined in Karoi were within the acceptable range of WHO drinking water guidelines. When compared with the guidelines, electrical conductivity was slightly higher; turbidity and total suspended solids were significantly higher in the wet season than in the dry season due to water flow- ing, which carries particles with it; and the changing seasons resulted in slight changes in surface water temperature. The results suggest that some human activities, like agriculture and poor sewage disposal in Karoi, can reduce surface water quality in Karoi. 1 Introduction hyacinth; pennywort, parrot’s feather and Kariba weed (Moyo et al. 2004). Water sources for drinking and other domestic purposes must The aquatic environment is the ultimate sink of wastewater possess high degrees of purity, free from chemical contamination generated by humans’ industrial, commercial and domestic ac- and microorganisms (Chinhanga 2010). In Zimbabwe, govern- tivities.
    [Show full text]
  • M GOVERNMENT GAZETTE
    A m ZIMBABWEAN GOVERNMENT GAZETTE Published by Authority Vol. LXVIII, No. 9 16th FEBRUARY, 1990 Price 40c General Notice 96 of 1990. 0/101/89. Motor-omnibus. Passenger-capacity: 76. Route: Masvingo - Masvingise - Nerupiri - Chimedza - Muka- ROAD MOTOR TRANSPORTATION ACT ro Mission - Gutu Township - Magombedze - Dewende - [CHAPTER 262] Zinhata - Vunjere. Applications in Connexion with Road Service Permits The service to operate as follows— (a) depart Masvingo Monday to Thursday 12 p.m., arrive Vunjere 4.30 p.m.; IN terms of subsection (4) of section 7 of the Road Motor (b) depart Masvingo Friday 5 p.m., arrive Vunjere Transportation Act [Chapter 262], notice is hereby given that the applications detailed in the Schedule, for the issue or 9.30 p.m.; amendment of road service permits, have been received for (c) depart Masvingo Saturday 1 p.m., arrive Vunjere the consideration of the Controller of Road Motor Transporta­ 5.30 p.m.; tion. (d) depart Masvingo Sunday 3 p.m., arrive Vunjere Any person wishing to object to any such application must 7.30 p.m.; lodge with the Controller of Road Motor Transportation, (e) depart Vunjere Monday to Saturday 5 a.m., arrive Ma­ P.O. Box 8332, Causeway— svingo 9.30 a.m.; (a) a notice, in writing, of his intention to object, so as to (t) depart Vunjere Sunday 8 a.m., arrive Masvingo reach the Controller’s ofHce not later than the 9th 12.30 p.m. March, 1990; Note.—This application is made to reinstate permit 25353 (b) his objection and the grounds therefor, on form R.M.T.
    [Show full text]
  • Health Cluster Bulletin 11Ver2
    Zimbabwe Health Cluster bulletin Bulletin No 11 1-15 April 2009 Highlights: Cholera outbreak situation update • About 96, 473 cases and 4,204 deaths, CFR 4.4% Following a 9 week decline trend in cholera cases, an upsurge was reported during epidemi- • Sustained decline of ological week 15. Batch reporting in three districts may have contributed to this slight in- the outbreak crease. • Cholera hotspots in The cumulative number of Mashonaland west, Cholera in Zimbabwe reported cholera cases was Harare and Chitungwiza 17 Aug 08 to 11th April 09 96, 473 and 4204 deaths with 10,000 cities cumulative Case Fatality Rate 8,000 Cases Deaths (CFR) as of 4.4 as of 15 April. During week 15, a 17% de- 6,000 crease in cases and 5% in- 4,000 crease in deaths was re- Number ported. The crude CFR is 2.7% 2,000 compared to 2.9% of week 14 0 while the I-CFR is 1.8% com- pared to 2.7% of week 14. The w2 w4 w6 w8 w36 w38 w40 w42 w44 w46 w48 w50 w52 w10 w12 w14 CFR has been steadily de- weeks clined although the proportion of deaths in health facilities has increased compared to Cholera in Zimbabw e from 16 Nov 08 to 11th A pril 09 those reported in the commu- W eekly c rude and institutional c ase-fatality ratios 10 nity. CFR 9 This is probably an indication Inside this issue: 8 iCFR 7 of more people accessing 6 treatment and/or the increas- Cholera situation 1 5 ing role of other co- 4 morbidities presenting along- ORPs in cholera 2 3 management percent side cholera.
    [Show full text]
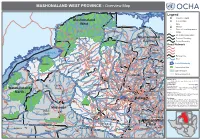
  • MASHONALAND WEST PROVINCE - Overview Map
    MASHONALAND WEST PROVINCE - Overview Map Kanyemba Mana Lake C. Bassa Pools Legend Province Capital Mashonaland Key Location r ive R Mine zi West Hunyani e Paul V Casembi b Chikafa Chidodo Mission Chirundu m Angwa Muzeza a Bridge Z Musengezi Place of Local Importance Rukomechi Masoka Mushumbi Musengezi Mbire Pools Chadereka Village Marongora St. International Boundary Cecelia Makuti Mashonaland Province Boundary Hurungwe Hoya Kaitano Kamuchikukundu Bwazi Chitindiwa Muzarabani District Boundary Shamrocke Bakasa Central St. St. Vuti Alberts Alberts Nembire KARIBA Kachuta Kazunga Chawarura Road Network Charara Lynx Centenary Dotito Kapiri Mwami Guruve Mount Lake Kariba Dora Shinje Masanga Centenary Darwin Doma Mount Maumbe Guruve Gachegache Darwin Railway Line Chalala Tashinga KAROI Kareshi Magunje Bumi Mudindo Bure River Hills Charles Mhangura Nyamhunga Clack Madadzi Goora Mola Mhangura Madombwe Chanetsa Norah Silverside Mutepatepa Bradley Zvipane Chivakanyama Madziwa Lake/Waterbody Kariba Nyakudya Institute Raffingora Jester Mvurwi Vanad Mujere Kapfunde Mudzumu Nzvimbo Shamva Conservation Area Kapfunde Feock Kasimbwi Madziwa Tengwe Siyakobvu Chidamoyo Muswewenhede Chakonda Msapakaruma Chimusimbe Mutorashanga Howard Other Province Negande Chidamoyo Nyota Zave Institute Zvimba Muriel Bindura Siantula Lions Freda & Mashonaland West Den Caesar Rebecca Rukara Mazowe Shamva Marere Shackleton Trojan Shamva Chete CHINHOYI Sutton Amandas Glendale Alaska Alaska BINDURA Banket Muonwe Map Doc Name: Springbok Great Concession Manhenga Tchoda Golden
    [Show full text]
  • “Bullets for Each of You” RIGHTS State-Sponsored Violence Since Zimbabwe’S March 29 Elections WATCH
    Zimbabwe HUMAN “Bullets for Each of You” RIGHTS State-Sponsored Violence since Zimbabwe’s March 29 Elections WATCH “Bullets for Each of You” State-Sponsored Violence since Zimbabwe’s March 29 Elections Copyright © 2008 Human Rights Watch All rights reserved. Printed in the United States of America ISBN: 1-56432-324-2 Cover design by Rafael Jimenez Human Rights Watch 350 Fifth Avenue, 34th floor New York, NY 10118-3299 USA Tel: +1 212 290 4700, Fax: +1 212 736 1300 [email protected] Poststraße 4-5 10178 Berlin, Germany Tel: +49 30 2593 06-10, Fax: +49 30 2593 0629 [email protected] Avenue des Gaulois, 7 1040 Brussels, Belgium Tel: + 32 (2) 732 2009, Fax: + 32 (2) 732 0471 [email protected] 64-66 Rue de Lausanne 1202 Geneva, Switzerland Tel: +41 22 738 0481, Fax: +41 22 738 1791 [email protected] 2-12 Pentonville Road, 2nd Floor London N1 9HF, UK Tel: +44 20 7713 1995, Fax: +44 20 7713 1800 [email protected] 27 Rue de Lisbonne 75008 Paris, France Tel: +33 (1)43 59 55 35, Fax: +33 (1) 43 59 55 22 [email protected] 1630 Connecticut Avenue, N.W., Suite 500 Washington, DC 20009 USA Tel: +1 202 612 4321, Fax: +1 202 612 4333 [email protected] Web Site Address: http://www.hrw.org June 2008 1-56432-324-2 “Bullets for Each of You” State-Sponsored Violence since Zimbabwe’s March 29 Elections I. Summary............................................................................................................... 1 II. Recommendations ...............................................................................................5 To the Government of Zimbabwe.........................................................................5 To the Movement for Democratic Change ..........................................................
    [Show full text]
  • NW Magondi Belt and Makuti Group, NW Zimbabwe Selected Roadside Exposures Between Karoi and Kariba 19 November 2015
    Geological Society of Zimbabwe, Annual Summer Symposium, Kariba, Zimbabwe, 20 November 2015 Field Excursion Guide- NW Magondi Belt and Makuti Group, NW Zimbabwe Selected roadside exposures between Karoi and Kariba 19 November 2015 Excursion Leaders: Sharad Master EGRI, School of Geosciences, University of the Witwatersrand, P. Bag 3, WITS 2050, Johannesburg, South Africa, [email protected] Tim Broderick [email protected] 1 November 2015 NW Magondi Belt and Makuti Group, NE Zimbabwe Selected roadside exposures between Karoi and Kariba Introduction The Magondi Belt is a Palaeoproterozoic mobile belt situated on the western flank of the Archaean Zimbabwe Craton, extending from NW Zimbabwe to NE Botswana. It consists of deformed rocks of the Palaeoproterozoic Magondi Supergroup, a 2.2-2.06 Ga metasedimentary succession with minor volcanic rocks (Master et al., 2010; 2013). On the eastern part of the belt, there are autochthonous units that are in unconformable contact with Archaean granite- greenstone rocks of the Zimbabwe Craton. In the north and northeast of the belt, Magondi Supergroup rocks apparently either overlie older basement gneisses and schists unconformably, or are found as infolds within such basement. In the northern part of the Magondi Belt, the crystalline basement consists of a heterogeneous succession of paragneisses and orthogneisses, which vary from foliated granitic leucogneisses to biotite gneisses to migmatites. There are also intercalations of hornblende-diopside calc-silicate gneisses. Granitoids consisting of plugs of granodioritic and tonalitic gneisses intrude the various paragneiss units. The paragneisses and their associated intrusive granitic orthogneisses and ortho-amphibolites record a major orogenic cycle, named the “Hurungwe Orogeny” (Master, 1991, 1996), that is imprecisely dated, but apparently predated the ca.
    [Show full text]
  • Zimbabwean Government Gazette
    V* A '’I ZIMBABWEAN GOVERNMENT GAZETTE Published by Authority Vol. LXXI, No. 31 14th MAY, 1993 Price $2,50 ► t General Notice 272 of 1993. The service to operate as follows— (a) dei^ Gweru Tuesday, Thursday and Sunday 6 a.m., ROAD MOTOR TRANSPORTATION ACT {CHAPTER 262] arrive Chiredzi 12.20 p.m.; (b) depart Chiredzi Monday, Wednesday and Friday 5 a.m., Application in Connexion with Road Service Permits arrive Gweru lr.41 a.m. Mucheche Investments (Pvt) Ltd. IN terms of subsection (4) of section 7 of the Road Motor 0/44/93. Permit; 25526. Passenger-capacity: 76. Transportation Act {Chapter 262], notice is hereby given that the applications detailed in the Schedule, for die issue or Route: Harare - 'Banket - Chinhoyi - lion’s Den - Karoi - amendment of road service permits, have been received for MagunM - Karereshi Business Centre - Mahororo Sdipol - the consideration of the Controller of Road Motor Trans­ Kanyati Business Centre - Birimahwe - Mangwaira - Buru- ruka Business Centre - Zvipani - Chiroti School - Chidamoyo. portation. Any person wishing to object to any such application must By: lodge with the Controller of Road Motor Trans^rtation, (a) Extension of route from CMdamoyo - Batanai - Oujawi P.O. Box 8332, Causeway— - Uroyi TownsMp. (a) a notice, in -writing, of his intention to object, so as (b) 'Deletion of interstages Banket and Lion’s Den and sub^ to reach the Controller’s office not later than the 4th Btitution of Kuwadrana TownsMp and Murereka Town­ June, 1993; sMp, respectively, (b) Ms objection and the grounds therefor, on form R.M.T. (c) Alteration of departure times on Friday and Sunday.
    [Show full text]
  • Contents Table
    EMBARGOED TILL END OF DELIVERY ZIMBABWE The 2011 National Budget Statement Shared Economy, Shared Development, Shared Transformation “Creating the Fair Economy” Presented to the Parliament of Zimbabwe on 25 November 2010 By Hon. T. Biti, M.P., Minister of Finance 1 Contents I. MOTION........................................................................................................................... 9 II. INTRODUCTION ............................................................................................................ 9 III. GLOBAL ECONOMIC DEVELOPMENTS & OUTLOOK ......................................... 15 OUTPUT ............................................................................................................................... 15 GLOBAL INFLATION ........................................................................................................... 16 INTERNATIONAL COMMODITY PRICES........................................................................... 17 OUTLOOK ............................................................................................................................ 18 IV. RECENT ECONOMIC DEVELOPMENTS .................................................................. 20 INFLATION .......................................................................................................................... 20 REAL SECTOR ..................................................................................................................... 21 Agriculture .....................................................................................................................
    [Show full text]
  • Map of Zimbabwe
    Cahora Bassa 28 Lusaka 30 32 Dam 34 ° ° Zumbo ° ° Kafue bezi Z Kafue am Cahora am Z Kanyemba b Mazabuka Albufeira de Bassa è Namwala z ZIMBABWE Cahora Bassa e 16° Chirundu 16° Monze Makuti i n MOZAMBIQUE Tete a Kariba y ZAMBIA n Kariba Dam u H MASHONALAND LakeKariba Centenary Mount Darwin Mulobezi Choma Karoi Mhangura Changara S e a o n CENTRAL z Z a a y MASHONALAND a M m Kalomo ti Zave b Kildonan Bindura Shamva e WEST z Masuku i Siabuwa TMutoko Glendale S Sesheke Maamba Chinhoyi A E D Kazungula Binga N Lake Harare A NAMIBIA Livingstone Manyame L obe Kasane Victoria A Ch M 18 ti Falls L. N 18 °n Victoria Falls Gokwe u Chitungwiza O Marondera Catandica ° ya ny Nyanga in Matetsi at Chegutu H L Kachikau Kamativi i S G Sengwa wa Kadoma A Hwange yi Rusape Pandamatenga Dahlia MHwedza Dete (Gwayi River Farms) Nyazura i S z hang d ani S O a Kwekwe v Lupane e Manica Redcliff Chivhu MIDLANDS Mutare MATABELELAND Mvuma Chimoio MANICALAND Lago R Eastnor Gweru Chicamba io NORTH M Hot Springs G Inyati Shurugwi w u BOTSWANA t Gutu a i y R r i i Chimanimani u k Nata n w Glenclova d i e Dombé Bulawayo 20 Birchenough i 20 ° Masvingo Chipinge z ° Nata Esigodini Lake Bridge u Zvishavane B Mutirikwi Rio e Plumtree v National capital a Espungabera S Provincial capital Mosetse MASVINGO Town, village Makgadikgadi Pan Antelope Gwanda Nandi Mill Major airport Mine Triangle S International boundary h West Nicholson Chiredzi Francistown a s R Provincial boundary h Rutenga u e n MATABELELAND Mbizi d U e Main road m E z U ZIMBABWE SOUTH in Makado Secondary road g IQ w M B a a Railroad n n M i is Thuli i A Z O 0 50 100 150 km Selebi-Pikwe Beitbridge M 22 Malvernia ° Limpopo Messina 0 50 100 mi o The boundaries and names shown and the designations op Limp SOUTH AFRICA used on this map do not imply official endorsement or 26° 28° acceptance by the United Nations.
    [Show full text]
  • District 412 Directory 2015 - 16
    We Care! We Serve! We Accomplish! DISTRICT 412 DIRECTORY 2015 - 16 ‘Excellence in Service’ ‘Dignity. Harmony. Humanity’ BOTSWANA MALAWI MOZAMBIQUE ZIMBABWE Contents Founder of Lionism 3 Lions Creed 4 Lions Pin 4 The International President 5 The DG Team 7 The Immediate Past International President 8 The Past International Director 9 History of Lionism in D412 10 District Officers 12 District Activity Chairpersons 15 Regional and Zone Chairpersons 21 Club President’s Installation Ceremony 26 New Member Induction Procedure 29 Club Officers 31 D412 Past Governors 44 The Honorary Committee 45 Founder Of Lionism Melvin Jones Lions have been helping people since 1917. That year, Melvin Jones, a Chicago businessman, encouraged his club, the Chicago Business Circle, to go beyond promoting good business practices. He convinced the members that selfless ser- vice to others would create a better community – and a better world – for all. Melvin Jones also saw that a network of clubs working together could do much more than individual clubs acting alone. He invited similar groups from around the United States to a meeting on June 7, 1917 in Chicago, Illinois, USA. There, the new group assumed the name of one of the invited clubs and the Association of Lions Clubs was born. Later that year, a convention was held in Dallas, Texas, USA to formally adopt a constitution, by-laws and a code of ethics. The fledg- ling group became the International Association of Lions Clubs just three years later when a new Lions club was formed in Windsor, Ontario, Canada. In the nearly 100 years since its founding, the association – usually called Lions Clubs International – has spread to all corners of the globe.
    [Show full text]
  • Dynamics of the Charcoal and Indigenous Timber Trade in Zambia a Scoping Study in Eastern, Northern and Northwestern Provinces
    OCCASIONAL PAPER Dynamics of the charcoal and indigenous timber trade in Zambia A scoping study in Eastern, Northern and Northwestern provinces Davison J. Gumbo Kaala B. Moombe Mercy M. Kandulu Gillian Kabwe Marja Ojanen Elizabeth Ndhlovu Terry C.H. Sunderland OCCASIONAL PAPER 86 Dynamics of the charcoal and indigenous timber trade in Zambia A scoping study in Eastern, Northern and Northwestern provinces Davison J. Gumbo CIFOR, Zambia Kaala B. Moombe CIFOR, Zambia Mercy M. Kandulu Forest Department Lusaka Province, Zambia Gillian Kabwe Copperbelt University, Zambia Marja Ojanen Finnish Embassy, Zambia Elizabeth Ndhlovu Finnish Embassy, Zambia Terry C. H. Sunderland CIFOR, Indonesia Occasional Paper 86 © 2013 Center for International Forestry Research All rights reserved ISBN 978-602-1504-02-4 Gumbo, D. J., Moombe, K. B., Kandulu, M. M., Kabwe, G., Ojanen, M., Ndhlovu, E. and Sunderland, T.C.H. 2013. Dynamics of the charcoal and indigenous timber trade in Zambia: A scoping study in Eastern, Northern and Northwestern provinces. Occasional Paper 86. CIFOR, Bogor, Indonesia. Cover photo by Terry Sunderland Photos by Davison Gumbo, except Figure 6 by Gillian Kabwe CIFOR Jl. CIFOR, Situ Gede Bogor Barat 16115 Indonesia T +62 (251) 8622-622 F +62 (251) 8622-100 E [email protected] cifor.org Any views expressed in this publication are those of the authors. They do not necessarily represent the views of CIFOR, the authors’ institutions or the financial sponsors of this publication. Table of contents Acknowledgements v Acronyms and abbreviations vi
    [Show full text]
  • Inter-Censal Demographic Survey 2017
    INTER-CENSAL DEMOGRAPHIC SURVEY, 2017 Zimbabwe ICDS 2017 Table of Contents Contents List of Tables .................................................................................................................................. v List of Figures ................................................................................................................................ ix Foreword ......................................................................................................................................... x Executive Summary ....................................................................................................................... xi Population Size and Structure..................................................................................................... xi Population Distribution............................................................................................................... xi Marital Status .............................................................................................................................. xi Ethnicity and Citizenship............................................................................................................ xi Religion ...................................................................................................................................... xi Disability Prevalence ................................................................................................................. xii Education and Literacy .............................................................................................................
    [Show full text]