Can Stellar Winds Account for Temperature Fluctuations in H II
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The HERACLES View of the H -To-HI Ratio in Galaxies
The HERACLES View of the H2-to-HI Ratio in Galaxies Adam Leroy (NRAO, Hubble Fellow) Fabian Walter, Frank Bigiel, the HERACLES and THINGS teams The Saturday Morning Summary • Star formation rate vs. gas relation on ~kpc scales breaks apart into: A relatively universal CO-SFR relation in nearby disks Systematic environmental scalings in the CO-to-HI ratio • The CO-to-HI ratio is a strong function of radius, total gas, and stellar surface density correlated with ISM properties: dust-to-gas ratio, pressure harder to link to dynamics: gravitational instability, arms • Interpretation: the CO-to-HI ratio traces the efficiency of GMC formation Density and dust can explain much of the observed behavior heracles Fabian Walter Erik Rosolowsky MPIA UBC Frank Bigiel Eva Schinnerer UC Berkeley THINGS plus… MPIA Elias Brinks Antonio Usero Gaelle Dumas U Hertfordshire OAN, Madrid MPIA Erwin de Blok Andreas Schruba Helmut Wiesemeyer U Cape Town IRAM … MPIA Rob Kennicutt Axel Weiss Karl Schuster Cambridge MPIfR IRAM Barry Madore Carsten Kramer Karin Sandstrom Carnegie IRAM MPIA Michele Thornley Daniela Calzetti Kelly Foyle Bucknell UMass MPIA Collaborators The HERA CO-Line Extragalactic Survey First maps Leroy et al. (2009) • IRAM 30m Large Program to map CO J = 2→1 line • Instrument: HERA receiver array operating at 230 GHz • 47 galaxies: dwarfs to starbursts and massive spirals -2 • Very wide-field (~ r25) and sensitive (σ ~ 1-2 Msun pc ) NGS The HI Nearby Galaxy Survey HI Walter et al. (2008), AJ Special Issue (2008) • VLA HI maps of 34 galaxies: -

Luminous Blue Variables
Review Luminous Blue Variables Kerstin Weis 1* and Dominik J. Bomans 1,2,3 1 Astronomical Institute, Faculty for Physics and Astronomy, Ruhr University Bochum, 44801 Bochum, Germany 2 Department Plasmas with Complex Interactions, Ruhr University Bochum, 44801 Bochum, Germany 3 Ruhr Astroparticle and Plasma Physics (RAPP) Center, 44801 Bochum, Germany Received: 29 October 2019; Accepted: 18 February 2020; Published: 29 February 2020 Abstract: Luminous Blue Variables are massive evolved stars, here we introduce this outstanding class of objects. Described are the specific characteristics, the evolutionary state and what they are connected to other phases and types of massive stars. Our current knowledge of LBVs is limited by the fact that in comparison to other stellar classes and phases only a few “true” LBVs are known. This results from the lack of a unique, fast and always reliable identification scheme for LBVs. It literally takes time to get a true classification of a LBV. In addition the short duration of the LBV phase makes it even harder to catch and identify a star as LBV. We summarize here what is known so far, give an overview of the LBV population and the list of LBV host galaxies. LBV are clearly an important and still not fully understood phase in the live of (very) massive stars, especially due to the large and time variable mass loss during the LBV phase. We like to emphasize again the problem how to clearly identify LBV and that there are more than just one type of LBVs: The giant eruption LBVs or h Car analogs and the S Dor cycle LBVs. -

Photo-Ionization Models of NGC 2363 and Their Implications
Wolf-Rayet Phenomena in Massive Stars and Starburst Galaxies Proceedings IAU Symposium No. 193, @1999 IAU K.A. van der Hucht, G. Koenigsberger f3 P.R.J. Eenens, eds. Photo-ionization models of NGC 2363 and their implications Valentina Luridiana and Manuel Peimbert Instituto de Astronomic, UNAM, Mexico Claus Leitherer Space Telescope Science Institute, Baltimore, MD, USA. Abstract. We compute photo-ionization models for the giant extragalactic H II region NGC 2363, and compare them with optical observational data. We focus on the following observational constraints: F(Hj3), Ni; EW(Hj3), and the ratios of I(A 5007), I(A 4363), I(A 3727), I(A 6300), I(A 6720) and I(A 4686) rel- ative to I(Hj3). We discuss the variations of the emission spectra obtained with different input parameters. We show that low metallicity models (Z == 0.10 Zev) cannot reproduce the observed features of the spectrum, and that the disagree- ment can be satisfactorily overcome by allowing for spatial temperature fluctu- ations in the nebula. Accordingly, we show that the metallicity of NGC 2363 has most probably been underestimated, and that a value of Z ~ 0.25 Zev is in better agreement with the observational data than the usually adopted value Z ~ 0.10 Zev. We also derive values for the slope and the high mass end of the IMF, as well as the age of the stellar cluster. 1. Introduction NGC 2363 is a very luminous giant H II region, located in the south-west end of the irregular galaxy NGC 2366. It is one of the brightest extragalactic H II re- 6 gions known, with an estimated mass of about 2.2 x 10 M0 (Carigi & Peimbert 1999). -
![Arxiv:1704.01678V2 [Astro-Ph.GA] 28 Jul 2017 Been Notoriously Difficult, Resulting Mostly in Upper Lim- Highest Escape Fractions Measured to Date Among Low- Its (E.G](https://docslib.b-cdn.net/cover/5778/arxiv-1704-01678v2-astro-ph-ga-28-jul-2017-been-notoriously-di-cult-resulting-mostly-in-upper-lim-highest-escape-fractions-measured-to-date-among-low-its-e-g-465778.webp)
Arxiv:1704.01678V2 [Astro-Ph.GA] 28 Jul 2017 Been Notoriously Difficult, Resulting Mostly in Upper Lim- Highest Escape Fractions Measured to Date Among Low- Its (E.G
Submitted: 3 March 2017 Preprint typeset using LATEX style AASTeX6 v. 1.0 MRK 71 / NGC 2366: THE NEAREST GREEN PEA ANALOG Genoveva Micheva1, M. S. Oey1, Anne E. Jaskot2, and Bethan L. James3 (Accepted 24 July 2017) 1University of Michigan, 311 West Hall, 1085 S. University Ave, Ann Arbor, MI 48109-1107, USA 2Department of Astronomy, Smith College, Northampton, MA 01063, USA 3STScI, 3700 San Martin Drive, Baltimore, MD 21218, USA ABSTRACT We present the remarkable discovery that the dwarf irregular galaxy NGC 2366 is an excellent analog of the Green Pea (GP) galaxies, which are characterized by extremely high ionization parameters. The similarities are driven predominantly by the giant H II region Markarian 71 (Mrk 71). We compare the system with GPs in terms of morphology, excitation properties, specific star-formation rate, kinematics, absorption of low-ionization species, reddening, and chemical abundance, and find consistencies throughout. Since extreme GPs are associated with both candidate and confirmed Lyman continuum (LyC) emitters, Mrk 71/NGC 2366 is thus also a good candidate for LyC escape. The spatially resolved data for this object show a superbubble blowout generated by mechanical feedback from one of its two super star clusters (SSCs), Knot B, while the extreme ionization properties are driven by the . 1 Myr-old, enshrouded SSC Knot A, which has ∼ 10 times higher ionizing luminosity. Very massive stars (> 100 M ) may be present in this remarkable object. Ionization-parameter mapping indicates the blowout region is optically thin in the LyC, and the general properties also suggest LyC escape in the line of sight. -

Cold Gas and Baryon-Induced Dark Matter Cores in Nearby Galaxies
Cold gas and baryon-induced dark matter cores in nearby galaxies Flor Allaert Supervisors: Prof. Dr. Maarten Baes, Dr. Gianfranco Gentile A dissertation submitted to Ghent University in partial fulfilment of the requirements for the degree of Doctor of Science: Astronomy September 2017 Supervisors: Prof. Dr. Maarten Baes Vakgroep Fysica en Sterrenkunde Universiteit Gent Dr. Gianfranco Gentile Vakgroep Fysica en Sterrenkunde Vrije Universiteit Brussel Jury members: Prof. Dr. Dirk Poelman (President) Vakgroep Vastestofwetenschappen Universiteit Gent Dr. Karel Van Acoleyen (Secretary) Vakgroep Fysica en Sterrenkunde Universiteit Gent Prof. Dr. Sven De Rijcke Vakgroep Fysica en Sterrenkunde Universiteit Gent Prof. Dr. Herwig Dejonghe Vakgroep Fysica en Sterrenkunde Universiteit Gent Prof. Dr. Uli Klein Argelander-Institut fur¨ Astronomie Universitat¨ Bonn Prof. Dr. Erwin de Blok Netherlands Institute for Radio Astronomy Contents 1 Introduction1 1.1 Galaxies - building blocks of the Universe.................1 1.1.1 Classification............................2 1.1.2 Chemical evolution.........................4 1.1.3 Accretion and mergers.......................6 1.2 Observing the different components....................8 1.2.1 Stars................................8 1.2.2 Gas.................................9 1.2.3 Dust................................. 12 1.3 Panchromatic SED modelling and dust radiative transfer......... 13 1.3.1 SED fitting............................. 13 1.3.2 Dust radiative transfer....................... 14 1.3.3 The energy balance problem.................... 15 1.4 FRIEDL, HEROES and NHEMESES................... 17 1.4.1 The energy balance problem revisited............... 18 1.5 Dark matter................................. 18 1.5.1 History............................... 19 1.5.2 Dark matter in cosmology..................... 21 1.5.3 Cosmological simulations..................... 23 1.5.4 The cusp-core controversy..................... 24 1.5.5 Baryons to the rescue?...................... -

Arxiv:Astro-Ph/0104091V1 4 Apr 2001 B .J Asnrsac Etr Obx28 Okonheight Yorktown 218, Box PO Center, Research Watson J
Neutral Hydrogen and Star Formation in the Irregular Galaxy NGC 2366 Deidre A. Hunter Lowell Observatory, 1400 West Mars Hill Road, Flagstaff, Arizona 86001 USA; [email protected] Bruce G. Elmegreen IBM T. J. Watson Research Center, PO Box 218, Yorktown Heights, New York 10598 USA; [email protected] and Hugo van Woerden Kapteyn Astronomical Institute, Postbus 800, 9700 AV Groningen, The Netherlands; [email protected] ABSTRACT We present deep UBVJHKHα images and HI maps of the irregular galaxy NGC 2366. Optically, NGC 2366 is a boxy-shaped exponential disk seen at high inclination angle. The scale length and central surface brightness of the disk are normal for late-type galaxies. Although NGC 2366 has been classified as a barred Im galaxy, we do not see any unambiguous observational signature of a bar. There is an asymmetrical extension of stars along one end of the major axis of the galaxy, and this is where the furthest star-forming regions are found, at a radius of 1.3 times the Holmberg radius. The star formation activity of the galaxy is dominated by the supergiant H ii complex NGC 2363, but the global star formation rate for NGC 2366 is only moderately elevated relative to other Im galaxies. The star formation activity drops off with radius arXiv:astro-ph/0104091v1 4 Apr 2001 approximately as the starlight in the inner part of the galaxy but it drops faster in the outer part. There are some peculiar features of the HI distribution and kinematics. First, the integrated HI shows two ridges running parallel to the major axis that when deprojected appear as a large ring. -
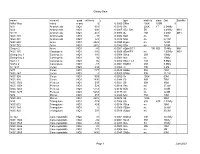
Galaxy Data Name Constell
Galaxy Data name constell. quadvel km/s z type width ly starsDist. Satellite Milky Way many many 0 0.0000 SBbc 106K 200M 0 M31 Andromeda NQ1 -301 -0.0010 SA 220K 1T 2.54Mly M32 Andromeda NQ1 -200 -0.0007 cE2 Sat. 5K 2.49Mly M31 M110 Andromeda NQ1 -241 -0.0008 dE 15K 2.69M M31 NGC 404 Andromeda NQ1 -48 -0.0002 SA0 no 10M NGC 891 Andromeda NQ1 528 0.0018 SAb no 27.3M NGC 680 Aries NQ1 2928 0.0098 E pec no 123M NGC 772 Aries NQ1 2472 0.0082 SAb no 130M Segue 2 Aries NQ1 -40 -0.0001 dSph/GC?. 100 5E5 114Kly MW NGC 185 Cassiopeia NQ1 -185 -0.0006dSph/E3 no 2.05Mly M31 Dwingeloo 1 Cassiopeia NQ1 110 0.0004 SBcd 25K 10Mly Dwingeloo 2 Cassiopeia NQ1 94 0.0003Iam no 10Mly Maffei 1 Cassiopeia NQ1 66 0.0002 S0pec E3 75K 9.8Mly Maffei 2 Cassiopeia NQ1 -17 -0.0001 SABbc 25K 9.8Mly IC 1613 Cetus NQ1 -234 -0.0008Irr 10K 2.4M M77 Cetus NQ1 1177 0.0039 SABd 95K 40M NGC 247 Cetus NQ1 0 0.0000SABd 50K 11.1M NGC 908 Cetus NQ1 1509 0.0050Sc 105K 60M NGC 936 Cetus NQ1 1430 0.0048S0 90K 75M NGC 1023 Perseus NQ1 637 0.0021 S0 90K 36M NGC 1058 Perseus NQ1 529 0.0018 SAc no 27.4M NGC 1263 Perseus NQ1 5753 0.0192SB0 no 250M NGC 1275 Perseus NQ1 5264 0.0175cD no 222M M74 Pisces NQ1 857 0.0029 SAc 75K 30M NGC 488 Pisces NQ1 2272 0.0076Sb 145K 95M M33 Triangulum NQ1 -179 -0.0006 SA 60K 40B 2.73Mly NGC 672 Triangulum NQ1 429 0.0014 SBcd no 16M NGC 784 Triangulum NQ1 0 0.0000 SBdm no 26.6M NGC 925 Triangulum NQ1 553 0.0018 SBdm no 30.3M IC 342 Camelopardalis NQ2 31 0.0001 SABcd 50K 10.7Mly NGC 1560 Camelopardalis NQ2 -36 -0.0001Sacd 35K 10Mly NGC 1569 Camelopardalis NQ2 -104 -0.0003Ibm 5K 11Mly NGC 2366 Camelopardalis NQ2 80 0.0003Ibm 30K 10M NGC 2403 Camelopardalis NQ2 131 0.0004Ibm no 8M NGC 2655 Camelopardalis NQ2 1400 0.0047 SABa no 63M Page 1 2/28/2020 Galaxy Data name constell. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -

National Gypsum Construction Guide
12TH EDITION 09 20 00/NGC National Gypsum Construction Guide ® HOW TO USE THE NATIONAL GYPSUM COMPANY GYPSUM CONSTRUCTION GUIDE NATIONAL GYPSUM PRODUCTS FOR ALL YOUR TRADEMARKS BUILDING NEEDS Your National Gypsum Company “Gypsum Construction The following names are trademarks owned by National Guide” has been carefully developed to provide you with a Gypsum Company or its subsidiary, National Gypsum comprehensive guide to the entire range of National Gypsum Properties, LLC: products. We have attempted to give you the most accurate, DURABASE® KAL-KOTE® up-to-date information in a clear, concise, easy-to-read DURASAN® KAL-MESH® format. Because it is important for us to ensure our guide is ® ® user-friendly, we welcome your comments. Please write EASY FINISH MULTI-FLEX us at: National Gypsum Company Technical Services EDGE GRIPTM NGC® Department, 2001 Rexford Road, Charlotte, N.C. 28211 or EXCELLENCE ACROSS 1-800 NATIONAL® ® call 1-800-NATIONAL (1-800-628-4662) U.S.A. or Canada. THE BOARD PERFECT SPRAY® 2 For your easy reference and accessibility to this information, we e XP™ PERMABASE® ® have placed all of our Sweet’s material in this section. For a E-Z STRIP PERMABASE FLEX® complete copy of our literature call 1-800-NATIONAL. ® FIRE-SHIELD PROFORM® TM FIRE-SHIELD C SEASPRAY MVR® CAD DRAWINGS AND SPECIFICATIONS ® GOLD BOND SHAFTLINER® ® To assist you in your design process, all CAD drawings and GOLD BOND 54 SHAFTLINER XP® specifications are available at www.nationalgypsum.com. ® GRIDMARX SOUNDBREAK™ Computer aided design (CAD) drawings are in DXF, DWG and ® GRIDSTONE STA-SMOOTH® GIF file formats. -

1 I Articles Dans Des Revues Avec Comité De Lecture
1 I Articles dans des revues avec comité de lecture (ACL) internationales II Articles dans des revues sans comité de lecture (SCL) NB : La liste des publications est donnée de façon exhautive par équipe, ce qui signifie qu’il existe des redondances chaque fois qu’une publication est cosignée pas des membres dépendant d’équipes différentes. Par contre, certains chercheurs sont à cheval sur deux équipes, dans ce cas il leur a été demandé de rattacher leurs publications seulement à l’une ou à l’autre équipe en fonction de la nature de la publication et la raison de leur rattachement à deux équipes. I Articles dans des revues avec comité de lecture (ACL) internationales ANNÉE 2006 A / Equipe « Physique des galaxies » 1. Aguilar, J.A. et al. (the ANTARES collaboration, 214 auteurs). First results of the Instrumentation Line for the deep- sea ANTARES neturino telescope Astroparticle Physic 26, 314 2. Auld, R.; Minchin, R. F.; Davies, J. I.; Catinella, B.; van Driel, W.; Henning, P. A.; Linder, S.; Momjian, E.; Muller, E.; O'Neil, K.; Boselli, A.; et 18 coauteurs. The Arecibo Galaxy Environment Survey: precursor observations of the NGC 628 group, 2006, MNRAS,.371,1617A 3. Boselli, A.; Boissier, S.; Cortese, L.; Gil de Paz, A.; Seibert, M.; Madore, B. F.; Buat, V.; Martin, D. C. The Fate of Spiral Galaxies in Clusters: The Star Formation History of the Anemic Virgo Cluster Galaxy NGC 4569, 2006, ApJ, 651, 811B 4. Boselli, A.; Gavazzi, G. Environmental Effects on Late-Type Galaxies in Nearby Clusters -2006, PASP, 118, 517 5. -

First Results from the MADCASH Survey: a Faint Dwarf Galaxy
Draft version August 10, 2016 Preprint typeset using LATEX style AASTeX6 v. 1.0 FIRST RESULTS FROM THE MADCASH SURVEY: A FAINT DWARF GALAXY COMPANION TO THE LOW MASS SPIRAL GALAXY NGC 2403 AT 3.2 MPC 1 Jeffrey L. Carlin2, David J. Sand3, Paul Price4, Beth Willman2, Ananthan Karunakaran5, Kristine Spekkens5,6, Eric F. Bell7, Jean P. Brodie8, Denija Crnojevic´3, Duncan A. Forbes9, Jonathan Hargis10, Evan Kirby11, Robert Lupton4, Annika H. G. Peter12, Aaron J. Romanowsky8, 13, and Jay Strader14 1Based in part on data collected at Subaru Telescope, which is operated by the National Astronomical Observatory of Japan. 2LSST and Steward Observatory, 933 North Cherry Avenue, Tucson, AZ 85721, USA; Haverford College, Department of Astronomy, 370 Lancaster Avenue, Haverford, PA 19041, USA; jeff[email protected] 3Texas Tech University, Physics Department, Box 41051, Lubbock, TX 79409-1051, USA 4Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA 5Department of Physics, Engineering Physics and Astronomy, Queen’s University, Kingston, Ontario, Canada, K7L 3N6 6Department of Physics, Royal Military College of Canada, P.O. Box 17000, Station Forces, Kingston, ON K7L 7B4, Canada 7Department of Astronomy, University of Michigan, 1085 South University Ave, Ann Arbor, MI 48109, USA 8University of California Observatories, 1156 High Street, Santa Cruz, CA 95064, USA 9Centre for Astrophysics and Supercomputing, Swinburne University, Hawthorn VIC 3122, Australia 10Space Telescope Science Institute, 3700 San Martin Drive, -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it.