DOCSLIB.ORG

A Thesis Submitted to the Faculty of San Francisco State University in Partial

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Thesis Submitted to the Faculty of San Francisco State University in Partial RESEARCH ON NAGOYA RESIDENTS’ CONSCIOUSNESS ABOUT THEIR REGIONAL DIALECTS AND DIALECTICAL USAGE A thesis submitted to the faculty of As San Francisco State University 36 In partial fulfillment of 2015" The requirements for The Degree Master of Arts In Japanese by Eriko Matsuura San Francisco, California May, 2015 Copyright by Eriko Matsuura 2015 CERTIFICATION OF APPROVAL I certify that I have read RESEARCH ON NAGOYA REGIDENTS’ CONSCIOUSNESS ABOUT THEIR REGIONAL DIALECTS AND DIALECTICAL USAGE by Eriko Matsuura, and that in my opinion this work meets the criteria for approving a thesis submitted in partial fulfillment of the requirement for the degree Master of Arts in Japanese at San Francisco State University. Professor of Japanese Dr. Makiko Asano Professor of Japanese RESEARCH ON NAGOYA REGIDENTS’ CONSCIOUSNESS ABOUT THEIR REGIONAL DIALECTS AND DIALECTICAL USAGE Eriko Matsuura San Francisco, California 2015 In recent years, the diversity of regions in Japan has attracted considerable attention. There are many opportunities to be exposed to different dialects through the dialect-related books and media. However, it is questionable how much dialect is really used and recognized in daily life. To investigate the current use of Nagoya dialect in the region, this survey was carried out in Nagoya-city and the Owari region of Aichi Prefecture, Japan. It was conducted using data was gathered from December 2013 to July 2014 from 741 Aichi residents (age 20 to 75). The research reports (1) how Nagoya dialect is evaluated by Nagoya residents, (2) How the evaluation of dialect influences dialect use, and (3) how the Nagoya dialect vocabulary, introduced in dialect publication, is used and recognized by Nagoya dialect speakers. I certifV that the Abstract is a correct representation of the content of this thesis. Date ACKNOWLEDGEMENTS I would like to express my deepest appreciation to my thesis adviser, Dr. Masahiko Minami for spending countless hours reading my drafts and giving me concrete feedback. This thesis would not have been possible without his advice and support. I would also like to recognize Dr. Makiko Asano for offering invaluable editing and advice. Her guidance was helpful in making my thesis successful. I would like to thank my parents, who have been supporting my education in the United States and have provided great encouragement. Finally, I would like to acknowledge my husband, who supported me and provided understanding throughout my courses at San Francisco State University. TABLE OF CONTENTS List of Tables...................................................................................................................... ix List of Figures...................................................................................................................... x List of Appendices..............................................................................................................xi 1. Introduction..................................................................................................................... 2 2. Literature Review............................................................................................................ 3 3. Methodology.................................................................................................................... 4 3.1. Survey research and recruitment of participants..............................................4 3.2. Questionnaire.................................................................................................... 5 3.2.1. Contents of personal data sheet..............................................................5 3.2.2. Contents of questions for participants....................................................6 3.3. Participants’ gender and age.............................................................................6 3.4. Participants’ birthplace and place of residence................................................7 4. Results............................................................................................................................. 8 4.1. Impression and evaluation of Nagoya dialect................................................9 4.1.1. Is Nagoya dialect urbane or rustic?........................................................9 4.1.2. Is Nagoya dialect clean or foul?........................................................... 10 4.1.3. Do you like or dislike Nagoya dialect?................................................ 12 4.2. Usage of Nagoya dialect in different situations............................................. 14 4.2.1. Usage of Nagoya dialect (Family members)....................................... 14 4.2.2. Usage of Nagoya dialect (Friends from the same region).................. 16 4.2.3. Usage of Nagoya dialect (Friends from different regions).................. 17 4.3. Usage of Nagoya dialect in different situations (with strangers)................... 18 4.3.1. Changing speech style......................................................................... 18 4.4. Thoughts for Nagoya dialect..........................................................................24 4.4.1. Preservation of Nagoya dialect.............................................................24 4.2.2. Arguments for and against the preservation of Nagoya dialect............25 4.5. Residents’ experience and knowledge of Nagoya dialect..............................29 4.6. Format of questionnaire..................................................................................30 4.7. Nagoya dialect speakers’ usage and knowledge of Nagoya dialect...............31 4.7.1. Changes in dialect usage and recognition by different generations 31 4.7.2. Is dialect usage declining?....................................................................31 4.7.3. Changing dialect vocabulary impressions and roles............................32 4.7.4. Changes in honorific speech.................................................................34 5. Discussion.................................................................................................................... 38 5.1. Current impressions and evaluations of Nagoya dialect..................................38 5.1. Factors affecting impressions and evaluations of Nagoya dialect............ 39 5.2. Current state of dialect usage...........................................................................39 5.2.1. Young generations’ preference for dialect.............................................40 5.2.2. Elder generations’ preference for standard Japanese.............................41 5.3. Roles and functions of dialects.................................................................................42 5.3.1. Role as a mother tongue.......................................................................42 5.3.2. Role as a communication tool..............................................................43 5.3.3. Role of transmitting the culture............................................................44 6. Conclusion................................................................................................................... 44 Appendices........................................................................................................................ 46 References......................................................................................................................... 56 English Summary..............................................................................................................59 viii LIST OF TABLES Tables Page 1. Result of chi-square “Is Nagoya dialect urbane or rustic?” ...........................10 2. Result of chi-square “Is Nagoya dialect clean or foul?” ................................11 3. Result of chi-square “Do you like or dislike Nagoya dialect?” .....................12 4. Result of chi-square: usage of Nagoya dialect (with family members).........14 5. Result of chi-square: usage of Nagoya dialect (friends from the same region) 16 6. Result of chi-square: usage of Nagoya dialect (friends from different regions)........................................................................................................... 17 7. Result of chi-square: Changing speech style...................................................19 8. Reasons to change speech style..................................................................... 20 9. Reasons not to change speech style................................................................22 10. Result of chi-square “Do you think Nagoya dialect should not be spoken?” ........................................................................................................................25 11. Reasons Nagoya dialect should not be spoken..........................................26 12. Reasons Nagoya dialect should be spoken................................................ 28 13. Nagoya dialect vocabulary and their meaning in standard-Japanese.............30 14. Result of chi-square: [-namo; ~right?]...........................................................32 15. Result of chi-square: \yattokame; long time no see]....................................... 33 16. Result of chi-square: [niisama; an older brother]............................................35 17. Result of chi-square: [ototo; a younger brother]..............................................36 18. Result of chi-square: [ossama\ a monk]........................................................... 37 LIST OF FIGURES Figures Page 1. Public announcement poster
Load more

Recommended publications
  • Week 1: an Overview of Circuit Complexity 1 Welcome 2
    Topics in Circuit Complexity (CS354, Fall’11) Week 1: An Overview of Circuit Complexity Lecture Notes for 9/27 and 9/29 Ryan Williams 1 Welcome The area of circuit complexity has a long history, starting in the 1940’s. It is full of open problems and frontiers that seem insurmountable, yet the literature on circuit complexity is fairly large. There is much that we do know, although it is scattered across several textbooks and academic papers. I think now is a good time to look again at circuit complexity with fresh eyes, and try to see what can be done. 2 Preliminaries An n-bit Boolean function has domain f0; 1gn and co-domain f0; 1g. At a high level, the basic question asked in circuit complexity is: given a collection of “simple functions” and a target Boolean function f, how efficiently can f be computed (on all inputs) using the simple functions? Of course, efficiency can be measured in many ways. The most natural measure is that of the “size” of computation: how many copies of these simple functions are necessary to compute f? Let B be a set of Boolean functions, which we call a basis set. The fan-in of a function g 2 B is the number of inputs that g takes. (Typical choices are fan-in 2, or unbounded fan-in, meaning that g can take any number of inputs.) We define a circuit C with n inputs and size s over a basis B, as follows. C consists of a directed acyclic graph (DAG) of s + n + 2 nodes, with n sources and one sink (the sth node in some fixed topological order on the nodes).
    [Show full text]
  • Japanese Native Speakers' Attitudes Towards
    JAPANESE NATIVE SPEAKERS’ ATTITUDES TOWARDS ATTENTION-GETTING NE OF INTIMACY IN RELATION TO JAPANESE FEMININITIES THESIS Presented in Partial Fulfillment of the Requirements for The Degree Master of Arts in the Graduate School of The Ohio State University By Atsuko Oyama, M.E. * * * * * The Ohio State University 2008 Master’s Examination Committee: Approved by Professor Mari Noda, Advisor Professor Mineharu Nakayama Advisor Professor Kathryn Campbell-Kibler Graduate Program in East Asian Languages and Literatures ABSTRACT This thesis investigates Japanese people’s perceptions of the speakers who use “attention-getting ne of intimacy” in discourse in relation to femininity. The attention- getting ne of intimacy is the particle ne that is used within utterances with a flat or a rising intonation. It is commonly assumed that this attention-getting ne is frequently used by children as well as women. Feminine connotations attached to this attention-getting ne when used by men are also noted. The attention-getting ne of intimacy is also said to connote both intimate and over-friendly impressions. On the other hand, recent studies on Japanese femininity have proposed new images that portrays figures of immature and feminine women. Assuming the similarity between the attention-getting ne and new images of Japanese femininity, this thesis aims to reveal the relationship between them. In order to investigate listeners’ perceptions of women who use the attention- getting ne of intimacy with respect to femininity, this thesis employs the matched-guise technique as its primary methodological choice using the presence of attention-getting ne of intimacy as its variable. In addition to the implicit reactions obtained in the matched- guise technique, people’s explicit thoughts regarding being onnarashii ‘womanly’ and kawairashii ‘endearing’ were also collected in the experiment.
    [Show full text]
  • The Complexity Zoo
    The Complexity Zoo Scott Aaronson www.ScottAaronson.com LATEX Translation by Chris Bourke [email protected] 417 classes and counting 1 Contents 1 About This Document 3 2 Introductory Essay 4 2.1 Recommended Further Reading ......................... 4 2.2 Other Theory Compendia ............................ 5 2.3 Errors? ....................................... 5 3 Pronunciation Guide 6 4 Complexity Classes 10 5 Special Zoo Exhibit: Classes of Quantum States and Probability Distribu- tions 110 6 Acknowledgements 116 7 Bibliography 117 2 1 About This Document What is this? Well its a PDF version of the website www.ComplexityZoo.com typeset in LATEX using the complexity package. Well, what’s that? The original Complexity Zoo is a website created by Scott Aaronson which contains a (more or less) comprehensive list of Complexity Classes studied in the area of theoretical computer science known as Computa- tional Complexity. I took on the (mostly painless, thank god for regular expressions) task of translating the Zoo’s HTML code to LATEX for two reasons. First, as a regular Zoo patron, I thought, “what better way to honor such an endeavor than to spruce up the cages a bit and typeset them all in beautiful LATEX.” Second, I thought it would be a perfect project to develop complexity, a LATEX pack- age I’ve created that defines commands to typeset (almost) all of the complexity classes you’ll find here (along with some handy options that allow you to conveniently change the fonts with a single option parameters). To get the package, visit my own home page at http://www.cse.unl.edu/~cbourke/.
    [Show full text]
  • Lower Bounds from Learning Algorithms
    Circuit Lower Bounds from Nontrivial Learning Algorithms Igor C. Oliveira Rahul Santhanam Charles University in Prague University of Oxford Motivation and Background Previous Work Lemma 1 [Speedup Phenomenon in Learning Theory]. From PSPACE BPTIME[exp(no(1))], simple padding argument implies: DSPACE[nω(1)] BPEXP. Some connections between algorithms and circuit lower bounds: Assume C[poly(n)] can be (weakly) learned in time 2n/nω(1). Lower bounds Lemma [Diagonalization] (3) (the proof is sketched later). “Fast SAT implies lower bounds” [KL’80] against C ? Let k N and ε > 0 be arbitrary constants. There is L DSPACE[nω(1)] that is not in C[poly]. “Nontrivial” If Circuit-SAT can be solved efficiently then EXP ⊈ P/poly. learning algorithm Then C-circuits of size nk can be learned to accuracy n-k in Since DSPACE[nω(1)] BPEXP, we get BPEXP C[poly], which for a circuit class C “Derandomization implies lower bounds” [KI’03] time at most exp(nε). completes the proof of Theorem 1. If PIT NSUBEXP then either (i) NEXP ⊈ P/poly; or 0 0 Improved algorithmic ACC -SAT ACC -Learning It remains to prove the following lemmas. upper bounds ? (ii) Permanent is not computed by poly-size arithmetic circuits. (1) Speedup Lemma (relies on recent work [CIKK’16]). “Nontrivial SAT implies lower bounds” [Wil’10] Nontrivial: 2n/nω(1) ? (Non-uniform) Circuit Classes: If Circuit-SAT for poly-size circuits can be solved in time (2) PSPACE Simulation Lemma (follows [KKO’13]). 2n/nω(1) then NEXP ⊈ P/poly. SETH: 2(1-ε)n ? ? (3) Diagonalization Lemma [Folklore].
    [Show full text]
  • A Superpolynomial Lower Bound on the Size of Uniform Non-Constant-Depth Threshold Circuits for the Permanent
    A Superpolynomial Lower Bound on the Size of Uniform Non-constant-depth Threshold Circuits for the Permanent Pascal Koiran Sylvain Perifel LIP LIAFA Ecole´ Normale Superieure´ de Lyon Universite´ Paris Diderot – Paris 7 Lyon, France Paris, France [email protected] [email protected] Abstract—We show that the permanent cannot be computed speak of DLOGTIME-uniformity), Allender [1] (see also by DLOGTIME-uniform threshold or arithmetic circuits of similar results on circuits with modulo gates in [2]) has depth o(log log n) and polynomial size. shown that the permanent does not have threshold circuits of Keywords-permanent; lower bound; threshold circuits; uni- constant depth and “sub-subexponential” size. In this paper, form circuits; non-constant depth circuits; arithmetic circuits we obtain a tradeoff between size and depth: instead of sub-subexponential size, we only prove a superpolynomial lower bound on the size of the circuits, but now the depth I. INTRODUCTION is no more constant. More precisely, we show the following Both in Boolean and algebraic complexity, the permanent theorem. has proven to be a central problem and showing lower Theorem 1: The permanent does not have DLOGTIME- bounds on its complexity has become a major challenge. uniform polynomial-size threshold circuits of depth This central position certainly comes, among others, from its o(log log n). ]P-completeness [15], its VNP-completeness [14], and from It seems to be the first superpolynomial lower bound on Toda’s theorem stating that the permanent is as powerful the size of non-constant-depth threshold circuits for the as the whole polynomial hierarchy [13].
    [Show full text]
  • ECC 2015 English
    © Springer-Verlag 2015 SpringerMedizin.at/memo_inoncology SpringerMedizin.at 2/15 /memo_inoncology memo – inOncology SPECIAL ISSUE Congress Report ECC 2015 A GLOBAL CONGRESS DIGEST ON NSCLC Report from the 18th ECCO- 40th ESMO European Cancer Congress, Vienna 25th–29th September 2015 Editorial Board: Alex A. Adjei, MD, PhD, FACP, Roswell Park, Cancer Institute, New York, USA Wolfgang Hilbe, MD, Departement of Oncology, Hematology and Palliative Care, Wilhelminenspital, Vienna, Austria Massimo Di Maio, MD, National Institute of Tumor Research and Th erapy, Foundation G. Pascale, Napoli, Italy Barbara Melosky, MD, FRCPC, University of British Columbia and British Columbia Cancer Agency, Vancouver, Canada Robert Pirker, MD, Medical University of Vienna, Vienna, Austria Yu Shyr, PhD, Department of Biostatistics, Biomedical Informatics, Cancer Biology, and Health Policy, Nashville, TN, USA Yi-Long Wu, MD, FACS, Guangdong Lung Cancer Institute, Guangzhou, PR China Riyaz Shah, PhD, FRCP, Kent Oncology Centre, Maidstone Hospital, Maidstone, UK Filippo de Marinis, MD, PhD, Director of the Th oracic Oncology Division at the European Institute of Oncology (IEO), Milan, Italy Supported by Boehringer Ingelheim in the form of an unrestricted grant IMPRESSUM/PUBLISHER Medieninhaber und Verleger: Springer-Verlag GmbH, Professional Media, Prinz-Eugen-Straße 8–10, 1040 Wien, Austria, Tel.: 01/330 24 15-0, Fax: 01/330 24 26-260, Internet: www.springer.at, www.SpringerMedizin.at. Eigentümer und Copyright: © 2015 Springer-Verlag/Wien. Springer ist Teil von Springer Science + Business Media, springer.at. Leitung Professional Media: Dr. Alois Sillaber. Fachredaktion Medizin: Dr. Judith Moser. Corporate Publishing: Elise Haidenthaller. Layout: Katharina Bruckner. Erscheinungsort: Wien. Verlagsort: Wien. Herstellungsort: Linz. Druck: Friedrich VDV, Vereinigte Druckereien- und Verlags-GmbH & CO KG, 4020 Linz; Die Herausgeber der memo, magazine of european medical oncology, übernehmen keine Verantwortung für diese Beilage.
    [Show full text]
  • Lecture 10: Logspace Division and Its Consequences 1. Overview
    IAS/PCMI Summer Session 2000 Clay Mathematics Undergraduate Program Advanced Course on Computational Complexity Lecture 10: Logspace Division and Its Consequences David Mix Barrington and Alexis Maciel July 28, 2000 1. Overview Building on the last two lectures, we complete the proof that DIVISION is in FOMP (first-order with majority quantifiers, BIT, and powering modulo short numbers) and thus in both L-uniform TC0 and L itself. We then examine the prospects for improving this result by putting DIVISION in FOM or truly uniform TC0, and look at some consequences of the L-uniform result for complexity classes with sublogarithmic space. We showed last time that we can divide a long number by a nice long number, • that is, a product of short powers of distinct primes. We also showed that given any Y , we can find a nice number D such that Y=2 D Y . We finish the proof by finding an approximation N=A for D=Y , where≤ A ≤is nice, that is good enough so that XN=AD is within one of X=Y . b c We review exactly how DIVISION, ITERATED MULTIPLICATION, and • POWERING of long integers (poly-many bits) are placed in FOMP by this argument. We review the complexity of powering modulo a short integer, and consider • how this affects the prospects of placing DIVISION and the related problems in FOM. Finally, we take a look at sublogarithmic space classes, in particular problems • solvable in space O(log log n). These classes are sensitive to the definition of the model. We argue that the more interesting classes are obtained by marking the space bound in the memory before the machine starts.
    [Show full text]
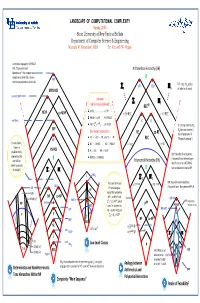
  • LANDSCAPE of COMPUTATIONAL COMPLEXITY Spring 2008 State University of New York at Buffalo Department of Computer Science & Engineering Mustafa M
    LANDSCAPE OF COMPUTATIONAL COMPLEXITY Spring 2008 State University of New York at Buffalo Department of Computer Science & Engineering Mustafa M. Faramawi, MBA Dr. Kenneth W. Regan A complete language for EXPSPACE: PIM, “Polynomial Ideal Arithmetical Hierarchy (AH) Membership”—the simplest natural completeness level that is known PIM not to have polynomial‐size circuits. TOT = {M : M is total, K(2) TOT e e ∑n Πn i.e. halts for all inputs} EXPSPACE Succinct 3SAT Unknown ∑2 Π2 but Commonly Believed: RECRE L ≠ NL …………………….. L ≠ PH NEXP co‐NEXP = ∃∀.REC = ∀∃.REC P ≠ NP ∩ co‐NP ……… P ≠ PSPACE nxn Chess p p K D NP ≠ ∑ 2 ∩Π 2 ……… NP ≠ EXP D = {Turing machines M : EXP e Best Known Separations: Me does not accept e} = RE co‐RE the complement of K. AC0 ⊂ ACC0 ⊂ PP, also TC0 ⊂ PP QBF REC (“Diagonal Language”) For any fixed k, NC1 ⊂ PSPACE, …, NL ⊂ PSPACE = ∃.REC = ∀.REC there is a PSPACE problem in this P ⊂ EXP, NP ⊂ NEXP BQP: Bounded‐Error Quantum intersection that PSPACE ⊂ EXPSPACE Polynomial Time. Believed larger can NOT be Polynomial Hierarchy (PH) than P since it has FACTORING, solved by circuits p p k but not believed to contain NP. of size O(n ) ∑ 2 Π 2 L WS5 p p ∑ 2 Π 2 The levels of AH and poly. poly. BPP: Bounded‐Error Probabilistic TAUT = ∃∀ P = ∀∃ P SAT Polynomial Time. Many believe BPP = P. NC1 PH are analogous, NLIN except that we believe NP co‐NP 0 NP ∩ co‐NP ≠ P and NTIME [n2] TC QBF PARITY ∑p ∩Πp NP PP Probabilistic NP FACT 2 2 ≠ P , which NP ACC0 stand in contrast to P PSPACE Polynomial Time MAJ‐SAT CVP RE ∩ co‐RE = REC and 0 AC RE P P ∑2 ∩Π2 = REC GAP NP co‐NP REG NL poly 0 0 ∃ .
    [Show full text]
  • Optimally Sound Sigma Protocols Under DCRA
    Optimally Sound Sigma Protocols Under DCRA Helger Lipmaa University of Tartu, Tartu, Estonia Abstract. Given a well-chosen additively homomorphic cryptosystem and a Σ protocol with a linear answer, Damg˚ard,Fazio, and Nicolosi proposed a non-interactive designated-verifier zero knowledge argument in the registered public key model that is sound under non-standard complexity-leveraging assumptions. In 2015, Chaidos and Groth showed how to achieve the weaker yet reasonable culpable soundness notion un- der standard assumptions but only if the plaintext space order is prime. It makes use of Σ protocols that satisfy what we call the optimal culpable soundness. Unfortunately, most of the known additively homomorphic cryptosystems (like the Paillier Elgamal cryptosystem that is secure un- der the standard Decisional Composite Residuosity Assumption) have composite-order plaintext space. We construct optimally culpable sound Σ protocols and thus culpably sound non-interactive designated-verifier zero knowledge protocols for NP under standard assumptions given that the least prime divisor of the plaintext space order is large. Keywords: Culpable soundness, designated verifier, homomorphic en- cryption, non-interactive zero knowledge, optimal soundness, registered public key model 1 Introduction Non-interactive zero knowledge (NIZK, [8]) proof system enable the prover to convince the verifier in the truth of a statement without revealing any side in- formation. Unfortunately, it is well known that NIZK proof systems are not secure in the standard model. Usually, this means that one uses the random oracle model [6] or the common reference string (CRS, [8]) model. In particular, Σ protocols [14] can be efficiently transformed into NIZK proof systems in the random oracle model by using the Fiat-Shamir heuristic [21].
    [Show full text]
  • Propositional Proof Complexity Past Present and Future
    Prop ositional Pro of Complexity Past Present and Future Paul Beame and Toniann Pitassi Abstract Pro of complexity the study of the lengths of pro ofs in prop ositional logic is an area of study that is fundamentally connected b oth to ma jor op en questions of computational complexity theory and to practical prop erties of automated theorem provers In the last decade there have b een a number of signicant advances in pro of complexity lower b ounds Moreover new connections b etween pro of complexity and circuit complexity have b een uncovered and the interplay b etween these two areas has b ecome quite rich In addition attempts to extend existing lower b ounds to ever stronger systems of pro of have spurred the introduction of new and interesting pro of systems adding b oth to the practical asp ects of pro of complexity as well as to a rich theory This note attempts to survey these developments and to lay out some of the op en problems in the area Introduction One of the most basic questions of logic is the following Given a uni versally true statement tautology what is the length of the shortest pro of of the statement in some standard axiomatic pro of system The prop osi tional logic version of this question is particularly imp ortant in computer science for b oth theorem proving and complexity theory Imp ortant related algorithmic questions are Is there an ecient algorithm that will pro duce a pro of of any tautology Is there an ecient algorithm to pro duce the shortest pro of of any tautology Such questions of theorem proving and
    [Show full text]
  • Cosmology and Complexity 325
    more information - www.cambridge.org/9780521199568 http://youtu.be/f477FnTe1M0 http://youtu.be/4qAIPC7vG3Y Quantum Computing since Democritus Written by noted quantum computing theorist Scott Aaronson, this book takes readers on a tour through some of the deepest ideas of math, computer science, and physics. Full of insights, arguments, and philosophical perspectives, the book covers an amazing array of topics. Beginning in antiquity with Democritus, it progresses through logic and set theory, computability and complexity theory, quantum computing, cryptography, the information content of quantum states, and the interpretation of quantum mechanics. There are also extended discussions about time travel, Newcomb’s Paradox, the Anthropic Principle, and the views of Roger Penrose. Aaronson’s informal style makes this fascinating book accessible to readers with scientific backgrounds, as well as students and researchers working in physics, computer science, mathematics, and philosophy. scott aaronson is an Associate Professor of Electrical Engineering and Computer Science at the Massachusetts Institute of Technology. Considered one of the top quantum complexity theorists in the world, he is well known both for his research in quantum computing and computational complexity theory, and for his widely read blog Shtetl-Optimized. Professor Aaronson also created Complexity Zoo, an online encyclopedia of computational complexity theory, and has written popular articles for Scientific American and The New York Times. His research and popular writing
    [Show full text]
  • Uhm Phd 4350 R.Pdf
    UNIVERSITY OF HAWAI'! LIBRARY EMERGENT PROPERTIES OF JAPANESE VERBAL INFLECTION A DISSERTATION SUBMITTED TO THE GRADUATE DIVISION OF THE UNIVERSITY OF HAWAI'I IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY IN LINGUISTICS AUGUST 2003 By Terry Klafehn Dissertation Committee: Ann M. Peters, Chair Niklaus R. Schweizer John H. Haig William D. O'Grady Benjamin K. Bergen © Copyright 2003 By Terry Klafehn iii ACKNOWLEDGEMENTS There are a number ofpeople I wish to thank for making this dissertation possible. I could not have completed my research and writing without their assistance, professional and technical expertise, and warm encouragement. First of all there is my wife Sharyn, who patiently urged me to keep going when I was discouraged and overwhelmed by the task. I wish to thank my friend Mr. Kazuki Daimon, president of the International Sports Education and Cultural Foundation (ISEC Japan), for making arrangements in Japan so that I was able to conduct research at the Ushigomi Nakano Kindergarten in Shinjuku. My friend Jeffrey Hayden from the EALL department spent many long hours preparing the computerized test that I used with the Japanese children. He continues to patiently help me with computer problems. Wendy Onishi from the office of the Department of Linguistics processed any number of important documents (including a number of extensions) for me in a timely manner. Her "Well, are we making progress?" was more encouraging than she realizes. Evelyn Nakanishi, student services specialist at EALL was always willing to listen to my complaints, offer some encouragement, and conclude our conversation with the friendly admonition "Get back to work!" Stan Starosta made a very important contribution this dissertation.
    [Show full text]