BO1 History of Mathematics Lecture VII Infinite Series Part 1: a Non
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Particulars of Some Temples of Kerala Contents Particulars of Some
Particulars of some temples of Kerala Contents Particulars of some temples of Kerala .............................................. 1 Introduction ............................................................................................... 9 Temples of Kerala ................................................................................. 10 Temples of Kerala- an over view .................................................... 16 1. Achan Koil Dharma Sastha ...................................................... 23 2. Alathiyur Perumthiri(Hanuman) koil ................................. 24 3. Randu Moorthi temple of Alathur......................................... 27 4. Ambalappuzha Krishnan temple ........................................... 28 5. Amedha Saptha Mathruka Temple ....................................... 31 6. Ananteswar temple of Manjeswar ........................................ 35 7. Anchumana temple , Padivattam, Edapalli....................... 36 8. Aranmula Parthasarathy Temple ......................................... 38 9. Arathil Bhagawathi temple ..................................................... 41 10. Arpuda Narayana temple, Thirukodithaanam ................. 45 11. Aryankavu Dharma Sastha ...................................................... 47 12. Athingal Bhairavi temple ......................................................... 48 13. Attukkal BHagawathy Kshethram, Trivandrum ............. 50 14. Ayilur Akhileswaran (Shiva) and Sri Krishna temples ........................................................................................................... -
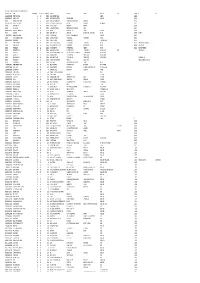
Mgl-Int 1-2012-Unpaid Shareholders List As on 31
MGL-INT 1-2012-UNPAID SHAREHOLDERS AS ON 31-10-2017 DEMAT ID_FOLIO NAME WARRANT NO MICR DIVIDEND AMOUNT ADDRESS 1 ADDRESS 2 ADDRESS 3 ADDRESS 4 CITY PINCODE JH1 JH2 1202140000080651 SHOBHIT AGARWAL 19 29 25000.00 7/150, SWAROOP NAGAR KANPUR 208002 IN30047642921350 VAGMI KUMAR 21 31 32600.00 214 PANCHRATNA COMPLEX OPP BEDLA ROAD UDAIPUR 313001 001431 JITENDRA DATTA MISRA 22 32 12000.00 BHRATI AJAY TENAMENTS 5 VASTRAL RAOD WADODHAV PO AHMEDABAD 382415 IN30163741220512 DURGA PRASAD MEKA 34 44 10183.00 H NO 4 /60 NARAYANARAO PETA NAGARAM PALVONCHA KHAMMAM 507115 001424 BALARAMAN S N 37 47 20000.00 14 ESOOF LUBBAI ST TRIPLICANE MADRAS 600005 001440 RAJI GOPALAN 59 69 20000.00 ANASWARA KUTTIPURAM THIROOR ROAD KUTTYPURAM KERALA 679571 IN30089610488366 RAKESH P UNNIKRISHNAN 72 82 12250.00 KRISHNA AYYANTHOLE P O THRISSUR THRISSUR 680003 002151 REKHA M R 74 84 12000.00 D/O N A MALATHY MAANASAM RAGAMALIKAPURAM,THRISSUR KERALA 680004 THARA P D 1204470005875147 VANAJA MUKUNDAN 161 171 11780.00 1/297A PANAKKAL VALAPAD GRAMA PANCHAYAT THRISSUR 680567 000050 HAJI M.M.ABDUL MAJEED 231 241 20000.00 MUKRIAKATH HOUSE VATANAPALLY TRICHUR DIST. KERALA 680614 IN30189511089195 SURENDRAN 245 255 17000.00 KAKKANATT HOUSE KUNDALYUR P O THRISSUR, KERALA 680616 000455 KARUNAKARAN K.K. 280 290 30000.00 KARAYIL THAKKUTTA HOUSE CHENTRAPPINNI TRICHUR DIST. KERALA 680687 MRS. PAMILA KARUNAKARAN 001233 DR RENGIT ALEX 300 310 20000.00 NALLANIRAPPEL PO KAPPADU KANJIRAPPALLY KOTTAYAM DT KERALA 686508 MINU RENGIT 001468 THOMAS JOHN 309 319 20000.00 THOPPIL PEEDIKAYIL KARTHILAPPALLY ALLEPPEY KERALA 690516 THOMAS VARGHESE 000642 JNANAPRAKASH P.S. -
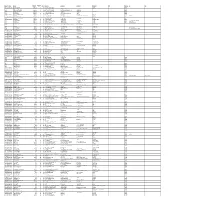
Mgl-Int 1-2012-Unpaid Shareholders List As on 09
DIVIDEND WARRANT DEMAT ID_FOLIO NAME MICR ADDRESS 1 ADDRESS 2 ADDRESS 3 ADDRESS 4 CITY PINCODE JH1 JH2 AMOUNT NO 1202140000080651 SHOBHIT AGARWAL 25000.00 19 29 7/150, SWAROOP NAGAR KANPUR 208002 IN30047642921350 VAGMI KUMAR 32600.00 21 31 214 PANCHRATNA COMPLEX OPP BEDLA ROAD UDAIPUR 313001 001431 JITENDRA DATTA MISRA 12000.00 22 32 BHRATI AJAY TENAMENTS 5 VASTRAL RAOD WADODHAV PO AHMEDABAD 382415 IN30163741220512 DURGA PRASAD MEKA 10183.00 34 44 H NO 4 /60 NARAYANARAO PETA NAGARAM PALVONCHA KHAMMAM 507115 001424 BALARAMAN S N 20000.00 37 47 14 ESOOF LUBBAI ST TRIPLICANE MADRAS 600005 001440 RAJI GOPALAN 20000.00 59 69 ANASWARA KUTTIPURAM THIROOR ROAD KUTTYPURAM KERALA 679571 IN30089610488366 RAKESH P UNNIKRISHNAN 12250.00 72 82 KRISHNA AYYANTHOLE P O THRISSUR THRISSUR 680003 002151 REKHA M R 12000.00 74 84 D/O N A MALATHY MAANASAM RAGAMALIKAPURAM,THRISSUR KERALA 680004 THARA P D 1204470005875147 VANAJA MUKUNDAN 11780.00 161 171 1/297A PANAKKAL VALAPAD GRAMA PANCHAYAT THRISSUR 680567 000050 HAJI M.M.ABDUL MAJEED 20000.00 231 241 MUKRIAKATH HOUSE VATANAPALLY TRICHUR DIST. KERALA 680614 IN30189511089195 SURENDRAN 17000.00 245 255 KAKKANATT HOUSE KUNDALYUR P O THRISSUR, KERALA 680616 000455 KARUNAKARAN K.K. 30000.00 280 290 KARAYIL THAKKUTTA HOUSE CHENTRAPPINNI TRICHUR DIST. KERALA 680687 MRS. PAMILA KARUNAKARAN 001233 DR RENGIT ALEX 20000.00 300 310 NALLANIRAPPEL PO KAPPADU KANJIRAPPALLY KOTTAYAM DT KERALA 686508 MINU RENGIT 001468 THOMAS JOHN 20000.00 309 319 THOPPIL PEEDIKAYIL KARTHILAPPALLY ALLEPPEY KERALA 690516 THOMAS VARGHESE 000642 JNANAPRAKASH P.S. 2000.00 326 336 POZHEKKADAVIL HOUSE P.O.KARAYAVATTAM TRICHUR DIST. -

Ancient Indian Mathematics – a Conspectus*
GENERAL ARTICLE Ancient Indian Mathematics – A Conspectus* S G Dani India has had a long tradition of more than 3000 years of pursuit of Mathematical ideas, starting from the Vedic age. The Sulvasutras (which in- cluded Pythagoras theorem before Pythagoras), the Jain works, the base 10 representation (along with the use of 0), names given to powers of 10 S G Dani is a Distinguished up to 1053, the works of medieval mathematicians Professor at the Tata motivated by astronomical studies, and ¯nally Institute of Fundamental Research, Mumbai. He the contributions of the Kerala school that came obtained his bachelor’s, strikingly close to modern mathematics, repre- master’s and PhD degrees sent the various levels of intellectual attainment. from the University of Mumbai. His areas of There is now increasing awareness around the world that interest are dynamics and as one of the ancient cultures, India has contributed sub- ergodic theory of flows on stantially to the global scienti¯c development in many homogeneous spaces, spheres, and mathematics has been one of the recognized probability measures on Lie groups areas in this respect. The country has witnessed steady and history of mathematics. mathematical developments over most part of the last He has received 3,000 years, throwing up many interesting mathemati- several awards including cal ideas well ahead of their appearance elsewhere in the the Ramanujan Medal and the world, though at times they lagged behind, especially in TWAS Prize. the recent centuries. Here are some episodes from the fascinating story that forms a rich fabric of the sustained * This is a slightly modified ver- intellectual endeavour. -

Extracts of Annual Return 2019
First Name Middle Name Last Name Folio Number DP ID-Client Id Account Number Number of Shares held Class of Shares First Name Middle Name Last Name Folio Number DP ID-Client Id Accoount Number Number of shares held Class of shares A A PALANIAPPAN IN30154914500110 3000 Equity Shares A ABDULMUTHALEEF IN30039418411288 500 Equity Shares A ABDULVAHEETH 1203320009143157 100 Equity Shares A AKILA IN30177413526661 645 Equity Shares A ANBANANTHAN A005295 2100 Equity Shares A ARUNA KUMARI IN30154954641721 250 Equity Shares A ARUNMANI 1208160001178720 350 Equity Shares A ASHOK KUMAR 1203230002287272 998 Equity Shares A ATHIYAN IN30163741910124 200 Equity Shares A BABU 1204010000058132 500 Equity Shares A BALA GANESAN IN30108022126704 710 Equity Shares A BENNETT IN30023911722735 700 Equity Shares A BHAGAVATHIAMMAL 1601430105165465 500 Equity Shares A C MAVANI HUF IN30048429312899 2000 Equity Shares A C THARKAR 1301740000013364 200 Equity Shares A C V SEKHARA RAO IN30267933159089 2 Equity Shares A C VARGHESE IN30151610218693 100 Equity Shares A C VIGNESH IN30039419519831 200 Equity Shares A C VISWANATHAN IN30088813141151 3630 Equity Shares A Carrolene Vincia IN30281410739842 150 Equity Shares A Chanchal Surana 1207650000001416 4050 Equity Shares A DEEPA N KAMATH IN30113526276499 50 Equity Shares A DEEPA RANI IN30051320083659 410 Equity Shares A DEVENDRAN IN30163740588097 10 Equity Shares A DINESHKUMAR A DINESHKUMAR 1208160000802961 25 Equity Shares A EASWARAN IN30051311035375 100 Equity Shares A G SHARES AND SEC LTD IN30100610091238 290 Equity Shares -

Chapter Two Astrological Works in Sanskrit
51 CHAPTER TWO ASTROLOGICAL WORKS IN SANSKRIT Astrology can be defined as the 'philosophy of discovery' which analyzing past impulses and future actions of both individuals and communities in the light of planetary configurations. Astrology explains life's reaction to planetary movements. In Sanskrit it is called hora sastra the science of time-'^rwRH ^5R5fai«fH5iref ^ ^Tm ^ ^ % ^i^J' 11 L.R. Chawdhary documented the use of astrology as "astrology is important to male or female as is the case of psychology, this branch of knowledge deals with the human soul deriving awareness of the mind from the careful examination of the facts of consciousness. Astrology complements everything in psychology because it explains the facts of planetary influences on the conscious and subconscious providing a guideline towards all aspects of life, harmony of mind, body and spirit. This is the real use of astrology^. Dr. ^.V.Raman implies that "astrology in India is a part of the whole of Indian culture and plays an integral part in guiding life for all at all stages of life" ^. Predictive astrology is a part of astronomy that exists by the influence of ganita and astronomical doctrines. Winternitz observes that an astrologer is required to possess all possible noble quantities and a comprehensive knowledge of astronomy, ' Quoted from Sabdakalpadruma, kanta-ll, p.550 ^ L.R.Chawdhari, Secrets of astrology. Sterling Paper backs, New Delhi,1998, p.3 ^Raman.B.V, Planetary influence of Human affairs, U.B.S. Publishers, New Delhi, 1996,p.147 52 mathematics and astrology^ Astrology or predictive astrology is said to be coconnected with 'astronomy'. -

Introduction*
INTRODUCTION | 1 Introduction* Radhavallabh Tripathi IT is almost an impossible task for a single person to present a comprehensive view on the status and trends of Sanskrit studies in a vast country like India. What is being done here would just appear to be a sketchy account, containing snippets of information, that is to be further corroborated, properly analysed and explored. India is divided into 28 states, 7 union territories and 644 districts. There is hardly any district or region where Sanskrit is not studied in some form or the other. Sanskrit is mentioned in the list of 22 major languages, officially accepted in the Constitution of India, and it is also one of the three languages there, that have an all India character. Teaching, Education and Research In India there are 282 universities as per the records with the AIU, at least 112 of which have postgraduate and research departments of Sanskrit. The number of colleges teaching Sanskrit is around 10,000. “Modern methods” are adopted in these institutions for teaching programmes in Sanskrit. Apart from these universities and colleges, there are 16 Sanskrit universities and a number of Sanskrit pÀÇhaœÀlÀs or Sanskrit * This is an enlarged and revised version of my paper “Sanskrit Studies in India” published in the Bulletin of IASS, 2012. 2 | SIXTY YEARS OF SANSKRIT STUDIES: VOL. 1 colleges where traditional method also known as pÀÇhaœÀlÀ paddhati is practised. As per a recent state-wise survey conducted by the Rashtriya Sanskrit Sansthan (RSkS) the number of Sanskrit pÀÇhaœÀlÀs in Madhya Pradesh is 644, in Chhattisgarh 32, in Uttar Pradesh 1347, Uttarakhand 115, in Karnataka it is 290, in Orissa 433, Punjab 8, Rajasthan 1698, Sikkim 36, Tamil Nadu 55, and in Himachal Pradesh 129, Andhra Pradesh 509, Assam 83, Bihar 717, Goa 4, Gujarat 63, Haryana 74, Jammu & Kashmir 43, Jharkhand 3, Kerala 31, Maharashtra 63, Manipur 8. -

Ganita-Yukti-Bhāṣā (Rationales in Mathematical Astronomy) of Jyeṣṣhadeva Volume I: Mathematics Volume II: Astronomy
K.V. Sarma, K. Ramasubramanian, M.D. Srinivas, M.S. Sriram Ganita-Yukti-Bhāṣā (Rationales in Mathematical Astronomy) of Jyeṣṣhadeva Volume I: Mathematics Volume II: Astronomy Series: Sources and Studies in the History of Mathematics and Physical Sciences ▶ A long-awaited translation of one of the most important and hitherto least accessible works in Indian mathematics ▶ Supplemented by detailed explanatory notes and commentary Ganita-yukti-bhasa (Rationales in Mathematical Astronomy) of Jyesthadeva (c.1530) is a seminal text of the Kerala school of astronomy. It is composed in the Malayalam language and presents detailed yuktis or explanations and demonstrations for the results and processes of mathematical astronomy. The text, comprising fifteen chapters, is naturally divided into two parts, mathematics and astronomy, and purports to give an exposition of the techniques and theories employed in the computation of planetary motions as set 2008, LXVIII, 1084 p. In 2 volumes, not forth in the great treatise Tantrasangraha (c.1500) of Nilakantha Somayaji. Even though available separately. the importance of Ganita-yukti-bhasa was brought to the attention of modern scholarship by C.M Whish in the 1830s, a critical edition of the entire Malayalam text is published here for the first time along with an English translation and detailed explanatory notes. Printed book The mathematics part is divided into seven chapters. The topics covered are Parikarma Hardcover (logistics), Dasaprasna (ten problems), Bhinnaganita (fractions), Trairasika (rule of 199,99 € | £179.99 | $249.99 ▶ three), Kuttakara (linear indeterminate equations), Paridhi and Vyasa (infinite series and *213,99 € (D) | 219,99 € (A) | CHF 236.00 ▶ approximations for the ratio of the circumference and diameter of a circle) and Jyanayana (infinite series and approximations for sines). -

History of Science and Technology in India
DDCE/History (M.A)/SLM/Paper HISTORY OF SCIENCE AND TECHNOLOGY IN INDIA By Dr. Binod Bihari Satpathy 1 CONTENT HISTORY OF SCIENCE AND TECHNOLOGY IN INDIA Unit.No. Chapter Name Page No Unit-I. Science and Technology- The Beginning 1. Development in different branches of Science in Ancient India: 03-28 Astronomy, Mathematics, Engineering and Medicine. 2. Developments in metallurgy: Use of Copper, Bronze and Iron in 29-35 Ancient India. 3. Development of Geography: Geography in Ancient Indian Literature. 36-44 Unit-II Developments in Science and Technology in Medieval India 1. Scientific and Technological Developments in Medieval India; 45-52 Influence of the Islamic world and Europe; The role of maktabs, madrasas and karkhanas set up. 2. Developments in the fields of Mathematics, Chemistry, Astronomy 53-67 and Medicine. 3. Innovations in the field of agriculture - new crops introduced new 68-80 techniques of irrigation etc. Unit-III. Developments in Science and Technology in Colonial India 1. Early European Scientists in Colonial India- Surveyors, Botanists, 81-104 Doctors, under the Company‘s Service. 2. Indian Response to new Scientific Knowledge, Science and 105-116 Technology in Modern India: 3. Development of research organizations like CSIR and DRDO; 117-141 Establishment of Atomic Energy Commission; Launching of the space satellites. Unit-IV. Prominent scientist of India since beginning and their achievement 1. Mathematics and Astronomy: Baudhayan, Aryabhtatta, Brahmgupta, 142-158 Bhaskaracharya, Varahamihira, Nagarjuna. 2. Medical Science of Ancient India (Ayurveda & Yoga): Susruta, 159-173 Charak, Yoga & Patanjali. 3. Scientists of Modern India: Srinivas Ramanujan, C.V. Raman, 174-187 Jagdish Chandra Bose, Homi Jehangir Bhabha and Dr. -

Understanding Ancient Indian Mathematics - the Hindu 2/9/14 3:18 PM
Understanding ancient Indian mathematics - The Hindu 2/9/14 3:18 PM S & T » Science Published: December 26, 2011 02:58 IST | Updated: December 26, 2011 03:02 IST ! Understanding ancient Indian mathematics S.G. Dani A portion of a dedication tablet in a rock-cut Vishnu temple in Courtesy: Bill Casselman Gwalior built in 876 AD. The number 270 seen in the inscription features the oldest extant zero in India. It is high time we studied our mathematical heritage with diligence and objectivity Quite often I find that conversations, with people from various walks of life, on ancient Indian mathematics slide to “Vedic mathematics” of the “16 sutras” fame, which is supposed to endow one with magical powers of calculation. Actually, the “16 sutras” were introduced by Bharati Krishna Tirthaji, who was the Sankaracharya of Puri from 1925 until he passed away in 1960, associating with them procedures for certain arithmetical or algebraic computations. Thus, this so-called “Vedic mathematics (VM)” is essentially a 20th century phenomenon. Neither the “sutras” nor the procedures that they are supposed to yield, or correspond to, have anything to do with either the Vedas, or even with any post-Vedic mathematical tradition of yore in India. The image that it may conjure up of ancient rishis engaged in such arithmetical exercises as are taught to the children in the name of VM, and representing the solutions through word-strings of a few words in modern styled Sanskrit, with hardly any sentence structure or grammar, is just too far from the realm of the plausible. -

Medieval State and Society
M.A. HISTORY - II SEMESTER STUDY MATERIAL PAPER – 2.1 MEDIEVAL STATE AND SOCIETY UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION Prepared by: Dr.N.PADMANABHAN Reader, P.G.Department of History C.A.S.College, Madayi Dt.Kannur-Kerala. 2008 Admission MA HIS Pr 2. 1 (M.S & S) 405 UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION STUDY MATERIAL II SEMESTER M.A. HISTORY PAPER - 2. 1 MEDIEVAL STATE AND SOCIETY Prepared by: Dr. N.Padmanabhan Reader P.G.Department of History C.A.S.College, Madayi P.O.Payangadi-RS-670358 Dt.Kannur-Kerala. Type Setting & Layout: Computer Section, SDE. © Reserved 2 CHAPTERS CONTENTS PAGES I TRANSITION FROM ANCIENT TO MEDIEVAL II MEDIEVAL POLITICAL SYSTEM III AGRARIAN SOCIETY 1V MEDIEVAL TRADE V MEDIEVAL SCIENCE AND TECHNOLOGY V1 RELIGION AND IDEOLOGY V11 TRANSITION FROM MEDIEVAL TO MODERN 3 CHAPTER- I TRANSITION FROM ANCIENT TO MEDIEVAL For the sake of the convenience of study history has been divided into three – the ancient, medieval and modern periods.Of course we do not have any date or even a century to demarcate these periods.The concept of ancient, medieval and modern is amorphous.It varies according to regions. Still there are characteristic features of these epochs.The accepted demarcations of ancient, medieval and modern world is a Europo centric one.The fall of Western Roman empire in AD 476 is considered to be the end of ancient period and beginning of the middle ages.The eastern Roman empire continued to exist for about a thousand years more and the fall of the eastern Roman empire in 1453, following the conquest of Constantinople by the Turks is considered to be the end of the medieval period and the beginning of modern period.The general features of the transition from ancient to medieval world the decline of ancient empire decline of trade and urban centres, development of feudal land relations growth of regional kingdoms in the West, emergence of new empires in the Eastern, etc. -

Lal峹fo}Rifjpkf;Dk
laLÑrfo}Rifjpkf;dk Inventory of Sanskrit Scholars laLÑrfo}Rifjpkf;dk INVENTORY OF SANSKRIT SCHOLARS General Editor Radha Vallabh Tripathi RASHTRIYA SANSKRIT SANSTHAN Deemed University New Delhi Board of Advisors Prof. R. Devanathan Prof. Azad Mishra Prof. K. B. Subbarayudu Dr. Sukla Mukherjee Editorial Board Dharmendra Kumar Singhdeo Kailas Chandra Dash Ashok Thapliyal Sangita Gundecha Editorial Assistants Sanjay Dwivedi Sushma Sharma Mangilal Chauhan Surendra Tiwari Nirupama Singhdeo Avani Sharma Vishnu Prasad Meena Data Entry Lala Ram Gohar Sonraj Patidar Amit Kumar Publisher : Registrar RASHTRIYA SANSKRIT SANSTHAN Deemed University 56-57, Institutional Area, Janakpuri, New Delhi – 110 058 First Edition 2012 © Publisher Price 450.00 ISBN -978-93-86111-85-2 Printed at : New Bharatiya Book Corporation, New Delhi PREFACE It is immensely gratifying that the Rashtriya Sanskrit Sansthan, New Delhi is publishing the ‘Inventory of Sanskrit Scholars’ (laaLÑrfo}Rifjpkf;dk) on the occasion of Fifteenth World Sanskrit Conference. The Sansthan under its various schemes also intends to collect the Bio-data of Sanskrit Scholars and to make them available on its website. The preparation of the Software for this purpose is in its final stage. The website will give an access to know the Sanskrit scholars of the entire world and the works done by them. The present Inventory includes the details of about 5000 Sanskrit scholars. Initially, the preparation of Inventory was taken up at the Bhopal Campus of the Sansthan. Since 2009 the Bhopal Campus has been doing this work in collaboration with its Main Campus, The Rashtriya Sanskrit Sansthan, New Delhi. This Inventory on the basis of details made available by scholars in response to the Sansthan’s format presents briefly the data as under - the name of scholars, qualification, date of birth, place of birth, positions, teachers and disciples (Guru- Shishya-Parampara), numbers and titles of published books and research papers, addresses, awards and honors, foreign visits etc.