Power Screws
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Screw Thread Systems
Machinery's Handbook 27th Edition TABLE OF CONTENTS THREADS AND THREADING SCREW THREAD SYSTEMS METRIC SCREW THREADS 1725 Screw Thread Forms 1783 American Standard Metric Screw 1725 V-Thread, Sharp V-thread Threads M Profile 1725 US Standard Screw Thread 1783 Comparison with Inch Threads 1725 Unified Screw Thread Forms 1783 Interchangeability 1726 International Metric Thread 1783 Definitions 1727 Definitions of Screw Threads 1784 Basic M Profile 1784 M Crest and Root Form UNIFIED SCREW THREADS 1785 General Symbols 1732 American Standard for Unified 1785 M Profile Screw Thread Series Screw Threads 1785 Mechanical Fastener Coarse Pitch 1732 Revised Standard 1786 M Profile Data 1732 Advantages of Unified Threads 1787 Limits and Fits 1732 Thread Form 1793 Dimensional Effect of Coating 1733 Internal and External Screw 1793 Formulas for M Profile Thread Design Profile 1797 Tolerance Grade Comparisons 1733 Thread Series 1797 M Profile Limiting Dimension 1734 Inch Screw Thread 1798 Internal Metric Thread 1735 Diameter-Pitch Combination 1800 External Metric Thread 1736 Standard Series Combinations 1804 American Standard Metric Screw 1763 Coarse-Thread Series Threads MJ Profile 1764 Fine-Thread Series 1804 Diameter-Pitch Combinations 1764 Extra-Fine-Thread Series 1807 Trapezoidal Metric Thread 1765 Constant Pitch Series 1807 Comparison of ISO and DIN 1766 4-Thread Series Standards 1767 6-Thread Series 1813 Trapezoidal Metric Thread 1768 8-Thread Series 1814 ISO Miniature Screw Threads 1769 12-Thread Series 1814 British Standard ISO Metric Screw 1770 16-Thread Series Threads 1771 20-Thread Series 1814 Basic Profile Dimensions 1772 28-Thread Series 1815 Tolerance System 1773 Thread Classes 1815 Fundamental Deviations 1773 Coated 60-deg. -

Thread Systems
PRECISION GAGE SOLUTIONS 390 Oser Avenue, Hauppauge, New York, U.S.A. 11788 Tel: (800) 767-7633 (631) 231-1515 Fax: (800) 767-2034 (631) 231-1625 Email: [email protected] Web: www.threadcheck.com Thread Systems A thread system is a set of various thread designations which represent different thread sizes to define the thread geometry for example: Thread Series Designations Metric M Unified UNC, UNF, UNS, UN, UNR National Taper Pipe NPT Aeronautical Taper Pipe ANPT British Standard Whitworth BSW ***Please see page 53 of our catalog or please visit our website at www.threadcheck.com under the technical documents and click onto the Basic Screw Thread Designations.*** There are only two major screw thread systems that are used today: 1. The ISO Metric Screw Thread System 2. The Unified Screw Thread System In countries other than the United States and Canada, the ISO Metric Screw Thread System is primarily used today. Unlike, most other countries the United States and Canada still use the Unified (Inch) Thread System. However, both are moving over to the ISO Metric System. It is estimated that approximately 60% of screw threads in use in the United States are still inch based. Other thread designations such as BSW, BSF, BA, etc. are also still in use today but are mostly produced in the capacity of a replacement part. Threads are manufactured by cold forming, cold rolling, hot forming, cold rolling or by the cut-thread process. The most common manufacturing method for standard fasteners up to 1” or 25mm is the cold forming or cold rolling process whereby both the head and the thread are produced with the material in the cold state. -

Manufacturing Processes
Module 7 Screw threads and Gear Manufacturing Methods Version 2 ME, IIT Kharagpur Lesson 31 Production of screw threads by Machining, Rolling and Grinding Version 2 ME, IIT Kharagpur Instructional objectives At the end of this lesson, the students will be able to; (i) Identify the general applications of various objects having screw threads (ii) Classify the different types of screw threads (iii) State the possible methods of producing screw threads and their characteristics. (iv) Visualise and describe various methods of producing screw threads by; (a) Machining (b) Rolling (c) Grinding (i) General Applications Of Screw Threads The general applications of various objects having screw threads are : • fastening : screws, nut-bolts and studs having screw threads are used for temporarily fixing one part on to another part • joining : e.g., co-axial joining of rods, tubes etc. by external and internal screw threads at their ends or separate adapters • clamping : strongly holding an object by a threaded rod, e.g., in c-clamps, vices, tailstock on lathe bed etc. • controlled linear movement : e.g., travel of slides (tailstock barrel, compound slide, cross slide etc.) and work tables in milling machine, shaping machine, cnc machine tools and so on. • transmission of motion and power : e.g., lead screws of machine tools • converting rotary motion to translation : rotation of the screw causing linear travel of the nut, which have wide use in machine tool kinematic systems • position control in instruments : e.g., screws enabling precision movement of the work table in microscopes etc. • precision measurement of length : e.g., the threaded spindle of micrometers and so on. -

Thread Cutting; Working of Screws, Bolt Heads, Or Nuts
B23G THREAD CUTTING; WORKING OF SCREWS, BOLT HEADS, OR NUTS, IN CONJUNCTION THEREWITH (making helical grooves by turning B23B5/48, by milling B23C3/32, by forging, pressing, or hammering B21K1/56, by grinding B24B19/02; arrangements for copying or controlling B23Q; thread forming by corrugating tubes B21D15/04, by rolling B21H3/02) Definition statement This subclass/group covers: Thread cutting by chip removal. Production of threads with no removal of chips by means of tools similar in form and manner of use to thread cutting tools. Working of screws, bolt heads and nuts in conjunction with thread cutting. References relevant to classification in this subclass This subclass/group does not cover: Thread forming by corrugating tubes B21D 15/04 Making threaded elements by B21K 1/26 forging/hammering Making nuts by forging or hammering B21K 1/64 Making screwthreads by rolling B21H 3/00 Turning helical grooves B23B 5/48 Turning tools for threading B23B 27/065 Milling helical grooves B23C 3/32 Making gears (inc wormwheels) B23F Making milling cutters for threading B23P 15/36 Making threading tools B23P 15/48 Multi stage processes involving B23P 23/00 threading and also other operations classed in B23B, B23C, B23D, B23F, making particular items 1 Details of machine tools and B23Q accessories not related to the operation being performed including: - evacuation of swarf, B23Q 11/0042 - guarding & protective coverings B23Q 11/08 - conveying workpiece into and from B23Q 7/00 machine - tool changing B23Q 3/155 - measuring or sensing B23Q 17/00 Adaptive control and/or computer B23Q 15/00, G05B 15/02 controls for turning, boring or drilling processes Grinding helicoidal grooves B24B 19/022 Fasteners per se F16B Special rules of classification within this subclass Classification in this subclass is according to a literal interpretation of the group and subgroup headings. -

JIS (Japanese Industrial Standard) Screw Thread Specifications
JIS (Japanese Industrial Standard) Screw Thread Specifications Note: Although these specifications are based TECHNICAL DATA on JIS they also apply to ISO and DIN threads. Some comments added by Maryland Metrics Courtesy of: copyright 2002 maryland metrics/osg corporation Screw Thread - 1 <Exterior features of thread ridge> (1) Flank : Thread face (excluding crest Figure 1 Basic designation of thread (1) and root of thread profile) Pitch P (2) Crest : The tap surface joining the (Internal (External Internal thread thread) thread) Root two sides or flanks of a Crest Crest clearance thread Angle of thread 1 (3) Root : The bottom surface joining e of Half angl angle alf ad thre of the flanks of two adjacent H thre ad flanks Root radius Height of fundamental external thread Thread overlap H (4) Angle of thread : Angle between adjacent External thread triangle H Major diameter of 1 1 Root clearance 1 D flanks measured at the · cross section of screw (Internal thread)Crest External root thread - including the axis of internal thread D Internal thread D external thread d Minor diameter of Minor diameter of d Major diameter of the screw thread Pitch diameter d2 (5) Flank angle : The angle between the Figure 2 Basic designation of thread (2) individual flank and the perpendicular to the axis of Internal thread Crest the thread measured in the Thread ridge axial plane Angle of thread (6) Pitch : The distance from a point on one thread to a corresponding point on the next thread measured Pitch diameter Pitch diameter parallel to the axis thread External -

Machinists-Handbook-Gcodetutor.Pdf
GCodeTutor.com Machinists Handbook GCodeTutor.com Content Conversion • G74 Peck Drilling • Calculations • G75 Peck Grooving • 1/64” to 1” • G76 Screw Cutting Single Line • 1 1/64” to 2” • G76 Screw Cutting Double Line • 2 1/64” to 3” • G83 Z-axis Peck Drilling Screw Thread Charts • G84 Z-axis Tapping • Metric Coarse Thread • G87 X-axis Peck Drilling • Metric Fine Thread • G88 X-axis Tapping • BSW British Standard Whitworth Thread G Code Canned Cycles - Milling • BSF British Standard Fine Thread • G81 Drilling • BA British Association Screw Thread • G82 Counter bore • BSPP British Standard Pipe parallel • G83 Peck Drilling • BSPT British Standard pipe Taper • G84 Tapping • UNC Unified Coarse Thread • G85 Bore in / Bore out • UNF Unified Fine Thread • G86 Bore in / Rapid out • UNEF Unified Extra Fine Thread Calculations • Reamer Drill Size • Speeds and Feeds Abbreviations • Tapping Drill CNC Programming Reference • Trigonometry • G Code Trigonometry Charts • M Code Tool Geometry • Auxiliary Commands • RH Knife Tool G Code Canned Cycles - Turning • Drill • G70 Finishing • Centre Drill • G71 Roughing • End Mill • G72 Facing • Morse Taper • G73 Pattern Repeating Afterword Machinists Handbook GCodeTutor.com Conversion Charts Machinists Handbook GCodeTutor.com Conversion Calculations Length Kilometers (km) x 0.62 = Miles (mi) Miles (mi) x 1.61 = Kilometers (km) Kilometers (km) x 3280.8 = Feet (ft) Feet (ft) x 0.0003048 = Kilometers (km) Meters (m) x 3.28 = Feet (ft) Feet (ft) x 0.3 = Meters (m) Centimeters (cm) x 0.39 = Inches (in) Inches (in) -

Kid Spark Screws Lesson Plan
Screw v2.1v2.3 Applications in Design & Engineering: Simple Machines Teacher Lesson Plan Introduction Activity Time: 150 Minutes This Kid Spark lesson is designed to introduce students to one of the six simple machines: the screw. Students will become familiar with Target Grade Level: 6-8 how a screw works by learning key information, building and modifying a screw, and then designing and engineering a custom screw to solve a challenge. Educational Standards Click here to explore the entire Kid Spark Curriculum Library. NGSS NGSS Learning Dimensions 3-5-ETS1-4 Engineering Design This Kid Spark lesson engages students in the following learning MS-ETS1-4 Engineering Design dimensions of the Next Generation Science Standards: Scientific/Engineering Practice: ITEEA Planning and carrying out investigations STL8- Attributes of Design STL9- Engineering Design Crosscutting Concept: Cause and effect: Mechanism and explanation STL10- Invention and Innovation STL11- Apply Design Process Learning Objectives STEM Concepts Covered Understand the basic elements and purpose of a screw. Force Mechanical Advantage Calculate the amount of mechanical advantage in a screw. Effort Prototyping Load Critical Thinking Modify a screw to increase mechanical advantage. Work Multiplication Design and engineer a custom screw to solve a challenge. Motion Division Distance Units of Measurement Simple Machines Pitch Learning Steps This lesson will use the following steps to help students learn about the screw. 2. Build 3. Design 1. Learn & Modify & Engineer Elements -

A Small Desktop CNC Lathe Can Be Used to Create Precise Threads
Single Point Threading on a Desktop CNC Lathe. A small desktop CNC lathe can be used to create precise threads. The threads can be any of the standard US unified series, or the common metric threads. In addition, nearly any combination of screw diameter and thread pitch can be quickly programmed and successfully cut. Machinery’s Handbook is an excellent source for all the details of thread design dimensions. For all modern V cross-section screws, a tool with a 60-degree ground tip is required. This tool is mounted and aligned within a ½ degree or so, with a turned diameter in the lathe chuck, using a threading gage, such as Starrett part No. C391 to align the threading tool. The goal for the expert thread turner is to mount and set his tool, then run a perfect first part. Few are able to accomplish this due to that fact that a thread is measured at the thread pitch, rather than the minor diameter. The tool tip cuts at the minor diameter, and so the process is always one of cut, measure, adjust, re-cut, re-measure, re-cut, etc, until the thread is finally the right size. Not all low cost CNC controllers permit re-cutting a thread. DeskCNC is one that does. The tools used to measure the thread pitch are either a thread micrometer, which is relatively expensive, or the 3-wire method, which uses a standard micrometer and 3 steel wires to measure the pitch diameter. Thread wire sets are very inexpensive and include full instructions on how to measure a thread pitch. -
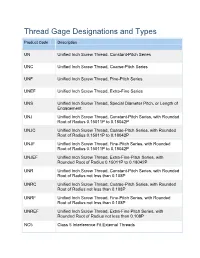
Thread Gage Designations and Types
Thread Gage Designations and Types Product Code Description UN Unified Inch Screw Thread, Constant-Pitch Series UNC Unified Inch Screw Thread, Coarse-Pitch Series UNF Unified Inch Screw Thread, Pine-Pitch Series UNEF Unified Inch Screw Thread, Extra-Fine Series UNS Unified Inch Screw Thread, Special Diameter Pitch, or Length of Engagement UNJ Unified Inch Screw Thread, Constant-Pitch Series, with Rounded Root of Radius 0.15011P to 0.18042P UNJC Unified Inch Screw Thread, Coarse-Pitch Series, with Rounded Root of Radius 0.15011P to 0.18042P UNJF Unified Inch Screw Thread, Fine-Pitch Series, with Rounded Root of Radius 0.15011P to 0.18042P UNJEF Unified Inch Screw Thread, Extra-Fine-Pitch Series, with Rounded Root of Radius 0.15011P to 0.18042P UNR Unified Inch Screw Thread, Constant-Pitch Series, with Rounded Root of Radius not less than 0.108P UNRC Unified Inch Screw Thread, Coarse-Pitch Series, with Rounded Root of Radius not less than 0.108P UNRF Unified Inch Screw Thread, Fine-Pitch Series, with Rounded Root of Radius not less than 0.108P UNREF Unified Inch Screw Thread, Extra-Fine Pitch Series, with Rounded Root of Radius not less than 0.108P NC5 Class 5 Interference Fit External Threads Product Code Description NC5HF For Driving in Hard Ferrous Material of Hardness over 160 Bhn NC5CSF For Driving Copper Alloy and Soft Ferrous Material of 160 Bhn or less NC5ONF For Driving in Other NonFerrous Material (Nonferrous Materials Other Than Copper Alloys, Any Hardness) NC5 Class 5 Interference Fit Internal Threads NC5IF Entire Ferrous Material -

QP158 Thread Inspection Procedure Owner: Quality Manager Change History: See DCN for Details Rev Date DCN Number Current Revision E 2018‐0201 DCN15947
Quality Procedure QP158 Thread Inspection Procedure Owner: Quality Manager Change History: See DCN for Details Rev Date DCN Number Current Revision E 2018‐0201 DCN15947 1. PURPOSE 1.1. This procedure defines the control method for thread inspection to ensure that product meets design requirements. 2. SCOPE 2.1. This procedure applies to manufactured and procured components and tooling with internal or external threads. 3. DEFINITIONS 3.1. Thread ‐ A helical structure used to convert between rotational and linear movement or force. A screw thread is a ridge wrapped as a helix around either a cylinder (a straight thread) or a cone (a tapered thread). Threads can be used as a simple machine or as a fastener. Threads can be left or right‐handed and internal or external. Thread form is the cross‐sectional form of a thread. Inch threads are typically documented by stating the diameter of the thread followed by the threads per inch, such as 3/8‐18 which is a 3/8 inch diameter thread with 18 threads per inch, or by thread angle, which is the angle between the threads. This angle determines the style or type of thread (i.e. NPT, pipe thread). Metric threads are defined by their pitch. Example: M16 x 1.25 x 30 has a pitch of 1.25 and a 16mm major diameter and a length of 30mm. 3.2. Lead Angle ‐ On the straight thread, it is the angle made by the helix of the thread at the pitch line with a plane perpendicular to the axis. Lead angle is measured in an axial plane. -
Acme Thread Pitch Chart Pdf
Acme thread pitch chart pdf Continue About Us Contact Us Disclaimer ? Privacy PolicyCopyright © 2013-2020 About Us Contact Us Disclaimer ? Privacy PolicyCopyright © 2013-2020 Screw thread profiles with trapezoidal contours This article includes a list of general references, but remains largely unverified because it lacks enough corresponding online appointments. Please help to improve this article by introducing more accurate quotes. (April 2015) (Learn how and when to delete this template message) Metric trapezoidal thread, TR-40×7. Male Acme thread trapezoidal thread shapes are screw thread profiles with trapezoidal contours. They are the most common forms used for lead screws (power screws). They offer high strength and ease of manufacture. They are usually located where large loads are required, such as in a visor or the lead screw of a lathe. [1] Standardized variations include multi-start threads, left threads, and self-centering wires (which are less likely to join under lateral forces). The original shape of the trapezoidal thread, and probably the most commonly found worldwide, with a thread angle of 29o, is the acme thread shape (/-kmi/ AK-me). The Acme thread was developed in 1894 as a very suitable profile for power screws that has several advantages over the square thread,[note 1] which had been the way of choice until then. It is easier to cut with single-point threading or die than the square thread is (because the shape of the thread requires a tool bit or die-tooth geometry that is not suitable for cutting). It is used better than a square thread (because wear can be compensated) and is stronger than a square thread of comparable size. -

Screw Thread Micrometer with Interchangeable Tips
Screw Thread Micrometer with Interchangeable Tips Series 126 Specifications Accuracy Refer to the list of specifications This Screw Thread Micrometer comes with optional, interchangeable, anvils/spindle-tips that allow Graduation 0,01 mm you to measure a wide range of metric/unified and Whitworth screw-thread pitch diameters. Scale Thimble and sleeve satin chrome finish, ø18 mm Measuring With spindle lock, ø 6,35 mm, spindle spindle pitch 0,5 mm Measuring 5-10 N force Delivered Including box, setting standard (60°) (from 25 mm upward), key Interchangeable anvils/spindle tips not included Interchangeable anvils/spindle tips Standard accessories 126-125 in matching pairs No. Description 167-261 Setting standard 25 mm/60° Metric 167-262 Setting standard 50 mm/60° Range Accuracy L a Mass No. 167-263 Setting standard 75 mm/60° [mm] [µm] [mm] [mm] [g] 167-264 Setting standard 100 mm/60° 126-125 0-25 ±4 39,5 25 240 167-265 Setting standard 125 mm/60° 126-126 25-50 ±4 64,5 32 290 167-266 Setting standard 150 mm/60° 126-127 50-75 ±4 90 45 390 167-267 Setting standard 175 mm/60° 126-128 75-100 ±5 115,6 65 450 167-268 Setting standard 200 mm/60° 126-129 100-125 ±5 140,6 79 530 167-269 Setting standard 225 mm/60° 126-130 125-150 ±5 165,6 93 620 167-270 Setting standard 250 mm/60° 126-131 150-175 ±6 190,5 105 730 167-271 Setting standard 275 mm/60° 126-132 175-200 ±6 214,5 120 860 126-133 200-225 ±6 240,5 131 1030 Optional accessories 126-134 225-250 ±7 265,5 144 1200 No.