Finding the Land of Opportunity Intergenerational Mobility in Denmark
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Connecting Øresund Kattegat Skagerrak Cooperation Projects in Interreg IV A
ConneCting Øresund Kattegat SkagerraK Cooperation projeCts in interreg iV a 1 CONTeNT INTRODUCTION 3 PROgRamme aRea 4 PROgRamme PRIORITIes 5 NUmbeR Of PROjeCTs aPPROveD 6 PROjeCT aReas 6 fINaNCIal OveRvIew 7 maRITIme IssUes 8 HealTH CaRe IssUes 10 INfRasTRUCTURe, TRaNsPORT aND PlaNNINg 12 bUsINess DevelOPmeNT aND eNTRePReNeURsHIP 14 TOURIsm aND bRaNDINg 16 safeTy IssUes 18 skIlls aND labOUR maRkeT 20 PROjeCT lIsT 22 CONTaCT INfORmaTION 34 2 INTRODUCTION a short story about the programme With this brochure we want to give you some highlights We have furthermore gathered a list of all our 59 approved from the Interreg IV A Oresund–Kattegat–Skagerrak pro- full-scale projects to date. From this list you can see that gramme, a programme involving Sweden, Denmark and the projects cover a variety of topics, involve many actors Norway. The aim with this programme is to encourage and and plan to develop a range of solutions and models to ben- support cross-border co-operation in the southwestern efit the Oresund–Kattegat–Skagerrak area. part of Scandinavia. The programme area shares many of The brochure is developed by the joint technical secre- the same problems and challenges. By working together tariat. The brochure covers a period from March 2008 to and exchanging knowledge and experiences a sustainable June 2010. and balanced future will be secured for the whole region. It is our hope that the brochure shows the diversity in Funding from the European Regional Development Fund the project portfolio as well as the possibilities of cross- is one of the important means to enhance this development border cooperation within the framework of an EU-pro- and to encourage partners to work across the border. -

CEMENT for BUILDING with AMBITION Aalborg Portland A/S Portland Aalborg Cover Photo: the Great Belt Bridge, Denmark
CEMENT FOR BUILDING WITH AMBITION Aalborg Portland A/S Cover photo: The Great Belt Bridge, Denmark. AALBORG Aalborg Portland Holding is owned by the Cementir Group, an inter- national supplier of cement and concrete. The Cementir Group’s PORTLAND head office is placed in Rome and the Group is listed on the Italian ONE OF THE LARGEST Stock Exchange in Milan. CEMENT PRODUCERS IN Cementir's global organization is THE NORDIC REGION divided into geographical regions, and Aalborg Portland A/S is included in the Nordic & Baltic region covering Aalborg Portland A/S has been a central pillar of the Northern Europe. business community in Denmark – and particularly North Jutland – for more than 125 years, with www.cementirholding.it major importance for employment, exports and development of industrial knowhow. Aalborg Portland is one of the largest producers of grey cement in the Nordic region and the world’s leading manufacturer of white cement. The company is at the forefront of energy-efficient production of high-quality cement at the plant in Aalborg. In addition to the factory in Aalborg, Aalborg Portland includes five sales subsidiaries in Iceland, Poland, France, Belgium and Russia. Aalborg Portland is part of Aalborg Portland Holding, which is the parent company of a number of cement and concrete companies in i.a. the Nordic countries, Belgium, USA, Turkey, Egypt, Malaysia and China. Additionally, the Group has acti vities within extraction and sales of aggregates (granite and gravel) and recycling of waste products. Read more on www.aalborgportlandholding.com, www.aalborgportland.dk and www.aalborgwhite.com. Data in this brochure is based on figures from 2017, unless otherwise stated. -

New Hospital Construction - Future Hospitals in Denmark
INNOVATING BETTER LIFE SUSTAINABLE HOSPITALS New Hospital Construction - Future Hospitals in Denmark WHITE PAPER SUSTAINABLE HOSPITALS Future Hospitals in Denmark About this white paper Steering Committee This white paper presents the Danish approach to new hospital Danish Ministry of Health, Martin Nyrop Holgersen, [email protected] construction and includes a wide range of innovative solutions that Danish Regions, Kristian Taageby Nielsen, [email protected] contribute to creating sustainable healthcare for the future. It is part North Denmark Region, Niels Uhrenfeldt, [email protected] of a series of white papers that show how Danish solutions can con- Region Zealand, Helle Gaub, [email protected] tribute to increase efficiency in healthcare while empowering patients Region of Southern Denmark, Torben Kyed Larsen, [email protected] and staff. Danish Export Association, Thomas Andersen, [email protected] Danish healthcare innovation is not exclusive for the Danes: many Systematic, Jacob Gade, [email protected] years of global presence show that our healthcare products and solu- tions create value internationally. Danish ideas and products are used Contributors every day in hospitals, medical clinics, ambulances, and nursing homes 3XN, Stig Vesterager Gothelf, [email protected] across the world. Agitek, Jean-Paul Bergmann, [email protected] Arkitema Architects, Birgitte Gade Ernst, [email protected] We hope to inspire you and would like to invite you to Denmark to Bim Equity, Ida Maria Sandgreen, [email protected] learn more about the Danish -

Aalborg - Denmark - Europan12 REDEFINING URBAN QUALITY
Aalborg - Denmark - europan12 REDEFINING URBAN QUALITY Aerial photo with strategic elements CATEGORY urban HOW THE SITE CAN CONTRIBUTE TO THE ADAPTABLE CITY? CITY STRATEGY TEAM REPRESENTATIVE architect / urban planner / landscaper Vestbyen is one of the oldest boroughs in Aalborg, established as a residential With a population of 122,000, Aalborg is the largest town in the northernmost area to house the workers employed by industrial advances between 1900 region of Denmark. In recent years, the city has undergone an extreme trans- LOCATION AALBORG and 1950. The district has not developed noticeably since it was built. This is in formation from industrial town to knowledge and experience city. The city has POPULATION City 120 000 inhab. Conurbation 125 000 inhab. contrast to the rest of the city - especially the centre - which has experienced revamped itself as «the city on the fjord», and has over the past 10-15 years STRATEGIC SITE 80 ha SITE OF PROJECT 32 ha major change and expansion over the last few years, with investment in large- made great investments in the regeneration of the central waterfronts and the SITE PROPOSED BY Municipality, Region and housing associations scale international projects. Along with the neighborhood’s untapped poten- central Midtbyen district, which has provided the entire city centre with a lift OWNER OF THE SITE Municipality, Region and housing associations tial, new strategies for Vestbyen can contribute to this development of Aalborg and a new identity. In 1974, a large university was built in the eastern part of as the small but internationally-oriented city. A new strategy for Vestbyen could Aalborg, which today is hugely influential on the city’s growth and business life. -

Educational Strategy 2015 25 09
Educational Strategy 2015-2018 Content Preface 4 Status 6 Vision and goals Sub-goals 1. Broad cooperation among educational institutions 10 Status Goals 2. Innovative cooperation among study programmes and business 12 Status Goals 3. STAY – work after completion of studies 14 Status Goals 4. Development of study environment and housing offers – including CAMPUS 16 Status Goals 5. Cultural and leisure offers with focus on students 18 Status Goals 6. Globalisation and internationalisation 20 Status Goals Marketing the educational city 22 Appendices 24 Preface Aalborg has undergone rapid growth in recent Our goal is for Aalborg to be the town where it years. In 2014, the nearly 41,000 students in Aal- is easiest to get a student job and internship, to borg accounted for approximately 20% of resi- cooperate with the business community etc. – dents in the city. Aalborg can therefore rightly be In Aalborg, you can use what you learn. Aalborg referred to as an educational city. wants to be Denmark’s best educational city. During the period from 2012-2014, many stu- We have already come far… dents chose Aalborg as their educational city. It is our goal to continue to attract students from the Aalborg wants to go even further. We want to Northern Jutland region, but also from the rest commit ourselves. We must actively contribute of the country. A high number of students in Aal- to the creation of alliances between the educa- borg, however, is not a goal in itself. tion and business communities that ensure that students receive a good education, but also a We want students to choose Aalborg because connection to the job market during their studies Aalborg can offer them the education of their and thus far greater chances of getting a job upon dreams, but also because Aalborg Municipality is graduating. -
Participants List
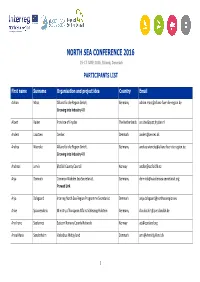
NORTH SEA CONFERENCE 2016 15-17 JUNE 2016, Billund, Denmark PARTICIPANTS LIST First name Surname Organisation and project idea Country Email Adrian Mass Allianz für die Region GmbH, Germany [email protected] Growing into Industry 4.0 Albert Ruiter Province of Fryslan The Netherlands a.ruiter"fryslan.nl Anders Laustsen CenSec Denmark [email protected] Andrea Wiencke Allianz für die Region GmbH, Germany [email protected] Growing into Industry 4.0 Andreas Lervik Østfold County Council Norway [email protected] Anja Domnick Common Wadden Sea Secretariat, Germany [email protected] Prowad Link Anja Dalsgaard Interreg North Sea Region Programme Secretariat Denmark [email protected] Anke Spoorendonk Ministry of European Affairs Schleswig-Holstein Germany [email protected] Ann Irene Saeternes Eastern Norway County Network Norway [email protected] Anna Maria Sønderholm Væksthus Midtjylland Denmark [email protected] 1 First name Surname Organisation and project idea Country Email Anne Udd Region Halland Sweden [email protected] Ann-Sofie Pauwelyn Waterwegen & Zeekanaal NV Flanders [email protected] Arjen Rodenburg PNO Consultants, CONBIKE and IoTLogistics The Netherlands [email protected] Axel Kristiansen Interreg North Sea Region Programme Secretariat Denmark [email protected] Beate Marie Johnsen Vest-Agder fylkesting Norway [email protected] Benjamin Daumiller Europäisches Institut für Innovation e. V. -

Denmark - on Your Bike! the National Bicycle Strategy
Denmark - on your bike! The national bicycle strategy July 2014 Ministry of Transport Frederiksholms Kanal 27 1220 Copenhagen K Denmark Telefon +45 41 71 27 00 ISBN 978-87-91511-93-6 [email protected] www.trm.dk Denmark - on your bike! The national bicycle strategy 4.| Denmark - on your bike! Denmark - on your bike! Published by: Ministry of Transport Frederiksholms Kanal 27F 1220 Copenhagen K Prepared by: Ministry of Transport ISBN internet version: 978-87-91511-93-6 Frontpage image: Danish Road Directorate Niclas Jessen, Panorama Ulrik Jantzen FOREWORD | 5v Foreword Denmark has a long tradition for cycling and that makes us somewhat unique in the world. We must retain our strong cycling culture and pass it on to our children so they can get the same pleasure of moving through traf- fic on a bicycle. Unfortunately, we cycle less today than we did previously. It is quite normal for Danes to get behind the wheel of the car, even for short trips. It is com- fortable and convenient in our busy daily lives. If we are to succeed in en- couraging more people to use their bicycles, therefore, we must make it more attractive and thus easier to cycle to work, school and on leisure trips. We can achieve this by, for example, creating better cycle paths, fewer stops, secure bicycle parking spaces and new cycling facilities. In the government, we are working for a green transition and we want to promote cycling, because cycling is an inexpensive, healthy and clean form of transport. The state has never before done as much in this regard as we are doing at present. -

Local Acceptance and Communication As Crucial Elements for Realizing CCS in the Nordic Region
Available online at www.sciencedirect.com ScienceDirect Energy Procedia 86 ( 2016 ) 315 – 323 The 8th Trondheim Conference on CO2 Capture, Transport and Storage Local acceptance and communication as crucial elements for realizing CCS in the Nordic region a* b Jacob Kielland Haug , Peter Stigson aSINTEF Energy Research, P.O. Box 4761 Sluppen, NO-7465 Trondheim, Norway bIVL Swedish Environmental Research Institute, Valhallavägen 81, SE-114 27 Stockholm, Sweden Abstract The purpose of this paper was to assess the Nordic situation with regard to carbon capture and storage (CCS) deployment at the local level. This was done by identifying important factors found in the literature on community acceptance and communication and relating this to possible CCS deployment in the Skagerrak region. The analysis was complemented with findings from interviews made with municipalities in the three countries (Denmark, Sweden and Norway). The results show that the possibilities to store CO2 offshore may be a clear advantage for the Nordic region and that Porsgrunn municipality in Norway display very positive attitudes towards existing and potential CCS activities, which stands in contrast to the many public acceptance challenges experienced in Europe. Moreover, the municipalities display very different awareness about CCS, which is seen in relation to CCS experiences and national policies. © 20162015 The Authors. Published by ElsevierElsevier LtdLtd.. This is an open access article under the CC BY-NC-ND license (Peerhttp://creativecommons.org/licenses/by-nc-nd/4.0/-review under responsibility of the Programme Chair). of The 8th Trondheim Conference on CO2 Capture, Transport and Storage. Peer-review under responsibility of the Programme Chair of the 8th Trondheim Conference on CO2 Capture, Transport and Storage Keywords: Local acceptance; communication; Nordic region; Skagerrak 1. -

Medcom8 > How Things Turned
MedCom8 > How things turned out MedCom steering committee Preface 3 MedCom8 – Dissemination and technological future-proofing 4 From MedCom8 to MedCom9 – Effective digitisation 5 Svend Særkjær Head of Department Ministry of Health MedCom’s basic remit 6 Tommy Kjelsgaard Office Manager The Danish Regions MedCom8 project monitoring – How things turned out 7 Christian Harsløf Head of Health Policy Local Government Denmark Project line 1 · Chronic Patient project Flemming Christiansen Sector Manager National eHealth 1.1 Common Chronic Patient Data 8 Peter Simonsen Head of Department Region of Southern Denmark 1.2 Clinically Integrated Home Monitoring 9 Pia Kopke Deputy Director The Capital Region of Denmark Project line 2 · E-records and P-records Mogens Engsig-Karup Chief Strategist Central Denmark Region 2.1 E-records and P-records 10 Jens Parker General Practitioner Danish Medical Association Morten Elbæk Petersen Director Sundhed.dk Project line 3 · Municipal projects Henrik Bruun Head of IT Development Association of Danish Pharmacies 3.1 Home nursing – hospital service 11 3.2 Rehabilitation plan 12 Henrik Bjerregaard Jensen Director MedCom 3.3 Doctor forms (LÆ forms) 13 3.4 Birth registration 14 Project line 4 · Shared Medication Record (FMK) at the general practitioner’s surgery 4.1 Shared Medication Record (FMK) and Danish Vaccination Register (DDV) in the primary sector 15 Project line 5 · Telemedicine 5.1 Video interpreting 16 5.2 Telepsychiatry 17 5.3 Telemedical ulcer assessment 18 5.4 Telemedical mapping 19 Project line 6 · General practitioner and laboratory projects 6.1 Package Referrals and REFPARC 20 6.2 Laboratory medicine 21 Published by MedCom, february 2014 Project line 7 · International projects Text: MedCom 7.1 International projects 22 Editing and graphic design: Project line 8 · Operation and technology Idé Bureauet Reklame & Kommunikation Photos: Colourbox (pp. -

The Role of Pedestrian Safety in the Municipal Trac Safety Planning
© Aleks Magnusson The Role of Pedestrian Safety in the Municipal Traffic Safety Planning When Maintenance Becomes Safety Camilla Lønne Nielsen & Sara Merete Kjeldbjerg Jensen Mobilities and Urban Studies, 2021 Master Thesis R E P O T R T E N D U T S Department of Architecture, Design & Media Technology Mobilities and Urban Studies Rendsburggade 14 9000 Aalborg https://www.create.aau.dk/ Title Abstract: The Role of Pedestrian Safety in the This thesis is an investigation of to Municipal Traffic Safety Planning which extent 18 of the biggest municipal- ities in Denmark focus on pedestrians Subtitle in their traffic safety planning, both in When Maintenance Becomes Safety terms of pedestrian accidents in general Project and solo accidents. This is primarily Master thesis, 4th semester investigated through the study of the 18 municipalities’ traffic safety plans, Project duration as well as possible pedestrian strategies. February 2021 – May 2021 However, interviews have likewise been used, since this method makes it possi- Authors ble to ask clarifying questions and ac- Camilla Lønne Nielsen quire knowledge that might not have Sara Merete Kjeldbjerg Jensen been possible to get by reading. The definition of a traffic accident does not Supervisor include solo accidents with pedestrians, Harry Lahrmann why these are not currently included in the official statistics, which the munici- Co-supervisor palities base their traffic safety plans on. Claus Lassen For this reason, there is not much focus on solo accidents with pedestrians, and to a low extent on other pedestrian ac- cidents. It has become clear that pedes- trian safety, when talking about solo accidents, to a great extent is a matter Circulation: 2 of the daily maintenance, therefore we Total pages: 80 recommend e.g. -

Lister Til Hjemmesiden.Xlsx
FondUddelingsområde Projekttitel Organisation Afdelling Ansøger Beløb VILLUM FONDEN Børn, Unge og Science Makerspace i Byens Hus Gentofte Municipality Børn og Skole, Kultur, Unge og Fritid Anders-Peter Østergaard DKK 7.995.759,00 Science-camps på Amager Strand School Service Society Naturcenter Amager Strand Thomas Ziegler Larsen DKK 629.750,00 MakerKaravanen - et kørende fritidstilbud med fokus på science i samarbejde med lokalt erhvervsliv i Tønder Kommune Tønder Municipality Tønder Ungdomsskole Mikkel Brander DKK 153.519,00 Læring og viden gennem oplevelser The Danish Scout Association DDS Rougsø Gruppe Dag Kristiansen DKK 441.000,00 By-Rum-Laboratoriet i fritiden S/I Nørrebro Bispebjerg Klynge 4 Fritidscenter Bispebjerg Nord Thomas Budtz Graae DKK 2.966.900,00 Den Mørke Side Udfordring The Danish-French School SFO Joséphine Robert DKK 115.000,00 Science-klub med fokus på klima og bynatur Grundtvigsvej School SFO Nordlys og Klub Komenten Casper Gregers DKK 875.515,00 Science-aktiviteter og oplevelser - med et historisk afsæt The Green Guild Fonden Ulvsborg historiske værksted Mette Bohart DKK 500.000,00 Walk-in-tech - Åbent bemandet STEAM-laboratorium i Ungdomshuset Odense Youth House Odense The Clubhouse Karsten Damgaard DKK 389.521,00 Computational Empowerment: Emergerende teknologier i uddannelse Aarhus University Afdeling for Digital Design & Informationsvidenskab Ole Sejer Iversen DKK 10.071.272,00 Makerspace som læringslaboratorier Aalborg Municipality Skoleforvaltningen Rasmus Greve DKK 4.438.664,00 "Vores makersted" i Lejre -

Eco-Innovation in Denmark
Eco-innovation in Denmark EIO Country Profile 2016-2017 Eco-Innovation Observatory The Eco-Innovation Observatory functions as a platform for the structured collection and analysis of an extensive range of eco-innovation and circular economy information, gathered from across the European Union and key economic regions around the globe, providing a much-needed integrated information source on eco-innovation for companies and innovation service providers, as well as providing a solid decision-making basis for policy development. The Observatory approaches eco-innovation as a persuasive phenomenon present in all economic sectors and therefore relevant for all types of innovation, defining eco-innovation as: “Eco-innovation is any innovation that reduces the use of natural resources and decreases the release of harmful substances across the whole life-cycle”. To find out more, visit www.eco-innovation.eu and ec.europa.eu/environment/ecoap Any views or opinions expressed in this report are solely those of the authors and do not necessarily reflect the position of the European Commission. Eco-Innovation Observatory Country Profile 2016-2017: Denmark Author: Henry Varga Coordinator of the work package: Technopolis Group Belgium Acknowledgments The document has been prepared with the kind support of: Mr. Niels Henrik Mortensen (Danish Ministry of the Environment - Danish EPA), Ms. Signe Kromann-Rasmussen (Danish Ministry of the Environment - Danish EPA), Mrs. Hanne Juel (Central Denmark Region/ Midtjylland), Mr. Morten Christensen (Danish Regions), Mr. Christoffer Trojaborg Julian (State of Green) and Mr. Steffen Max Høgh (3R Kontor ApS). A note to Readers Any views or opinions expressed in this report are solely those of the authors and do not necessarily reflect the position of the European Union.