An Application of Geographically Weighted Regression to Agricultural Data for Small Area Estimates
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

GESTIONE ASSOCIATA VALUTAZIONE AMBIENTALE STRATEGICA Comuni Di Londa, Pelago, Pontassieve, Reggello, Rufina, San Godenzo
Via XXV Aprile, 10 - 50068 Rufina (Fi) Tel. 0558399623 Fax. 0558397245 E-mail: [email protected] Area Gestione difesa e uso del territorio GESTIONE ASSOCIATA VALUTAZIONE AMBIENTALE STRATEGICA Comuni di Londa, Pelago, Pontassieve, Reggello, Rufina, San Godenzo Rufina, 3 luglio 2018 Protocollo assegnato in via informatica Oggetto: procedimento di verifica di assoggettabilità a VAS relativo alla Variante n. 5 al Regolamento Urbanistico approvato con Deliberazione C.C. n. 7 dell’08.04.2014 per modifiche all’art. 62 – Area di recupero “Altomena” - delle N.T.A., in Comune di Pelago: esito istruttoria. IL RESPONSABILE AREA GESTIONE DIFESA E USO DEL TERRITORIO Richiamati: • il D. lgs. 152/2006 e ss.mm.ii.; • la L.R. 10/2010 e ss.mm.ii.; • lo Statuto dell’Unione di Comuni Valdarno e Valdisieve, approvato con Delibera C.U. n. 2 del 23 febbraio 2018; • il Regolamento del Servizio Associato VAS dell'Unione di Comuni Valdarno e Valdisieve approvato con Delib. di Giunta U.C.V.V. n. 53 del 20.05.2014; • Il Decreto del Presidente del’Unione di Comuni Valdarno e Valdisieve n. 9 del 28.08.2014 Comune di Pelago Prot. N. 8503 del 03-07-2018, Tipo: arrivo, Codici di Archivio: Unione Comune Valdarno e Valdisieve - Prot. partenza n. 10423 del 03-07-2018 di attivazione dell’Ufficio Associato VAS; Considerato che - in data 08.05.2018 sono state presentate dal Comune di Pelago in qualità di Autorità procedente e recepite al protocollo dell'Ente con i nn. 6358/57 e 6359/57 le note di avvio del procedimento ai sensi dell’art. -

Tuscany Flavors
Admire land of gently rolling hills, olives groves, wheat fields, vineyards, Discover flavors of Tuscany - land of undulating landscape, cypresses trees and idyllic estates, and be impressed by incredible treasures rich history and countless art jewels of art and culture in Florence, Siena, Montalcino and other places. 1. DAY Chianti Hills - Montaione After landing in Florence, we enter directly into the hilly landscape of Tuscany and after a short drive we reach our idyllic hotel near Montaione , a quiet little town with a delightfully maintained centre. The rest of the day is free for you to get acquainted with the resort. 2. DAY Highlights of Florence Today we will visit Florence, residence of Medici family during medieval time, to discover its countless treasures such as the Basilica Santa Maria Novella, Complex of Santa Maria del Fiore, Piazza del Duomo, the cathedral Santa Maria del Fiore, the Baptistry of San Giovanni, and Giotto's bell tower. Later drive up the other side of the River Arno to Piazzale Michelangelo to admire Florence magical skyline from above. The church of San Miniato al Monte is just a few steps further up the square. A leisurely stroll through the park down to the Flight trip – price incl. local transport Arno and back to the hotel ends the day. Price from 1.689€ 3. DAY Chianti - wine tasting in Castello di Meleto You enter the heart of the wine region and start a walk in Greve in GENERAL INFO Chianti. Time and time again, beautiful photographs are on your display. In the midst of this fantastic landscape, we reach Castello di ACCOMMODATION EXAMPLES Volpaia, which dates back to the early Middle Ages. -

Posti INFANZIA
SCUOLA DELL'INFANZIA - DISPONIBILITA' SUPPLENZE GPS A.S. 2021/22 Tipo di Posti al Posti al Ore Sede Denominazione Scuola Comune posto 31/8 30/6 Residue FIEE260008 DD Fucecchio FUCECCHIO AN 2 10 FIEE260008 DD Fucecchio FUCECCHIO EH 4 FIIC80800B IC Marradi MARRADI AN 1 FIIC80800B IC Marradi MARRADI EH 13 GAMBASSI FIIC809007 Ic Gambassi Terme AN 12 TERME GAMBASSI FIIC809007 Ic Gambassi Terme EH 2 13 TERME CAPRAIA E FIIC81000B IC Capraia e Limite AN LIMITE CAPRAIA E FIIC81000B IC Capraia e Limite EH 1 LIMITE MONTELUPO FIIC811007 IC Montelupo Fiorentino AN 1 FIORENTINO MONTELUPO FIIC811007 IC Montelupo Fiorentino EH 13 FIORENTINO FIIC812003 IC Gandhi FIRENZE AN 2 FIIC812003 IC Gandhi FIRENZE EH 2 12 FIIC81300V IC Amerigo Vespucci FIRENZE AN 1 FIIC81300V IC Amerigo Vespucci FIRENZE EH 5 13 FIIC81400P IC Dicomano DICOMANO AN FIIC81400P IC Dicomano DICOMANO EH 1 FIIC81500E IC Vicchio VICCHIO AN 1 FIIC81500E IC Vicchio VICCHIO EH 1 2 FIIC81500E IC Vicchio VICCHIO HN 1 FIIC81600A IC Firenzuola FIRENZUOLA AN 3 FIIC81600A IC Firenzuola FIRENZUOLA EH 1 1 MONTESPERTOL FIIC817006 IC Montespertoli AN I MONTESPERTOL FIIC817006 IC Montespertoli EH 1 I BARBERINO DI FIIC818002 IC Barberino Di Mugello AN 1 MUGELLO BARBERINO DI FIIC818002 IC Barberino Di Mugello EH 1 2 MUGELLO BARBERINO FIIC81900T IC Tavarnelle AN 1 TAVARNELLE BARBERINO FIIC81900T IC Tavarnelle EH 2 1 12 TAVARNELLE FIIC820002 IC Fiesole FIESOLE AN 2 FIIC820002 IC Fiesole FIESOLE EH 1 2 FIIC82100T IC Campi - Giorgio La Pira CAMPI BISENZIO AN 1 FIIC82100T IC Campi - Giorgio La Pira CAMPI BISENZIO -

Fiee000ve8 Provincia Di Firenze Fiee010ze9 Distretto
FIEE000VE8 PROVINCIA DI FIRENZE FIEE010ZE9 DISTRETTO 010 FICT703005 CENTRO TERRITORIALE PERMANENTE - ISTRUZIONE IN ETA' ADULTA CAMPI BISENZIO - VIA BUOZZI,65 (NON ESPRIMIBILE DAL PERSONALE DIRIGENTE SCOLASTICO) CON SEDE AMMINISTRATIVA IN CAMPI BISENZIO : FIIC86400Q DISTRETTI DI COMPETENZA : 010 FIEEB406G5 COMUNE DI CALENZANO FIEE827031 "ANNA FRANK" (ASSOC. I. C. FIIC82700R) VIA GIOVANNI XXIII,78 FRAZ. SETTIMELLO FIEE82702X "CONCETTO MARCHESI" (ASSOC. I. C. FIIC82700R) VIA DI CARRAIA FRAZ. CARRAIA FIEE82701V "DON LORENZO MILANI" (ASSOC. I. C. FIIC82700R) VIA DEL MOLINO N. 2 CALENZANO (SEDE DI ORGANICO - ESPRIMIBILE DAL PERSONALE DOCENTE) FIIC82700R ISTITUTO COMPRENSIVO CALENZANO CALENZANO - VIA MASCAGNI 15 (ESPRIMIBILE DAL PERSONALE A.T.A. E DIRIGENTE SCOLASTICO) CON SEZIONI ASSOCIATE : FIAA82700L - CALENZANO, FIAA82701N - CALENZANO, FIAA82702P - CALENZANO, FIAA82703Q - CALENZANO, FIAA82704R - CALENZANO, FIAA82705T - CALENZANO, FIEE82701V - CALENZANO, FIEE82702X - CALENZANO, FIEE827031 - CALENZANO, FIMM82701T - CALENZANO FIEEB507G0 COMUNE DI CAMPI BISENZIO FIEE821032 "DON MILANI" (ASSOC. I. C. FIIC82100T) VIA FONDI - S. PIERO A PONTI FRAZ. SAN PIERO A PONTI FIEE86401T AURORA GELLI (ASSOC. I. C. FIIC86400Q) VIA DI MEZZO CAMPI BISENZIO (SEDE DI ORGANICO - ESPRIMIBILE DAL PERSONALE DOCENTE) FIEE86403X CAPALLE "E. SALGARI" (ASSOC. I. C. FIIC86400Q) VIA DEI CONFINI FRAZ. CAPALLE FIEE86502P FRA' RISTORO (ASSOC. I. C. FIIC86500G) VIA PRUNAIA CAMPI BISENZIO (SEDE DI ORGANICO - ESPRIMIBILE DAL PERSONALE DOCENTE) FIEE86501N L. IL MAGNIFICO (ASSOC. I. C. FIIC86500G) VIA OMBRONE CAMPI BISENZIO FIEE86402V LA VILLA-PABLO NERUDA (ASSOC. I. C. FIIC86400Q) VIA DI VILLA FRAZ. LA VILLA FIEE82101X MARCO POLO (ASSOC. I. C. FIIC82100T) VIA PISTOIESE FRAZ. S. ANGELO A LECORE FIEE821021 VAMBA (ASSOC. I. C. FIIC82100T) VIUZZO DELLA COSTITUZIONE FRAZ. SAN DONNINO (SEDE DI ORGANICO - ESPRIMIBILE DAL PERSONALE DOCENTE) FIIC82100T ISTITUTO COMPRENSIVO GIORGIO LA PIRA SAN DONNINO - VIUZZO DELLA COSTITUZIONE (ESPRIMIBILE DAL PERSONALE A.T.A. -

Descrizione Comune Cognome Nome Selvaggina Minuta Greve in Chianti MAZZONI CARLO Selvaggina Minuta AZZERBONI ROBERTO Selvaggina
descrizione comune Cognome Nome selvaggina minuta greve in chianti MAZZONI CARLO Selvaggina minuta vicchio di mugello AZZERBONI ROBERTO selvaggina minuta marradi CARLONI VINCENZO Selvaggina minuta borgo san lorenzo MARTINI MASSIMO Selvaggina minuta firenzuola POZZI CARLO Colombaccio firenzuola BERNONI SERGIO Selvaggina minuta firenzuola GUARDUCCI STEFANO Colombaccio scarperia TENDI CARLO selvaggina minuta fiesole BARDI VITOSERGIO Selvaggina minuta marradi VISANI GERARDO Selvaggina minuta impruneta RONCHI ROMANO Selvaggina minuta reggello CAPANNI VALTERIO selvaggina minuta lastra a signa BENCINI ANNALISA Selvaggina minuta palazzuolo sul senio CANTAGALLI ORLANDO selvaggina minuta campi bisenzio MANETTI CLAUDIO Selvaggina minuta (1) firenzuola PETRI ALFREDO Selvaggina minuta (2) firenzuola PETRI ALFREDO selvaggina minuta vicchio di mugello GIOVANNINI FABRIZIO selvaggina minuta firenzuola FIORENTINI ITALO Selvaggina minuta firenzuola MONGARDI ORLANDO selvaggina minuta reggello ARNETOLI GRAZIANO selvaggina minuta vicchio di mugello BERTACCINI SILVANO 1\\\\\\\\\\\\\\\\\\\\\\LuogoNascita SpecieToponimo NomeToponimo NumeroCivicoCAP 19-feb-43 Greve in Chianti VIA SANMINIATELLI 10 50022 22 Dic.1938 Borgo San Lorenzo VIA DI MUCCIANO 25 50032 30 ago.1935 Marradi VIA PROVINCIALE 21 50034 01 apr.1971 Borgo San Lorenzo VIA RABATTA 56 50032 13 apr.1954 Riolo Terme VIA FIRENZE 75 48025 26mar.1954 Borgo San Lorenzo VIA DEL MONTELLO 2 50032 15 lug.1949 Prato VIA S.ANDREA A TONTOLI 8 59100 10mar.1970 Borgo San Lorenzo VIA DELL'AZZURRO 22 50038 08 mag.1948 Verghereto VIA V.EMANUELE 54 50134 11.sett.1928 Marradi VIA S.BENEDETTO 19 50034 10 sett.1937 Firenze VIA DELLE FONTI 9 50012 1. febb.1953 Incisa in Val d'Arno VIA SAMBUCHI 171 50066 29 ago.1971 Firenze VIALE A.VOLTA 40 50131 29 ago.1937 casola valsenio VIA REP.VALDOSSAOLA 24 48025 03 mag.1951 Campi Bisenzio VIA PISTOIESE 327 50058 12febb.1964 Pistoia VIA DI LUPICCIANO 29 51100 12 febb.1964 Pistoia VIA DI LUPICCIANO 29 5100 18 febb. -
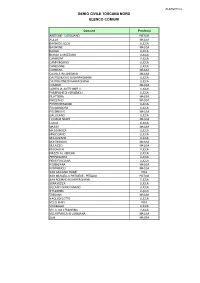
Allegato C Genio Civile Toscana Nord Elenco Comuni
ALLEGATO C GENIO CIVILE TOSCANA NORD ELENCO COMUNI Comune Provincia ABETONE - CUTIGLIANO PISTOIA AULLA MASSA BAGNI DI LUCCA LUCCA BAGNONE MASSA BARGA LUCCA BORGO A MOZZANO LUCCA CAMAIORE LUCCA CAMPORGIANO LUCCA CAREGGINE LUCCA CARRARA MASSA CASOLA IN LUNIGIANA MASSA CASTELNUOVO DI GARFAGNANA LUCCA CASTIGLIONE DI GARFAGNANA LUCCA COMANO MASSA COREGLIA ANTELMINELLI LUCCA FABBRICHE DI VERGEMOLI LUCCA FILATTIERA MASSA FIVIZZANO MASSA FORTE DEI MARMI LUCCA FOSCIANDORA LUCCA FOSDINOVO MASSA GALLICANO LUCCA LICCIANA NARDI MASSA LUCCA LUCCA MASSA MASSA MASSAROSA LUCCA MINUCCIANO LUCCA MOLAZZANA LUCCA MONTIGNOSO MASSA MULAZZO MASSA PESCAGLIA LUCCA PIAZZA AL SERCHIO LUCCA PIETRASANTA LUCCA PIEVE FOSCIANA LUCCA PODENZANA MASSA PONTREMOLI MASSA SAN GIULIANO TERME PISA SAN MARCELLO PISTOIESE - PITEGLIO PISTOIA SAN ROMANO IN GARFAGNANA LUCCA SERAVEZZA LUCCA SILLANO GIUNCUGNANO LUCCA STAZZEMA LUCCA TRESANA MASSA VAGLI DI SOTTO LUCCA VECCHIANO PISA VIAREGGIO LUCCA VILLA COLLEMANDINA LUCCA VILLAFRANCA IN LUNIGIANA MASSA ZERI MASSA ALLEGATO C GENIO CIVILE VALDARNO SUPERIORE ELENCO COMUNI Comune Provincia ANGHIARI AREZZO AREZZO AREZZO BADIA TEDALDA AREZZO BAGNO A RIPOLI FIRENZE BARBERINO DI MUGELLO FIRENZE BIBBIENA AREZZO BORGO SAN LORENZO FIRENZE BUCINE AREZZO CAPOLONA -CASTIGLION FIBOCCHI AREZZO CAPRESE MICHELANGELO AREZZO CASTEL FOCOGNANO AREZZO CASTEL SAN NICCOLO' AREZZO CASTELFRANCO - PIANDISCO' AREZZO CASTIGLION FIORENTINO AREZZO CAVRIGLIA AREZZO CHITIGNANO AREZZO CHIUSI DELLA VERNA AREZZO CIVITELLA IN VAL DI CHIANA AREZZO CORTONA AREZZO DICOMANO -

Empoli Castelfiorentino Certaldo Gambassi Terme
Stampato ORA 33 I 31 Orario invernale in vigore dal 16 settembre 2019 al 10 giugno 2020 Revisione 01/2019 Il servizio è sospeso nei seguenti giorni: 25 dicembre, 1 gennaio, Pasqua e 1 maggio Corse esercite da BUSITALIA I giorni di scuola sono quelli previsti della delibera RT nr. 288 del 27/03/2017 EMPOLI ● CASTELFIORENTINO ● CERTALDO ● GAMBASSI TERME ● MONTAIONE Lunedì - Sabato L-S 6 L-S L L-NS 6 L 6 L 6 L-S-F-& EMPOLI Via Bonistallo 13:05 13:55 EMPOLI Autostazione 07:12 07:35 07:40 07:50 08:40 08:40 10:00 11:00 12:28 13:05 13:07 : EMPOLI Piazza della Vittoria 07:13 07:36 07:41 07:51 08:41 08:41 10:01 11:01 12:30 : 13:10 : EMPOLI Via Sanzio : : : : : : : : 12:25 13:10 : 13:56 PONTE A ELSA 07:22 07:45 07:50 08:00 08:50 08:50 10:10 11:10 12:40 13:15 13:25 14:10 CASTELFIORENITNO Duca d'Aosta : 08:05 08:10 08:20 : : : : : : : CASTELFIORENTINO 06:45 07:42 08:00 08:10 08:15 08:25 08:25 08:30 09:10 09:10 09:25 10:30 10:30 10:35 11:30 12:05 13:00 13:15 13:40 13:40 CASTELFIORENTINO Duca d'Aosta : : : : : : : : : : 13:05 : : PETRAZZI : 07:47 : : 08:38 : 10:38 : 11:35 : : : : CERTALDO : 07:10 07:57 : : 08:45 : 10:45 : 11:45 : : : : VARNA 06:55 : : : : 10:45 12:15 : 13:25 : PILLO : : 08:10 08:35 09:35 : : 13:15 : 13:50 GAMBASSI TERME 07:05 07:30 08:20 08:45 09:45 10:55 12:25 13:20 13:35 14:10 MONTAIONE 07:15 08:30 08:50 09:55 11:05 12:35 13:40 13:45 14:20 6-S L-S L-S 6 L L 6 L L L L & EMPOLI Via Bonistallo 14:05 EMPOLI Autostazione 14:07 15:20 17:00 18:20 19:35 20:10 EMPOLI Piazza della Vittoria 14:10 15:21 17:01 18:21 19:36 20:11 EMPOLI Via Sanzio -

Incontri Metropolitani
Incontri Metropolitani Città Metropolitana di Firenze Report: I risultati emersi dagli incontri PREMESSA l presente documento costituisce la sintesi Il testo seguente si articola in due diverse I dei principali risultati emersi durante i sezioni: cinque Incontri Metropolitani realizzati nei diversi ambiti territoriali della Città Metropolitana e • una prima che descrive la metodologia in cui si è svolto l’evento e i comuni che vi ha preso dedicati ad un confronto collettivo con i Sindaci parte; e i dirigenti degli uffici tecnici comunali. L’attività di ascolto svolta è parte integrante del • una seconda che illustra le questioni processo partecipativo Upda0ng Piano, avviato sollevate dalla discussione, suddivise per aree territoriali. dalla Città Metropolitana per accompagnare in INDICE maniera partecipata e condivisa l’aggiornamento e il monitoraggio del Piano Strategico Metropolitano (PSM), dopo i tre anni L’evento…….….….….….….….….….….….…….… 3 dalla sua approvazione. Principali questioni emerse.….….…….… 7 Area Mugello.….….…..…..…..…..…..……..… 9 Area Fiorentina.….….….….…..…..…..……… 13 Area Valdarno Fiorentino e Valdisieve.… 19 Area Chianti Fiorentino.….….….….….….… 23 Area Valdarno Empolese e Valdelsa.……. 25 L’EVENTO L’evento “Incontri Metropolitani" è un incontro pubblico rivolto ai Sindaci del Nello specifico la discussione è stata avviata dalla definizione di due precise territorio metropolitano (o ai loro delegati) e ai Dirigenti degli Uffici tecnici comunali, domande: previsto per ognuno dei 5 ambiti territoriali della Città Metropolitana -

Castello Di Cabbiavoli the Puccioni Family Is Pleased to Welcome You in Cabbiavoli and Wish You a Pleasant Stay! Please Treat Our Home As Your Home
Castello di Cabbiavoli The Puccioni family is pleased to Welcome you in Cabbiavoli and wish you a pleasant stay! Please treat our Home as your Home Article published by the Magazine Italy - June 2005 ‘Cabbiavoli Castle - a Tuscan paradise’ by Adam Butler Situated prominently on a Tuscan hilltop amidst the rolling, vine and olive tree strewn hills around the town of Castelfiorentino lies the astonishingly beautiful Cabbiavoli Castle. This typically grand, Florentine-style residential complex comprises of a main building with a Baroque-façade where the living quarters are located, flanked by a tall medieval brick tower on one side and a little chapel dating to the 13th century on the other. Originally built in 1210 by a certain Count Alberti di Certaldo who was chief of the ruling Longobard family that dominated the nearby Elsa valley, the castle of Cabbiavoli was originally a fortified “borgo” of the Alberti family and in fact it still retained its farm and granary until the renovations in the late 1940s. The only parts remaining of the original fortified castle and the adjacent buildings are the surrounding defensive walls and the tower. This brick tower still stands proudly today (albeit slightly leaning) and, flanked by a huge ancient pine tree, offers dramatic views of the undulating, fertile countryside below, as far as the towered town of San Gimignano which is just visible on the horizon to the south. The Alberti family owned and lived in the castle until the 17th century, after which it fell into the hands of the patrician Brandini family. In 1900 Alice Brandini married Cesare Puccioni, son of a local entrepreneur Luigi who by 1888 had founded a chemicals factory just north of the town of Castelfiorentino. -

Bibliografia Di Montaione E Gambassi Terme (Pdf)
Rino Salvestrini Bibliografia di Montaione e Gambassi Terme 2 Premessa Questa bibliografia comprende tutto ciò che ho trovato su Montaione e Gambassi Terme, intesi anche con le loro frazioni, comprese quelle che ora non lo sono più e fanno parte di altre municipalità: Castelfiorentino (Castelnuovo in Valdelsa, Meleto, Mellicciano e Coiano); San Miniato (Canneto e San Quintino); Peccioli (Cedri); San Gimignano (Larniano, Pulicciano e Canonica); Volterra (La Nera). Di solito le bibliografie si dividono per Comune, ma in questo caso ho creduto giusto fare un lavoro unico, perché in un certo periodo i due Comuni ne formavano uno solo, comunque poi facendo parte della stessa zona (Valdelsa Fiorentina) e della medesima Diocesi (Volterra), certi libri vanno bene per l'uno e per l'altro Comune. L’elenco, che supera i mille titoli, forse non è completo e, ancora forse, certi lavori non sono necessari per una bibliografia essenziale, ma ho cercato di mettere tutto, poi qui ho fatto una selezione significativa. Certamente c'è ancora da ricercare, e soprattutto da aggiornare, perché nuovi studi via via escono continuamente, per fortuna! Fanno la parte del leone, per numero di scritti, San Vivaldo, la mineralogia di Iano e Montignoso, il Filicaia, la Pieve di Santa Maria a Chianni, il vetro, il Cieco da Gambassi e, di recente, l’agriturismo. Come è naturale, abbondano i saggi pubblicati sulla rivista MSV. A certi libri e saggi ho aggiunto, fra parentesi quadre, alcuni dati esplicativi. Ho riportato anche gli inediti, fra i quali una ventina di tesi di laurea. Montaione 31 dicembre 2010 Abbreviazioni MSV = Miscellanea Storica della Valdelsa. -

Ordinary Spaces and Public Life in the City of Fragments Spazi Ordinari E Vita Pubblica Nella Città Di Frammenti
FLORE Repository istituzionale dell'Università degli Studi di Firenze Ordinary Spaces and Public Life in the City of Fragments Questa è la Versione finale referata (Post print/Accepted manuscript) della seguente pubblicazione: Original Citation: Ordinary Spaces and Public Life in the City of Fragments / Giulio Giovannoni. - In: IN BO. - ISSN 2036-1602. - ELETTRONICO. - (2013), pp. 227-248. Availability: This version is available at: 2158/827298 since: Terms of use: Open Access La pubblicazione è resa disponibile sotto le norme e i termini della licenza di deposito, secondo quanto stabilito dalla Policy per l'accesso aperto dell'Università degli Studi di Firenze (https://www.sba.unifi.it/upload/policy-oa-2016-1.pdf) Publisher copyright claim: (Article begins on next page) 27 September 2021 Ricerche e progetti per il territorio, THE PUBLIC SPACE OF EDUCATION la città e l’architettura SPECIAL ISSUE #1/2013 Giulio Giovannoni Tenured researcher at the University of Florence in Urban Planning and Design, former Research Fellow in Urban Studies at the Johns’ Hopkins University. He has been a visiting scholar at UCBerkeley and at Harvard GSD. His current research focuses on suburbs, with a particular interest in international comparisons. Ordinary Spaces and Public Life in the City of Fragments Spazi ordinari e vita pubblica nella città di frammenti The Urban Design Studio held in the fall 2012 within the International Curriculum in Architectural Design at the University of Florence coped with the design of peripheries. These are the least-known parts of Florence but are still the places where most of people live. Here the traditional ideas of the city and of public spaces collapse. -

Enoproject Srl Consulenza Viticola Enologica Franco Bernabei Matteo Bernabei Viale Vittorio Veneto, 66 50022 Greve in Chianti (F
Enoproject Srl Consulenza Viticola Enologica Franco Bernabei Matteo Bernabei Viale Vittorio Veneto, 66 50022 Greve in Chianti (FI) Telefono 055853693 – 055853831 Email: Franco Bernabei: [email protected] Matteo Bernabei: [email protected] ENOPROJECT S.R.L. – A SOCIO UNICO – VIALE VITTORIO VENETO, 66 – 50022 – GREVE IN CHIANTI (FI) –TEL.055–853693/853831– FAX 055–8544472– E-MAIL: [email protected] –C.F./P.IVA 02578790285 SEDE LEGALE: VIALE DELLE TERME, 123 – 35031 ABANO TERME (PD) – TRIBUNALE PADOVA – N. 16495 REG. ORD. – N. 43086 SOC. – N. 48374 VOL. – C.C.I.A.A . RD . PD. N. 245776 CAP. SOC. EURO 10400,00 ENOPROJECT S.R.L. Franco Bernabei Making wine vineyard to vineyard, winery to winery: so one can follow the productive history of each winery. The many trips to France with visits to both small wineries to major Château had made it clear to Franco Bernabei the importance of “terroir” and how to grow the vines. Freelance wine maker since 1978 and then in 1993 Franco Bernabei and his wife Daniela founded ENOPROJECT, a wine making consulting company based in Greve in Chianti. Currently there are about thirty Italian wineries under the Enoproject wing. Ten people are currently working in Enoproject, amongst them his son Matteo, a graduate in Viticulture and Enology. His wife Daniela follows the administration and coordination of the office. 2 ENOPROJECT S.R.L. – A SOCIO UNICO – VIALE VITTORIO VENETO, 66 – 50022 – GREVE IN CHIANTI (FI) –TEL.055–853693/853831– FAX 055–8544472– E-MAIL: [email protected] –C.F./P.IVA 02578790285 SEDE LEGALE: VIALE DELLE TERME, 123 – 35031 ABANO TERME (PD) – TRIBUNALE PADOVA – N.